
- •Аннотация
- •От автора
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •1. СИСТЕМЫ И ПРОЦЕССЫ
- •2. ПОРЯДОК, НЕПОРЯДОК, БЕСПОРЯДОК И ХАОС
- •3. ТЕРМОДИНАМИКА
- •3.1 Начала термодинамики
- •3.2 Равновесная термодинамика
- •4. НЕРАВНОВЕСНАЯ ТЕРМОДИНАМИКА
- •4.1 Диссипативные структуры, системы и среды
- •4.2 Термодинамика необратимых процессов
- •4.3 Линейная неравновесная термодинамика
- •4.4 Нелинейная неравновесная термодинамика
- •4.5 Статистическая термодинамика
- •5. ЭНТРОПИЯ
- •5.1 Определение и свойства энтропии
- •5.2 Энтропия в химической термодинамике
- •5.3 Энтропия в статистической физике
- •5.3.1 Энтропия Больцмана-Планка
- •5.3.2 Энтропия Гиббса
- •5.4 Тсаллис (Цаллис) энтропия (Революция в термодинамике)
- •6. ГЕОМЕТРИЯ ФРАКТАЛОВ
- •6.1 Элементы геометрии фракталов
- •6.2 Размерности фракталов
- •6.3 Примеры фракталов
- •6.4 Фракталы и энтропия
- •7. ИНФОРМАТИКА
- •7.1 Информация, информатика и информационные технологии
- •7.2 Теория информации
- •7.2.1 Информация Хартли
- •7.2.2 Энтропия Шеннона
- •7.3 Отрицательная энтропия, антиэнтропия, экстропия
- •7.4 Алгоритмическая теория информации
- •7.4.1 Энтропия Колмогорова
- •7.4.2 Эпсилон-энтропия
- •7.5 Энтропия Кульбака-Лернера
- •7.6 Энтропия Реньи
- •7.7 Квантовая информатика
- •7.7.1 Некоторые положения квантовой механики
- •7.7.2 Энтропия фон Неймана
- •7.7.3 Линейная энтропия
- •7.7.4 Сравнение энтропий Реньи, Цаллиса и Неймана
- •7.7.5 Энтропия Холево
- •8. СИНЕРГЕТИКА
- •8.1 Синергизм и синергетика
- •8.2 Детерминизм, случайность и неопределённость
- •8.3 Простые и сложные системы
- •8.4 Анализ систем
- •8.5 Параметры порядка (управляющие параметры)
- •8.6 Процессы самоорганизации
- •9. СИСТЕМЫ И ЗАКОНЫ ИХ ЭВОЛЮЦИИ
- •9.1 Статические системы
- •9.2 Динамические системы
- •9.3 Линейные динамические системы
- •9.4 Нелинейные динамические системы
- •9.5 Эволюция динамической системы
- •9.6 Математическое описание эволюции динамической системы
- •10. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ОПИСАНИИ ДИНАМИЧЕСКИХ СИСТЕМ
- •10.1 Обыкновенные дифференциальные уравнения
- •10.2 Фазовое пространство и пространство состояний
- •10.3 Линейные ОДУ на плоскости
- •10.4 Нелинейные дифференциальные уравнения
- •11. ОТОБРАЖЕНИЯ
- •11.1 Системы с дискретным временем в отображениях
- •11.2 Итерации в исследовании динамических систем
- •11.3 Графические методы нахождения неподвижных точек и исследования их свойств
- •11.4 Многопараметрические отображения
- •11.5 Примеры некоторых важные отображений
- •12. ОСОБЫЕ ТОЧКИ ФАЗОВЫХ ПОРТРЕТОВ ДИНАМИЧЕСКИХ СИСТЕМ
- •12.1 Дифференциальные уравнения и особые точки
- •12.2 Классификация точек равновесия
- •12.3 Фазовые портреты и особые точки нелинейных ОДУ
- •12.4 Многомерные системы
- •13. РЕГУЛЯРНЫЕ АТТРАКТОРЫ И РЕПЕЛЛЕРЫ
- •13.1 Типы аттракторов
- •13.2 Фазовый объём
- •13.3 Репеллеры
- •13.4 Осциллятор и осцилляции
- •14. УСТОЙЧИВОСТЬ ДИНАМИЧЕСКИХ СИСТЕМ
- •14.1 Устойчивые и неустойчивые равновесия
- •14.2 Устойчивость по Ляпунову (метод первого приближения)
- •14.3 Показатель Ляпунова
- •14.4 Устойчивость нелинейной системы
- •14.5 Метод функций Ляпунова
- •14.6 Функция Ляпунова и энтропия
- •14.7 Асимптотическая устойчивость
- •14.8 Устойчивость особых точек
- •14.9 Устойчивость особых точек
- •14.10 Устойчивость решений дискретных уравнений
- •15. БИФУРКАЦИИ
- •15.1 Бифуркации: основные понятия и классификация
- •15.2 Элементы теории бифуркаций
- •15.3 Простейшие бифуркации
- •16. БИФУРКАЦИИ ЦИКЛОВ
- •16.1 Предельные циклы
- •16.2 Устойчивость предельных циклов
- •16.3 Бифуркации устойчивых предельных циклов
- •16.5 Бифуркация рождения пары устойчивых замкнутых траекторий.
- •16.6 Транскритическая (обмена устойчивостью между циклами) бифуркация.
- •16.7 Бифуркация исчезновения (рождения) пары замкнутых траекторий.
- •16.8 Бифуркация удвоения периода цикла
- •16.9 Бифуркация рождения (гибели) двумерного тора.
- •16.10 Гомоклиническая бифуркация рождения/исчезновения цикла
- •17. ДИНАМИЧЕСКИЙ ХАОС
- •17.1 Хаос статистический и динамический
- •17.2 Предсказание статического поведения системы
- •17.3 Сценарии перехода к хаосу
- •17.4 Примеры систем с хаосом
- •18. ХАОС В ЛИНЕЙНЫХ ОДНОМЕРНЫХ СИСТЕМАХ
- •18.1 Бифуркационные диаграммы
- •18.2 Лестница Ламерея
- •18.3 Отображение Бернулли
- •18.4 Треугольное отображение
- •18.5 Отображение «тент»
- •18.6 Канторов репеллер
- •18.7 Детерминированная диффузия
- •19. ХАОС В ЛОГИСТИЧЕСКОМ ОТОБРАЖЕНИИ
- •19.1 Переход к хаосу через удвоение периода
- •19.2 Логистическое уравнение
- •19.3 Дискретное логистическое уравнение
- •19.4 Логистическое отображение
- •19.5 Бифуркационная диаграмма логистического отображения
- •19.6 Цикл периода 3
- •19.7 Фазовые диаграммы логистического отображения
- •19.8 Аттракторы и фракталы в логистическом отображении
- •20. ХАОС В НЕЛИНЕЙНЫХ ОДНОМЕРНЫХ ОТОБРАЖЕНИЯХ
- •20.1 Отображение xn+1=С+xn2.
- •20.2 Отображение xn+1=а-xn2.
- •20.3 Подобие окон периодической динамики
- •20.4 Порядок Шарковского
- •20.5 Универсальность Фейгенбаума
- •20.6 Устойчивость циклов одномерных отображений
- •20.7 Топологическая энтропия
- •20.8 Синус-отображение
- •21. ХАОС В НЕЛИНЕЙНЫХ ДВУМЕРНЫХ ОТОБРАЖЕНИЯХ
- •21.1 Отображение Эно (Henon map)
- •21.2 Отображение подковы и отображение пекаря
- •21.3 Отображение «кот Арнольда» (Arnold’s cat map)
- •22. НЕРЕГУЛЯРНЫЕ АТТРАКТОРЫ
- •22.1 Хаос в консервативных и диссипативных системах
- •22.2 Регулярные и хаотические аттракторы
- •22.3 Квазиаттракторы
- •22.4 Хаотически аттракторы
- •22.5 Негиперболические хаотические аттракторы
- •22.6 Фрактальные аттракторы
- •22.7 Характеристика нерегулярных аттракторов
- •22.8 Странные нехаотические аттракторы
- •22.9 Сингулярные аттракторы
- •22.10 Многомерные нерегулярные аттракторы
- •22.11 Дикие аттракторы

http://profbeckman.narod.ru/
20. ХАОС В НЕЛИНЕЙНЫХ ОДНОМЕРНЫХ ОТОБРАЖЕНИЯХ
Выше было подробно описано логистическое отображение вида xn+1=r(xn-xn2), которое можно представить как xn+1=1- xn2. В данной главе мы продолжим рассмотрение одномерных квадратичных отображений на примере xn+1=С+xn2 и xn+1=a-xn2. Все квадратичные отображения имеют похожие свойства (каждое имеет хотя бы одну точку, в которой производная от функции обращается в нуль; способно к хаотическому движению, имеет самоподобную (фрактальную) структуру бифуркационной диаграммы, зависит от одного параметра и проявляет сингулярность) но есть и отличия.
Затем будут обсуждены некоторые другие нелинейные отображения: одномодальное синус отображение и бимодальное кубическое отображение.
20.1 Отображение xn+1=С+xn2.
Ранее мы уже рассмотрели свойства типичного представителя квадратичных отображений – логистического отображения xn+1=r(xn-xn2). Теперь обсудим поведение другого представителя семейства одномерных квадратичных отображений:
xn+1=С+xn2. |
(1) |
Покажем, что это простое отображение обладает нетривиальной и богатой динамикой. При изменения параметра C устойчивые периодические орбиты отображения испытывают каскады бифуркаций (что проявляется, например, в самоподобии множества Мандельброта).
Напомним, что точки, в которых производная f(1)(xc)=0 называются критическими точками. Для аналитического отображения известно, что каждый устойчивый цикл обязательно притягивает к себе критическую точку. Так как у квадратичного отображения есть единственная критическая точка xc=0, то у него может существовать только один притягивающий цикл и начинать его поиски следует из точки xc=0. Для функции f(x)=x2+С вторая итерация функции f(2) помимо существовавших ранее двух отталкивающих неподвижных точек добавляет пару притягивающих неподвижных точек, которые приводят к появлению цикла с периодом 2. При переходе С через значение -3/4 система претерпевает бифуркацию удвоения периода. Другая бифуркация удвоения периода возникает при С=-5/4. Когда С становится меньше этого значения, орбиты начинают притягиваться циклом с периодом 4. По мере того как С убывает, последовательно встречаются притягивающие периодические орбиты длины 8, 16 и т. д.
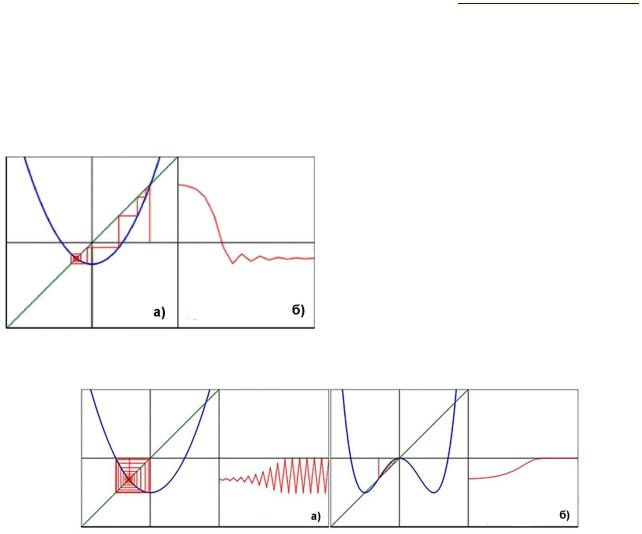
За динамикой одномерного вещественного отображения удобно следить по итерационной диаграмме (рис. 1). Синяя кривая это N-ая итерация отображение f oN(x) = f(f(...f(x))). Зеленая линяя y=x. Координаты изменяются в пределах -2≤x,y≤2. Т.к. f(0)=C, то при N=1 значение C совпадает с y(0). Зависимость xn от n строится в правом окне (итерации начинаются с x0). Чтобы построить итерационную диаграмму, проведем красную вертикальную линию из начальной точки xo=0 к синей линии y=f(x)=x2+С, где yo =f(xo). Чтобы получить следующую итерацию, строим горизонтальную линию к зеленой диагонали y=x, где x1=yo=f(xo). Далее снова строим вертикальную линию к синей кривой,
чтобы получить y1=f(x1) и т.д. Точки fc: xo→x1→x2→... при некотором значении С образуют орбиту точки xo.
Рис. 1. Итерационная диаграмма отображения xn+1=С+xn2: С=-1,35,
х0=0.
Рассмотрим теперь неподвижные точки отображения (1).
Неподвижные точки x•=f(x• ) отображения совпадают с пересечением y=x и y=f(x) (т.е. зелёной и синей кривых). У квадратичного отображения есть две неподвижные точки (возможно комплексные), определяемые квадратным уравнением f(x*)-x*=x*2+С-x*=0,
|
|
|
|
|
http://profbeckman.narod.ru/ |
|
x1,2=1/2 (1/4-С)½. |
Первая производная отображения в неподвижной точке m=f'(x* )=2x* |
|||||
называется |
|
|
или собственным значением) точки. Для малого δx |
|||
|
мультипликаторм ( 2 |
|
|
(2) |
||
f(x*+δx)=f(x*)+mδx+O(δx )≈x*+mδx. |
|
|
||||
Напомним, |
что |
неподвижная |
точка |
устойчивая |
(притягивающая), |
|
сверхустойчивая, неустойчивая или нейтральная в соответствии со значением мультипликатора |m|<1, |m|=0, |m|>1 или |m|=1, соответственно.
Вторая неподвижная точка (на рис. 2б) – всегда отталкивающая. При |x|> x2 итерации расходятся к бесконечности. При |x|<x2 они сходятся к притягивающей неподвижной точке x1. Точки этого интервала образуют её бассейн притяжения.
Рис. 2. Итерационная диаграмма отображения xn+1=С+xn2: С=-0,5, х0=1,35.
При C=-1 у отображения есть притягивающий цикл с периодом два (рис.
3б). У второй итерации отображения f o2 при этом появляются две притягивающие неподвижные точки.
Рис. 3. Итерационная диаграмма отображения xn+1=С+xn2: С=-1, х0=-0,6.
Рассмотрим теперь переход к хаосу путём удвоения периода.
Каскад бифуркаций (последовательность Фейгенбаума или сценарий удвоения периода) – один из типичных сценариев перехода от порядка к хаосу, от простого периодического режима к сложному апериодическому при бесконечном удвоении периода.
Последовательность Фейгенбаума имеет самоподобную, фрактальную структуру – увеличение какой-либо области выявляет подобие выделенного участка всей структуре. Анализ механизмов перехода от порядка к хаосу выявил универсальность относительно немногих сценариев перехода к хаосу. Вхождение системы в непредсказуемый режим описывается каскадом бифуркаций, следующих одна за другой. Каскад бифуркаций ведет последовательно к появлению выбора между двумя решениями, затем четырьмя и так далее, система начинает колебаться в хаотическом, турбулентном режиме последовательного удвоения количества возможных значений.
Применим показатели Ляпунова к исследованию устойчивости особых точек квадратического отображения. Для отображения xn+1=f(xn) малому отклонению δxo координаты точки xo соответствует малое изменение координаты x1 δx1=f'(xo) δxo. Для n-ой итерации отображения
δxn = δxo∏i=0,n-1 f '(xi ). (3)
Показатель Ляпунова для отображения выражается через это изменение по формуле Λ=limn → ∞ Ln, Ln=1/n log|δxn /δxo|=1/n ∑i=0,n-1 ln |f '(xi )|. У хаотической траектории
|δxn| растёт с увеличением n, поэтому для неё Λ>0. Для притягивающего цикла показатель
http://profbeckman.narod.ru/
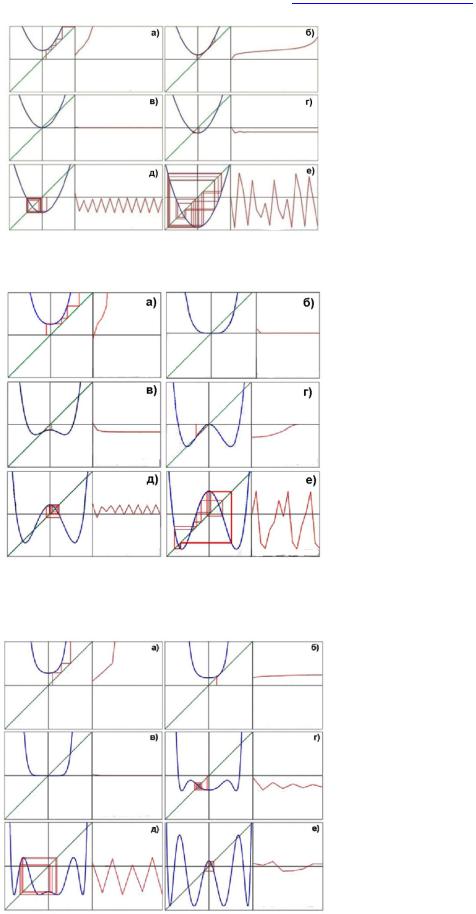
Рис. 4. Возникновение хаотических колебаний при опускании параболы: а – С=0,5122,
х0=0,2341; б – С=0,2683, х0=- 0,0488; в – С=0,0049, х0=0,039; г – С=-0,3073, х0=0,0683; д – С=-9,415, х0=0,2829; е – С=-1,8195, х0=0,085.
Рис. 5. Диаграммы второй итерации отображения (1): а – С=0,5681, х0=-0,1902; б -
С=-0,0051, х0=0,1871; в – С=-0,4713, х0=0,0721; г – С=-1, х0=-0,6; д – С=-1,3267, х0=0,5029; е – С=-1,6516, х0=-0,0852.
Рис. 6. Диаграммы третьей итерации отображения (1): а – С=0,3442, х0=0,1871; б – С=0,2507, х0=0,3626; в – С=-0,0066, х0=0,0585; г – С=-0,6967, х0=-0,0819; д – С=-1,3049, х0=0,1754; е – С=-1,7961, х0=0,14084.
http://profbeckman.narod.ru/
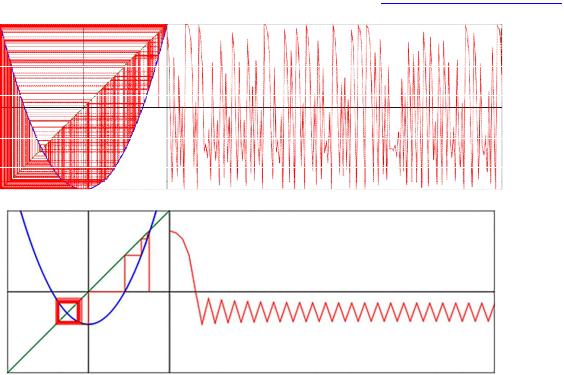
Рис. 7. Хаотическая траектория квадратичного отображения при С=-2
Рис. 8. Возникновение устойчивой орбиты при касательной бифуркации.
В точке С=1/4 парабола касается диагонали, а при С<1/4 они пересекаются в двух точках, соответствующих устойчивой и неустойчивой неподвижным точкам. Это явление называется касательной бифуркацией. Устойчивая орбита с периодом 3 также рождается в касательной бифуркации при С=-1.75 и далее, при уменьшении показателя Ляпунова L отрицательный. При С>1/4 итерации квадратичного отображения расходятся. параметра, повторяет весь каскад бифуркаций квадратичного отображения.
Рассмотрим бифуркации удвоения периода.
При С<-3/4 производная в левой неподвижной точке f'(x1)=m<-1 и точка теряет устойчивость. В окрестности С=-3/4, после первой итерации δx'=mδx~-δx меняет знак, а после второй итерации снова δx''=m2δx~δx. Поэтому у отображения появляется притягивающая периодическая орбита с периодом 2 x3→x4→x3 ... Это явление называется
бифуркацией удвоения периода.
У второй итерации квадратичного отображения f o2(x) при этом появляются две притягивающие неподвижные точки x3, x4 (соответствующие устойчивому циклу) и неустойчивая x1 (между ними). Отметим, что в окрестности нуля f o2(x) похожа на параболу и при дальнейшем уменьшении c также испытывает бифуркацию удвоения периода после которой у квадратичного отображения появляется устойчивый цикл с периодом 4 и т.д. То, что устойчивые орбиты с разными периодами испытывают подобные бифуркации, объясняется теорией перенормировок (renormalization theory). Заметим, что неустойчивые орбиты уже никогда больше не исчезают.
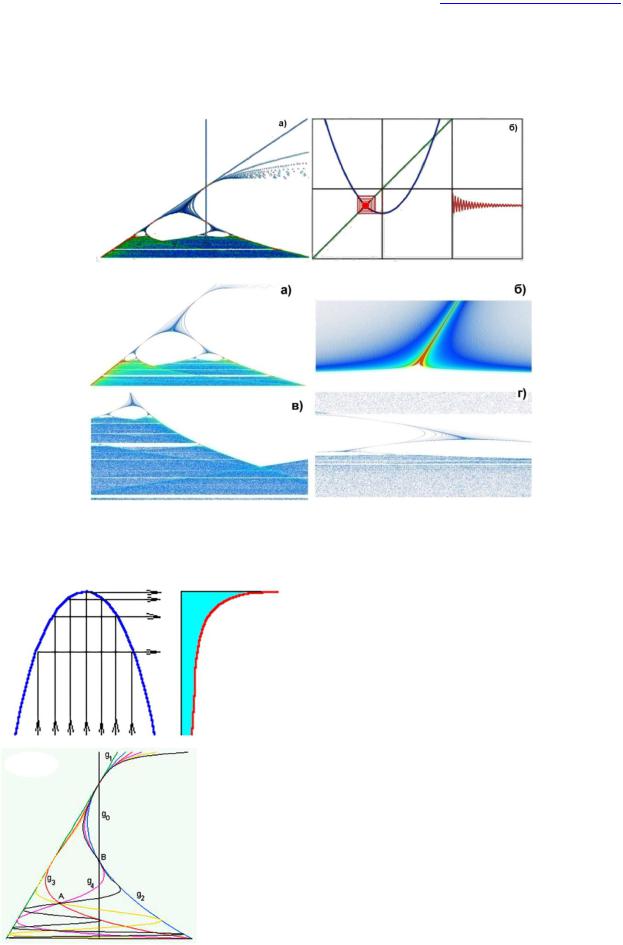
Рассмотрим теперь бифуркационную диаграмму (рис. 9а).
Будем строить итерации fc: x1=0→x2→x3→...→xMax для вещественных С на плоскости (x, С). Цвета (от синего к красному) показывают, как часто орбита попадает в данную точку (переходный процесс показывает, как быстро итерации сходятся). По итерационной диаграмма рис. 9б можно проследить за орбитой точки х=0 при соответствующем значении С.
Координаты центра изображения x,c и Δx,Δc отображаются в текстовом поле. Синяя вертикальная линия проходит через начальную точку x=0.
Верхняя часть диаграммы рис. 10 начинается с касательной бифуркации при C=1/4. При -3/4≤C≤1/4 существует единственная неподвижная притягивающая точка. В окрестности C=-3/4 видна точка ветвления бифуркации удвоения периода, после чего
http://profbeckman.narod.ru/
неподвижная точка теряет устойчивость и появляется притягивающая орбита с периодом 2. Далее после новой бифуркации удвоения периода возникает орбита с периодом 4 и т.д. Каскад бифуркаций удвоения периода заканчивается при С=-1.401 после чего возникает область хаотической динамики, которая заканчивается кризисом при C=-2. В области хаотической динамики видны узкие горизонтальные белые полосы окон
Рис. 9. Итерационная диаграмма отображения (1): С=-0,7, х0=0.
Рис. 10. Бифуркационная диаграмма отображения (1) в различных масштабах.
регулярной динамики. Самая большая полоса внизу соответствует окну с периодом 3.
В области изменения параметра r>3 наблюдается каскад удвоения периода. r>3,5699456... – поведение хаотическое, каскад удвоения периода заканчивается. Малые изменения начальных условий приводят к несопоставимым отличиям дальнейшего
поведения системы.
Можно найти каустики бифуркационной диаграммы.
Рис. 11. Построение распределения точек хаотических орбит.
. Рис. 11 поясняет, что каустики (см. далее) в распределении точек хаотических орбит генерируются экстремумами отображения. Поэтому
особенности (выделяемые красным цветом) на диаграмме
появляются на образах критической точки fc on(0). Обозначая gn(С)=fcon(0), получим go(С)=0, g1(С)=С,
g2(С)=С2+ С, ... Кривые g0,1,...,6(С) показаны на Fig. 12.
Рис. 12. Каустики отображения (1).
Отметим, что аттрактор квадратичного отображения заключен между кривыми g1(c) и g2(c). Точка пересечения каустики с вертикальной прямой x=0 на диаграмме соответствует окну периодической динамики.
