http://profbeckman.narod.ru/
орбиты для начального условия x0=0,4 и x0*=0,40001 и =0,9999; б – абсолютное расстояние между двумя орбитами.
18.6 Канторов репеллер
На рис. 34 показано, как классическое множество Кантора появляется в динамике отображения тент fc(x) при c=3. Легко убедиться, что при x>1 итерации уходят в -∞. Как видно из рисунка, на первой итерации отображения выпадает открытый интервал (1/3,2/3), а два интервала [0,1/3] и [2/3,1] линейно отображаются в [0,1]. Повторяя этот процесс до бесконечности, мы будем каждый раз вырезать центральную 1/3 из оставшихся на
предыдущем шаге интервалов (несколько первых шагов показаны на рисунке). В результате мы получим фрактальное множество Кантора. Суммарная длина вырезанных интервалов
1/3+2/9+4/27+...=1/3∑n=0,∞(2/3)n=1/3[1/(1-2/3)]=1,
т.о. мера Лебега (площадь) классического множества Кантора равна нулю. Его фрактальная размерность log2/log3. Множество Кантора с нулевой мерой появляется в отображении тент при любом c>2.
Рис. 31. Бифуркационная диаграмма отображения тент. Более высокая плотность соответствует более высокой вероятности, что переменная x примет данное значение для параметра . Зачернённые области – аттрактор хаотического движения.
Рис. 32. Увеличение рисунка в районе острия даёт более подробную информацию о бифуркационной диаграмме отображения тент ( макс=0.55).
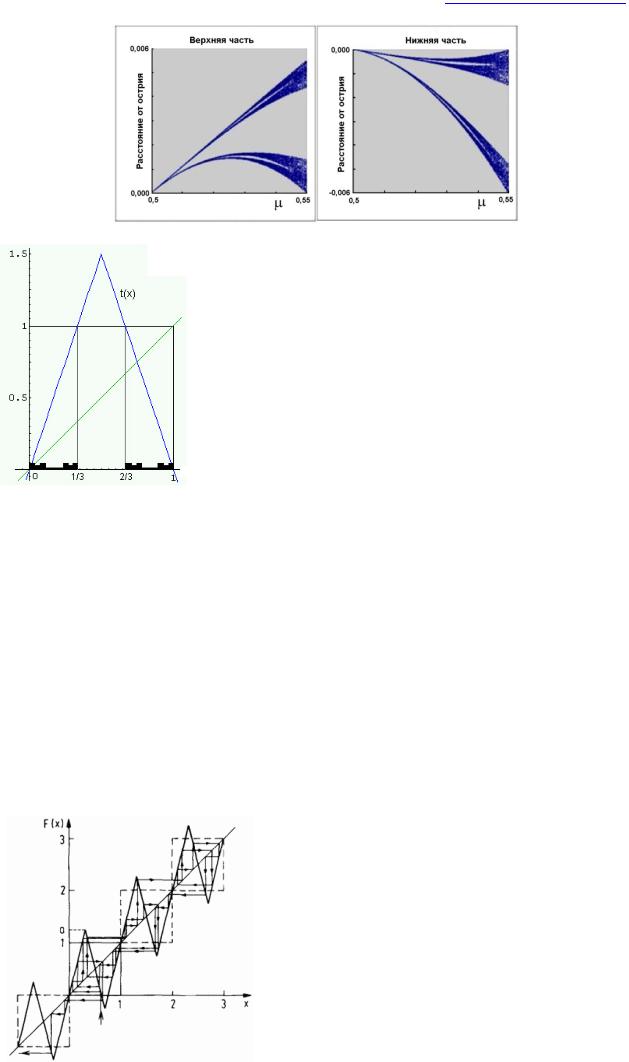
http://profbeckman.narod.ru/
Траектория медленно удаляется от начала координат (рис. 35). Диффузия возникает не за счёт случайных сил, как в броуновском движении, а за счёт движения внутри одного или нескольких единичных отрезков, система "забывает своё прошлое".
Вычислим <x2>. Координату точки траектории х представим в виде суммы номера отрезка N и положения y из отрезка [0, 1]:
x =N +y . |
(35) |
Для рассматриваемого отображения имеем |
|
N +1+y +1=F(N +y )=N +y +f(y ), |
(36) |
что эквивалентно паре динамических уравнений |
|
N +1-N =[y +f(y )]= (y ), |
(37a) |
y +1=y +f(y )-[y +f(y )]=g(y ), |
(37б) |
где [z] означает целую часть числа z. |
|
На рис. 36 показаны функция (y ) которая представляет собой величину скачка, описываемого целым числом, и функция g(y ) дающая остаток для координаты +1.
Расстояние от начала координат
t 1 |
t 1 |
|
|
Nt N 1 N |
y ; |
N0 1. |
(38) |
0 |
0 |
|
|
Рис. 36. Разложение кусочно-линейного отображения.
Усреднённый квадрат расстояния (дисперсия):
Для дисперсии имеем
t 1 |
|
Nt2 y y |
(39) |
,
Усреднение <...> берётся по всем начальным условиям y0. Для простоты полагаем, что <Nt> =0.
Если движение, задаваемое g(y) настолько хаотично, что корреляции между у
нет, т.е. < (y ), (y ) , .
|
Nt2 |
1 t 1 |
2 |
y |
|
dy y y . |
|
||
lim |
|
lim |
|
|
|
(40) |
|||
|
|
||||||||
t t |
t t |
0 |
|
|
|
|
|
||
Если g(y) имеет инвариантную плотность, удовлетворяющую уравнению
( ) |
= ∫ |
[ ( ) |
− |
] |
( ) |
(41) |
|
|
, |
тогда
<Nt2>=2Dt , для t>>1, т.е. <Nt2> растёт линейно со временем.
1
D1 dyp(y) 2 (y) - коэффициент диффузии. 2 0
Диффузия имеет место тогда, когда координаты y в достаточной степени не коррелированны; в этом случае двойная сумма в (39) сводится к обыкновенной. (Для вполне коррелированного движения <Nt2) пропорционально t2. Таким образом, для периодического отображения само наличие диффузии уже указывает на хаотичность движения, разрушающего корреляции внутри отрезков.
Для коэффициента диффузии существует простой масштабный закон, имеющий чисто геометрическую природу. Если интервалы , через которые траектории перескакивают из одного отрезка в другой, достаточно малы (так что изменением в этой
http://profbeckman.narod.ru/
области можно пренебречь (т. е. (x )= ), то, поскольку 2 принимает значение либо 0, либо 1, коэффициент диффузии
D 1 , 2
На рис. 37 показано, что D имеет скейлинг:
D (a-1)1/z,
когда отображение f(x) имеет максимум (и минимум) порядка z.
Рис. 37. Вариация порядка (a-1)1/z когда f(x) имеет максимум порядка z (схематично).