7.2.2 Энтропия Шеннона

http://profbeckman.narod.ru/

информационная энтропия, объяснив, что никто не понимает и никогда не поймёт, что такое энтропия, поэтому у Шеннона в спорах будет преимущество. Нейман оказался прав.

Энтропия Шеннона (информационная энтропия) – мера неопределённости (непредсказуемая информация), связанная со случайной величиной; степень неполноты, неопределённости знаний. Определяет количество информации (информационную ёмкость системы), содержавшейся в сообщении (в битах на символ); неопределённость появления какого-либо символа первичного алфавита, минимальная длина сообщения, необходимая для передачи информации; абсолютный предел наиболее возможного сжатия без потерь любого сообщения; мера среднего информационного содержания случайной величины, которое наблюдатель (получатель сообщения) теряет, когда ему неизвестно значение (исход) случайной величины. При отсутствии информационных потерь энтропия численно равна количеству информации на символ передаваемого сообщения. Если сигнал на выходе канала связи является точной копией сигнала на входе то энтропия отсутствует. Отсутствие шума означает максимум информации.

Информационная энтропия – мера неопределённости какого-либо опыта (испытания, сообщения источника, неопределённости вероятностного распределения), который может иметь различные исходы, а значит, и количество информации. Означает меру неупорядоченности (непредсказуемости) системы; чем меньше элементы системы подчинены какому-либо порядку, тем выше энтропия.

Пример: Неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь энтропия численно равна количеству информации на символ передаваемого сообщения.

Энтропия – макроскопическая величина. Она применима только для скоплений частиц, т.е. для термодинамической системы.

Энтропию понимают как недостающую информацию о системе, т.е. как степень нашей неосведомленности. Главную роль в способе описания энтропии играет число доступных микросостояний. Если в системе миллион состояний, и мы не знаем, в каком из них она находится, степень нашей неосведомленности намного больше, чем, если бы в ней было только десять состояний. Поэтому о системе с высокой энтропией известно намного меньше, чем о системе с низкой энтропией.

Информационная энтропия – мера хаотичности информации – связана с вероятностью появления тех или иных символов при передаче сообщений; это мера количества информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения; пропорциональна логарифму числа возможных эквивалентных сообщений. Она говорит о том, насколько тяжело делать предсказания о событиях описываемых вероятностным распределением. Чем больше энтропия, тем тяжелее делать предсказания. Энтропия – мера неопределенности некоторой ситуации, она возрастает по мере увеличения числа случайных ошибок при передаче сообщений; мера рассеяния, подобная дисперсии. Но если дисперсия является адекватной мерой рассеяния лишь для специальных распределений вероятностей случайных величин (например, для распределения Гаусса), то энтропия не зависит от типа распределения.

Если некий опыт имеет n равновероятных исходов, а другой опыт m равновероятных исходов, то составной опыт имеет nm таких исходов. При вводе меры неопределенности f требуется, чтобы, чтобы неопределенность росла с ростом числа возможных исходов, и неопределенность составного опыта была равна сумме неопределенности отдельных опытов, мера неопределенности должна быть аддитивной: f(nm)=f(n)+f(m). Такая мера неопределенности введена К. Шенноном:

N

H X р(Xi )log р Xi

где Х – дискретная случайная величина с диапазоном изменчивости N, р(Xi) – вероятность i -го уровня X.

http://profbeckman.narod.ru/

Величина энтропии заключена в пределах: 0 H(X) logN. Нижняя грань соответствует вырожденному распределению (неопределенность величин Х отсутствует, т.е. Xj=const). Верхняя грань соответствует равномерному распределению. Все N значений Xi встречаются с равной вероятностью. Здесь рассматривается не само событие, а информация о нём. Если состояние системы известно, то нет смысла передавать сообщение: оно не несёт информации. Сообщение приобретает смысл только, если состояние системы заранее неизвестно, обладает какой-то степенью неопределенности. Если некоторое значение бита очень вероятно, его информационное содержание низко; если значение маловероятно, бит несёт гораздо больше информации. Нужно найти сумму всех возможных значений и умножить на их вероятность, поскольку наиболее вероятные значения встречаются чаще.

Информационная энтропия обладает следующими свойствами:

1)Энтропия H(p1, p2,…,pn)=0 тогда и только тогда, когда все вероятности pi, кроме одной, равны нулю, а эта единственная вероятность равна единице. Это тот случай, когда о система все известно заранее и результат не дает новую информацию. H=0 только в случае полной определенности исхода опыта, при отсутствии неопределенности (опыты независимы). Во всех других случаях информация (энтропия) положительна; Информация опыта равна среднему значению количества информации, содержащейся в каком-либо одном его исходе.

2)При объединении независимых систем их энтропии складываются. Если A и B – два независимых случайных объекта с числом состояний n и m соответственно, то состояния системы образуются совместной реализацией объектов А и В). Тогда

находиться в состоянии (ai, bj).

Свойство аддитивности: количество энтропии не зависит от того, как система событий разделена на части (подсистемы). Например, энтропия n бросаний игральной кости в n раз больше, чем энтропия одного бросания.

3). Энтропия непрерывна: изменение значения одной из вероятностей на очень маленькую величину изменяет энтропию также на маленькую величину.

4) Энтропия (информация) симметрична относительно последовательности опытов:

Hn p1, p2 ,... Hn p2 , p1,... и т.д.

5) Энтропия максимальна, если все исходы одинаково вероятны (неопределённость является самой высокой, когда все возможные события равновероятны). При заданном n величина H максимальна и равна log2n, когда все pi равны между собой, то есть p1=p2=…=pn=1/n. Энтропия системы с равновозможными состояниями pi=1/n равна логарифму числа состояний n. Максимум энтропии соответствует наибольшей неопределённости или равенству вероятностей всех возможностей. Максимальное значение энтропии физической системы с конечным числом состояний равно логарифму числа состояний и достигается, когда все состояния равновероятны. Степень неопределённости опыта тем больше, чем больше число n его исходов.

(9)

Для равновероятных событий энтропия увеличивается с увеличением их числа:

информации. Максимальное разнообразие Hmax=log2n и справедливо oH Hmax

6) Если две произвольные системы А и В объединяются в одну, то энтропия сложной системы (А,В) равна

где H(A|B) - условная энтропия второй части В относительно первой. p(bj|ai) - условная вероятность того, что система А находится в состоянии bj при условии, что система А

находится в состоянии ai; по теореме умножения p(bj|ai)=pij/pi, pi=p(A ai). В случае любого числа объединяемых систем:

H(A1,A2,...,As)=H(A1)+A(A2|A1)+H(A3|A1A2)+...+H(A1A2...As-1),

где энтропия каждой последующей системы вычисляется при условии, что состояние всех предыдущих известно.

7) Полная условная энтропия системы H(B|A) не превышает её безусловной энтропии

Н(В): Н(А,В) Н(А)+Н(В)

Из этих свойств следует, что энтропия может служить мерой неопределенности состояния физической системы.

Относительная энтропия (коэффициент сжатия информации) h=H/Hmax. Относительная энтропия определяет относительную степень информационной загруженности системы. Она может характеризовать степень близости закона распределения к равномерному распределению.

Если события равновероятны и статистически независимы, то оценки количества информации, по Хартли и Шеннону, совпадают. Это свидетельствует о полном использовании информационной ёмкости системы. В случае неравных вероятностей количество информации, по Шеннону, меньше информационной ёмкости системы. Количество информации только тогда равно энтропии, когда неопределенность ситуации снимается полностью.

Из свойств энтропии следует, что она является мерой неопределенности состояния физической системы. Естественно поэтому количество информации измерять уменьшением энтропии системы, для уточнения состояния которой предназначены сведения. В теории информации физическую систему А, которая может в каждый момент времени случайным образом принять одно из конечного множества возможных состояний ai, называют дискретным источником сообщений. Каждое возможное состояние ai называют элементарным дискретным сообщением. Набор элементарных сообщений называют сообщением. При этом в течение некоторого времени источник может выдать дискретное сообщение в виде последовательности элементарных дискретных сообщений, представляющей сбой набор символов аi, каждый из которых имеет длительность ti секунд, необязательно одинаковую для различных i. При выдаче источником сообщений в виде последовательности элементарных дискретных сообщений, полное вероятностное описание дается вероятностью совместного появления набора различных символов аi в

называется стационарным. Если при определении вероятностных характеристик стационарного источника усреднение по ансамблю можно заменить усреднением по времени, то такой источник называется эргодическим. Вероятностные свойства

http://profbeckman.narod.ru/

эргодического источника можно оценить, рассматривая лишь одну его достаточно длинную реализацию.

Информационная энтропия – математическое ожидание H( ) случайной величины характеризует среднее значение количества информации, приходящееся на один символ.

Информационная энтропия дискретной случайной величины, , которая может принимать значения 1, 2,..., n, равна величине

Информация – содержание сообщения, понижающего неопределенность некоторого опыта с неоднозначным исходом; убыль связанной с ним энтропии является количественной мерой информации. В случае равновероятных исходов информация равна логарифму отношения числа возможных исходов до и после (получения сообщения).

Замечание. В статистической механике энтропия характеризует неопределенность, связанную с недостатком информации о состоянии системы. Наибольшей оказывается энтропия у равновесной полностью беспорядочной системы – о её состоянии наша осведомленность минимальна. Упорядочение системы (наведение какого-то порядка) связано с получением некоторой дополнительной информации и уменьшением энтропии. В теории информации энтропия также отражает неопределенность, однако, это неопределенность иного рода – она связана с незнанием результата опыта с набором случайных возможных исходов. Хотя между энтропией в физике и информатике много общего, необходимо сознавать и различие этих понятий.

Информация опыта равна среднему значению количества информации, содержащейся в каком-либо одном его исходе (среднее количество информации, приходящееся на один сигнал, удельная информативность источника). Это статистическое определение понятия «информация». Энтропия, рассчитанная по этой формуле, называется количеством информации или двоичной информацией.

Максимальное значение энтропии достигается при равенстве всех pi равны, т.е. p1=p2=…=pm=1/m. При этом выражение для энтропии равновероятных, независимых элементов равно: Hmax log2 m.

Энтропия численно совпадает со средним количеством информации, но смысл х различен, так как:

-энтропия выражает среднюю неопределенность состояния источника и является его объективной характеристикой, она может быть вычислена априорно, т.е. до получения сообщения при наличии статистики сообщений.

-информация определяется апостериорно, т.е. после получения сообщения. С получением информации о состоянии системы энтропия снижается.

Количество информации, содержащейся в дискретном сообщении, измеряется величиной исчезнувшей неопределенности. Мера этой неопределённости должна удовлетворять ряду условий: монотонное её возрастание с увеличением возможности выбора (объема алфавита источника n) и адитивность.

Замечание. Шеннон много внимания уделял информации, но никак её не обозначал. У него нет ни одной формулы с использованием этого параметра. Мы будем обозначать количество информации буквой Y.

Количество информации есть уменьшение энтропии вследствие опыта или какоголибо другого акта познания. Информация, которую необходимо получить, чтобы устранить неопределенность ситуации, равна двоичному логарифму числа равновероятных состояний системы. Но эта информация появляется только после необходимого числа испытаний. А до опыта эта величина является мерой неопределенности нашей системы и называется её энтропией. Убыль этой величины в результате испытаний и есть та информация о системе, которой мы владеем на данный

http://profbeckman.narod.ru/

момент. Если энтропия до начала опыта H1, а в результате сообщения информации Y энтропия становится равной H2 (H1 H2), то информация

т.е. информация равна убыли энтропии (количество информации измеряется изменением (уменьшением) неопределенности состояния системы).

Связь между информацией и информационной энтропией поясним на примере. Классические компьютеры работают в двоичной логике ”1” и ”0” (есть напряжение

в ячейке или нет). В этом случае считают, что каждая ячейка содержит один бит информации. Регистр из N ячеек содержит N бит информации. С их помощью можно записать 2N сообщений. Если все сообщения равновероятны, то вероятность каждого сообщения wN=1/2N. Введем информационную энтропию по формуле: H=-log2 wN. Для нашего простейшего случая H=N. На самом деле, есть сообщения более вероятные и менее вероятные.

В общем случае, если имеется набор из N величин xl, каждая из которых может появляться с вероятностью 1 р(xl) 0, то энтропия Шеннона

l 1

N

где р xl 1.

l 1

Информацию Шеннона измеряют в натах: 1 бит=1 нат/ln2 1,44 нат.

Если все сообщения равновероятны, то до прочтения содержания регистра нет информации о том, какое из 2N сообщений в нём записано. Пусть Y – мера информации. Тогда до прочтения регистра Yin=0, но энтропия Hin=N. Когда сообщение из регистра прочитано, то мы стали обладать информацией в N бит, т.е. Yfin=N. При этом мы точно

Информационную энтропию можно рассматривать как меру недостатка информации о классической системе. Чем меньше энтропия, тем больше информация. В этом случае говорят о том, что система упорядочена. Чем больше энтропия, тем меньше информации о системе: система движется к хаосу.

Замечание. Во многих книгах и даже учебниках почему-то утверждается, что информация равна энтропии. Это, конечно, не так. Сумма информации и энтропии равна константе (правда, есть учёные, утверждающие, что это не так, особую ненависть вызывает формула H+Y=1). Не информация равна энтропии, а изменение информации (дифференциал) равно изменению информации, причём с обратным знаком. Не надо путать скорость машины, с пройденным ею расстоянием!

Если изначально равновероятных исходов было n1, а в результате передачи информации Y неопределенность уменьшилась, и число исходов стало n2 (n2 n1), то

внимание Н. Виннер), отличаясь от неё отсутствием константы Больцмана (что сразу делает её безразмерной, тогда как термодинамическая энтропия имеет размерность теплопроводности) и знаком минус (что сразу подвигло многих учёных ввести понятие отрицательной (него) энтропии, однако вскоре от таких попыток отказались).

http://profbeckman.narod.ru/

Замечание 1. Шеннон полагал, что информационная энтропия точно совпадает с информацией (обе величины считаются по одной и той же формуле и исчисляются в одинаковых единицах!), но противостоит термодинамической энтропии Больцмана-Планка: информация Шеннона есть отрицательная термодинамическая энтропия. Тем более удивительно, что часто информацию представляют не как энтропию и не как отрицательную энтропию, а как обратную энтропию, т.е. как частное от деления единицы на энтропию (в последнее время обратную энтропию стали называть не информацией, а аниэнтропией; в немецкой литературе такую величину называют ordnung – порядок).

Замечание 2. В работах Шеннона информация и энтропия не противопоставляются друг другу (поскольку это одно и тоже); информация, как таковая, Шеннону не нужна - энтропии более чем достаточно; нигде Шеннон не связывает энтропию с беспорядком, а информацию с порядком: у него - энтропия - мера неопределённости и ничего другого!

Замечание 3. Формулы для информации и энтропии совпадает, поэтому, по крайней мере физике и химии понятие "информация" ничего не даёт. В этих науках не нужна ни информация, ни негэнтропия – энтропия вполне описывает физико-химические процессы. Утверждения, что энтропия якобы вводится только для процессов, стремящихся к равновесию, к порядку, а информация способна интерпретировать процессы самоупорядочения, не выдерживает критики: ничто не мешает распространить понятие энтропии на открытые системы, на сложные системы и на процессы, идущие с уменьшение энтропии. Понятие информации бесполезно и здесь. Энтропии вполне достаточно. Да, на основе представлений об информации можно вывести все равновесные статистические распределения, беда в том, что они были получены задолго до возникновения информационных идей.

Поскольку все w(xl) неотрицательны и не превосходят единицы, то очевидно, что H(X)≥0. Равенство достигается, когда w(xk)=1 и w(x1)=. . .=w(xk−1)=w(xk+1)=. . .=w(xN)=0. Теперь найдем максимальное значение энтропии H(X). Из условия нормировки вероятности имеем:

N 1

Энтропия Шеннона лежит в диапазоне 0H(X)ln(N), где N – количество элементов в ансамбле Х.

Если некая система A недоступна для наблюдения, то выясняется состояние не самой системы A, а системы B, связанной с системой A. Полной информацией о системе A,

информации о системе B, содержащейся в системе A YB A= YA B. Поэтому информацию YB A обозначают YB A и называют взаимной информацией. Полная взаимная информация, содержащаяся в двух системах, равна сумме энтропий составляющих систем минус энтропия объединенной энтропии:

Полная информация, содержащаяся в независимых системах, равна нулю YB A=0. Полная информация, содержащаяся в полностью зависимых системах, равна полной информации системы А, либо системы В YB A=Н(А)=Н(В)=YA=YB. Полная взаимная

http://profbeckman.narod.ru/

информация, содержащаяся в системах, из которых одна является подчиненной, равна энтропии подчиненной системы.

Количество информации, содержащееся в сообщении из n символов, равно:

Пример 1. Энтропия системы А, обладающей двумя состояниями А1 и А2 с вероятностями p1=p2=0,5 равна H(A)=-(0,5·log20,5+0,5·log20,5)=1, т. е. одному биту. Подбрасывание монеты -

случайный процесс, с 2-мя исходами, вероятность =50%, энтропия (и информация) 1 бит. Чтобы узнать исход броска монеты требуется количество информации 1 бит. Подбрасывание монеты n раз, приводит к случайной последовательности с энтропией равной n бит. В случае броска монеты известно, что следующий бит будет либо нулем (орел), либо единицей (решка), но не более того: монета абсолютно непредсказуема. В этом случае случайно возникшая цепочка битов содержит количество информации, равное ее длине. Но предположим, что монета, которую мы используем, фальшивая, и на вероятность выпадения орла приходится 70%. В этом случае каждый бит будет содержать немного меньше информации, поскольку мы знаем, что более вероятно выпадение орла. Крайний случай – это цепочка, состоящая из единиц. Если мы знаем, что при броске всегда выпадает решка, то, подбрасывая монету, не получаем вообще никакой информации. Здесь цепочка битов полностью предсказуема, содержание информации в ней нулевое.

Пример 2. Случайным образом вынимается карта из колоды в 32 карты. Какое количество информации требуется, чтобы угадать, что это за карта? Здесь n=25, значит, k=5 и Y=5 бит. Пример 3. При угадывании результата броска игральной кости задается вопрос «Выпало 6?». Какое количество информации содержит ответ? p=1/6, 1-p=5/6, Y=- 1/6; log21/6-5/6log25/6 0,65 бит. Пример 4. Допустим что кость фальшивая и вероятность любой грани пропорциональна числу на ней. Чему тогда равна энтропия. 1) H(x)=сумма p(xi)*log(1/p(xi)) 6*1/6*log 6=0,778 2) вероятность выпадения каждой кости равны, p(x1)=1/21;p(x2)=2/21; p(x3)=1/7, p(x4)=4/21; p(x5)=5/21; p(x6)=2/7 H(x)=1/21*log 21+2/21*log (21/2)+ 1/7*log(7) +4/21*log(21/4)+5/21*log(5/21)+2/7*log(7/2)=0,72

Энтропия достоверного события равна 0 бит, энтропия невозможного события равна 0 бит, потому что оба они не случайны.

Пример 5. Определить количество информации в сообщении из 8 двоичных символов (n=8, m=2), если вероятности равны: pi0=pi1=1/2. Количество информации равно: Y= n log m=8 log22=8 бит. Пример 6. Определить количество информации в сообщении из 8 двоичных символов (n=8, m=2), если вероятности равны: pi0=3/4; pi1=1/4.

Количество информации, заключенной в сообщении, измеряется уменьшением энтропии системы под действием этого сообщения.

Пример 7. До поступления сообщения энтропия системы равна 2 бит, а после него стала равной 1 бит. Информация, заключенная в сообщении, =1 бит.

Понятию "информация в битах" можно дать наглядное истолкование: она равна числу ответов "да" и "нет" на разумно поставленные вопросы, с помощью которых можно получить ту же информацию.

Рис. 2. Энтропия всегда положительна или равна нулю.

Пример 8. Определить частную информацию, полученную в сообщении наугад выбранного прохожего: “сегодня мой день рождения”. Так как вероятность сообщения р=1/365то частная информация от данного

сообщения Y=-log(1/365)= log365=8,51 бит.

http://profbeckman.narod.ru/

Пример 9. Определить среднюю информацию, полученную в сообщении: “сегодня мой день рождения или сегодня не мой день рождения”. Система имеет два возможных состояния: A1 – день рождения с вероятностью р1=1/364 и A2 – не день рождения с вероятностью р2=364/365. Средняя информация YA=H(A)=-(1/365)log(1/365)-(364/365)log(364/365) бит.

Пример 10. Если система А может иметь два равновероятных состояния: А1 и А2., то полное выяснение состояния этой системы несет информацию 1 бит, и, значит, можно ее получить в результате ответа на один вопрос. Вопрос "Находится ли система в состоянии А1?" и получив на него ответ "да" или "нет", позволяет выяснить состояние системы.

Пример 11. Имеется шахматная доска, на одну из клеток которой поставлена фигура (слон). Предположим, что все клетки выбираются с одинаковой вероятностью. Определим информацию, заключенную в сообщении о том, где стоит слон. У системы А (слон) 64 равновероятных

состояния; ее энтропия равна: Y (A) log2 1 6 бит.

64

Значит, сообщение, полностью устраняющее неопределенность состояния системы (указание, где стоит слон), должно содержать ровно шесть битов информации. А из этого следует, что положение слона можно точно выяснить с помощью не более чем шести вопросов.

Пример 12. Энтропия английского текста лежит между 1.0 и 1.5 битами на букву.

Пример 13. Статистика бросания монеты с заданной вероятностью выпадения орла или решки, описываемая распределением Бернулли. В точках 0 и 1 энтропия равна нулю. Нет никакой неопределенности, всегда выпадает одна и та же сторона монеты. Максимальная же энтропия достигается в точке 0.5 (выпадение орла и решки равновероятно). Чем больше энтропия распределения, тем распределение более равномерно. Отсюда следует, что из всех распределений, соответствующих эмпирическим данным, следует выбирать распределение, обладающее наибольшей равномерностью (наибольшей энтропией).

Пример 14: Имеются два ящика, в каждом из которых по 12 шаров. В первом – 3 белых, 3 черных и 6 красных; во втором – каждого цвета по 4. Опыты состоят в вытаскивании по одному шару из каждого ящика. Что можно сказать относительно неопределенностей исходов этих опытов?

Энтропии обоих опытов:

> , т.е. неопределенность результата в опыте β выше и, следовательно, предсказать его можно с меньшей долей уверенности, чем результат α.

Пример 15. Поток излучения Солнца у поверхности Земли составляет ∆Q ∆t≈1,4·106 эрг/см2 сек (так называемая солнечная постоянная). Этот поток излучения, в конечном счете, преобразуется в тепловую энергию атомов и молекул со средней температурой <T> 300 K. Тогда поток изменения энтропии от Солнца у поверхности Земли равен:

где k – постоянная Больцмана.

Потоку солнечной энтропии должен соответствовать поток информации

Этот поток влияет на показания приборов и его надо учитывать.

Информация бывает двух видов: макро и микро.

Макроинформация – это запомненный выбор. Запомнить (зафиксировать) информацию, означает привести систему в определенное устойчивое состояние. Ясно, что таких состояний должно быть не меньше двух. Каждое из них должно быть достаточно устойчивым, в противном случае система может самопроизвольно выйти из того или иного состояния, что равносильно исчезновению информации. Простейшая запоминающая система содержит всего два устойчивых состояния и называется триггер (переключатель). Этот элемент играет важную роль во всех информационных системах.

http://profbeckman.narod.ru/

Свойством запоминания могут обладать только макроскопические системы, состоящие из многих атомов. Запомнить что-либо, располагая одним атомом, невозможно, поскольку атом может находиться лишь в одном устойчивом (основном) состоянии. Макроинформация может содержаться только в макрообъектах.

Граница между макро и микро объектами проходит на уровне макромолекул, размеры которых порядка нанометров (10-9 м).

Микроинформация принципиально не запоминаема. Примером служит выбор одного микросостояния идеального газа в состоянии термодинамического равновесия. Выбор микросостояния означает, что удалось в определенный момент времени t измерить координаты и скорости всех молекул с определенной точностью. Однако выбранное состояние тут же (за время t~10-13 сек) , будет забыто, сменится другим микросостоянием, выбранным по закону случая. Это свойство – забывать предыдущее микросостояние – является фундаментальным для эргодических систем, в которых средние по времени совпадают со средними по ансамблю. Именно оно понимается под словами «молекулярный хаос» и именно оно лежит в основе термодинамики. Количество микроинформации в данном примере велико:

Ymicro=log2n=-log2w, (24)

где nmicro – число микросостояний, w=1/nmicro – вероятность случайно выбрать какое-либо одно из них. Количество макроинформации в том же примере, напротив мало: Ymаcro=log2 nmаcro=0, поскольку макросостояние равновесного газа единственно, то есть nmаcro=1. Разумеется, макроинформация не может быть ни ценной, ни смысловой и вообще не может использоваться, как информация в реальной жизни. Тем не менее, она широко обсуждается и является источником многих недоразумений. Из внешней аналогии формул Больцмана и Шеннона следует термодинамическая энтропия и микроинформация пропорциональны друг другу. Связь между энтропией и микроинформационной имеет вид

Количество информации до измерения, когда выбор еще не сделан Ymicro(t)=0 , поэтому прирост количества макроинформации Ymicro=+Ymicro. Отсюда делается вывод:

S k Y

При увеличении информации о системе ее энтропия уменьшается. Энергия kT/1,44

– минимальная цена одного бита микроинформации (1,44 – коэффициент перехода от натуральных логарифмов к двоичным).

Микроинформация существенно отличается от макроинформации, поскольку она не имеет важного для информации свойства фиксируемости, ибо незапоминаема, отличается она не только качественно, но и количественно. Это ясно, если вернуться от

Yмикро – огромное число, ибо k=1,38 10-23 Дж/К ( S<0), Yмaкро<<-( S/k)log2e.

Запоминание – процесс макроскопический и диссипативный, он сопровождается большим изменением энтропии. В случае макроинформации число устойчивых состояний системы, n, невелико. В случае микроинформации полное число микросостояний (неустойчивых, то есть микроскопических), n, огромно.

В реальной жизни всегда используется макроинформация, которую называют просто информацией.

Любое изменение макроинформации, увеличение или уменьшение, сопровождается ростом энтропии, что естественно, поскольку эти процессы необратимы. Количественной связи между изменениями макроинформации и термодинамической энтропии не существует. Энергетическая цена макроинформации определяется энергией, диссипирующей в процессе запоминания и зависит от конкретных условий, в частности от

http://profbeckman.narod.ru/

времени на которое информацию нужно запомнить, то есть от свойств ячейки памяти. Эта энергия, приходящаяся на один бит информации, заведомо (и много) больше kТ/1,44 – энергии одного бита микроинформации.

В теории информации важную роль играет ансамбль X2, который состоит всего из двух элементов x1 и x2, каждый из которых возникает с вероятностью w(x1)=p и w(x2)=1-p соответственно (0≤p≤1). Энтропия такого ансамбля

H(X2)≡H(p)=-p ln p-(1-p) ln(1-p) (28)

носит название двоичной энтропии.

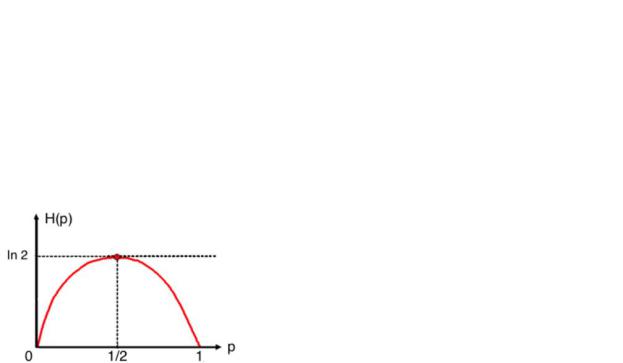
Очевидно, что двоичная энтропия обладает симметрией относительно значения p=1/2, т.е. H(p)=H(1-p). Легко проверить, что максимальное значение двоичной энтропии Hmax=ln2 достигается при p=1/2, минимальное – Hmin=0 – при p=0 и p=1. При увеличении р величина энтропии возрастает вплоть до р=0,5, а затем падает до нуля. Максимум энтропии достигается тогда,

когда все исходы равновероятны.

Рис. 3. Зависимость энтропии Шеннона от вероятности события.

Из графика видно, что двоичная энтропия является вогнутой функцией (то есть любая прямая, соединяющая две точки на графике лежит ниже графика самой функции H(p)). Отсюда

H(px1+(1-p)x2)≥ pH(x1)+(1-p) H(x2). Равенство достигается только если x1=x2 или p=0, или p=1. Данное свойство называется вогнутостью двоичной энтропии.

Энтропия Шеннона количественно характеризует произвольное распределение какого-либо параметра системы – энергии, скорости, числа атомов в разных состояниях возбуждения и др. Если в системе происходят какие-либо изменения, то меняются распределения ее параметров. Соответственно, изменяется и величина энтропии. В этом смысле энтропия Шеннона является функцией состояния системы, так как количественно характеризует меру неопределенности значений параметров.

Количество информации, передаваемое в сообщении, тесно связано с мерой неопределенности передаваемых символов. Чем больше число способов (микросостояний), с помощью которых, можно реализовать тождественно одну и ту же макроскопическую систему (объект), тем однозначнее и точнее она определена, тем больше информации о ней отражает факт её существования. Энтропия – мера беспорядка в том смысле, что чем больше энтропия объекта, тем меньше его существование зависит от деталей микросостояний, т. е. этот объект воспроизводим в природе тем точнее, чем больше число ответственных за него равновероятных микросостояний. Интуитивно такая неопределённость ассоциируется с понятием о беспорядке.

Энтропия является косвенной мерой порядка системы; чем выше энтропия, тем более равномерно и случайным образом распределены компоненты системы. Чтобы както связать энтропию с беспорядком, а информацию с порядком вводятся понятия неслучайной и случайной информации. Тогда энтропия – мера количества случайной информации, вводимой в случайный процесс (она тесно связана с числом возможностей случайного процесса). Общий объём информации равен сумме количества случайной информации и количества неслучайной информации. Чем больше случайной информация находится в системе, тем выше энтропия системы.

В результате получения сведений неопределенность случайного объекта может быть только уменьшена. Поэтому количество информации измеряют уменьшением энтропии того объекта или системы, для уточнения состояния которого предназначены сведения. Если состояния объекта обладают различными вероятностями, информации от разных сообщений неодинаковы: наибольшую информацию несут сообщения о тех состояниях, которые априори были наименее вероятны. Например, сообщение о том, что в

http://profbeckman.narod.ru/

Москве в прошлом году не было землетрясения, несёт меньше информации, чем сообщение, что оно было.

Часто можно встретить утверждение о том, что информация – мера упорядоченности.

Здесь нужно уточнить, какая именно информация (ценная или нет, условная или безусловная) имеется в виду, а также, что понимается под словом «порядок». В действительности в приведенном утверждении неявно предполагается, что информация ценная, но в этом случае она наверняка условная, ибо зависит от цели. Понятие «порядок» тоже целесообразно. Так, если цель – прогноз, то упорядоченными следует считать системы, развивающиеся устойчиво и допускающие предсказание результатов. Именно в этом смысле в физике хаотические системы считаются беспорядочными и энтропия здесь выступает как мера беспорядка.

На практике часто встречаются физические системы, аналогичные непрерывным случайным величинам. Состояния таких систем нельзя перенумеровать и каждое отдельное состояние имеет вероятность, равную нулю. Такие системы называют непрерывными системами, в отличие от рассмотренных выше дискретных систем.

Информационная энтропия непрерывной одномерной случайной величины х с

функцией распределения f(x):

Дифференциальная энтропия – формальное обобщение понятия информационной энтропии Шеннона для случая непрерывной случайной величины. В теории информации интерпретируется как средняя информация непрерывного источника.

Дифференциальная энтропия неинвариантна к преобразованию координат случайной величины и не имеет самостоятельного смысла. Если случайная величина имеет размерность, то функционал дифференциальной энтропии будет некорректен с точки зрения размерности (поскольку под знаком логарифма оказывается размерная величина). Однако разность дифференциальных энтропий двух случайных величин, распределенных на одном интервале, является безразмерной величиной и совпадает с разностью их энтропий (энтропия любой непрерывной случайной величины бесконечна).

Полная взаимная информация системы (А,В):

Полная взаимная информация, как и в случае дискретных систем, есть неотрицательная величина, обращающаяся в нуль только тогда, когда системы А и В независимы.

Условная дифференциальная энтропия величины Апри заданной величине В:

положительными, так и отрицательными величинами, а также могут быть равны бесконечности.

Остановимся на понятии условной энтропии несколько подробнее.

Если две случайные величины A и B, каким-то образом связанные друг с другом (например, на входе и выходе какой-то системы), то знание одной из них, очевидно уменьшает неопределенность значений другой. Остающаяся неопределенность

http://profbeckman.narod.ru/

оценивается условной энтропией. Так, условная энтропия A при условии знания B определяется как:

где p(Ai|Bk) – условные вероятности (вероятность i-го значения A при условии B=Bk), диапазоны изменчивости A и B (соответственно N и K) не обязательно совпадают.

Чтобы рассчитать H(A|B), находят К энтропий A, соответствующих фиксированному Bk и затем суммируют результаты с весами p(Bk). Очевидно, условная энтропия меньше безусловной, точнее: 0 H(A|B) H(A). Нижняя грань соответствует однозначной зависимости A от B, верхняя – полной независимости.

Информация определяется разностью между безусловной и условной энтропиями. Это уменьшение неопределенности “знания чего-то за счет того, что известно что-то”. При этом замечательно, что информация Y симметрична, т.е. YAB=YBA:

однозначная зависимость. Таким образом, безусловная энтропия – это максимальная информация, потенциально содержащаяся в системе. Зависимость однозначная, но не взаимно-однозначная: несмотря на симметрию, верхние грани YAB и YBA отличаются: 0 YAB H(A), 0 YBA H(B).

К сожалению, зная количество информации, нельзя написать уравнение связи переменных (тогда как корреляция позволяет легко переходить к регрессии). Можно определить совместную энтропию A и B по их двумерному распределению. При этом:

Аддитивность и субаддитивность – характеристики отношений между целым и его частями. Аддитивность – такое отношение , при котором свойствам целого полностью определяются свойствами частей («целое равно сумме частей»); Субаддивность (неаддитивность) – отношение, при котором целое не определяется его частями, так что оно не может быть познано и объяснено на основе одного лишь знания о его частях («целое больше суммы его частей»).

Энтропия субаддитивна, аддитивность (H(AB)=H(A)+H(B)) достигается только при полной независимости A и B. С помощью совместной энтропии можно написать выражение для информации YAB=YBA=Y в симметричном виде:

Рис. 4. Наглядная связь между различными энтропиями и взаимной информацией

Для дифференциальной энтропии справедливы равенства, аналогичные для энтропии дискретного источника:

H(A) H(B|A) (для независимых источников — равенство)

H(A,B)=H(A)+H(B|A)=H(B)+H(A|B) (38)

Очевидно, что можно узнать больше информации о наборе А, если известна информация о наборах В и С, которые каким то образом связанны с набором А (например, при помощи совместных распределений вероятностей или найденных на опыте эмпирических корреляций), чем когда известна информация только об одном таком наборе В. В силу соотношения между энтропией и информацией для условной энтропии