
- •Аннотация
- •От автора
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •1. СИСТЕМЫ И ПРОЦЕССЫ
- •2. ПОРЯДОК, НЕПОРЯДОК, БЕСПОРЯДОК И ХАОС
- •3. ТЕРМОДИНАМИКА
- •3.1 Начала термодинамики
- •3.2 Равновесная термодинамика
- •4. НЕРАВНОВЕСНАЯ ТЕРМОДИНАМИКА
- •4.1 Диссипативные структуры, системы и среды
- •4.2 Термодинамика необратимых процессов
- •4.3 Линейная неравновесная термодинамика
- •4.4 Нелинейная неравновесная термодинамика
- •4.5 Статистическая термодинамика
- •5. ЭНТРОПИЯ
- •5.1 Определение и свойства энтропии
- •5.2 Энтропия в химической термодинамике
- •5.3 Энтропия в статистической физике
- •5.3.1 Энтропия Больцмана-Планка
- •5.3.2 Энтропия Гиббса
- •5.4 Тсаллис (Цаллис) энтропия (Революция в термодинамике)
- •6. ГЕОМЕТРИЯ ФРАКТАЛОВ
- •6.1 Элементы геометрии фракталов
- •6.2 Размерности фракталов
- •6.3 Примеры фракталов
- •6.4 Фракталы и энтропия
- •7. ИНФОРМАТИКА
- •7.1 Информация, информатика и информационные технологии
- •7.2 Теория информации
- •7.2.1 Информация Хартли
- •7.2.2 Энтропия Шеннона
- •7.3 Отрицательная энтропия, антиэнтропия, экстропия
- •7.4 Алгоритмическая теория информации
- •7.4.1 Энтропия Колмогорова
- •7.4.2 Эпсилон-энтропия
- •7.5 Энтропия Кульбака-Лернера
- •7.6 Энтропия Реньи
- •7.7 Квантовая информатика
- •7.7.1 Некоторые положения квантовой механики
- •7.7.2 Энтропия фон Неймана
- •7.7.3 Линейная энтропия
- •7.7.4 Сравнение энтропий Реньи, Цаллиса и Неймана
- •7.7.5 Энтропия Холево
- •8. СИНЕРГЕТИКА
- •8.1 Синергизм и синергетика
- •8.2 Детерминизм, случайность и неопределённость
- •8.3 Простые и сложные системы
- •8.4 Анализ систем
- •8.5 Параметры порядка (управляющие параметры)
- •8.6 Процессы самоорганизации
- •9. СИСТЕМЫ И ЗАКОНЫ ИХ ЭВОЛЮЦИИ
- •9.1 Статические системы
- •9.2 Динамические системы
- •9.3 Линейные динамические системы
- •9.4 Нелинейные динамические системы
- •9.5 Эволюция динамической системы
- •9.6 Математическое описание эволюции динамической системы
- •10. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ОПИСАНИИ ДИНАМИЧЕСКИХ СИСТЕМ
- •10.1 Обыкновенные дифференциальные уравнения
- •10.2 Фазовое пространство и пространство состояний
- •10.3 Линейные ОДУ на плоскости
- •10.4 Нелинейные дифференциальные уравнения
- •11. ОТОБРАЖЕНИЯ
- •11.1 Системы с дискретным временем в отображениях
- •11.2 Итерации в исследовании динамических систем
- •11.3 Графические методы нахождения неподвижных точек и исследования их свойств
- •11.4 Многопараметрические отображения
- •11.5 Примеры некоторых важные отображений
- •12. ОСОБЫЕ ТОЧКИ ФАЗОВЫХ ПОРТРЕТОВ ДИНАМИЧЕСКИХ СИСТЕМ
- •12.1 Дифференциальные уравнения и особые точки
- •12.2 Классификация точек равновесия
- •12.3 Фазовые портреты и особые точки нелинейных ОДУ
- •12.4 Многомерные системы
- •13. РЕГУЛЯРНЫЕ АТТРАКТОРЫ И РЕПЕЛЛЕРЫ
- •13.1 Типы аттракторов
- •13.2 Фазовый объём
- •13.3 Репеллеры
- •13.4 Осциллятор и осцилляции
- •14. УСТОЙЧИВОСТЬ ДИНАМИЧЕСКИХ СИСТЕМ
- •14.1 Устойчивые и неустойчивые равновесия
- •14.2 Устойчивость по Ляпунову (метод первого приближения)
- •14.3 Показатель Ляпунова
- •14.4 Устойчивость нелинейной системы
- •14.5 Метод функций Ляпунова
- •14.6 Функция Ляпунова и энтропия
- •14.7 Асимптотическая устойчивость
- •14.8 Устойчивость особых точек
- •14.9 Устойчивость особых точек
- •14.10 Устойчивость решений дискретных уравнений
- •15. БИФУРКАЦИИ
- •15.1 Бифуркации: основные понятия и классификация
- •15.2 Элементы теории бифуркаций
- •15.3 Простейшие бифуркации
- •16. БИФУРКАЦИИ ЦИКЛОВ
- •16.1 Предельные циклы
- •16.2 Устойчивость предельных циклов
- •16.3 Бифуркации устойчивых предельных циклов
- •16.5 Бифуркация рождения пары устойчивых замкнутых траекторий.
- •16.6 Транскритическая (обмена устойчивостью между циклами) бифуркация.
- •16.7 Бифуркация исчезновения (рождения) пары замкнутых траекторий.
- •16.8 Бифуркация удвоения периода цикла
- •16.9 Бифуркация рождения (гибели) двумерного тора.
- •16.10 Гомоклиническая бифуркация рождения/исчезновения цикла
- •17. ДИНАМИЧЕСКИЙ ХАОС
- •17.1 Хаос статистический и динамический
- •17.2 Предсказание статического поведения системы
- •17.3 Сценарии перехода к хаосу
- •17.4 Примеры систем с хаосом
- •18. ХАОС В ЛИНЕЙНЫХ ОДНОМЕРНЫХ СИСТЕМАХ
- •18.1 Бифуркационные диаграммы
- •18.2 Лестница Ламерея
- •18.3 Отображение Бернулли
- •18.4 Треугольное отображение
- •18.5 Отображение «тент»
- •18.6 Канторов репеллер
- •18.7 Детерминированная диффузия
- •19. ХАОС В ЛОГИСТИЧЕСКОМ ОТОБРАЖЕНИИ
- •19.1 Переход к хаосу через удвоение периода
- •19.2 Логистическое уравнение
- •19.3 Дискретное логистическое уравнение
- •19.4 Логистическое отображение
- •19.5 Бифуркационная диаграмма логистического отображения
- •19.6 Цикл периода 3
- •19.7 Фазовые диаграммы логистического отображения
- •19.8 Аттракторы и фракталы в логистическом отображении
- •20. ХАОС В НЕЛИНЕЙНЫХ ОДНОМЕРНЫХ ОТОБРАЖЕНИЯХ
- •20.1 Отображение xn+1=С+xn2.
- •20.2 Отображение xn+1=а-xn2.
- •20.3 Подобие окон периодической динамики
- •20.4 Порядок Шарковского
- •20.5 Универсальность Фейгенбаума
- •20.6 Устойчивость циклов одномерных отображений
- •20.7 Топологическая энтропия
- •20.8 Синус-отображение
- •21. ХАОС В НЕЛИНЕЙНЫХ ДВУМЕРНЫХ ОТОБРАЖЕНИЯХ
- •21.1 Отображение Эно (Henon map)
- •21.2 Отображение подковы и отображение пекаря
- •21.3 Отображение «кот Арнольда» (Arnold’s cat map)
- •22. НЕРЕГУЛЯРНЫЕ АТТРАКТОРЫ
- •22.1 Хаос в консервативных и диссипативных системах
- •22.2 Регулярные и хаотические аттракторы
- •22.3 Квазиаттракторы
- •22.4 Хаотически аттракторы
- •22.5 Негиперболические хаотические аттракторы
- •22.6 Фрактальные аттракторы
- •22.7 Характеристика нерегулярных аттракторов
- •22.8 Странные нехаотические аттракторы
- •22.9 Сингулярные аттракторы
- •22.10 Многомерные нерегулярные аттракторы
- •22.11 Дикие аттракторы

http://profbeckman.narod.ru/
сохраняется до бесконечности. В предельном цикле ситуация совершенно другая. Здесь при любом начальном условии, динамическая система идёт к предельному циклу с определённой, наперёд заданной, амплитудой и частотой.
Циклы подверженные разного рода бифуркациям. Рассмотрим некоторые из них.
16.3 Бифуркации устойчивых предельных циклов
Кроме бифуркаций состояния равновесия в динамических системах при изменении параметра может происходить ещё одна перестройка структуры фазового пакета. Этот тип бифуркации рассматривает рождение предельного цикла из неподвижной точки.
Рассмотрим эффекты бифуркаций в семействе нелинейных автономных систем
ОДУ
|
m |
|
|
x M R , C |
|
(9) |
|
x F(x, ), |
|
заданных в фазовом пространстве М гладкими векторными полями F, зависящими от координат векторов системных параметров , лежащих в области L пространства R.
В случае, когда предельный цикл х0(t, ), имеющий период Т, является семйством уравнений (9) при всех U, то, линеаризуя семейство (9) на цикле, получим зависящую
от параметра систему ОДУ с периодической матрицей линейной части |
|
|
||||||||||||||||
|
( ) = |
( ) − |
, |
( , |
), |
)а= |
( |
+ , |
) |
|
|
(10) |
|
|
||||
где |
|
= ( , ) |
|
|
||||||||||||||
̇= |
( , |
) |
|
( |
, |
|
( |
( , |
) ) |
. При этом вектор у=0 является решением |
||||||||
системы (10) для всех μ U. |
|
|
|
|
|
|
|
|
|
|||||||||
|
Как следует из теории Флоке, каждое фундаментальное матричное решение |
|||||||||||||||||
линейной |
|
системы |
с периодическими коэффициентами представимо в виде |
|
||||||||||||||
|
|
|
|
где |
|
|
|
|
– |
некоторая, вообще говоря, комплексная |
периодическая |
|||||||
|
|
|
|
|
с( , |
|
|
Т- |
( , ) = |
|||||||||
матрица, |
а матрица |
|
) = exp( |
( |
) ) |
|
|
|
|
|||||||||
( |
, ) |
|
|
|
|
|
|
является фундаментальной матрицей линейной |
||||||||||
( , |
) ( |
, |
), |
|
|
|
|
|
|
|
|
|||||||
системы |
уравнений |
|
постоянными, |
вообще |
говоря, комплексными |
коэффициентами |
||||||||||||
̇= |
( ) |
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Устойчивость (неустойчивость) периодического решения определяется собственными значениями матрицы В – показателями Флоке исходного цикла или, что равносильно, собственными значениями действительной матрицы С=ехр(ВТ) – мультипликаторами цикла. Так как цикл устойчив при всех μ<0, то один показатель Флоке равен нулю, а все остальные m-1 показателей имеют отрицательные вещественные части (один простой мультипликатор имеет значение +1, а все остальные мультипликаторы имеют модули, меньшие 1, т. е. лежат внутри единичного круга плоскости комплексного переменного).
Следовательно, бифуркации, связанные с потерей устойчивости периодического решения семейства (9), могут произойти лишь в тех случаях, когда при μ=0 один или несколько показателей Флоке из m-1 пересекают мнимую ось слева направо или, что равносильно, один или несколько мультипликаторов, лежащих внутри единичного круга при μ<0, пересекают единичную окружность при μ=0. Бифуркации циклов могут иметь место, очевидно, только в системах уравнений размерности m>1.
Как и в случае особой точки, бифуркации, приводящие к потере устойчивости периодического решения семейства (9), определяются исключительно теми координатами системы, которые соответствуют собственным значениям матрицы В(0), лежащим на мнимой оси. Система уравнений, записанная в этих координатах, есть нормальная форма семейства (9) в окрестности периодического решения.
Определение нормальной формы и, соответственно, вида происходящей бифуркации периодического решения, является чрезвычайно сложной задачей. Так как мультипликатор цикла, соответствующий вектору ̇( ) всегда равен единице, а показатель Флоке – нулю и не является бифуркационным, то координаты нормальной формы заведомо лежат в гиперплоскости S, трансверсальной вектору ̇( ) и задаваемой последними m-1 компонентами вектора z(t). Обозначим этот вектор, имеющий на единицу

http://profbeckman.narod.ru/
меньшую размерность, чем исходный вектор y(t) линеаризованной на цикле системы (10), через v(t). Вектор v(t) удовлетворяет системе m-1 линейных дифференциальных уравнений
где |
|
̇( ) = |
|
( , |
) ( ) |
|
|
(12) |
|
|
|
|
|
|
|
|
(11) |
|
действительная матрица D(t, μ) получается из действительной матрицы |
|||||||
|
|
( , ) = |
( , ) ( , ) − |
( , ) ( , ) |
|
|||
вычеркиванием ее первой строки и первого |
столбца. Система (12) имеет те же показатели |
|||||||
̇ |
|
|||||||
Флоке, за исключением нулевого, что и исходная линеаризованная система. |
||||||||
( , |
Возможны два принципиально различных случая: случай постоянной матрицы |
|||||||
) = ( |
) |
и случай переменной |
Т-периодической матрицы D(t, μ). Первый случай |
|||||
|
|
|
|
|||||
означает, что матрицы Q(t,μ)-P(t, μ) и G(t, μ)=Β(μ) действительны, а показателями Флоке цикла, отличными от нулевого, являются собственные значения матрицы D(μ). Другими словами, первый случай означает, что переход преобразованием Q(t,μ) к системе координат, связанной с циклом, уже осуществляет приведение системы с периодическими коэффициентами к системе с постоянными вещественными коэффициентами. Вектор z(t) в этом случае совпадает с вектором u(t), а компонентами вектора v(t) являются последние m-1 компонент вектора u(t). Во втором случае имеет место более сложная ситуация.
Вслучае постоянной матрицы D(t,μ)=Q(μ) бифуркация цикла происходит при переходе либо одного вещественного собственного значения, либо двух комплексно сопряженных собственных значений матрицы D(μ) через мнимую ось. При этом все остальные собственные значения должны иметь отрицательные вещественные части. Этому случаю соответствуют четыре основные, наиболее часто встречающиеся в приложениях, бифуркации предельных циклов.
Фазовые траектории не могут пересекаться, поэтому динамика на плоскости не может быть хаотичной. Траектории, которые не уходят в бесконечность, могут либо притягиваться к неподвижным точкам, либо наматываться на предельные циклы (либо в консервативном случае быть замкнутыми). Если размерность фазового пространства n>2 динамика может быть гораздо более сложной.
Важным эффектом является разрушение бифуркаций при возмущениях.
Можно отметить, что бифуркация седло-узел и бифуркация Хопфа являются общими бифуркациями в динамических системах. При возмущениях (или незначительных несовершенствах в самой системе) транскритическая бифуркация и бифуркация вил переходят в бифуркацию седло-узел. Разрушение бифуркации вил приводит к одному равновесному состоянию, которое эволюционирует плавно, по мере увеличения параметра управления, к другому состоянию разъединения, которое существует выше критического значения параметра. Разъединённое состояние может быть достигнуто только путём прерывистого скачка параметра; оно катастрофически исчезает ниже критического значения параметра.
Известны разные виды бифуркаций, связанных с рождением предельного цикла: рождение предельного цикла из сложного фокуса; рождение предельного цикла из сложного предельного цикла; рождение предельного цикла из петли сепаратрисы; рождение предельного цикла из сепаратрисы положения равновесия седло–узел при его исчезновении; рождение предельного цикла из замкнутой неизолированной траектории и др. Приведём некоторые примеры.
16.4Бифуркация Пуанкаре-Андронова—Хопфа (бифуркация рождения цикла)
Втеории динамических систем бифуркация Андронова-Хопфа – локальная бифуркация векторного поля на плоскости, в ходе которой особая точка-фокус теряет устойчивость при переходе пары её комплексно-сопряжённых собственных значений через мнимую ось. При этом либо из особой точки рождается небольшой устойчивый предельный цикл (мягкая потеря устойчивости, мягкая, суперкритическая), либо, наоборот, небольшой неустойчивый предельный цикл в момент бифуркации схлопывается

http://profbeckman.narod.ru/
в эту точку, и её бассейн отталкивания после бифуркации имеет отделённый от нуля размер (жёсткая потеря устойчивости, жёсткая, субкритическая).
Данный тип бифуркаций встречается исключительно в нелинейных системах. Здесь устойчивый фокус через центр может переходить в неустойчивый фокус. При этой бифуркации в нелинейных системах происходит рождение предельного цикла, и система становится автоколебательной. При переходе параметра через бифуркационное значение это положение равновесия теряет устойчивость, однако в его окрестности появляется замкнутая асимптотически устойчивая траектория, характерный размер которой увеличивается при дальнейшем изменении параметра .
Бифуркация Хопфа возникает, когда периодическое решение или предельный цикл, окружающий точку равновесия, возникает или исчезает при изменении параметра μ. Когда устойчивый предельный цикл окружает неустойчивую точку равновесия, бифуркация называется сверхкритической бифуркацией Хопфа. Если предельный цикл неустойчив и окружает устойчивую точку равновесия, то бифуркация называется докритической бифуркацией Хопфа.
Бифуркации Хопфа возможны, только если система уравнений первого порядка
dx F(x; ) имеет размерность n≥2. Для плоского случая n=2 система уравнений dt
|
|
du |
|
|
||||||
|
|
|
|
|
f (u, v; |
|
||||
|
|
dt |
(13) |
|||||||
|
|
|
||||||||
|
dv |
|
g(u,v; ) |
|
||||||
|
|
dt |
|
|||||||
|
|
|
|
|||||||
где f и g – аналитические функции u, v и . |
|
|||||||||
Критические точки u0( ), v0( ) Ур.13 определяются |
|
|||||||||
|
|
f u0 ( ),v0 ( ) 0 |
(14) |
|||||||
|
|
|
|
|
|
|
|
|||
|
g u0 ( ),v0 ( ) 0 |
|
||||||||
Обычно эту нелинейную модель представляют в виде: |
|
|||||||||
|
dz |
j z x |
|
z |
|
2 , |
(15) |
|||
|
|
|
||||||||
|
|
|||||||||
|
|
dt |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
где z – комплексная переменная; +j – комплексный параметр, причём j – мнимая единица, – варьируемый бифуркационный параметр.
Уравнение представляет собой комплексный аналог бифуркации типа «вилка». С целью определения всех равновесных решений необходимо произвести замену
комплексной переменной z: |
|
z=x1+jx2 |
(16) |
где х1 и х2 новые вещественные переменные. |
|
В результате подстановки z в Ур.15 получается система из двух уравнений
(17)
Здесь осуществлён переход от модели второго порядка с вещественными параметрами. Полученные уравнения связаны между собой через комплексную переменную z и имеют следующие стационарные решения:
x1=x2=0 при z=0 |
|
(18а) |
x12+x22=|z|2= при z 0 |
|
(18б) |
Первое решение является неустойчивым и совпадает с точкой бифуркации, а |
||
второе решение определяет окружность радиуса |
|
в пространстве координат (x1,x2,μ). |
|
||
http://profbeckman.narod.ru/
Существуют разные формы записи систем уравнений для бифуркации Хопфа. Начнём с рассмотрения простой двумерной динамической системы с двумя управляющими параметрами и . В полярных координатах
dr |
|
r3 r |
|
|
|
||
dt |
(19) |
||
d |
|
||
|
|
||
|
|
||
dt |
|
||
где радиус r>0.
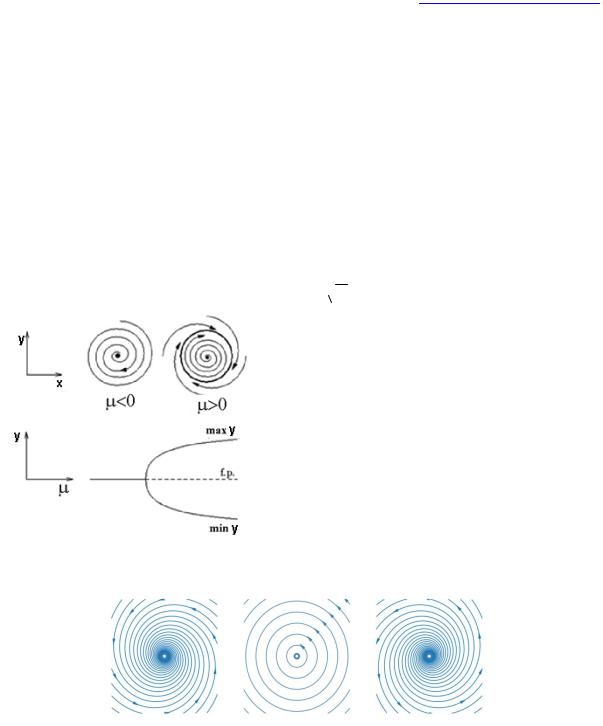
При 0 существует лишь тривиальное решение r0(1)0, которое является устойчивым. В фазовом пространстве с координатами x1 rcos и x2 r sin траектории будут стремиться к неподвижной точке x1 x20 (рис. 8). При 0 эта точка должна быть фокусом, в силу того, что угловая переменная меняется по закону 0+ t. При 0 тривиальное решение r0(1)0 также существует, но теперь оно неустойчиво. Однако появляется второе нетривиальное решение r02 
 , которое является устойчивым. В
, которое является устойчивым. В
фазовом пространстве x1, x2 такой случай будет представлен траекториями, удаляющимися по спирали от неподвижной точки и стремящимися к предельному циклу, наматываясь на окружность (рис. 8). В случае, когда исходная точка лежит в области r r0(2), траектории будут представлять собой спирали, сходящиеся к предельному циклу (окружности) извне.
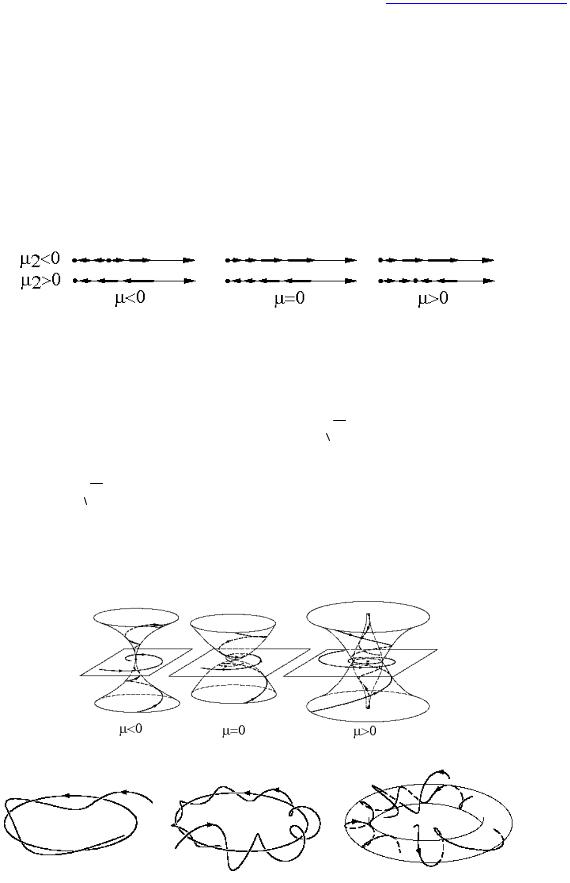
Рис. 8. Рождение предельного цикла при бифуркации Хопфа: фазовое пространство для бифуркации Хопфа (вверху); бифуркационная диаграмма, представлены как
максимальное так и минимальное значение х2 на периодической орбите. f.p. – неподвижная точка.
Рис. 9. Фазовый портрет семейства (20) при c=0 и ε<0 (слева), ε=0 (в центре), ε>0 (справа).
Бифуркация Хопфа включает в себя изменение устойчивости неподвижной точки динамической системы вместе с рождением периодической орбиты. Например, для бифуркации Хопфа, показанной на рис. 8, при <0 существует устойчивая неподвижная точка, а при >0 – неустойчивая неподвижная точка и устойчивая периодическая орбита. В системе (19) при =0 происходит бифуркация нового типа: из неподвижной устойчивой точки рождается устойчивый предельный цикл.

http://profbeckman.narod.ru/
Рис. 10. Фазовый портрет семейства (20) при 2<0 и 1<0 (слева), 1=0 (в центре) и 1>0 (справа).
Подобные бифуркации примечательны тем, что потеря устойчивости происходит мягко: по мере увеличения надкритичности (параметра ) вновь возникшие устойчивые решения плавно удаляются от решения, которое стало неустойчивым. Если, например, говорить про бифуркацию Хопфа, то амплитуда колебаний в возникающем предельном цикле плавно увеличивается от нуля пропорционально 
 .
.
Рис. 11. Фазовый портрет семейства (1) при c>0 и ε<0 (слева), ε=0 (в центре) и ε>0 (справа).
Поясним механизм возникновения цикла на примере систем уравнений
x x x |
2 |
x x2 |
y2 , |
|
||||
1 |
|
|
|
|
|
|
||
|
|
2 (x |
2 |
y |
2 |
). |
(20) |
|
y 1 y y |
|
|
||||||
где 1 и 2 - фиксированные параметры.
Рассмотрим сначала случай 2=0, при котором система является линейной. Собственные значения матрицы равны 1+i. Если 1<0, система имеет устойчивый фокус, при 1=0 – центр, при 1>0 – неустойчивый фокус (рис. 9).
Чтобы понять, как устроена динамика, снова перейдем в полярные координаты. Вместо полярного радиуса будем использовать его квадрат ρ=x2+y2. Имеем:
|
2 , |
(21) |
2 1 |
где >0.
Пусть теперь 20. В этом случае у системы появляется нелинейная часть. Чтобы Итак, по углу происходит вращение с постоянной угловой скоростью, но
расстояние до начала координат может меняться со временем. Рассмотрим два случая в зависимости от знака 2.
Нелинейное притягивание
Пусть 2<0. График правой части Ур.21 – парабола с ветвями, направленными вниз.
У неё обязательно есть корень ρ=0. Второй корень находится как * 1 , но при 1<02
мы получим отрицательное число, в то время как ρ обязано быть положительным. При1=0 оба корня совпадают и равны нулю. При 1>0 второй корень положителен и имеет смысл. При 1<0 динамика очень простая: ρ монотонно уменьшается со временем, фазовые кривые являются спиралями, приближающимися к началу координат, как в линейном фокусе (рис. 10). При 1=0 происходит примерно то же самое, только спирали

http://profbeckman.narod.ru/
наматываются чаще – мы уже сталкивались с этой системой, это медленный фокус. А вот при 1>0 происходит нечто новое. Для начальных условий ρ (0,ρ ) производная˙ρ положительна и значит, решения будут приближаться к началу координат с уменьшением t и убегать от него с ростом t. Но далеко они не убегут: по мере приближения ρ к значению ρ скорость «убегания» уменьшается, и траектория наматывается на окружность ρ=ρ изнутри. Если начальное условие лежит на этой окружности, то ρ не меняется со временем (это положение равновесия для Ур.21) и значит, траектория сама является окружностью. При ρ>ρ производная отрицательна, траектория будет приближаться к началу координат, но не сможет пересечь окружность ρ=ρ (поскольку траектории не умеют пересекаться). Значит, она наматываться на эту окружность извне.
Здесь траектория не стремится к особой точке и не уходит на бесконечность, а приближается к другой, замкнутой траектории (предельному циклу). При 1=0 система не является структурно устойчивой. Например, особая точка, находящаяся в начале координат, при 1=0 является асимптотически устойчивой, а при любом положительном1 становится неустойчивой. Такие системы не могут быть орбитально топологически эквивалентными и значит при 1=0 происходит бифуркация. При 1=0 особая точка теряет устойчивость: была устойчивой (при 1≤0), а стала неустойчивой (при 1>0). Потеря устойчивости сопровождается рождением устойчивого предельного цикла, к которому стремятся все траектории, кроме самой особой точки.
Нелинейное отталкивание
Рассмотрим теперь случай 2>0. График правой части Ур.21 теперь является параболой, направленной ветвями вверх. Корень ρ положителен при 1<0. Предельный цикл, следовательно, существует тоже при 1<0. При этом траектории, стартующие ρ (0,ρ ) притягиваются к особой точке и отталкиваются от предельного цикла при увеличении t. При ρ>ρ траектории также отталкиваются от предельного цикла и уходят на бесконечность. При стремлении 1 к нулю предельный цикл уменьшается и схлопывается в точку.
При 1≥0 правая часть Ур.21 положительна для всех ρ>0 и траектории удаляются от особой точки.
Несмотря на сходство, между этими двумя сценариями есть существенное различие.
Пусть 2<0. Давайте представим себе, что мы следим за решением с каким-то конкретным начальным условием, выбранным наугад. При этом само решение нам доступно с некоторой погрешностью: в каждый момент времени мы видим положение точки в фазовом пространстве с небольшой случайной ошибкой. Несмотря на «дрожание» картинки мы всё-таки можем сделать какие-то качественные выводы о том, как меняется динамика при различных значениях. Мы видим, что при 1≤0 решение стремится куда-то к началу координат и там живет при t→+∞. Установившийся режим – небольшие случайные колебания, вызванные погрешностью нашего наблюдения, вокруг устойчивого положения равновесия. При небольших значениях 1>0 положение равновесия становится неустойчивым, но мы этого не заметим: траектория будет притягиваться к маленькому устойчивому предельному циклу, что будет соответствовать колебательному движению с небольшой амплитудой. Отличить такие маленькие колебания от случайного шума будет невозможно до тех пор, пока их амплитуда значимо не вырастет. Такой тип потери устойчивости называется мягкой потерей устойчивости. По отношению к бифуркации Андронова-Хопфа, происходящей по этому сценарию, используют также термин суперкритическая бифуркация.
Для 2>0 ситуация иная. При 1<0 предельное поведение нашей траектории существенно зависит от того, находится ли начальное условие внутри предельного цикла или вне него. В первом случае решение будет стремиться к началу координат и останется где-то там. А во втором случае оно уйдет куда-то на бесконечность. Никаких колебаний с

http://profbeckman.narod.ru/
малой амплитудой в этом случае мы не увидим (и с не малой тоже): предельный цикл неустойчивый и значит выбранная наугад траектория, будет от него быстро отдаляться с течением времени.
Если постепенно увеличивать 1, приближая его к нулю, при некотором значении предельный цикл пересечет наше начальное условие и траектория «резко» изменит свое предельное поведение. Говорят, что произойдёт «жёсткая» потеря устойчивости или субкритическая бифуркация Андронова-Хопфа.
Можно показать, что в «типичном случае» в однопараметрических семействах в фазовых пространствах любой размерности происходят только два типа локальных бифуркаций, которые мы сейчас рассмотрели: седлоузловая бифуркация и бифуркация Андронова-Хопфа. (Система уравнений (20) зависит от двух параметров, но нас интересует только один из них: при анализе бифуркации параметр 2 считался фиксированным.) Однако, уже для семейств с двумя параметрами ситуация становится гораздо более сложной.
Термины «мягкая» и «жёсткая» потери устойчивости связаны с описанием поведения системы с точки зрения «внешнего» наблюдателя, при медленной (в сравнении с динамикой системы) эволюции параметра системы и зашумлении системы малыми случайными возмущениями. В случае мягкой потери устойчивости решение перейдёт из положения равновесия (ставшего неустойчивым) в предельный цикл – наблюдатель будет видеть периодическое «дрожание» состояния системы недалеко от положения равновесия, которое будет усиливаться с ростом параметра. Однако, в масштабе времени «движения параметра», «отклонения» решения нарастают непрерывно. Напротив, при жёсткой потере устойчивости решение «резко» срывается и уходит за границу бассейна отталкивания исчезнувшего предельного цикла: с точки зрения наблюдателя, живущего в масштабе времени, в котором изменяется параметр, решение скачком поменяло режим.
Потеря устойчивости, происходящая при рождении цикла, называется мягкой, однако на практике это явление может приводить к катастрофическим последствиям. Один из наиболее известных примеров – колебания крыльев или хвостового оперения самолета при превышении скоростью набегающего потока некоторого критического (бифуркационного) значения. Это явление, называемое "флаттером" приводило к разрушению самолетов в конце 30-х годов XX в., когда их скорости достигли величин, достаточных для возникновения флаттера.
Пример бифуркации типа рождение предельного цикла из состояния равновесия - переход простейшего лампового генератора при соответствующем изменении управляющего напряжения от режима статических колебаний к автоколебательному режиму. В этом случае на фазовой плоскости из устойчивого фокуса в начале координат при коэффициенте затухания 0 рождается предельный цикл, амплитуда которого при
малых имеет порядок 
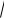 , а фокус становится неустойчивым. Бифуркация Хопфа может быть суперили субкритической.
, а фокус становится неустойчивым. Бифуркация Хопфа может быть суперили субкритической.
Суперкритическая (сверхкритическая, мягкая) бифуркация Хопфа – бифуркация,
имеющая место, если равновесная точка (0,0) – асимптотически стабильна при =0 (в точке бифуркации). В сверхкритической бифуркации Хопфа предельный цикл растет из точки равновесия прямо по параметрам бифуркации Хопфа: сначала предельный цикл имеет нулевую амплитуду, которая возрастает по мере дальнейшего перехода параметров в предельный цикл.
Субкритическая (докритическая, жёсткая) бифуркация – бифуркация, имеющая место, если равновесная точка (0,0) отрицательно асимптотически стабильна (при t ) когда =0. (Равновесная точка достигается при времени = 0, где ( 0)=0). В докритической бифуркации Хопфа существует неустойчивый предельный цикл, окружающий точку равновесия, и устойчивый предельный цикл, её окружающий. Нестабильный предельный цикл сжимается до точки равновесия, которая в ходе процесса
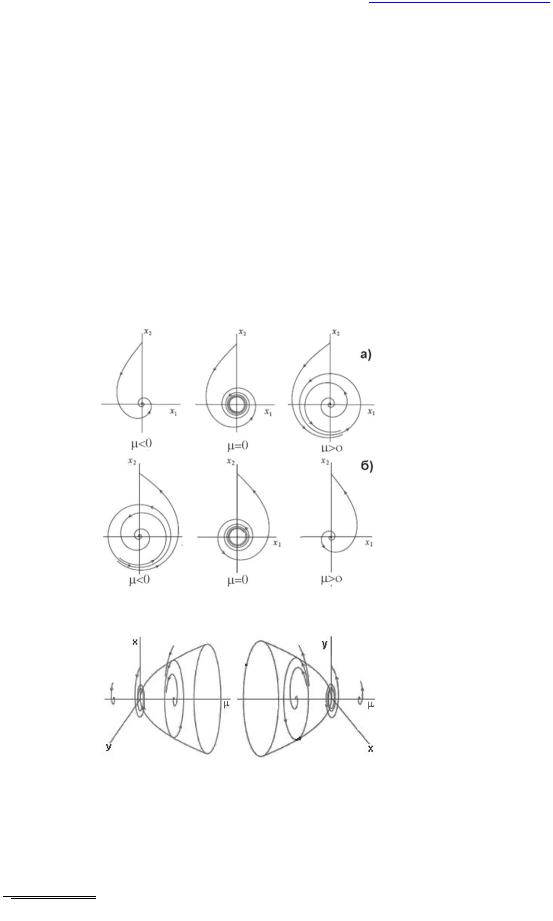
http://profbeckman.narod.ru/
становится неустойчивой. Для систем, запущенных вблизи точки равновесия, результатом является внезапное изменение поведения от подхода к устойчивому фокусу, к колебаниям большой амплитуды.
Мягкая бифуркация Андропова—Хопфа имеет место и в общем случае любой размерности пространства m>2 и даже в бесконечномерном случае. В случае жесткой бифуркации следует говорить об исчезновении седлового предельного цикла.
Рассмотрим простейший вариант суперкритической бифуркации Хопфа. Простейшая двумерная система, описывающая суперкритическую бифуркацию
Хопфа в полярных координатах, имеет вид
x y x x2 y2
y x y x2 y2
В полярных координатах это уравнение принимает форму r r( r2 )
1
r 0
(21)
(22а)
(22б)
Рис. 12. Фазовые портреты бифуркации Хопфа: а – суперкритическая, б – субкритическая.
Рис. 13. Бифуркации Хопфа: а – сверхкритическая бифуркация, отвечающая переходу от устойчивой спирали к колебаниям на предельном цикле; б – субкритическая бифуркация.
Из Ур.22б следует |
|
||
=t+t0. |
|
|
(23) |
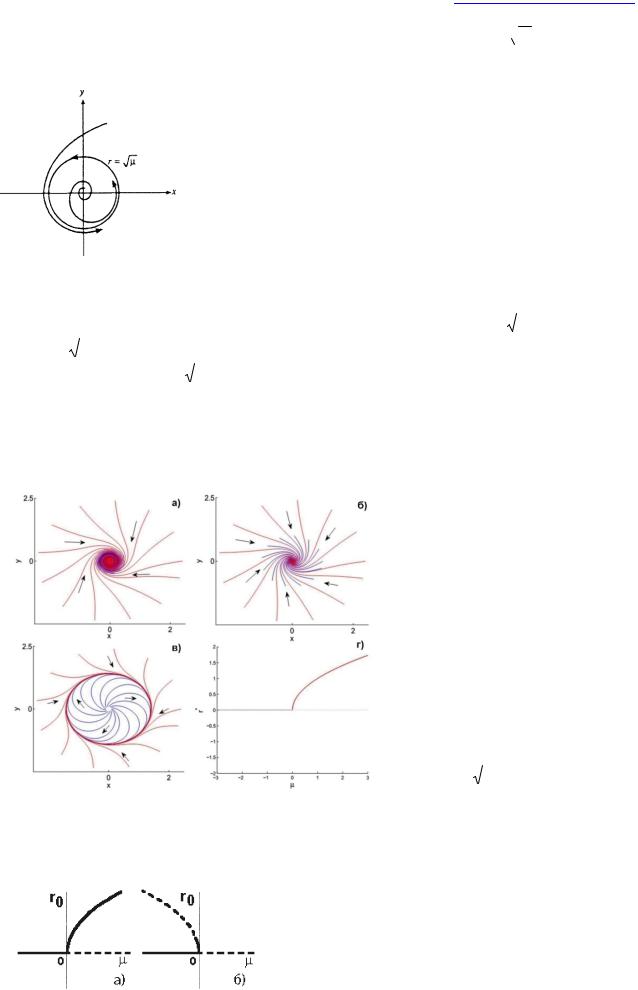
Если >0, то Ур.22а имеет решение |
|
||
= |
√ |
à |
(24) |
где t=0: r=r0.
http://profbeckman.narod.ru/
Ур.45 демонстрирует существование предельного цикла при r 
 , для >0 (рис. 13), с суперкритической бифуркацией вил (точка (0,0) – нестабильный фокус для >0.
, для >0 (рис. 13), с суперкритической бифуркацией вил (точка (0,0) – нестабильный фокус для >0.
Таким образом, при прохождении через точку =0, в начале координат происходят изменения от стабильного фокуса, через нестабильный фокус, с появлением нового периодического решения, бифурцирующего от =0.
Рис. 13. Предельный цикл для системы 2.68 для >0.
Единственной критической точкой этой системы r0=0, т.е. начало координат. Если 0 траектории движутся по часовой стрелке около точки r0=0. Если =0, то r r3 . Для ненулевого r имеем r 0 . Следовательно, здесь нет замкнутых орбит и все траектории сходятся к началу координат при t .
Начало координат - стабильный фокус (рис. 14а). Если <0, то -r2<0 для всех r. Как и в
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
предыдущем случае, r 0 для ненулевого значения r, здесь нет замкнутых орбит и начало |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
координат – стабильный фокус (рис. 14б). Если >0, то r 0 для r |
, и r 0 для |
||||||||||||||||||
r , |
|
. Начало |
координат |
– нестабильный фокус и, |
следовательно, |
имеет |
|||||||||||||
|
|||||||||||||||||||
стабильную орбиту r |
|
|
(рис. |
14в). В этом случае имеет место суперкритическая |
|||||||||||||||
|
|
||||||||||||||||||
бифуркация Хопфа при значении параметра =0 (рис. 14г). |
|
|
|
|
|
|
|
|
|
||||||||||
Несколько усложним исходную систему уравнений |
|
|
|
|
|
|
|
|
|
||||||||||
|
dr |
r r3 |
|
|
(25а) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
dt |
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
(25б) |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если (0) 0 так что ( ) не |
|||||||||
|
|
|
|
|
|
|
|
равно нулю в окрестности =0, то |
|||||||||||
|
|
|
|
|
|
|
|
Ур. 25 имеет две критические |
|||||||||||
|
|
|
|
|
|
|
|
точки r0=0 и |
r2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Рис. 15. Фазовые портрет |
|||||||||
|
|
|
|
|
|
|
|
суперкритической |
бифуркации |
||||||||||
|
|
|
|
|
|
|
|
Хопфа: а – =0, начало |
|||||||||||
|
|
|
|
|
|
|
|
координат – стабильный фокус; |
|||||||||||
|
|
|
|
|
|
|
|
б – =-0,5, начало координат – |
|||||||||||
|
|
|
|
|
|
|
|
стабильный |
|
|
фокус; в – =2, |
||||||||
|
|
|
|
|
|
|
|
начало |
|
|
координат |
– |
|||||||
|
|
|
|
|
|
|
|
нестабильный фокус, |
устойчивая |
||||||||||
|
|
|
|
|
|
|
|
орбита r |
|
|
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В случае сверхкритической бифуркации Хопфа при прохождении μ через точку бифуркации μ=0 ветвь r0=0 изменяется от устойчивого фокуса до неустойчивого фокуса и приводит к периодическому решению.
Рис. 16. Бифуркационная диаграмма бифуркации Хопфа: а – суперкритическая: б – субкритическая.
Однако при субкритической бифуркации Хопфа при изменении μ через точку бифуркации μ=0 ветвь r0=0 изменяется от устойчивого фокуса до неустойчивого фокуса, но не переходит в

http://profbeckman.narod.ru/
периодическое решение. Поэтому субкритические бифуркации Хопфа обеспечивают механизм возникновения хаоса (модель Лоренца, см. далее). В результате мягкой или суперкритической бифуркации Андронова—Хопфа происходит смена устойчивости особой точки, сопровождающаяся рождением из неё устойчивого предельного цикла, амплитуда которого пропорциональна √ , а период ≈ 2 / при μ 0.
Эта бифуркация играет важную роль в теории нелинейных систем дифференциальных уравнений как отправная точка различных каскадов бифуркаций перехода к хаосу.
Суперкритическая (сверхкритическая) бифуркация Хопфа – бифуркация, имеющая место, если равновесная точка (0,0) – асимптотически стабильна при =0 (в точке бифуркации). В сверхкритической бифуркации Хопфа предельный цикл растет из точки равновесия прямо по параметрам бифуркации Хопфа: сначала предельный цикл имеет нулевую амплитуду, которая возрастает по мере дальнейшего перехода параметров в предельный цикл.
Рис. 17. Два вида бифуркаций АндроноваХопфа на плоскости: а – суперкритическая; б – субкритическая.
Субкритическая (докритическая)
бифуркация – бифуркация имеет место, если равновесная точка (0,0) отрицательно асимптотически стабильна (при t ) когда=0. (Равновесная точка достигается при времени = 0, где ( 0)=0). В докритической бифуркации Хопфа существует неустойчивый предельный цикл, окружающий точку равновесия, и устойчивый предельный цикл, её окружающий. Нестабильный предельный цикл сжимается до точки равновесия, которая в ходе процесса становится неустойчивой. Для систем, запущенных вблизи точки равновесия, результатом является внезапное изменение
поведения от подхода к устойчивому фокусу, к колебаниям большой амплитуды.
Рис. 18. Бифуркация рождения цикла
Пример 10. В простейшем однопараметрическом случае бифуркация Андропова-Хопфа описывается системой уравнений:
x t x y x x2 y2
y t x y y x2 y2
В полярных координатах система имеет вид:
r t r r2
|
|
t 1 |
|
|
http://profbeckman.narod.ru/
Система имеет одно положение равновесия P(0; 0), которое является устойчивым фокусом, если 0 и устойчивый предельный цикл, если >0.
Представляет интерес изучение влияния параметра 2 на картину бифуркаций. Рассмотрим систему
x x x 2 x x2 y2 , |
|||||
|
(x |
2 |
y |
2 |
). |
y y y 2 |
|
|
|||
В полярных координатах система имеет вид:
|
r 2r |
2 |
|
r |
|
||
|
|
|
|
|
1 |
|
|
Уравнение 1 означает, что фазовая точка вращается с постоянной скоростью. Фазовый портрет первого уравнения
При 2<0 в случае отрицательного у исходной системы нуль является экспоненциально устойчивым фокусом. Когда обращается в нуль, начало координат продолжает оставаться устойчивым фокусом, правда, уже не экспоненциально устойчивым.
Когда становится положительным, начало координат теряет устойчивость и одновременно рождается малый предельный цикл динамической системы. Начало координат "передает" свою устойчивость этому циклу – он орбитально асимптотически устойчив. Амплитуда
отвечающего этому циклу решения пропорциональна 
 . При положительном значении
. При положительном значении
параметра 2 картина иная. При <0 начало координат представляет собой экспоненциально устойчивое положение равновесия, окруженное неустойчивым предельным циклом
(пропорционального 
 радиуса). При =0 этот цикл сливается с началом координат, опять же
радиуса). При =0 этот цикл сливается с началом координат, опять же
"передавая" ему свою неустойчивость, причем неустойчивость пока не экспоненциальная. Впоследствии, при >0, начало координат становится экспоненциально неустойчивым фокусом.
Вмногомерном случае соответствующая типичная бифуркация получается приписыванием
ксистеме (4) гиперболической системы. Один из примеров (отвечающий случаю 2<0) изображен на рис. 19.
Рис. 19. Бифуркация седло-узел в трехмерном случае.
Рис. 20. Бифуркация рождения инвариантного тора – бифуркация рождения цикла.
Бифуркация рождения цикла, отвечающая случаю 2<0, называется мягким возбкждением автоколебаний, сопровождающим потерю устойчивости стационарной точки, поскольку при возрастании параметра рождающийся цикл непрерывно зависит от. В противоположность этому, потеря устойчивости положения равновесия при 2>0
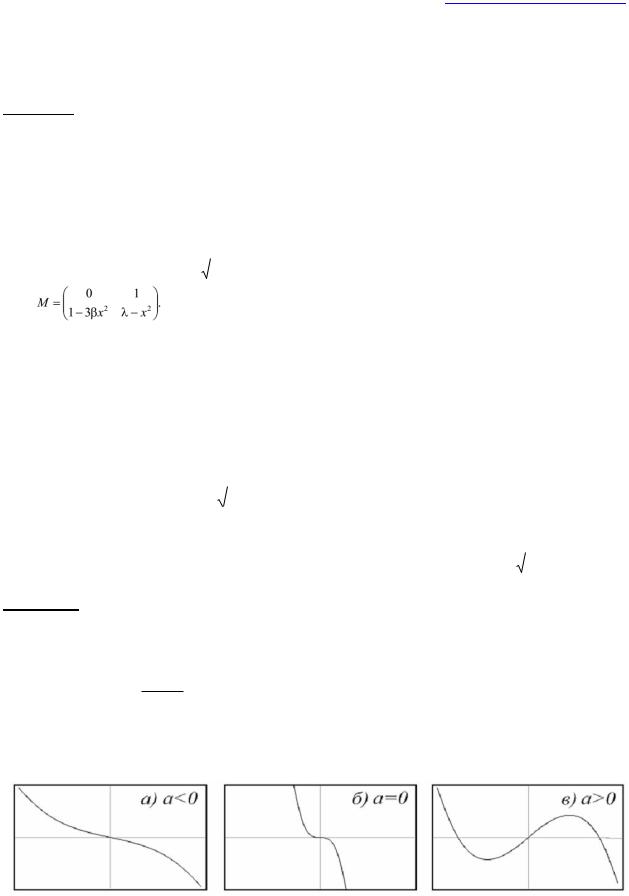
http://profbeckman.narod.ru/
называется жестким возбуждением системы, т. к. фазовая точка, находившаяся при <0 в окрестности устойчивого начала координат, при >0 быстро "выбрасывается" из окрестности стационарной точки (например в окрестность имеющейся у системы удаленной устойчивой стационарной точки или удаленного устойчивого цикла).
Пример 11. Найти бифуркацию Андронова-Хопфа в модификации уравнения ван-дер-Поля
x x2 x x x3 0
Исследовать все возможные неподвижные точки. Перепишем это уравнение в стандартной форме: x y, y ( x2 )y x x3
Найдем неподвижные точки рассматриваемой системы. Для этого приравняем нулю производные по времени и решим полученные уравнения. Тогда получаем, что система имеет три неподвижных
точки (y=0, x=0) и (y= 0, |
x |
1 |
|
). Выпишем теперь матрицу линеаризации системы. Она имеет |
|
|
|
|
|||
|
|
||||
|
|
|
|
|
|
вид: |
Соответственно, след и якобиан этой матрицы будут |
||||
S= -x2, J=-1+3 x2
Известно, что условие для нахождения бифуркации Андронова-Хопфа имеет следующий вид:
S=0, J>0.
Для определения в каких неподвижных точках рассматриваемой системы наблюдается бифуркация Андронова – Хопфа начнем с первой неподвижной точки (y=0, x=0). След и якобиан для этой неподвижной точки будут: S= , J=-1. Поскольку якобиан отрицательный, то условие бифуркации АндроноваХопфа выполнено быть не может. Соответственно для этой неподвижной точки бифуркация Андронова-Хопфа не наблюдается. Теперь рассмотрим две оставшиеся
неподвижные точки (y= 0, x |
1 |
|
). Для них получаем S= -1/ , J=2. Из полученных равенств |
||||||
|
|
|
|||||||
|
|||||||||
|
|
|
|
|
|
|
|
||
следует, что условие J>0 выполняется всегда. Следовательно, надо проверить выполнение условия |
|||||||||
S =0. Приравнивая нулю след, находим, что для неподвижных точек (y= 0, x |
1 |
|
) бифуркация |
||||||
|
|
|
|||||||
|
|||||||||
Андронова-Хопфа происходит при выполнении условия: =1/ .
Пример 12. Найти бифуркации седло-узел Андронова-Хопфа и их общую точку (бифуркацию Богданова-Такенса) для автоколебательного осциллятора Богданова-Такенса:
x x x a x2 0.
Уравнение осциллятора может быть переписано в следующем виде
x x x U(x) 0x
где потенциал задан кубическим полиномом, показанным на рис. 21. Таким образом, в системе должна иметь место бифуркация седло-узел, отвечающая слиянию максимума и минимума потенциала. С другой стороны, при >0 осциллятор характеризуется отрицательным трением, т.е. имеются предпосылки для возникновения автоколебаний и бифуркации Андронова-Хопфа
Рис. 21. Вид потенциала U(x).
Проведем соответствующий бифуркационный анализ. Перепишем уравнение осциллятора Богданова-Такенса в стандартной форме:
̇= , ̇= ( − ) − +
|
0 |
http://profbeckman.narod.ru/ |
и запишем для него матрицу линеаризации: |
1 |
Неподвижные точки этой системы находятся их условия равенства нулю производных от времени |
|
= − + 2 |
− |
динамических переменных x и y. Осциллятор Богданова-Такенса имеет две неподвижные точки
x a, |
y 0. Первая из них (отвечающая знаку +), в соответствии с рис.6в, неустойчива, а |
|||||||
вторая – устойчива. Для последней тогда имеем |
0 |
1 |
||||||
Находим далее след и якобиан этой матрицы. Они |
равны: |
+ |
||||||
= −2 |
||||||||
S |
|
|
; |
J 2 |
|
|
√ √ |
|
|
a |
a |
|
|||||
Условием бифуркации седло-узел является обращение в ноль якобиана матрицы М. Это условие выполняется при a=0. Условия на бифуркацию Андронова-Хопфа имеют следующий вид S=0, J>0.
Поэтому бифуркация Андронова – Хопфа имеет место при 
 а
а
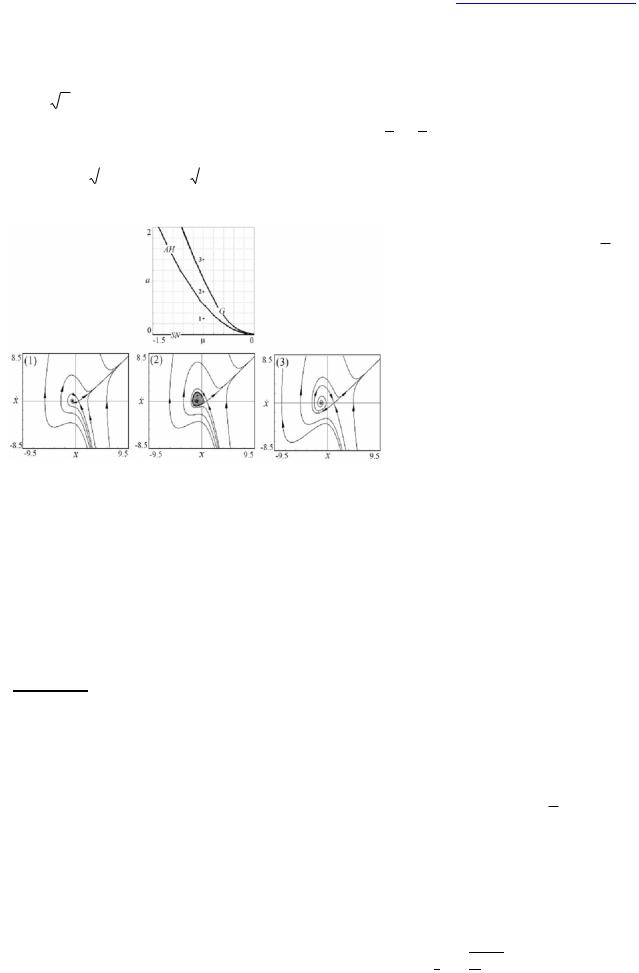
Рис. 22. Бифуркационные линии осциллятора в окрестности точки Богданова-Такенса BT на плоскости параметров (μ, a),( и фазовые портреты в характерных точках, AH – линия бифуркации Андронова-Хопфа, SN
– линия бифуркации седло-узел, G
– линия влипания предельного цикла в петлю сепаратрисы.
При этом условие положительности якобиана выполняется при любых значениях параметра a. Теперь найдем общую точку обеих бифуркаций. Для этого положим a =0. Тогда получим, что . Таким образом, общая точка двух бифуркаций, отвечающая бифуркации Богданова-Такенса, на плоскости параметров имеет координаты μ=0. Таким образом, общая точка двух бифуркаций, отвечающая бифуркации Богданова-Такенса, на плоскости параметров имеет координаты μ=a=0 . В этой точке обращаются в ноль одновременно и след, и якобиан линеаризованной матрицы, что может служить удобным приемом при определении точек Богданова-Такенса в конкретных системах. На рис. 22 показаны линии основных бифуркаций коразмерности один в окрестности точки бифуркации БогдановаТакенса и фазовые портреты системы в избранных точках. Можно видеть характерные для точки Богданова-Такенса метаморфозы фазового портрета системы. Отметим, что наряду с описанными локальными бифуркациями для такой системы оказывается типичной и нелокальная бифуркация влипания предельного цикла в петлю сепаратрисы.
Пример 13. Дискретный осциллятор Богданова-Такенса описывается отображением: xn 1 xn yn 1 , yn 1 yn xn yn a xn2 .
Провести полный анализ бифуркаций устойчивой неподвижной точки этого отображения; построить карту динамических режимов этого отображения и указать на ней характерные линии и точки бифуркаций; сопоставить свойства этого отображения и исходной потоковой системыпрототипа. Найдём неподвижные точки этого отображения. Они находятся из условия xn+1=xn, и yn+1=yn]. Тогда из формул (6) следует что x=x+ y; y=y+ [( -x)y-a+x2 Решим последние уравнения и
получим, что рассматриваемое отображение имеет две неподвижные точки x 
 a и y=0. При этом одна из них будет устойчивой, а вторая неустойчивой. Выпишем теперь матрицу возмущений
a и y=0. При этом одна из них будет устойчивой, а вторая неустойчивой. Выпишем теперь матрицу возмущений
(матрицу |
монодромии) |
( |
для |
|
исходного |
отображения. |
Она |
имеет |
вид: |
||||
= |
1 + |
(− + 2 ) |
) |
1 + |
− |
) . |
Далее запишем след и якобиан этой матрицы |
S=2+ ( - |
|||||
|
(− + 2 |
+ |
( |
− |
) |
|
|||||||
x)+ 2(2x-y), J=1+ ( -x). Для определения устойчивости неподвижных точек двумерного отображения и нахождения их бифуркаций необходимо знать собственные числа матрицы монодромии (мультипликаторы). Из свойств матрицы 2×2 известно, что собственные числа
подчиняются соотношению 2-S +J=0. Откуда следует, что , = |
− |
