http://profbeckman.narod.ru/

Интегральной кривой системы дифференциальных уравнений х F(x,t) называется график ее решения, а фазовой кривой - проекция интегральной кривой на фазовое пространство вдоль оси t. Примеры интегральных и фазовых кривых (траеторий) изображены на рис. 7.

Теорема. Через каждую точку расширенного фазового пространства дифференцируемого векторного поля проходит одна и только одна интегральная кривая с системы дифференциальных уравнений (22) с вещественным временем.

Задание начального условия в начальный момент времени х(0)=x0 однозначно определяет решение системы дифференциальных уравнений в любой момент времени t:

( ) = ( ). Задача нахождения решения системы дифференциальных уравнений, удовлетворяющего заданному начальному условию, называется задачей Коши, Отображение φt является отображением фазового пространства Μ в себя и называется фазовым потоком. Любая область G фазового пространства под воздействием фазового потока переходит за время t в некоторую другую область Gt=φt(G).

10.3 Линейные ОДУ на плоскости

Фазовые плоскости возникают в двумерных автономных ОДУ, записаны в виде

Здесь f1 и f2 - функции. Эти две переменные могут описывать, например, положение и скорость частицы, состояние системы хищник-жертва или концентрации двух реагентов в гомогенной химической реакции.

Если x(t), y(t) - решение системы, то в каждый момент времени t=p, x(p), y(p) определяет точку в фазовой плоскости. Точка изменяется со временем, поэтому все решения, x(t), y(t), прослеживает кривую или траекторию в фазовой плоскости.

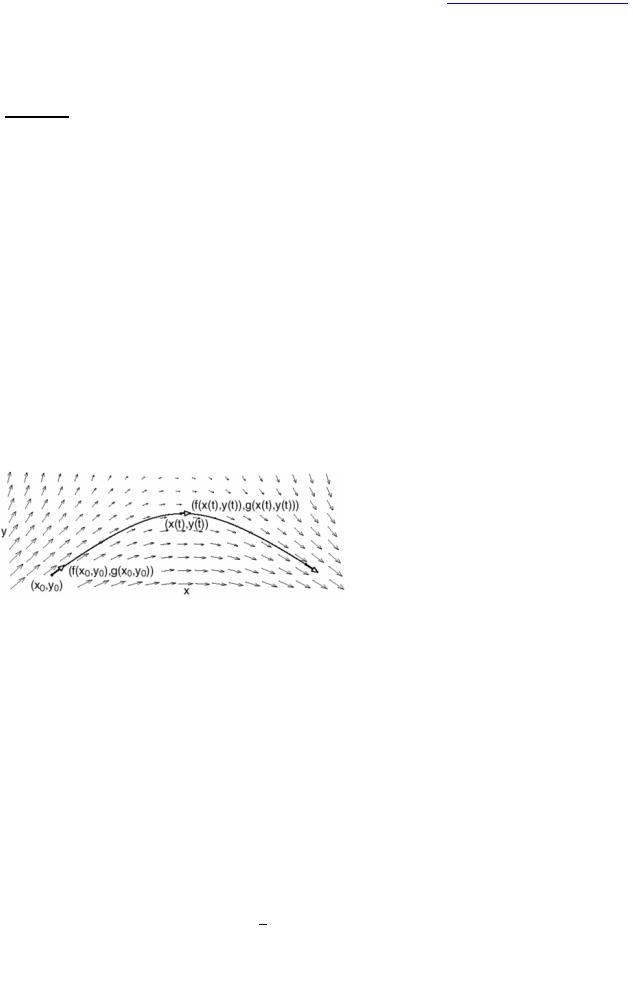
Рис. 8. Фазовая плоскость. Правая часть двумерной динамической системы определяла векторное поле.

Решения уравнений определяют кривые или траектории в фазовой плоскости. Векторное поле всегда указывает направление движения траекторий.

Конечно, не каждая произвольная кривая на фазовой плоскости представляет собой решение уравнения. Особенность траекторий решения заключается в том, что вектор скорости в каждой точке вдоль траектории задается правой частью указанного выше дифференциального уравнения. То есть вектор скорости траектории x(t), y(t) в точке x(p), y(p) задается формулой (x', y') = (f1(x(p), y(p)), f2(x(p), y(p)). Важное геометрическое свойство - вектор f1(x, y), f2(x, y) всегда указывает в направлении потока решения - полностью характеризует траектории решения (рассматриваемые как подмножества фазового пространства). Функция, которая присваивает (f1(x, y), f2(x, y)) к (x, y) называется векторным полем.

Двумерные фазовые пространства возникают также в дискретных динамических системах вида xt+1=f1(xt,yt); yt+1=f2(xt,yt). В общем случае, как и в случае непрерывного времени, фазовое пространство может быть подмножеством R2 или любой поверхностью с границей или без неё.

Точки равновесия двумерной динамической системы – это где f1=0 и f2=0. Заметим, что если (x0, y0) является равновесием, то ((x(t), y(t)))=(x0, y0) для всех времен является (постоянным) решением системы. Равновесие может быть как устойчивым, так и неустойчивым.

Непостоянное решение ((x(t), y(t)) динамической системы является периодическим если ((x(0), y(0))=(x(T), y(T))) для некоторого (Т>0) Минимальный Т, удовлетворяющий этому требованию, называется периодом. Поскольку ((x(t), y(t))=(x(t+T), y(t+T))) для всех t, периодическое решение соответствует замкнутой кривой в фазовой плоскости.

http://profbeckman.narod.ru/

Периодические решения могут быть устойчивыми или неустойчивыми. Грубо говоря, периодическое решение устойчиво, если решения, начинающиеся вблизи замкнутой кривой, остаются близкими для всех t>0 (это соответствует орбитальной устойчивости периодической орбиты).

Обычно гораздо труднее найти периодические решения, чем найти равновесия. Точка равновесия ((x0, y0)) удовлетворяет уравнениям (f1(x0, y0)=f2(x0, y0)=0), и эти уравнения обычно можно решить с помощью простых численных методов. Мы также отмечаем, что равновесие является локальным объектом - это просто одна точка в фазовом пространстве. Колебания или периодические орбиты являются глобальными объектами; они соответствуют целой кривой в фазовом пространстве, которая восстанавливается. Эта кривая может быть довольно сложной.

Систему ОДУ обычно решают матричным методом.

На всякий случай сначала напомним некоторые элементы линейной алгебры. Задача на собственные значения матрицы формулируется следующим образом. Пусть A- квадратная матрица n-го порядка, X – вектор-столбец, λ – число.

собственным вектором матрицы A, если существует такое ненулевое число , что

Число при этом называется собственным значением вектора X относительно матрицы А, соответствующий собственному вектору Х. Совокупность всех собственных значений называется спектром матрицы A.

Замечание. В более общем виде используется следующий алгоритм вычисления собственного значения для матрицы. Если задана n×n квадратная матрица A над вещественными или комплексными числами, собственное значение λ и соответствующий ему корневой вектор Х – это пара, удовлетворяющая равенству: (A−λEn)kХ=0, где: Х – ненулевой n×1 вектор-столбец, En – единичная матрица n×n, k – положительное целое число, λ и X могут быть комплексными, даже если A вещественна. Если k=1, вектор v просто называется собственным вектором. В этом случае: AX=λX.

Матричное уравнение (24) представляет собой однородную систему линейных алгебраических уравнений относительно вектора X:

(A-λEn)X=0, (25)

где Еn - единичная матрица.

Единичная матрица – квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю. Единичная матрица раз мера nxn обозначается En

Матрица A- En – характеристическая матрица матрицы A, многочлен |A- En| –

характеристический многочлен матрицы A, уравнение |A- En|=0 называется характеристическим уравнением матрицы A.

Собственными числами матрицы А являются корни характеристического уравнения |A- En|=0 и только они. Координаты собственного вектора Х соответствующего собственному значению находятся из однородной системы уравнений

http://profbeckman.narod.ru/

Собственный вектор – понятие в линейной алгебре, определяемое для квадратной матрицы как вектор, умножение матрицы на который даёт коллинеарный вектор – тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом (собственных значением) матрицы. Одному собственному значению может соответствовать несколько (линейно независимых) собственных векторов, в таком случае говорят о собственном подпространстве для данного собственного значения.

Собственный вектор матрицы A – ненулевой вектор u , который при умножении на некоторую квадратную матрицу A превращается в самого же себя с числовым коэффициентом ( Аu u ). Число – собственное значение (собственное число) данной матрицы. Собственный вектор u соответствует собственному значению .

Определитель линейного оператора А - detА, многочлен относительно , называется характеристическим многочленом оператора А. Он не зависит от выбора базиса. Необходимое и достаточное условие разрешимости системы (24) описывается уравнением

det(A-En)=0, (27)

которое называется характеристическим (или вековым) уравнением оператора А задачи на собственные значения.

Для того чтобы число было собственным значением оператора А, необходимо и достаточно, чтобы это число было корнем характеристического оператора А. Существует хотя бы один собственный вектор, соответствующий каждому собственному значению λ.

Рассмотрение поведения динамической системы на двумерной фазовой плоскости начнём с системы двух линейных обыкновенных дифференциальных уравнений с постоянными коэффициентами

Двумерная система линейных дифференциальных уравнений имеет вид

Эта система может быть решена аналитически путём интегрирования

(29)

Если трактовать переменную t как время, то решение x=x(t), y=y(t) описывает закон движения точки (x;y) на плоскости x0y, называемой фазовой плоскостью. Кривая, по которой движется точка, называется траекторией, а уравнения x=x(t), y=y(t) задают параметризацию этой кривой.

При равновесии, система (28) переходит в систему:ax by 0

cx dy 0 (30)

Систему (28) можно преобразовать в матричную форму

http://profbeckman.narod.ru/

или

где С1 и С2 – произвольные константы.

Собственные значения – это показатели степени экспонент, а собственные векторы

– коэффициенты. Если решения записываются в алгебраической форме, они выражают фундаментальный мультипликативный множитель экспоненциального члена. Из-за неединственности собственных векторов каждое полученное таким образом решение имеет неопределенные константы С1, С2,...Сn.

В общем решение есть

(42)

где λ1 и λ2 – собственные значения, а (u11, u21), (u12, u22) – основные собственные векторы. Константы C1 и C2 учитывают неединственность собственных векторов и не

разрешимы, если для системы не задано начальное условие.

В практических заданиях сначала разыскиваются собственные значения и только потом собственные векторы. У квадратной матрицы размером nxn существует ровно n собственных значений, причём некоторые из них (или даже все) могут быть кратными (совпавшими). некоторые или все собственные значения могут быть комплексными. Каждому собственному значению соответствует хотя бы один собственный вектор, и если все собственные числа матрицы A различны, то она имеет ровно n собственных векторов.

Обычно классификацию положений равновесия линейной системы, основанную на собственных значениях. Однако тип точки равновесия можно определить и без вычисления собственных значений 1, 2, а зная лишь только определитель матрицы detA и её след trA.

Собственные значения матрицы – все корни характеристического уравнения.

Здесь V1 и V2 – корни уравнения bV 2 (d a)V c 0.

Сейчас будем рассматривать только случаи, когда характеристические корни 1, 2 не равны нулю и, следовательно, bc-ad 0. соответствующие критические точки называются особыми точками первого порядка или элементарными точками.

Собственные значения 1 и 2 линейного оператора А находят путём решения характеристического уравнения. Они равны

http://profbeckman.narod.ru/

где дискриминант этого квадратного уравнения определяется соотношением, D=(trA)2−4detA, где trA – след матрицы, а =detA – определитель матрицы А.

В зависимости от знака подкоренного выражения (a+d)2-4(ad−bc) корни характеристического уравнения могут принимать как действительные, так и комплексные значения. От этих значений зависит то, как будет выглядеть фазовый портрет системы.

элементы. Приравниваем соответствующие элементы векторов-столбцов и получаем однородную

Это характеристическое уравнение матрицы А, корни которого являются собственными числами данной матрицы. Сначала найдём собственные значения. Составим характеристическое

2=3, каждому из них соответствует свой собственный вектор. Рассмотрим собственное число1=2 и подставим значение = 1=2 в однородную систему уравнений

следует подобрать у так, чтобы х-координата собственного вектора была целой, положительной и

2

минимальной. Пусть у=-1, тогда х=-2 (-1)=2 и u .

1 1

http://profbeckman.narod.ru/

Вычислим собственные значения λi матрицы A, составленной из коэффициентов заданных уравнений:

2 5

13, 2 3

12

Вданном примере характеристическое уравнение имеет два различных действительных корня. Найдем собственный вектор V1, соответствующий собственному числу λ1=3. Подставляя λ1=3,

получаем векторно-матричное уравнение для определения V1: (A−λEn)V1=0. Пусть собственный

вектор V1 имеет координаты V1=(V11,V21)T (здесь индекс T означает операцию транспонирования). Тогда предыдущее уравнение можно записать в виде:A I 2

После перемножения матриц получаем систему двух уравнений:

Оба уравнения являются линейно зависимыми. Из второго уравнения находим соотношение между координатами собственного вектора: V11=V21. Полагаем V21=1. Следовательно, V11=1. Таким образом, собственный вектор V1 имеет координаты V1=(1,1)T. Аналогично определяем 2-ой собственный вектор V2, соответствующий λ2=−3. Пусть V2=(V21,V22)T. Тогда

Получаем систему двух одинаковых уравнений:

V21 5V22 0

V21 5V22 0

http://profbeckman.narod.ru/

Рис. 9. Траектории в задаче 1 (собственные значения одного знака).

На рис. 26а, б изображены траектории рассматриваемой системы в случае ( 1 2>0. Стрелками указано направление движения точки при возрастании параметра t. Такую картину траекторий и точку (0;0) называют узлом. В случае 1>0, 2>0 узел называется неустойчивым (рис.26а), в случае 1<0, <0 – устойчивым (рис. 26б). Точная формулировка понятия устойчивости будет дана позднее, сейчас же нам достаточно того, что в первом случае точки, отличные от (0;0), с ростом времени удаляются от начала координат, а во втором случае – притягиваются к нему. В частном случае 1= 2 все траектории, отличные от положения равновесия, являются лучами. Такая картина траекторий называется дикритической или звёздным узлом (рис.27, 26).

гипербола с асимптотами x=0 и y=0. На рис.28 изображены траектории в случае 1<0< 2. При движении по траектории y=0 (x>0 или x<0) точка приближается к началу координат. При движении по остальным траекториям при t + точка удаляется от точки покоя. В такой ситуации точка (0;0) называется седлом.

Рис. 10. Траектории в задаче 1 (равные собственные значения.

Пример 13. Найти траектории системы

Решение этого уравнения =ln . Можно построить график функции x=x(y). В точке

(0;0) все траектории касаются оси Ох. Определить направление движения по траектории можно из первого уравнения системы: в точке (х;0) вектор скорости

далее): устойчивым, если <0, и неустойчивым, если >0.

Рис. 11. Траектории в задаче 2 (собственные значения разных знаков).

Рис. 12. Траектории в задаче 2.

Задача 3. Нарисовать траектории системы

http://profbeckman.narod.ru/

комплексно-сопряжённых корня 1,2= +i . Перейдём в полярную систему координат, положив x= cos , y= sin . Тогда решение - 2d = d . При =0 имеем точку покоя (0;0). Если же >0, то

d Ce . d

Траектории, соответствующие этим решениям являются спиралями. Если / >0, то с ростом расстояние от точки на траектории до начала координат уменьшается, т.е. спираль сужается при движении по ней в направлении против часовой стрелки. Если / <0, то спираль расширяется.

Рис. 13. Траектории в задаче 3.

Рис. 14. Траектории в задаче 4.

Решение системы можно записать через матричную экспоненту

Это позволяет определить направление движения точки при возрастании параметра t. Множитель e t показывает, что точка (x;y), двигаясь по траектории, с ростом t удаляется от положения равновесия, если >0, и приближается к нему, если <0. На рис.90(a–d) изображены траектории системы при различных значениях и . Точка (0;0) – фокус, устойчивый, если <0, или неустойчивый, если >0.

Пример 14. Найти фазовые траектории системы уравнений