http://profbeckman.narod.ru/

имеет решение x=sint; x=соst также является решением этого уравнения. Функция х(t)=с1sint+с2cost

– решение Ур. 11 при любых с1 и с2. Для выбора конкретного решения необходимы дополнительные условия. Найдем, например, решение Ур. 11, проходящее через точку x(0) 1, x(0) 3 . Подставляя эти значения в общее решение, получим 1=с1sin0+c2cos, 3=c1cos0- c2sin0. Отсюда с1=3, с2=1, т. е. искомое решение имеет вид х=3sint+cost.

Рассмотрим аналитические методы решения линейного дифференциального уравнения n-го порядка. Одним из наиболее распространенных является метод, основанный на нахождении корней характеристического полинома. Пусть дано однородное линейное дифференциальное уравнение с постоянными коэффициентами и начальными условиями

Таким образом, для получения аналитического решения требуется:

–записать характеристическое уравнение;

–определить его корни p1, …, pn;

–найти общее решение Ур. 13;

–используя начальные условия, определить значения коэффициентов с1, …, сn.

Для однородного линейного уравнения с постоянными коэффициентами p0y(n)+p1y(n-1)+...+pny=0

характеристическим уравнениям является уравнение p0 n+p1 (n-1)+...+pn=0

Пример 3. Решить дифференциальное уравнение

y′′′+2y′′−y′−2y=0.

Составим соответствующее характеристическое уравнение:λ3+2λ2−λ−2=0. Решая его, находим корни:λ2(λ+2)−(λ+2)=0, (λ+2)(λ2−1)=0, (λ+2)(λ−1)(λ+1)=0, λ1=-2, λ2=1, λ3=-1. Видно, что все три

корня действительные. Поэтому, общее решение дифференциального уравнения записывается в виде y(x)=C1e−2x+C2ex+C3e−x, где C1,C2,C3 − произвольные постоянные.

10.2 Фазовое пространство и пространство состояний

Изменение состояний динамической системы во времени представляет собой движение в пространстве состояний. Пространство состояний играет важную роль в теории управления, применяется оно и в динамике под названием фазовое пространство.

Замечание. Обычно пространство состояний и фазовым пространство динамической системы считают синонимами, но чаще пространство состояний встречается не при описании систем с непрерывным временем, а теории дискретных систем, в которых пространство состояний представляет собой набор значений принимаемых процессом.

Пространство состояний - совокупность всех возможных состояний динамической системы; каждому состоянию системы соответствует уникальная точка в пространстве состояний.

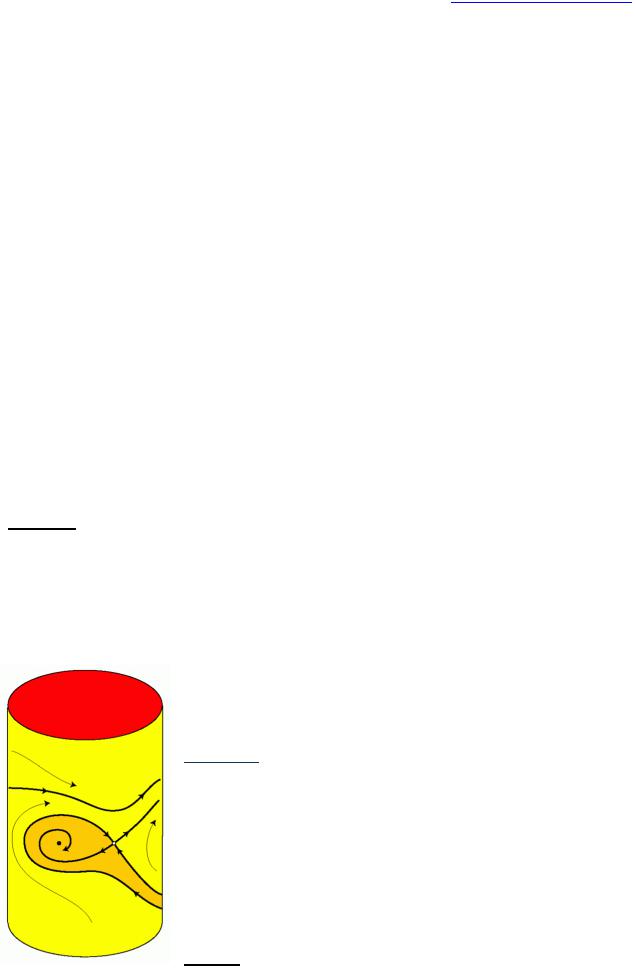
Рис. 2: Пространство состояний затухающего маятника с крутящим моментом.

Пример. Состояние маятника однозначно определяется его углом и

http://profbeckman.narod.ru/

угловой скоростью, поэтому пространство состояний представляет собой совокупность всех возможных пар «(угол, скорость)», которые образуют цилиндр (S1хR), как на рис. 2.

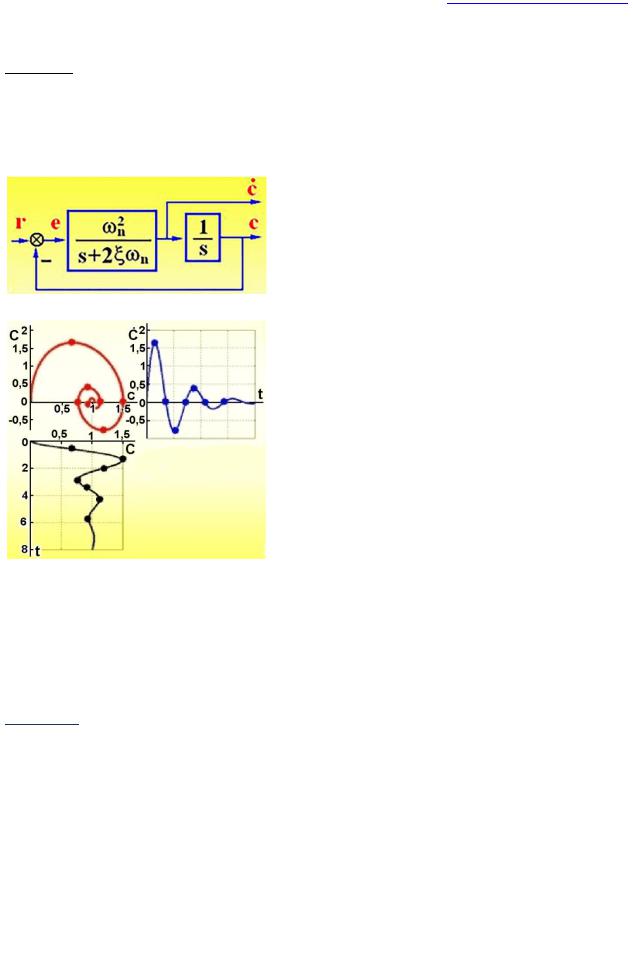
Пример 4. Элемент электрической схемы с обратной связью. Схема – на рис. 3, фазовый портрет

– на рис. 4. Система уравнений

r(t)=1(t)

Рис. 3. Схема с обратной связью.

Рис. 4. Фазовый портрет системы с обратной связью.

В принципе, любой абстрактный набор параметров может быть пространством состояний конкретной динамической системы. Пространство состояний может быть конечным, состоящим всего из нескольких точек, но может быть конечномерным, состоящим из бесконечного числа точек, образующих гладкое многообразие. Это типично для ОДУ и отображений. Именно такое пространство состояний называют фазовым пространством. Пространство состояний может быть бесконечномерным, например, в уравнениях с частными производными, а в символической динамике - это канторово множество, которое нульмерно.

Замечание. Согласно самому абстрактному определению динамическая система – гомоморфизм абелевой группы всех автоморфизмов. Пространство Х является пространством состояний динамической системы по определению. Это может быть любое пространство с любой топологией или вообще без топологии; оно может быть конечным или бесконечным.

Идеи фазового пространства и фазовой плоскости, пространство состояний, фазовый портрет, фазовые траектории, особые точки и т.п. широко используются при наглядном представлении решений обыкновенных дифференциальных уравнений, описывающих состояние динамической системы.

Пространство состояний – конечномерное пространство, которому принадлежит вектор состояния обыкновенного дифференциального уравнения в форме Коши.

Линеаризация – выделение из векторного дифференциального уравнения в форме Коши линейной части с помощью матриц Якоби (производных Фреше) при малых отклонениях относительно выбранной (номинальной, рабочей) траектории «вход – состояние».

http://profbeckman.narod.ru/

Переходная матрица состояния – фундаментальная матрица решений векторного линейного однородного дифференциального уравнения с переменными коэффициентами, которая позволяет перейти из начального состояния в любое другое в пространстве состояние.

Идеи фазового пространства стали использоваться в классической и статистической механике в последней трети 19-го века. Есть указания на то, что первым этот термин употребил французский математик Ж. Лиувилль в 1838 г. Сама концепция фазового пространства была разработана в конце 19 века Л. Больцманом, А.Пуанкаре и У.Гиббсом применительно к задачам физической статистики, линейной и нелинейной динамики.

Состояние сколь угодно сложной системы представляется в фазовом пространстве единственной точкой, а эволюция этой системы – перемещением этой точки. Фазовое пространство динамической системы представляет собой пространство, в котором представлены все возможные состояния системы, причём каждое возможное состояние соответствует одной единственной точке в фазовом пространстве. Траекторию движения изображающей точки в этом пространстве называют фазовой траекторией.

В классической механике движение изображающей точки определяется уравнениями Гамильтона, описывающими поведение сложных систем в фазовом пространстве гладких многообразий.

Уравнения Гамильтона (канонические уравнения) в физике и математике – система дифференциальных уравнений:

где точкой над p и q обозначена производная по времени. Система состоит из 2N дифференциальных уравнений первого порядка (j=1, 2,…, N) для динамической системы, описываемой N (обобщёнными) координатами, являющихся уравнения движения (одной из форм таких уравнений, наравне с уравнениями Лагранжа, являющейся обобщением ньютоновских уравнений движения) системы, где H=H(q,p,t) H(q1,q2,...,qN, p1,p2,...,pN,t) – так называемая функция Гамильтона, также иногда именуемая гамильтонианом, t — врем, qi – (обобщенные) координаты q1,q2,...,qN, и pi – обобщённые импульсы (p1,p2,...,pN) определяющие состояние системы (точку фазового пространства).

Напомним, что в классической механике фазовое пространство является пространством всех возможных состояний системы. Состояние механической системы определяется составляющими импульсами p и координатами q, которые вместе определяют будущее поведение этой системы. Если известны значения p и q в момент времени t, можно вычислить p и q в момент времени t+1, используя теоремы классической механики, математическую базу которых и составляют уравнения Гамильтона.

Для описания движения отдельной частицы вам необходимы 6 переменных: 3 координаты и 3 импульса, т.е. 6-ти мерное пространство. Каждая точка в этом 6-мерном пространстве характеризует состояние частицы, конечно же ограниченное законами классической механики. Для описания системы из N частиц используется 6N-мерное фазовое пространство.

В простом случае гамильтониан H представляет энергию физической системы, которая есть сумма кинетической и потенциальной энергий. В случае механических систем это пространство чётной размерности, координатами в котором являются обычные пространственные координаты и их импульсы. Например, фазовое пространство для системы, состоящей из одной свободной материальной точки, имеет 6 измерений: 3 обычные координаты и 3 – компоненты импульса. Фазовое пространство для системы из двух свободных материальных точек содержит 12 измерений и т.д.

Пример 5. Простой маятник состоит из стержня, вращающегося в одной плоскости вокруг гвоздя, вбитого в стену. Он полностью описывается одной координатой и одним импульсом. Его импульс

http://profbeckman.narod.ru/

равен нулю в верхней части и максимум внизу. Его положение определяется углом и изменяется между плюсом/минусом . Если построить состояния p и в декартовой системе координат, то получим эллипсоид (или, если подобраны адекватные координаты, круг), который полностью описывает все возможные состояния маятника.

Вквантовой механике термин фаза так же используется: он относится к сложной фазе комплексных чисел, волновые функции которой принимают значения в. В квантовой механике координаты p и q фазового пространства обычно становятся операторами в гильбертовом пространстве. Квантовомеханическое состояние не обязательно имеет чётко определенную координату или чётко определенный импульс (и никогда не может иметь обоих в соответствии с принципом неопределенности Гейзенберга). Понятие фазового пространства и гамильтониана H можно рассматривать как важную связь между тем, что в противном случае выглядит как две очень разные теории. Состояние теперь не является точкой в фазовом пространстве, а представляет собой комплекснозначную волновую функцию. Гамильтониан H становится оператором и описывает наблюдаемую величину.

Втеории динамических систем фазовое пространство является более общим понятием, чем в механике. Оно не обязательно чётномерно и динамика в нём не обязательно задаётся уравнениями Гамильтона. Решение уравнений Гамильтона pi(t), qi(t), i=1, N определяет траекторию в объединенном 2N-мерном пространстве обобщенных координат и импульсов, называемых фазовым пространством системы. В физике фазовое пространство представляет собой концепцию, которая объединяет классическую (гамильтоновскую) механику и квантовая механика; в математике фазовое пространство - это концепция, которая объединяет симплектическая геометрия с гармоническим анализом решений дифференциальных уравнений в частных производных.

Симплектическая геометрия – область дифференциальной геометрии и дифференциальной топологии, изучающая симплектические многообразия: гладкие многообразия с выбранной замкнутой невырожденной 2-формой. Исходно симплектическая геометрия возникла из гамильтонова формализма в классической механике, когда фазовое пространство для классической системы оказывалось симплектическим многообразием.

Фазовое пространство в теории динамических системе – абстрактное пространство, ассоциированное с конкретной динамической системой, точки в котором однозначно характеризуют все возможные состояния данной системы. Предполагается, что это пространство снабжено естественным определением меры (расстояний, площадей и т.д.).

Фазовое пространство – пространство, на котором множество всех состояний системы представлено так, что каждому возможному состоянию системы соответствует одна и только одна точка этого пространства (изображающая точка) и, наоборот, каждой точке этого пространства соответствует одно и только одно состояние системы. Таким образом, изменению состояний системы, – т.е. её динамике – можно соподчинить движение изображающей точки; траекторию этой точки называют фазовой траекторией (её не следует смешивать с действительной траекторией движения), а скорость такой изображающей точки – фазовой скоростью. Как правило, выбирают пространства с евклидовой метрикой, используя либо декартову, либо полярную систему координат. Для систем с одной степенью свободы фазовое пространство вырождается в фазовую плоскость.

Фазовая траектория – траектория перемещения точки, отображающей состояние динамической системы, в фазовом пространстве; совокупность точек на фазовой плоскости, положение которых соответствует состояниям системы в процессе изменения во времени переменных x(t) и y(t), согласно заданным уравнениям исследуемой системы набор точек в фазовом пространстве, последовательно посещаемых системой. Траектория материальной точки – линия в пространстве, по которой движется тело, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения. Иногда фазовую траекторию называют орбитой.

http://profbeckman.narod.ru/

Фазовая плоскость – координатная плоскость, в которой по осям координат откладываются какие-либо две переменные (фазовые координаты), однозначно определяющие состояние системы второго порядка. Фазовая плоскость является частным случаем фазового пространства, которое может иметь большую размерность.

Фазовый портрет – топологическое представление зависимости друг от друга величин, описывающих состояние системы (динамических переменных) или фазового пространства; это совокупность фазовых траекторий при различных начальных значениях переменных.

Число степеней свободы динамической системы - размерность её фазового пространства, т. е. количество переменных, которые необходимы для полного описания системы. В контексте гамильтоновых систем число степеней свободы - число пар переменных состояния.

Динамические режимы, такие как состояние покоя или периодические колебания, соответствуют геометрическим объектам, таким как точка или замкнутая кривая, в фазовом пространстве. Эволюция динамической системы соответствует траектории (или орбите) в фазовом пространстве. Различные начальные состояния приводят к различным траекториям. Множество всех траекторий формирует фазовый портрет динамической системы, хотя на практике рассматриваются только репрезентативные траектории. Поскольку, как правило, невозможно получить явную формулу для решения нелинейного уравнения, анализ фазовых портретов является чрезвычайно полезным способом визуализации и понимания качественных характеристик решений.

Решения ОДУ часто удобнее изображать не в привычном виде u1(t),...,uN(t), которые называются растровыми графиками, а в фазовом пространстве, по осям которого откладываются значения каждой из найденных функций. Такой график - фазовый портрет системы – является кривой в фазовом пространстве и поэтому особенно нагляден. Размерность фазового пространства равна числу неизвестных N, а аргумент t входит в графики лишь параметрически.

В случае механического движения фазовый портрет график типа координата – скорость, в электричестве – заряд-ток, в популяционной задаче – количество хищников – жертв и т.д. На фазовом портрете размерность высоты представляет длину векторов. Важно, что фазовый портрет можно построить, не решая динамические уравнения системы. Фазовый портрет облегчает анализ поведения динамической системы. Он вычисляется путём взятия интеграла уравнений, порождающих пространство состояний. Построение паттерна помогает сделать выводы о характеристике изменений переменных x и y без знания аналитических решений исходной систем уравнений.

Точечная система – система, которая описываются обыкновенным дифференциальным уравнением.

Изображающая точка – точка на фазовой плоскости, за поведением которой ведётся наблюдение.

Особенность фазового пространства заключается в том, что состояние сколь угодно сложной системы представляется в нём одной единственной точкой, а эволюция этой системы – перемещением этой точки. При рассмотрении нескольких одинаковых систем, задаётся несколько точек в фазовом пространстве. Совокупность таких систем называют статистическим ансамблем. В классической механике фазовыми пространствами служат гладкие многообразия.

Фазовое пространство – это график, показывающий все возможные состояния системы. В фазовом пространстве значение переменной наносится против возможных величин других переменных в один и тот же момент времени. Если система описывается тремя переменными, строится трёхмерное фазовое пространство, в котором каждой переменной соответствует одна размерность.

В фазовом пространстве каждая степень свободы или параметр системы представляется в виде оси многомерного пространства; одномерная система называется

http://profbeckman.narod.ru/

фазовой траекторией, а двумерная система – фазовой плоскостью. Для каждого возможного состояния системы или допускаемой комбинации значений параметров системы точка включается в многомерное пространство. Траектория фазового пространства представляет собой набор состояний, совместимых с началом от одного конкретного начального условия, расположенного в полном фазовом пространстве, которое представляет собой набор состояний, совместимых с любым начальным условием. В целом фазовая диаграмма отражает все изменения состояний в системе, и ее форма позволяет легко выявить качества системы, которые другим способом не обнаруживаются. Фазовое пространство может содержать большое количество измерений. Например, газ с большим числом молекул, может потребовать отдельного измерения для каждой частицы x, y и z положений и импульсов, а также любого количества других свойств.

Если состояние динамической системы может быть задано скалярным значением (x R1), то система является одномерной. Часто только подмножество фазовой линии R1 соответствует физически значимым состояниям системы, и часто более естественно рассматривать одномерные фазовые пространства в виде интервалов и окружностей. Например, система может представлять собой химическую реакцию, характеризующуюся концентрацией реагента или RC-контур, характеризуемый напряжением на конденсаторе. В первом случае используют только неотрицательные значения R1, поэтому фазовое пространство [0, ].

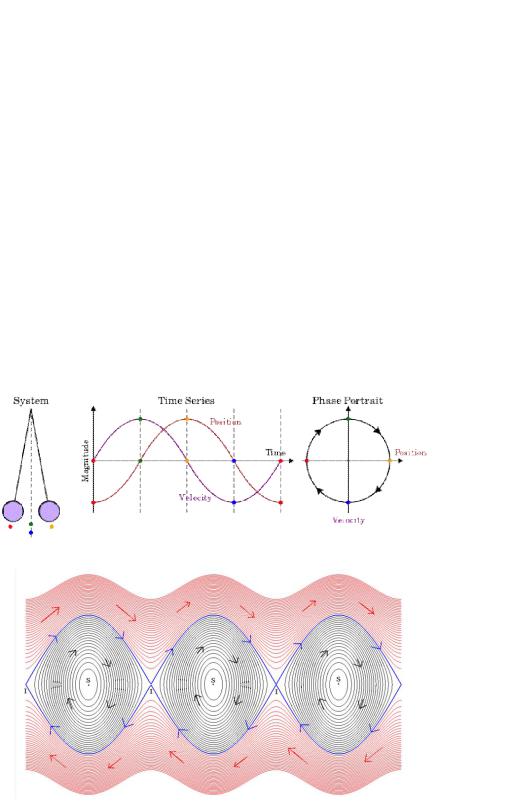
Рис. 5. Схема построения фазового портрета движения простого маятника.

Рис. 6. Зависимость потока от времени, рассчитанная по уравнению колебания маятника и представленная в фазовом пространстве. На оси x – положение маятника,

а на оси y – его скорость.

Фазовое пространство двумерной системы называется фазовой плоскостью, которая встречается в классической механике для одной частицы, движущейся в одном измерении, и где две переменные – это положение частицы и её скорость. В этом случае эскиз фазового портрета может дать качественную информацию о динамике системы. Примером является осциллятор Ван дер Поля.

http://profbeckman.narod.ru/

Рис. 5. иллюстрирует схему построения фазового портрета на примере на примере простого маятника; на рис. 6 представлен его фазовый портрет.

У простых систем в фазовом пространстве может быть не более одного или двух степеней свободы. Одна степень свободы есть у автономного ОДУ с одной переменной, одномерной системы можно судить по форме фазовой траектории. Простейшими примерами являются экспоненциальная модель роста/распад (одно неустойчивое/устойчивое равновесие) и модель логистического роста (два равновесия, одно стабильное, одно неустойчивое).

При помощи уравнений траектории в фазовом пространстве (фазовой плоскости) для исследуемой системы строят интегральные кривые, – т.е. кривые в фазовом пространстве такие, что в каждой их точке касательная имеет наклон, задаваемый уравнением траектории. Геометрическое построение интегральных кривых называют «качественным интегрированием уравнений». Понятия «интегральная кривая» и «фазовая траектория» в общем случае следует различать, так как одна интегральная кривая может состоять не из одной, а сразу из нескольких фазовых траекторий. Картину кривых в фазовом пространстве (на фазовой плоскости) можно описать либо одним уравнением – в координатной форме, т.е. при помощи уравнений, которые не содержат времени, – и изучать с его помощью интегральные кривые, либо описать системой уравнений в параметрической форме, – где независимая переменная (время t) выполняет роль параметра – и изучать фазовые траектории. Необходимость различения этих двух способов изображения одного и того же семейства кривых можно продемонстрировать на примере простейшей консервативной системы, описываемой уравнением x f (x) в этом случае для особой точки условия теоремы Коши окажутся нарушенными при рассмотрении координатного уравнения, но будут выполнены для уравнения, записанного в параметрической форме. Целой фазовой траекторией называют ту кривую в фазовом пространстве, которую описывает изображающая точка за всё время своего движения (от t=- до t=+ ).

Фазовый портрет исследуемой системы – это совокупность фазовых траекторий для всевозможных начальных условий. Его можно рассматривать как интегральное многообразие. Поскольку при изучении поведения системы интересуются, прежде всего, стационарными движениями в системе, то фазовый портрет можно также рассматривать как разбиение фазового пространства на области притяжения стационарных решений.

На основании особенностей фазового портрета характера можно провести классификацию особых точек системы уравнений (см. далее). Важно, что при изменении параметров системы, фазовая плоскость обычно как-то деформируется. Качественному изменению фазовой плоскости соответствует исчезновение существующих и рождение новых стационарных решений, – и такое изменение фазовой плоскости называют бифуркационной ситуацией.

Для удобства, изучение фазового портрета системы разделяют на исследование характера движений системы вблизи состояний равновесия, и на всей фазовой плоскости. При изучении фазового портрета интересует, прежде всего, общая топологическая картина движений на фазовой плоскости. Фазовая скорость – это скорость изменения состояния системы; она соответствует скорости движения изображающей точки в фазовом пространстве. Для вычисления величины фазовой скорости вводят понятие «фазовый радиус-вектор», как это делается в классической механике. Вычисление фазовой скоростью даёт возможность более точно прослеживать изменения в системе. Так, к примеру, в случае бифуркации седло-узел можно обнаружить область состояний системы, в которой происходит значительное уменьшение модуля фазовой скорости.

Основные свойства траекторий в фазовом пространстве:

1. В любой заданный момент времени траектории в фазовом пространстве не пересекаются.

http://profbeckman.narod.ru/

2. Любая граница C1, охватывающая в момент времени t1 в фазовом пространстве некое множество начальных условий к моменту t2 трансформируется в границу C2 охватывающее то же множество траекторий. Поэтому для понимания временной эволюции подмножества достаточно знать поведение его границы.

Фазовый портрет представляет собой геометрическое представление структуры фазовых траекторий динамической системы и потому полезный инструмент анализа её качественных свойств. Однако фазовая диаграмма может использоваться только для исследования динамических систем одного, двух и (иногда) трёх измерений.

где x dx – производная от переменной состояния x по времени t. Это ОДУ является dt

автономным, т. к. f явно не зависит от времени t.

Фазовая траектория одномерного ОДУ разделена точками равновесия (точки, где f(x)=0) и отрезками, соединяющими точки равновесия. Устойчивость равновесия определяется направлениями траекторий, зависящими от знака правой части функции f(x). Для прогнозирования динамики системы и ее зависимости от начального условия нет необходимости решать Ур. 16 или знать особенности функции f(x).

Одномерные системы также могут быть заданы итерационным отображением в виде xt+1=f(xt), где состояние в момент времени t+1 является функцией состояния в момент времени t. Фазовые портреты таких систем могут быть довольно сложными, особенно когда динамика хаотична.

Одномерные пространства состояний могут быть очень сложными, например, графы или дендриты.

Если состояние конкретной динамической системы полностью характеризуется заданием п переменных, т. е. поведение системы описывается п обыкновенными дифференциальными уравнениями 1-го порядка

Тогда такой системе ставится в соответствие n-мерное фазовое пространство, по осям координат которой откладывают значения переменных х1, х2,..., хп (фазовых переменных). Определение нормы в этом пространстве вводится, исходя из смысла

соответствие, сопоставляющее каждой точке х Μ приложенный к ней вектор F пространства Rm.

Эволюция динамической системы определяется посредством задания значений фазовых переменных в начальный момент времени

и задания эволюционного оператора Тt, преобразующего начальное состояние в состояние в момент времени t (задача Коши): x(t)=Ttx(0) или Tt: xi(0) xi(t), i=1, 2,...,n.

Тем самым в фазовом пространстве выделяется фазовая траектория, проходящая через точку х(0). Оператор Тt задаёт однопараметрическую группу преобразований фазового пространства на себя (параметр - время t) и удовлетворяет групповому свойству ТtТт=Тt+т. Группа преобразований фазового пространства, задаваемая оператором Tt называется фазовым потоком.

Если начальные точки не лежат на одной фазовой траектории, т. е. не могут быть получены одна из другой сдвигом с помощью оператора Тt за какое-либо конечное время t, то они порождают различные фазовые траектории. Совокупность всевозможных

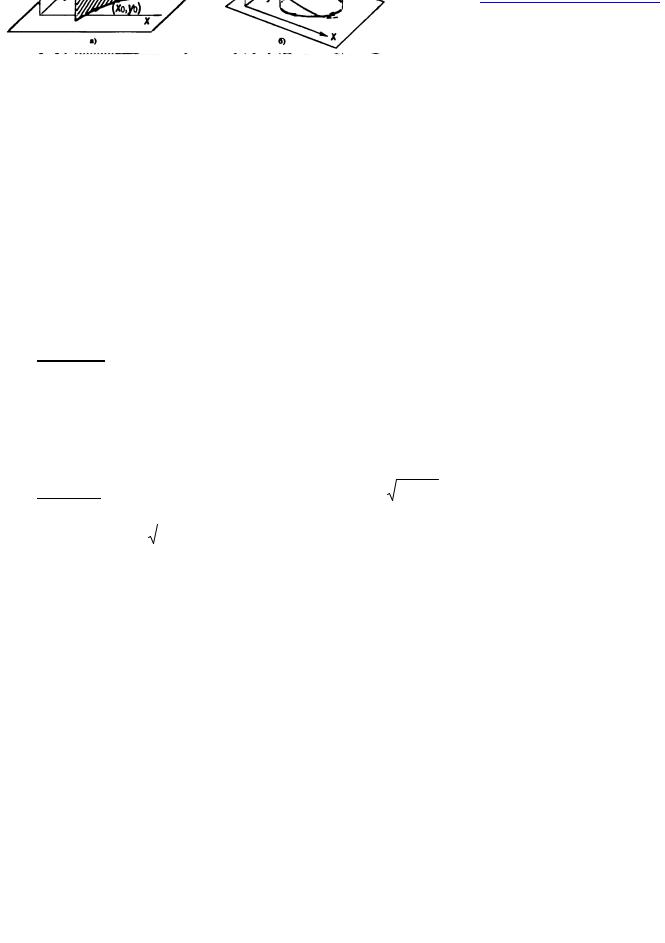
http://profbeckman.narod.ru/

фазовых траекторий образует фазовый портрет динамической системы. Изучение фазовых портретов как способа геометрических представления решений обыкновенных дифференциальных уравнений было начато А. Пуанкаре в конце 19 в.

Различные фазовые траектории одной достаточно гладкой динамической системы не пересекаются в фазовом пространстве (в противном случае, выбирая точку пересечения за начальное условие, мы получили бы, что из одной точки начинаются более одной фазовой траектории; последнее противоречит теореме Коши). Фазовые траектории могут представлять собой либо отдельные точки, либо замкнутые кривые, либо отрезки кривых конечной длины, заключённые между двумя точками (последние не принадлежат данной траектории), либо кривые, неограниченные в одну или обе стороны. Траектории, являющиеся точками, называются особыми точками и отвечают стационарным состояниям динамической системы. Классификация структурных элементов фазового портрета выполнена в теории колебаний.

Во многих случаях необходимо рассматривать зависимость свойств системы от каких- -либо параметров, например, изучать систему, описываемую уравнением

параметрами являются и .

Все системы (19) (т. е. отвечающие различным значениям ) можно рассматривать с помощью одного и того же фазового пространства. Это позволяет сопоставлять свойства систем, отличающихся конкретными значениями параметров. Например, может оказаться, что в некоторых интервалах значений для траекторий доступны не все области фазового пространства из числа тех, которые доступны при других значениях.

доступно всё фазовое пространство (при подходящем выборе начальных условий), тогда как при

Семейством ОДУ называется множество систем уравнении вида

заданных в фазовом пространстве М векторными полями F, зависящими от координат векторов системных параметров μ, лежащих в области L пространства Rk.

Потенциалом в теории динамических систем называется величина

x

U x, F z, dz

где точка над буквой означает дифференцирование по t. Область Μ называется фазовым пространством системы, а прямое произведение IхΜ – расширенным фазовым пространством, где I – интервал вещественной оси времени t.

Рис. 7. Проекции отрезка интегральной кривой или спирали с шагом на фазовую плоскость (х,у) в виде отрезка (а) и замкнутой

кривой (б).