
- •Аннотация
- •От автора
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •1. СИСТЕМЫ И ПРОЦЕССЫ
- •2. ПОРЯДОК, НЕПОРЯДОК, БЕСПОРЯДОК И ХАОС
- •3. ТЕРМОДИНАМИКА
- •3.1 Начала термодинамики
- •3.2 Равновесная термодинамика
- •4. НЕРАВНОВЕСНАЯ ТЕРМОДИНАМИКА
- •4.1 Диссипативные структуры, системы и среды
- •4.2 Термодинамика необратимых процессов
- •4.3 Линейная неравновесная термодинамика
- •4.4 Нелинейная неравновесная термодинамика
- •4.5 Статистическая термодинамика
- •5. ЭНТРОПИЯ
- •5.1 Определение и свойства энтропии
- •5.2 Энтропия в химической термодинамике
- •5.3 Энтропия в статистической физике
- •5.3.1 Энтропия Больцмана-Планка
- •5.3.2 Энтропия Гиббса
- •5.4 Тсаллис (Цаллис) энтропия (Революция в термодинамике)
- •6. ГЕОМЕТРИЯ ФРАКТАЛОВ
- •6.1 Элементы геометрии фракталов
- •6.2 Размерности фракталов
- •6.3 Примеры фракталов
- •6.4 Фракталы и энтропия
- •7. ИНФОРМАТИКА
- •7.1 Информация, информатика и информационные технологии
- •7.2 Теория информации
- •7.2.1 Информация Хартли
- •7.2.2 Энтропия Шеннона
- •7.3 Отрицательная энтропия, антиэнтропия, экстропия
- •7.4 Алгоритмическая теория информации
- •7.4.1 Энтропия Колмогорова
- •7.4.2 Эпсилон-энтропия
- •7.5 Энтропия Кульбака-Лернера
- •7.6 Энтропия Реньи
- •7.7 Квантовая информатика
- •7.7.1 Некоторые положения квантовой механики
- •7.7.2 Энтропия фон Неймана
- •7.7.3 Линейная энтропия
- •7.7.4 Сравнение энтропий Реньи, Цаллиса и Неймана
- •7.7.5 Энтропия Холево
- •8. СИНЕРГЕТИКА
- •8.1 Синергизм и синергетика
- •8.2 Детерминизм, случайность и неопределённость
- •8.3 Простые и сложные системы
- •8.4 Анализ систем
- •8.5 Параметры порядка (управляющие параметры)
- •8.6 Процессы самоорганизации
- •9. СИСТЕМЫ И ЗАКОНЫ ИХ ЭВОЛЮЦИИ
- •9.1 Статические системы
- •9.2 Динамические системы
- •9.3 Линейные динамические системы
- •9.4 Нелинейные динамические системы
- •9.5 Эволюция динамической системы
- •9.6 Математическое описание эволюции динамической системы
- •10. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ОПИСАНИИ ДИНАМИЧЕСКИХ СИСТЕМ
- •10.1 Обыкновенные дифференциальные уравнения
- •10.2 Фазовое пространство и пространство состояний
- •10.3 Линейные ОДУ на плоскости
- •10.4 Нелинейные дифференциальные уравнения
- •11. ОТОБРАЖЕНИЯ
- •11.1 Системы с дискретным временем в отображениях
- •11.2 Итерации в исследовании динамических систем
- •11.3 Графические методы нахождения неподвижных точек и исследования их свойств
- •11.4 Многопараметрические отображения
- •11.5 Примеры некоторых важные отображений
- •12. ОСОБЫЕ ТОЧКИ ФАЗОВЫХ ПОРТРЕТОВ ДИНАМИЧЕСКИХ СИСТЕМ
- •12.1 Дифференциальные уравнения и особые точки
- •12.2 Классификация точек равновесия
- •12.3 Фазовые портреты и особые точки нелинейных ОДУ
- •12.4 Многомерные системы
- •13. РЕГУЛЯРНЫЕ АТТРАКТОРЫ И РЕПЕЛЛЕРЫ
- •13.1 Типы аттракторов
- •13.2 Фазовый объём
- •13.3 Репеллеры
- •13.4 Осциллятор и осцилляции
- •14. УСТОЙЧИВОСТЬ ДИНАМИЧЕСКИХ СИСТЕМ
- •14.1 Устойчивые и неустойчивые равновесия
- •14.2 Устойчивость по Ляпунову (метод первого приближения)
- •14.3 Показатель Ляпунова
- •14.4 Устойчивость нелинейной системы
- •14.5 Метод функций Ляпунова
- •14.6 Функция Ляпунова и энтропия
- •14.7 Асимптотическая устойчивость
- •14.8 Устойчивость особых точек
- •14.9 Устойчивость особых точек
- •14.10 Устойчивость решений дискретных уравнений
- •15. БИФУРКАЦИИ
- •15.1 Бифуркации: основные понятия и классификация
- •15.2 Элементы теории бифуркаций
- •15.3 Простейшие бифуркации
- •16. БИФУРКАЦИИ ЦИКЛОВ
- •16.1 Предельные циклы
- •16.2 Устойчивость предельных циклов
- •16.3 Бифуркации устойчивых предельных циклов
- •16.5 Бифуркация рождения пары устойчивых замкнутых траекторий.
- •16.6 Транскритическая (обмена устойчивостью между циклами) бифуркация.
- •16.7 Бифуркация исчезновения (рождения) пары замкнутых траекторий.
- •16.8 Бифуркация удвоения периода цикла
- •16.9 Бифуркация рождения (гибели) двумерного тора.
- •16.10 Гомоклиническая бифуркация рождения/исчезновения цикла
- •17. ДИНАМИЧЕСКИЙ ХАОС
- •17.1 Хаос статистический и динамический
- •17.2 Предсказание статического поведения системы
- •17.3 Сценарии перехода к хаосу
- •17.4 Примеры систем с хаосом
- •18. ХАОС В ЛИНЕЙНЫХ ОДНОМЕРНЫХ СИСТЕМАХ
- •18.1 Бифуркационные диаграммы
- •18.2 Лестница Ламерея
- •18.3 Отображение Бернулли
- •18.4 Треугольное отображение
- •18.5 Отображение «тент»
- •18.6 Канторов репеллер
- •18.7 Детерминированная диффузия
- •19. ХАОС В ЛОГИСТИЧЕСКОМ ОТОБРАЖЕНИИ
- •19.1 Переход к хаосу через удвоение периода
- •19.2 Логистическое уравнение
- •19.3 Дискретное логистическое уравнение
- •19.4 Логистическое отображение
- •19.5 Бифуркационная диаграмма логистического отображения
- •19.6 Цикл периода 3
- •19.7 Фазовые диаграммы логистического отображения
- •19.8 Аттракторы и фракталы в логистическом отображении
- •20. ХАОС В НЕЛИНЕЙНЫХ ОДНОМЕРНЫХ ОТОБРАЖЕНИЯХ
- •20.1 Отображение xn+1=С+xn2.
- •20.2 Отображение xn+1=а-xn2.
- •20.3 Подобие окон периодической динамики
- •20.4 Порядок Шарковского
- •20.5 Универсальность Фейгенбаума
- •20.6 Устойчивость циклов одномерных отображений
- •20.7 Топологическая энтропия
- •20.8 Синус-отображение
- •21. ХАОС В НЕЛИНЕЙНЫХ ДВУМЕРНЫХ ОТОБРАЖЕНИЯХ
- •21.1 Отображение Эно (Henon map)
- •21.2 Отображение подковы и отображение пекаря
- •21.3 Отображение «кот Арнольда» (Arnold’s cat map)
- •22. НЕРЕГУЛЯРНЫЕ АТТРАКТОРЫ
- •22.1 Хаос в консервативных и диссипативных системах
- •22.2 Регулярные и хаотические аттракторы
- •22.3 Квазиаттракторы
- •22.4 Хаотически аттракторы
- •22.5 Негиперболические хаотические аттракторы
- •22.6 Фрактальные аттракторы
- •22.7 Характеристика нерегулярных аттракторов
- •22.8 Странные нехаотические аттракторы
- •22.9 Сингулярные аттракторы
- •22.10 Многомерные нерегулярные аттракторы
- •22.11 Дикие аттракторы

http://profbeckman.narod.ru/
возрастая, проходит значение 3/2, в системе возникает устойчивый цикл. Этому циклу в системе Ланфорда соответствует инвариантный тор.
Как следует из теоремы Пуанкаре-Бендиксона, в двумерном случае (на плоскости) автономная система нелинейных дифференциальных уравнений может иметь только простейшие регулярные аттракторы – устойчивые особые точки и простые предельные циклы. Следовательно, сложные регулярные аттракторы (торы и сложные предельные циклы удвоенного и более периодов) и сингулярные аттракторы автономная система нелинейных дифференциальных уравнений может иметь только в случае размерности фазового пространства n>3. Трёхмерные автономные системы уже могут иметь устойчивые предельные циклы любого периода, циклические сингулярные аттракторы любой сложности и простые устойчивые двумерные торы. А четырёхмерные автономные системы уже могут иметь устойчивые двумерные торы любого периода, тороидальные сингулярные двумерные аттракторы любой сложности и простые устойчивые трёхмерные торы и т.д.
13.2Фазовый объём
Ксожалению, в настоящее время невозможно точно предсказать существование аттрактора в динамической системе. Есть только некоторые примерные критерии. Один из них – наличие полупроницаемых поверхностей – замкнутых поверхностей, на которых векторное поле направлено внутрь ограничиваемой области. Тогда траектории с поверхности входят в область и уже не покидают ее. В указанной ситуации область, скорее всего, содержит аттрактор
Другой критерий – динамика объёма областей в фазовом пространстве. Сокращение фазового объёма указывает на возможность аттрактора. Например, этот критерий показывает, что в отличие от консервативной (гамильтоновой) диссипативная система имеет аттрактор.
Эволюцию динамической системы удобно описывать через изменение во времени фазового объёма конечной фазовой области.
Фазовый объём – объём в фазовом пространстве.
Для механической системы с N степенями свободы элементарный фазовый объём равен: dpdq=dpldq1...dpNdqN, где q1,...,qN – обобщённые координаты, a p1,...,рN – обобщённые импульсы системы. Фазовый объём конечной фазовой области G равен 2N-
мерному интегралу dpdq . Если система описывается уравнениями Гамильтона, то при
G
движении частиц фазовый объём остаётся неизменным (теорема Лиувилля). Это позволяет ввести нормированные функции распределения в фазовом пространстве. В негамильтоновой системе фазовый объём может, как увеличиваться, так и уменьшаться.
Теорема Лиувиллия: Пусть f(p, q, t) – плотность вероятности ансамбля траекторий, тогда использование уравнения Гамильтона даёт df/dt=0. Плотность вероятности вдоль траектории сохраняется (несжимаемость потока).
Теорема Лиувилля о сохранении фазового объёма – функция распределения гамильтоновой системы постоянна вдоль любой траектории в фазовом пространстве. Теорема утверждает сохранение во времени фазового объёма, или плотности вероятности в фазовом пространстве.
Система х F(x) называется консервативной, если объём произвольной области
фазового пространства не меняется со временем, и диссипативной, если объём некоторой области фазового пространства со временем уменьшается. Если всюду в фазовом пространстве divF(х)=0, то система сохраняет объем и является консервативной. Если же существует область фазового пространства, в которой divF(х)<0, то система х F(x) – диссипативна в этой области.
Примером систем, сохраняющих фазовый объём, являются гамилътоновы системы

http://profbeckman.narod.ru/
В консер ватив ной системе элемент в фазовом пространстве только изменяет форму, но сохраняет объём (выполняется теорема Лиувилля), что предопределяет характер эволюции и тип хаотичности, возникающий в консервативных системах. Консервативные системы характеризуются неизменным во времени запасом энергии. В механике их называют гамильтоновыми. Механические колебательные системы в отсутствие трения относятся к консервативным системам. В консервативных системах хаотические орбиты стремятся однородно заполнить все части некоторого подпространства в фазовом пространстве, т.е. они характеризуются однородной
плотностью вероятности в ограниченных областях фазового пространства.
Рис. 15. Сохранение фазового объёма при эволюции гамильтоновой системы.
Для систем с двумя степенями свободы фазовое пространство четырёхмерно. Примером является система двух гармонических осцилляторов единичной массы. В
случае полностью интегрируемых систем с n степенями свободы фазовое пространство 2n-мерно и в переменных действие-угол имеет структуру множества n-мерных торов. Любая возможная траектория располагается на одном из них. При этом некоторые траектории могут оказаться замкнутыми, другие же будут всюду плотно покрывать поверхность соответствующего тора. В диссипатив ной систем е из-за диссипации энергии объём элемента фазового пространства сокращается с течением времени (теорема Луивилля не соблюдается). Поэтому в фазовом пространстве диссипативных систем появляются притягивающие множества, которые не существуют в консервативных системах – аттракторы.
Для систем, сохраняющих фазовый объём, не могут существовать в фазовом пространстве такие структурные элементы, как аттракторы и репеллоры, поскольку наличие первых означало бы уменьшение, а вторых – увеличение фазового объёма. В таких системах нет структурных элементов, обладающих свойством асимптотической устойчивости при t (либо аналогичным свойством при t ).
Рис. 16. Деформация "фазовой капли" в случае устойчивого (а) и неустойчивого (б) движения 1 гамильтоновой системы (объём капли сохраняется).
В условиях сохранения фазового объёма форма фазовой капли может меняться как незначительно (устойчивое движение), так и сильно (неустойчивое движение). Наличие неустойчивости может приводить к сложному (стохастическому) поведению системы.
Если физическая система составлена из большого числа частиц, то целесообразно использовать статистические методы описания. При уменьшении фазового объёма V траектории могут стремиться к некоторой поверхности в исходном фазовом пространстве, имеющей размерность D=n-k, где k-целое, k n. В частном случае k=n это отвечает приближению к некоторому стационарному состоянию – особой точке в фазовом пространстве. Однако при V 0 может существовать предельное множество (аттрактор), мера которого имеет размерность d>1 (дробную фрактальную размерность). Такая ситуация реализуется, когда фазовое пространство содержит странный аттрактор.
Для систем с любой размерности, удовлетворяющих уравнениям Гамильтона, площадь фазового пространства, пронизываемого траекториями частиц, от времени не зависит. Однако это не соблюдается при наличии негамильтоновой силы, т. е. силы, не

http://profbeckman.narod.ru/
имеющие потенциальной функции. Статистическими методами можно показать, для негамильтоновых систем плотность и соответственно объем фазового пространства в окрестности частицы в общем случае не являются сохраняющимися величинами. Так, действие излучения уменьшает фазовый объём, а процессы столкновения его увеличивают. Однако, плотность и объём в фазовом пространстве могут сохраняться для систем с негамильтоновыми силами при условии, что они не зависят от импульса.
Рис. |
17. |
К |
определению |
консервативных (а) и диссипативных (б) динамических систем.
Системы с конечномерным фазового пространства являются идеализированным образом реальных физических систем. Например, при описании теплового, электромагнитного и других полей, различного рода взаимодействий и т. д. приходится иметь дело с характеристиками, заданными в пространстве: температурой Т(r,t), напряжённостью поля E(r,t) и др. Для этих характеристик также задаются некоторые эволюционные уравнения. Теперь, однако, фазовое пространство такой динамической системы является уже бесконечномерным.
Иногда путём подходящего выбора базиса удаётся свести фазовое пространство к счётномерному. Наконец, в ряде случаев с достаточной точностью можно описать поведение распределённой системы с помощью некоторого конечного числа функций времени. Тем самым исходное (бесконечномерное) фазовое пространство редуцируется к фазовому пространству конечной размерности. Это отвечает выделению существенных переменных ("параметров порядка") и пренебрежению всеми прочими ("подчинёнными") переменными. По существу сходная процедура реализуется при численном интегрировании уравнений в частных производных.
Фазовая траектория гармонических колебаний (например, собственных колебаний линейного осциллятора в отсутствие трения) представляет собой эллипс (или окружность при соответствующем выборе масштаба). Точки, где фазовая траектория пересекает ось абсцисс (в этих точках поворота скорость изменяет знак), соответствуют максимальным отклонениям ротора из положения равновесия.
Для диссипативных систем характерно, что с течением времени облако изображающих точек "съёживается" и концентрируется на одном или нескольких аттракторах – подмножествах фазового пространства, обладающих обычно нулевым фазовым объёмом (рис. 12б). С точки зрения динамики во времени это означает, что режим, возникающий в системе, предоставленной себе в течение длительного времени, становится независящим от начального состояния.
13.3 Репеллеры
Понятию «аттрактор» противостоит понятие «репеллер» – набор параметров и их значений, которые «отталкивают» систему от положения равновесия в том смысле, что он вводит ограничения различной природы на свободу стремления системы к цели, к равновесию. Если аттрактор обозначает то состояние равновесия системы, к которому она стремится как к своей цели, то репеллер выражает своим содержанием все ограничения и запреты для системы. Большинство реально существующих сложных систем нечётко определены, и их параметры находятся в сложных, противоречивых взаимосвязях. По этой причине в сложных системах часто наблюдаются острые противоречия между

http://profbeckman.narod.ru/
требованиями к поведению системы со стороны аттракторов и со стороны репеллеров. Противоречивые требования к сложной системе со стороны аттракторов и репеллеров не приводят к её распаду благодаря тому, что она иерархична. Разные составляющие иерархии в процессе самоорганизации приобретают противоположные качества. Одни удовлетворяют требованиям аттракторов, другие – репеллеров. В целом, динамическая система, сохраняя свою структуру и цели, приобретает полярно противоположные свойства и возможность альтернативного
поведения.
Рис. 18. Аттрактор репеллер – неустойчивое состояние, при котором система или переменная удаляется во времени.
Репеллер – область фазового пространства, отклоняющая фазовые траектории движения системы; математический образ какого-либо объекта, представляемого в виде отталкивающего множества в фазовом пространстве управляемого объекта или системы.
Репеллер (отталкиватель) – аттрактор, к которому стремится фазовая траектория при t -. Это неустойчивое состояние, которое система или переменная удаляется во времени от исходного состояния. Реппелентность: степень, в которой система удаляется от исходного состояния. В теории динамических систем рассматривается как противоположность аттрактора (притяжение): аттрактор устойчив к возмущениям, а репеллер - нет.
Репельность – активность, с которой система удаляется от исходного состояния.
Как и аттракторы, репеллеры могут быть как регулярными, так и странными. Примерами странных репеллеров являются отображение пекаря и подкова Смейла, которые имеют сложную хаотическую динамику.
Если аттрактор – математический образ установившихся режимов, представляемый в виде притягивающего множества в фазовом пространстве объекта или системы, то репеллер – математический образ какого-либо объекта, представляемого в виде отталкивающего множества в фазовом пространстве управляемого объекта или системы. Аттрактор – асимптотически устойчивое решение замкнутой системы, а репеллер – область фазового пространства, отклоняющая фазовые траектории движения системы. Часто в сложной системе аттракторы и репеллеры пересекаются и даже образуют единое целое. Репеллер с фиксированной точкой: состояние, в котором система удаляется от исходного значения. Система нестабильна в местоположении репеллера с фиксированной точкой. На практике встречается редко. Пример: вертикально стоящий карандаш. Графически репеллеры с фиксированной точкой идентичны аттракторам с
фиксированной точкой, но имеют другую направленность.
Рис. 19. Стабильные и нестабильные состояния.
Репеллер – область фазового пространства, отклоняющая фазовые траектории движения системы; математический образ какого-либо объекта, представляемого в виде отталкивающего множества в фазовом пространстве управляемого объекта или системы.
Возмущение: небольшие изменения в системе из-за частей системы, которые необходимы, но не моделируются. Они отличаются устойчивостью заданной
точки тем, что аттрактор устойчив к возмущениям, а репеллер – нет. Это видно на рис. 19. Небольшое возмущение могло бы нарушить шар 1, но оно опустится обратно в нижнюю часть аттрактора, в котором он находится сейчас. Шар 2, напротив, был бы смещен вдали от своего текущего положения даже незначительным возмущением, поскольку часть системы, где она показана, является репеллером. Для шара 3

http://profbeckman.narod.ru/
требуется большое возмущение, чтобы вытащить его из бассейна сильного аттрактора, где он находится в настоящее время.
Рис. 20. Графическое изображение состояний аттракторов и репеллеров, описываемых динамической теорией систем.
Из стабильного состояния система вряд ли выйдет. Состояния 1 и 3 на рис. 19 являются стабильными (3 более устойчиво, т. е. является более сильным аттрактором), а 2 неустойчиво. Такая система (имеющая несколько устойчивых состояний) является многостабильной. Возмущение способно вывести систему из равновесного состояния. При этом аттрактор устойчив к возмущениям, а репеллер нет. Так, сравнительно небольшое возмущение способно сместить шар 1, при этом он переместится в нижнюю часть аттрактора, напротив, шар 2 будет смещён со своего места пребывания самым небольшим воздействием, поскольку он находится в репеллере; для шара 3 требуется очень сильное воздействие, чтобы извлечь его из потенциальной ямы.
Состояния репеллеров (рис. 20а) неустойчивы и изображаются как холмы, потому что шар отходит от своей заданной точки в верхней части холма в ответ на даже очень небольшое возмущение, тогда как аттракторные состояния (рис. 20б) устойчивы и изображаются долинами, потому что шар возвращается к своей заданной точке в нижней части долины даже при большом количестве возмущений. Нестабильные состояния аттракторов (рис. 20в) изображаются «ступенчатой» конфигурацией, которые характеризуются устойчивыми состояниями только в том случае, если шар испытывает минимальное возмущение, но становятся неустойчивыми в ответ на большие возмущения. В этом последнем сценарии шар переходит в новую (более низкое) состояние и гораздо реже возвращается к предыдущему (более высокому) заданному значению, чем движется к нижней точке заданного значения.
Репеллеры характеризуют систему в своём развитии активно удаляющуюся от исходной точки. Такая система чрезвычайно нестабильна. Примером служит карандаш, вертикально установленный на грифеле: достаточно его отпустить, чтобы он немедленно свалился. Скорость приближения или удаления от заданного состояния определяется величиной показателя Ляпунова (см. далее).
Пейзаж аттрактора для закрепленных на чаше отдельных элементов внутри системы будет стремиться сходиться к бассейну чаши. В самой нижней части чаши отмечается местоположение аттрактора с фиксированной точкой. Пейзаж аттрактора для фиксированной точки репеллера подобен холму или горному пику имеет тенденцию быстро покидать пик репеллера.
Рис. 21. Аттрактора ландшафт для седла (на котором находится шар) показывающий седло между двумя аттракторными бассейнами. Любой элемент на седле будет высоко нестабилен и будет стремиться свалиться в один из двух аттракторных бассейнов.
Спиральный аттрактор – топологическая особенность, объединяющая неподвижный точечный аттрактор с предельным циклом; состояние системы движется по спирали к заданной точке.
Спиральный репеллер – топологическая особенность, объединяющая неподвижный точечный аттрактор с предельным циклом, состояние системы удаляется по спирали от заданной точки.
Рис. 22. Аттрактор (слева) и репеллер (справа).
Спиральный аттрактор (как и репеллер) обладает топологической особенностью, объединяющей неподвижный точечный аттрактор с предельным
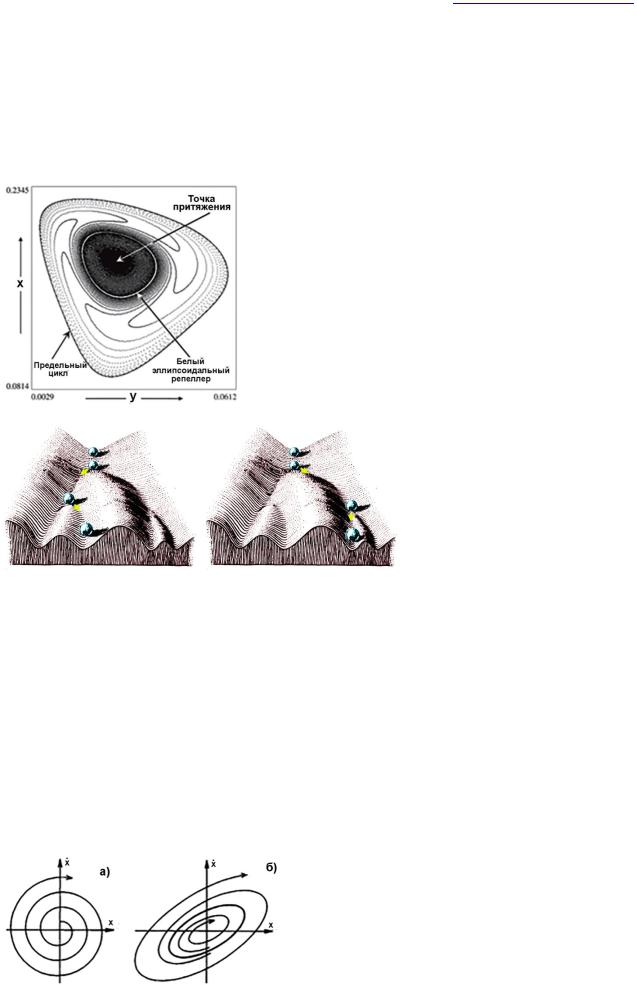
http://profbeckman.narod.ru/
циклом (график имеет вид спирали вокруг исходной точки).
Аттракторы и репеллеры появляются в предельных циклах. Подобно неподвижным точкам, предельные циклы являются или аттракторами или репеллерами.
Для систем с одной степенью свободы (их фазовое пространство – плоскость) устойчивыми предельными циклами и устойчивыми состояниями равновесия исчерпываются все возможные объекты, которые притягивают соседние траектории на фазовой плоскости. В многомерных динамических системах с размерностью фазового пространства n 3 возможны более сложные притягивающие объекты – аттракторы.
Рис. 23. Предельный цикл, аттрактор и репеллер.
Всякая достаточно близкая к предельному циклу траектория стремится к нему либо в прямом, либо в обратном времени. Типичная система с непрерывным временем на плоскости (состояние которой задаётся двумя вещественными параметрами, например, напряжением и током, или положением и скоростью точки на прямой) может стремиться только к положению равновесия или к предельному циклу.
В сложной системе обычно присутствуют и аттракторы и репеллеры. Примером может служить рельеф холмистой местности, по которому катятся шары (рис. 24).
Рис. 24. Пейзаж Ваддингтона
(1957). В этой версии фазового портрета возвышенности – репеллеры, а долины – аттракторы. Положение мяча представляет текущее состояние системы. Подобно тому, как рельеф поверхности ограничивает поток шаров, в динамической системе
аттракторы и репеллеры ограничивают динамику системы. Положение шара в зоне аттрактора устойчива, а в зоне репеллера – нет.
Если имеются несколько аттракторов в фазовом пространстве, то их область притяжения разделяется нестабильными множествами точек – репеллерами, так что все соседние фазовые траектории отталкиваются от этих множеств. Простейший репеллер: нестабильная сингулярная точка (рис. 25а); нестабильный предельный цикл (рис. 25б); нестабильный тор. И ещё репеллеры, как и аттракторы, могут быть сложно сформированными.
Аттракторы и репеллеры могут существовать только в диссипативных системах. Фазовый объём, занимаемый траекториями, формируемый аттракторами и репеллерами равен нулю. Следовательно, размерности аттракторов и репеллерами должны быть меньше размерности оригинального фазового пространства. Это важно для систем со многими степенями свободы и в частности непрерывных систем, поскольку последние имеют бесконечного размера фазовое пространство, но их размерность аттрактора имеет конечное значение. Факт, что размерность аттрактора непрерывной системы конечна
позволяет использовать, конечно, мерное фазовое пространство для исследования стационарных движений в такой системе.
Рис. 25 Простые репеллеры: (а) –
нестабильная сингулярная точка; (б) –
нестабильный предельный цикл.
Как правило, динамическая система
