http://profbeckman.narod.ru/

имеет много аттракторов и репеллеров. Динамика пары аттрактор-репеллер устроена достаточно просто: траектории, расположенные вне данных аттрактора и репеллера, начинаются вблизи репеллера и заканчиваются вблизи аттрактора. Если система имеет много аттракторов, то возникает сложная динамика между аттракторами и репеллерами. Для её описания используется такой объект как фильтрация – упорядоченная по включению последовательность аттракторов. Фильтрация помогает избавиться от аппаратного шума или малых флуктуаций, не связанных с поведением динамических систем. Шум влияет на притягивающее множество. Если аттрактор обладает канторовой структурой (например, аттрактор Фейгенбауэра), то при отсутствии шума, увеличение уровня разрешения, количество островов, в которых лежат точки изучаемого множества, будут непрерывно увеличиваться, тогда как в системе с шумом число этих островов будет расти до определённого предела.

13.4 Осциллятор и осцилляции

Примером динамической системы, описываемой решением нелинейного обыкновенного дифференциального уравнения, является колебания маятника с затуханием.

Идеальный маятник служит примером структурной неустойчивости: в отсутствие трения аттрактор не существует, но введение даже самого незначительного трения изменяет движение маятника и вводит аттрактор.

Сначала обсудим некоторые основные свойства осцилляторов, поскольку физика колебаний – важное направление использования аттракторов репеллеров и фазовых портретов.

Осцилляция – повторение состояния системы с течением времени. Маятник, качающийся назад и вперед, является классическим примером колебаний.

При анализе осцилляций на оси абсцисс фазовой плоскости откладывается значения параметра x, а на оси ординат – первая производная x по времени (скорость), что связывает ось ординат с импульсом. Каждая точка фазовой плоскости отражает одно состояние системы и называется фазовой, изображающей или представляющей точкой. Изменение состояния системы отображается на фазовой плоскости движением этой точки. След от движения изображающей точки называется фазовой траекторией. Через каждую точку фазовой плоскости проходит лишь одна фазовая траектория, за исключением особых точек. Стрелками на фазовых траекториях показывается перемещение изображающей точки с течением времени. Полная совокупность различных фазовых траекторий – это фазовый портрет. Он даёт представление о совокупности всех возможных состояний системы и типах возможных движений в ней. Фазовый портрет удобен для рассмотрения движений макроскопических и квантовых частиц.

Равновесие физической системы устойчиво, если при любом отклонении системы из положения равновесия возникает возрастающая или восстанавливающая сила, которая стремится вернуть систему в равновесие. Если систему вывести из устойчивого равновесия каким-либо внешним воздействием и затем предоставить самой себе, в системе будут происходить колебания около устойчивого положения равновесия. Такие колебания, происходящие в отсутствие периодического внешнего воздействия на систему, называют собственными колебаниями. Любая система, способная совершать

собственные колебания, называется осциллятором.

Рис. 26. Границы кольцевой области, образованные двумя концентрическими кругами. Все стрелки направления поля, пересекающие эти границы, указывают на кольцевую область.

http://profbeckman.narod.ru/

Если поле направления ориентировано внутрь вдоль границы кольцевой области, и если область не содержит неподвижных точек, то в кольцевой области присутствует предельный цикл – кольцевая область фазовой плоскости.

Если поле направления системы ориентировано внутрь вдоль границы кольцевой области, область называется областью захвата. Если в область захвата нет неподвижные точки, то она содержит предельный цикл.

В отсутствие трения энергия, сообщённая системе при начальном возбуждении, остаётся неизменной в процессе последующих собственных колебаний. Поэтому в идеализированных консервативных системах собственные колебания продолжаются неограниченно долго. В консервативных системах с одной степенью колебания продолжаются неограниченно долго. В консервативной системе с одной степенью свободы собственные колебания будут строго периодическими, так как начальное состояние системы воспроизводится через равные промежутки времени. При наличии трения, собственные колебания постепенно затухают из-за диссипации энергии и система приходит в состояние покоя в положении равновесия. Если восстанавливающая сила пропорциональна отклонению от положения равновесия, то такая система в отсутствие

трения, а также при наличии вязкого трения (когда сила трения пропорциональна скорости) описывается линейным дифференциальным уравнением. В отсутствие трения собственные колебания в линейной системе будут гармоническими (синусоидальными), а при слабом вязком трении – почти гармоническими (с экспоненциально убывающей амплитудой).

Рис. 27. Взаимное расположение фазовой плоскости и графиков потенциальной и полной энергии осциллятора на экране

Механическое состояние динамической системы в любой момент времени можно наглядно изобразить с помощью точки (изображающей точки) в фазовом пространстве. Для системы с одной степенью свободы, положение которой определяется единственной координатой, фазовое пространство динамических переменных двумерно, т. е. представляет собой плоскость. На такой фазовой плоскости по оси абсцисс отложена обобщенная

координата (угол отклонения) , а по оси ординат – угловая скорость . Очень наглядное графическое представление всему процессу эволюции механического состояния системы дает фазовая диаграмма, т. е. линия, которую изображающая точка вычерчивает на фазовой плоскости. Если система совершает периодическое движение, изображающая точка на фазовой плоскости описывает замкнутую кривую, двигаясь по ней в направлении по часовой стрелке. Фазовая траектория периодического движения замкнута, потому что система возвращается в исходное механическое состояние после каждого цикла

колебаний.

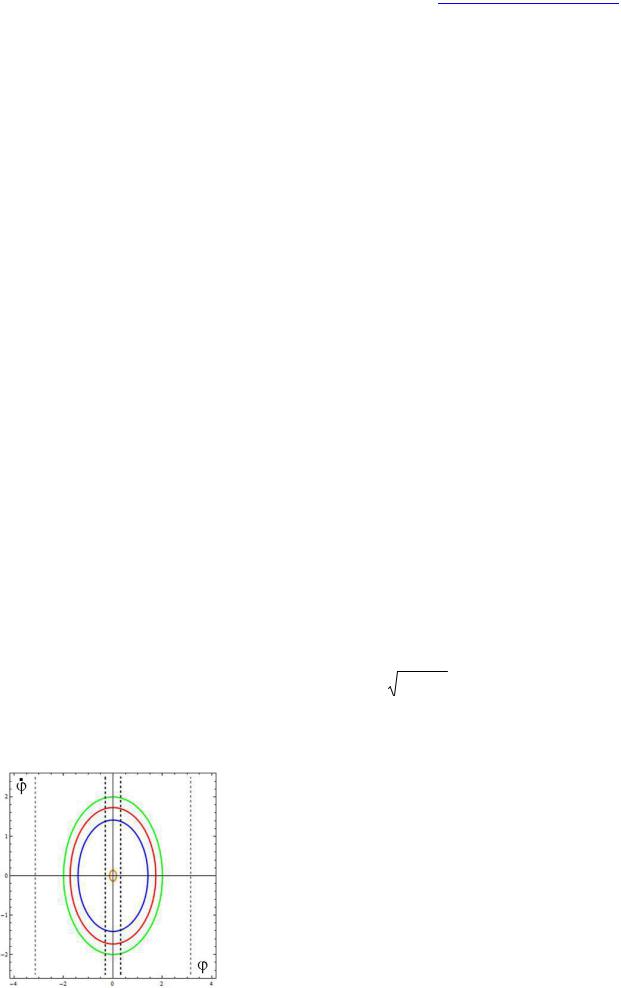
Рис. 28. Фазовый портрет затухающего линейного осциллятора (a) и системы со сверхкритическим затуханием γ>ω0 (b).

Обычно выбрано такое взаимное расположение фазовой плоскости и графика

http://profbeckman.narod.ru/

зависимости потенциальной энергии от угла отклонения, чтобы было удобно в каждый момент времени сопоставлять движущуюся по фазовой плоскости изображающую точку с выводимыми одновременно на график значениями полной энергии осциллятора. Для этого масштабы на фазовой диаграмме и на графике потенциальной энергии выбирают одинаковыми. Совокупность фазовых траекторий, соответствующих разным способам возбуждения (разным начальным условиям) при неизменных параметрах системы образует ее фазовый портрет.

Фазовый портрет консервативного линейного осциллятора образован набором геометрически подобных эллипсов с общим центром в начале координат фазовой плоскости. Этот центр изображает состояние покоя осциллятора в положении равновесия. Так как через начало координат не проходит ни одна из фазовых траекторий (все траектории окружают эту точку), такая точка фазовой плоскости называется особой точкой типа центр. Период гармонических колебаний целиком определяется параметрами физической системы. В отличие от амплитуды и начальной фазы, период не зависит от начальных условий, т. е. от способа возбуждения колебаний. Это свойство линейного осциллятора называется изохронностью. Благодаря свойству изохронности изображающие точки обходят эллипсы разных размеров на фазовом портрете осциллятора (соответствующие разным амплитудам колебаний осциллятора с данными параметрами) в течение одного и того же времени T0.

Вприсутствии сравнительно слабого вязкого трения (γ<ω0) максимальные отклонения, как и максимальные значения угловой скорости, постепенно уменьшаются с каждым последующим циклом колебаний. Поэтому фазовая траектория собственных колебаний благодаря трению трансформируется из замкнутой кривой (эллипса или окружности) для консервативного осциллятора в постепенно скручивающуюся спираль, сжимающиеся витки которой наматываются вокруг фокальной точки, расположенной в начале координат фазовой плоскости. В этом случае начало координат из особой точки типа центр превращается в особую точку типа фокус. Для семейства фазовых траекторий фокус представляет собой аттрактор: все фазовые траектории, независимо от того, где они начинаются, асимптотически приближаются к фокусу, совершая вокруг него бесконечное число оборотов по все более сжимающимся виткам (рис. 28а).

Вслучае сравнительно сильного вязкого трения (γ>ω0) аттрактор фазовых траекторий из фокуса превращается в особую точку типа узел: все фазовые траектории неколебательных движений приближаются к этому узлу напрямую без наматывания, не совершив и одного оборота. Фазовый портрет передемпфированной системы показан на рис. 28б. Все фазовые траектории асимптотически приближаются к началу координат, где

прямолинейной фазовой траектории 1 . При специфических начальных условиях вида 0 1 0 изображающая точка движется к узлу непосредственно вдоль этой прямолинейной фазовой траектории (общей касательной всех траекторий). Другая прямолинейная фазовая траектория 2

соответствует движению при начальных условиях типа0 1 0 .

Рис. 29. Фазовая диаграмма маятника в линейном режиме без трения. Зависимость скорости от угла.

Таким образом, на фазовом портрете линейного осциллятора имеется только одна особая точка: начало координат фазовой плоскости, где обе динамические

переменные и равны нулю. Этой точке

http://profbeckman.narod.ru/

соответствует состояние покоя в положении равновесия. При =0 это точка типа центр, через которую не проходит ни одна траектория. При γ<ω0 это фокус, а при γ ω0 это узел фазовых траекторий.

Рис. 30. Движение маятника, как пример фазового пространства.

Способы введения понятия "аттрактор" в описание динамических систем проиллюстрируем на примере простейшего (гармонического) осциллятора - маятника.

Гармонический осциллятор (в

классической механике) – система, которая при смещении из положение равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно

закону Гука): F=-kx, где k – коэффициент жёсткости системы.

Если F – единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение – синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего

осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Рис. 31. Фазовая диаграмма маятника в нелинейном режиме без трения.

Сначала займёмся свободными колебаниями.

Примером простой консервативной системой с одной степенью свободы является маятник.

Начнём с простого примера – малых колебаний (так же называемых гармоническими). Малые колебания встречаются почти в каждой сфере естественных наук. Для определённости, будем рассматривать колебания металлического стержня, подвешенного за один из концов (частный случай так называемого физического маятника). Можно показать, что его колебания описываются следующим дифференциальным уравнением:

где – угол отклонения стержня от вертикали, коэффициент перед синусом зависит от размера и массы стержня.

Если амплитуда (размах) колебаний достаточно мала, синус можно приближенно заменить его аргументом. В таком случае, уравнение принимает вид:

Тогда закон сохранения энергии превратился в уравнение кривой на плоскости ( , ). На рис. 31 разные значения Е представлены разными кривыми.

Каждая из полученных линий называется фазовой траекторией. Когда меняется состояние системы, изображающая её точка движется по одной из этих траекторий. По графику видно, что значения скорости и координаты меняются циклическим образом, то есть периодически повторяются. Отсюда можно сделать вывод, что описываемая рассмотренным уравнением система будет совершать колебания. Именно так ведёт себя маятник, и если решить уравнение, решение будет иметь вид периодических функций (а именно – комбинации синуса и косинуса).

Однако замена синуса его аргументом оправдана лишь для малых углов отклонения (от 10 градусов и меньше), поэтому нельзя доверять тем траекториям, которые выходят за границы области, ограниченной жирными пунктирными линиями, то есть из четырёх приведённых траекторий лишь оранжевая достоверно отображает реальность. Кроме того, поскольку это угол, то его значения, соответствующие 180 и -180 градусам описывают одно и то же положение маятника, т.е. правая и левая пунктирные линии (тонкие) на графике это на самом деле одна и та же линия.

Рис. 33. Колебание маятника в линейном (а) и нелинейном (б) режимах.

Учтём теперь нелинейность системы. Вернёмся к самому первому уравнению – с синусом проделаем с ним те же операции, что и с линейным уравнением. Тогда

Рис. 31 демонстрирует, при малых энергиях (оранжевая и синяя траектории) существует колебательный режим, но колебания уже не являются гармоническими – фазовые траектории уже не имеют форму эллипсов. При больших энергиях (зелёная траектория) колебаний уже нет, вместо этого мы получаем вращательное движение с переменной скоростью. И действительно, если достаточно сильно «толкнуть» стержень, он будет вращаться вокруг некоторой точки, замедляясь при подъёме и ускоряясь при спуске. При определенном промежуточном значении энергии получается особый набор траекторий, которые отделяют друг от друга области соответствующие разным типам движения и поэтому называются сепаратрисами. Каждая ветвь сепаратрисы это траектория, соответствующая особому типу движения. Движение начинается с очень маленькой скоростью от одного крайнего положения стержня, при приближении к положению равновесия скорость растёт, а после изображающая точка все более замедляясь, уходит к крайнему положению, где и останавливается. Это соответствует тому, что мы поднимаем стержень вертикально вверх и отпускаем его, проносясь через положение равновесия, он поднимается к верхней точке с другой стороны и останавливается.

Колебания в линейном случае происходят синхронно – с одной и той же частотой. В нелинейном же случае, частота колебания с большей амплитудой (синяя линия) оказывается меньше, чем у колебания с малой амплитудой (оранжевая линия). Это служит еще одним подтверждением того, что нелинейные колебания не являются гармоническими.

Рис. 34. Движение по кругу и движение гармоническое.

Эллиптические кривые на рис. 31 соответствуют устойчивым процессам (нижнее положение равновесия маятника), а гиперболические точки, соответствующие

верхнему положению равновесия маятника, являются неустойчивыми. Фазовая кривая, начавшаяся в окрестности гиперболической точки, удаляется от неё, в то время как траектория вблизи эллиптической точки всегда остаётся в её окрестности.

Замечание. Маятник в случае малых отклонений описывается линейными уравнениями: частота колебаний не зависит от амплитуды. Маятник в случае больших отклонений относится к нелинейной системе: частота колебаний зависит от амплитуды.

В качестве другой модели консервативного гармонического осциллятора возьмём груз массы m, закреплённый на пружине жёсткостью k.

Пусть x – смещение груза относительно положения равновесия. Тогда, согласно закону Гука, на него будет действовать возвращающая сила:

F=-kx. (8)

Используя второй закон Ньютона, запишем a k .

Обозначая 02 k и заменяя ускорение a на вторую производную от координаты m

http://profbeckman.narod.ru/

Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Коэффициент 0 называют циклической частотой осциллятора. (Здесь имеется в виду круговая частота, измеряющаяся в радианах за секунду. Чтобы перевести её в частоту, выражающуюся в герцах, надо разделить

(12)

Амплитуда сокращается. Значит, она может иметь любое значение (в том числе и нулевое – это означает, что груз покоится в положении равновесия). На синус также можно сократить, так как равенство должно выполняться в любой момент времени t. Таким образом, остаётся условие для частоты колебаний: - 2+ 02=0, =+0.

Отрицательную частоту можно отбросить, так как произвол в выборе этого знака покрывается произволом выбора начальной фазы.

x(t)=Asin(0+ 0) (13)

где амплитуда A и начальная фаза φ0 – произвольные постоянные.

Эта запись исчерпывает все решения дифференциального уравнения, т.к. позволяет удовлетворить любым начальным условиям (начальному положению груза и его начальной скорости).

Как уже упоминалось, точечный аттрактор - аттрактор, для которого все траектории в фазовом пространстве сходятся к одной точке или величине. Важно, что любая система, которая стремится к одному устойчивому состоянию равновесия, будет иметь точечный аттрактор. Маятник с трением всегда остановится. Его фазовое пространство "стягивается" в точку, где скорость и координаты равны нулю.

Рис. 35. Положение, скорость и ускорение простого гармонического движения на фазовой плоскости.

Таким образом, консервативный гармонический осциллятор может совершать чисто гармонические колебания с частотой, равной его собственной частоте, с амплитудой любой величины и с произвольной начальной фазой.

Кинетическая энергия записывается в виде

тогда полная энергия имеет постоянное значение

2

Простое гармоническое движение – это движение простого гармонического осциллятора, периодическое движение, которое не является ни вынужденным, ни затухающим. Тело в простом гармоническом движении подвергается воздействию единственной переменной силы, которая по модулю прямо пропорциональна смещению x от положения равновесия и направлена в обратную сторону. Это движение является

http://profbeckman.narod.ru/

периодическим: тело колеблется около положения равновесия по синусоидальному закону. Каждое последующее колебание такое же, как и предыдущее, и период, частота и амплитуда колебаний остаются постоянными. Если принять, что положение равновесия находится в точке с координатой, равной нулю, то смещение x тела от положения равновесия в любой момент времени даётся формулой:

x(t)=Acos(2 ft+ 0), (17)

где A – амплитуда колебаний, f – частота, φ – начальная фаза, =2 f – круговая частота Частота движения определяется характерными свойствами системы (например,

массой движущегося тела), в то время как амплитуда и начальная фаза определяются начальными условиями – перемещением и скоростью тела в момент начала колебаний. Кинетическая и потенциальная энергии системы также зависят от этих свойств и условий.

Рассмотрим теперь гармонический осциллятор с затуханием.

Затухающие колебания – колебания, энергия которых уменьшается с течением времени.

Маятник является простым примером динамической системы с двумя факторами, которые определяют его движение: скорость и положение. Вычерчивание кривой скорости или положения против времени привело бы к простой синусоидальной волне, или гармоническому осциллятору, поскольку положение и скорость поднимаются и падают по мере того, как маятник движется вперед и назад, поднимаясь и падая. Однако при создания графика скорости от положения, удаляется время как измерение. Если нет трения, маятник будет качаться назад и вперед вечно, и его фазовая диаграмма будет представлять собой замкнутый круг. Однако если имеет место трение или затухание, то при каждом колебании маятника назад и вперед, он движется немного медленнее, и его

амплитуда уменьшается, пока он, в конце концов, не останавливается. Соответствующая фазовая диаграмма будет постепенно снижаться до начала координат, где скорость и положение приходят к нулевому значению.

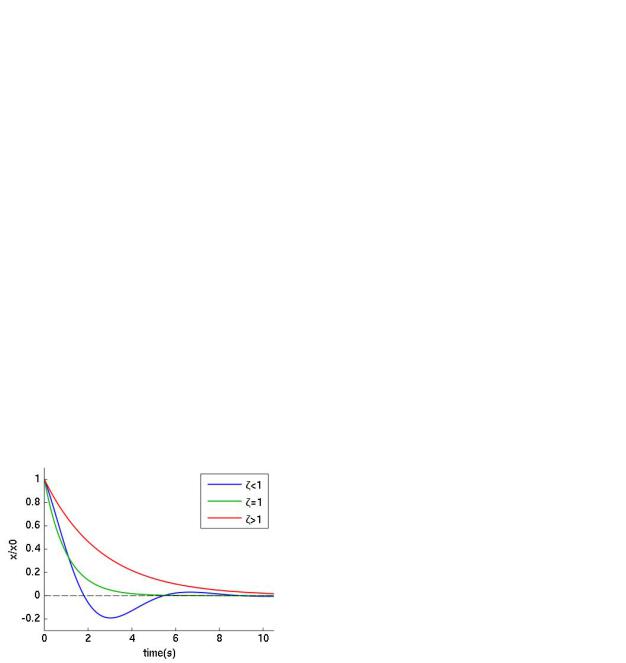
Рис. 36. Зависимость графиков колебаний от значения коэффициента затухания.

Бесконечно длящийся процесс вида u(t)=Acos( t+ ) в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются.

Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний или её квадрата. Свободные колебания реальных систем всегда затухают. Затухание обусловлено трением (механические системы) и сопротивлением (в электромагнитных колебательных контурах).

Примером осциллятора с затуханием служить маятник, колебания которого затухают из-за вязкого трения. Сила вязкого трения направлена против скорости движения груза относительно среды и прямо пропорциональна этой скорости. Тогда полная сила, действующая на груз, записывается так:

http://profbeckman.narod.ru/

приведен фазовый портрет системы, описывающей колебания математического маятника без трения ("кошачий глаз", на нижнем – колебания математического маятника "с трением".

Под автоколебаниями понимают колебательный процесс в диссипативных системах (т.е. в системах с потерями задействованной в процессе энергии – на трение, выделение тепла), характеристики которого – амплитуда колебаний, их форма, период и частота (в более общем случае – спектр) определяются самой системой и не зависят от изменения начальных условий. Образ автоколебаний в фазовом пространстве – аттрактор

– фазовая траектория или множество траекторий, к которому притягиваются все близлежащие траектории. Аттрактор, отвечающий периодическим автоколебаниям, есть замкнутая фазовая траектория – предельный цикл.

Самая древняя автоколебательная система – маятниковые часы. Гиря на цепочке стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается, но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.