http://profbeckman.narod.ru/

незначительно отличается от предыдущего, невозможно предсказать, где оно окажется после итераций.

Для случая r>r справедлива теорема Фату: если квадратичная функция имеет устойчивую периодическую орбиту, то критическая точка находится в устойчивом множестве точек этой орбиты (при повторении критической точки, она попадет в аттрактор (если он существует)). Критическая точка – это точка, где производная равна нулю. В логистическом отображении критическое значение всегда равно 0,5. Именно этот факт позволяет построить бифуркационную диаграмму.

19.5 Бифуркационная диаграмма логистического отображения

Каскад бифуркаций удвоения периода в логистическом отображении можно наглядно представить на фазопараметрической диаграмме (однопараметрическая бифуркационная диаграмма, дерево Фейгенбаума). Бифуркационное дерево даёт зависимость установившихся значений переменной x от параметра r. Начальный участок дерева представлен на

рис. 21 и рис.22.

Рис. 21. Бифуркация типа вилки.

Это неустойчивая неподвижная точка и рождающийся 2-цикл. В последнем случае переменная последовательно посещает две ветви дерева. Такую

ситуацию называют бифуркацией удвоения периода.

Полное дерево (для всех значений параметра) строят численно с помощью компьютера. Для этого сначала задают некоторое начальное значение переменной х0 и параметра r. Затем выполняют несколько сот итераций отображения, чтобы исключить переходные процессы и реализовать установившийся режим. Потом процедуру повторяют для слегка измененного количества параметра (в качестве нового начального значения переменной использовать то, что получилось на предыдущем шаге процедуры). И,

наконец, всё повторяют для всего диапазона управляющего параметра. На графике по оси х задаётся диапазон изменений управляющего параметра r (от 0 до 4), а на оси y – положение предельных точек отображения (принимаемые при больших временах значения x).

Рис. 22. Начальная стадия бифуркаций типа вилка при эволюции логистического отображения. Последовательные бифуркации разделяются расстоянием, причём фактор d асимптотически уменьшается при росте r. Это справедливо для широкого класса отображений, причём

для них значение d одинаково. При росте r число бифуркаций увеличивается.

Стабильная точка равна 0, и поэтому кривая на отрезке 0 r<1 лежит точно на оси х. Между 1 и 3 функция имеет одну стабильную точку (гладкая возрастающая кривая). При увеличении r (r>3) отображение имеет две устойчивые неподвижные точки: одну из точек где-то между 0 и 0,5, другая – где-то между 0,5 и 1 (устойчивая орбита). После другой бифуркации оно имеет стабильную орбиту периода четыре. Постепенно расстояние между точками бифуркации становится короче и короче. Периода 8 аттрактор ещё в видим, но орбита с периодом 16 почти нет, а период 32 исчез в затемнённой массе.

Затемнённый беспорядок – это хаос, входящий в систему. После r итерация критической точки больше не попадает в хороший стабильный аттрактор. Она мечется, как муха. Это область хаотических орбит. Хаотические орбиты непериодические (они никогда не повторяются) и не являются бассейном периодического аттрактора. Важно, что

http://profbeckman.narod.ru/

они чувствительны к начальным условиям, т.е. значит, что ближайшие друг к другу орбиты быстро разойдутся в разные стороны.

Примечательная особенность (рис. 23) – наличие вертикальных полос, пересекающих район хаоса. Это – зоны периодических орбит. Удивительно, но при росте параметра r в среде сплошного хаоса возникают зоны порядка и устойчивости. Причём таких зон несколько. Существует устойчивый периодический аттрактор, сколь угодно близкий к любой хаотическому аттрактору!

Бифуркационная диаграмма отчетливо демонстрирует бифуркацию из устойчивой неподвижной точки на устойчивую орбиту 2-цикла при r=3, а затем бифуркацию от 2- цикла к 4-циклу при r между 3.4 и 3.5. Дальнейшие удвоения периода происходят при уменьшении приращений в r, а орбита становится хаотичной при r 3.57. При r=3,83 третье итерированное отображение имеет 8 неподвижных точек: {0}, {0,156149}, {0,16357}, {0,504666}, {0,524001}, {0,738903}, {0,955294} и {0,957417}. Две из них – неустойчивые неподвижные точки основного отображения. Остальные шесть оказываются компонентами двух периодов 3-цикла, одна устойчивая и одна неустойчивая.

Устойчивые орбиты: 0,1556149, 0,504666 и 0,957417, неустойчивые: {0.16357, 0.524001 и 0.955294}. Удивительный эффект наблюдается при небольшом превышении r значения 3.8. При r=3.83 возник 3-цикл! Устойчивый периодический цикл с тремя строго стабильными неподвижными точками: 0,50466; 0,957414 и 0,156149.

На рис. 23 хорошо видны точки бифуркаций удвоения периода, когда каждая ветвь бифуркационного дерева расщепляется на две. При достаточно больших значениях параметра r наблюдается большое количество точек по оси ординат x, которые соответствуют хаотическому режиму. Области хаоса чередуются с так называемыми «окнами периодичности (или устойчивости)», в которых реализуются периодические режимы − циклы различных периодов. Появление циклов в закритической области, а,

следовательно, и окон периодичности, определяется порядком Шарковского: 3→5→7→3 2 5 2 7 2 ... 3 22→5 22→7 22→...→23→22→2→1. (33)

Рис. 23: Фазопараметрическая диаграмма для логистического отображения (1)

(зависимости числа особей от скорости роста популляции). Внутри режима хаоса можно найти

бесконечное число всё уменьшающихся областей значений r, для которых система вновь становится периодичной (белые вертикальные полосы).

http://profbeckman.narod.ru/

Рис. 24. Бифуркационная диаграмма рис.9 при сильном увеличении.

В (8) цифры означают периоды циклов отображений, а 2 − тот факт, что этот цикл претерпевает каскад бифуркаций удвоения периода.

При анализе рис. 23 можно сделать следующие выводы:

−при некоторых значениях r=rn управляющего параметра происходит бифуркация, в результате которой каждая предельная точка отображения fr распадается на две;

−при n-й бифуркации число предельных точек становится равным 2n;

−при r>r∞ интервалы значений параметра r, при которых наблюдается сплошное заполнение отрезка [0,1] предельными точками «логистического» отображения, изредка сменяются периодами порядка, когда число предельных точек вновь конечно.

При превышении параметра r значения r=3,0 возможные изменения численности популяции по бифуркации типа вилка могут происходить по двум дискретным путям. При r=3,2 система заметно колеблется относительно двух значений популяции: одно около 0,5, а другое около 0,8. При таком значении r применение логистического уравнения к одному из этих значений дает другое. Сразу после r=3,4 диаграмма снова раздваивается, делая вероятными четыре пути, система колеблется относительно четырех значений популяции. Сразу после r=3.5 снова следует раздвоение, давая восемь путей. Здесь система осциллирует относительно восьми базовых значений числа особей.

После r=3,6, бифуркации растут до тех пор, пока система в конечном итоге не достигнет любого значения. Это путь к хаосу через удвоение периода. По мере увеличения r логистическое отображение колеблется сначала между двумя, затем четырьмя, восемью, 16, а затем 32 значениями. Это периоды подобны периоду колебания маятника. Картина в увеличенном масштабе (на участке от r=3,7 до r=3,9) приведена на рис. 24.

При приближении к хаосу из шума возникают странные закрученные узоры и пороги, с каждой стороны которых система ведет себя совершенно различно. Между параметрами r=3,82 и r=3,84 система переходит из хаоса обратно в порядок, колеблется между тремя значениями популяции (приблизительно 0,15, 0,55 и 0,95). Но затем пути снова раздваиваются и выше r=3,86 система возвращается к хаосу.

Диаграмма, подобная (рис. 23) характерна для всех систем с каскадом удвоений периодов, приводящим к хаосу.

Как уже упоминалось, структура бифуркационной диаграммы самоподобна: если увеличить область, к примеру, при значении rс=3.82 в одном из трех ответвлений, то можно увидеть, что тонкая структура этой области выглядит, как искаженная и размытая версия всей диаграммы. То же самое верно для любой окрестности нехаотических точек. Это пример глубокой связи между хаотическими системами и фракталами. Рассматриваемая здесь структура фрактальна со странным аттрактором (см. далее). При сильном увеличении (рис. 24) видны меньшие копии большей макроструктуры: есть

http://profbeckman.narod.ru/

повторение тех же бифуркаций, хаоса и предельных циклов, которые видели на первой диаграмме (рис. 23) бифуркации полного диапазона изменения параметра r.

Рис. 25. Бифуркационная диаграмма логистического отображения: участок в районе r = 3,5 (значение, при котором сначала появляется 2n-цикл, обозначенный синими линиями).

19.6 Цикл периода 3

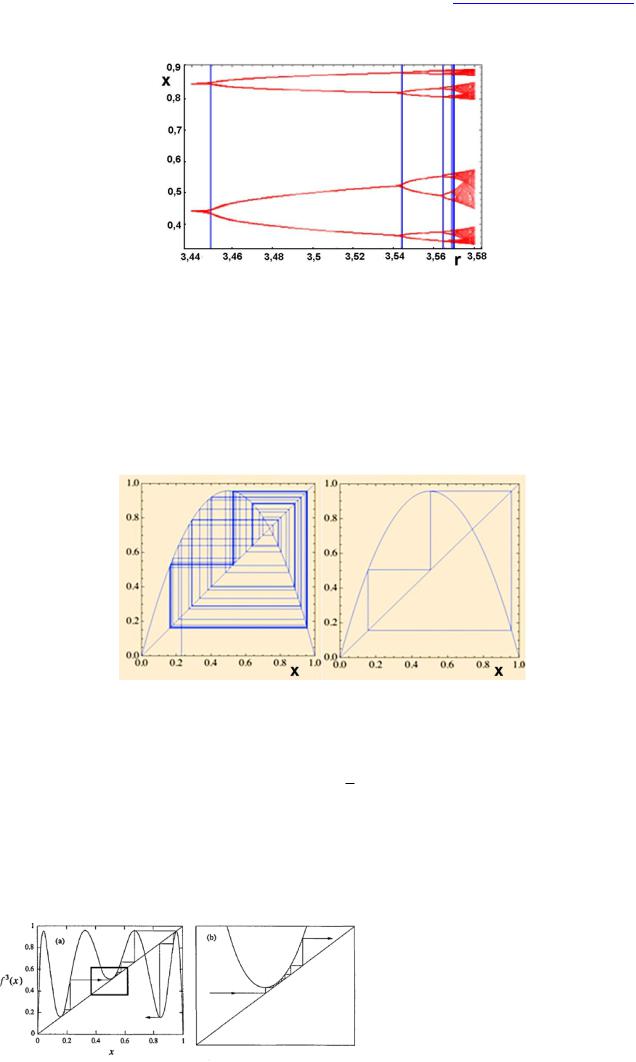
Возникновение среди хаоса упорядоченного цикла – удивительный и важный эффект: из его существования следует возможность циклов любого периода. Самое широкое окно устойчивости имеет цикл периода 3). 3-цикл возникает в результате касательной бифуркации. Он ростом параметра r претерпевает последовательность бифуркаций удвоения периода. На рис. 25 показан увеличенный фрагмент бифуркационной диаграммы (рис. 24), соответствующий окну периодической устойчивости цикла периода 3.

Рис. 26. Переход к 3-циклу (периодическая орбита) при r=3,83.

Для нахождения значений r, при которых существует 3-цикл, решают уравнение f(х(f(x)))=x, в котором f(x)=rx(1-x), находя значения r, для которых третья итерация f(x) пересекает диагональ 45°. Две неподвижные точки очевидны: 0 и 1-1/r. Они имеют период 1, поэтому имеют и период 3 (что фиксируется после одной итерации остается

фиксированным и после трех). Но при r 1 8 3,828... существует еще одна орбита 3 орбита, причём устойчивая. Самое интересное явление наблюдается в районе, расположенном непосредственно перед периода три окном. График f(x) почти затрагивает диагональ. Здесь ключевое слово почти. При большем увеличении видно, что при приближении к точке касания, в которой появляется стабильный период три, график сжимается в небольшое пространство между графиком f3(x) и диагональю. Прохождение узкого канала требует большого количества итераций.

При касании f3(xn)≈xn. При удалении r от периодического окна прерывистость уменьшается пока не

http://profbeckman.narod.ru/

будет достигнуто полное хаотическое поведение. Это путь к хаосу через перемежемость. При r>rс существуют неустойчивые 2n-циклы для всех n.

Рис. 27. Графический анализ третьей итерационной функции логистического отображения в точке перехода (r=3,828): а – исходный масштаб; б – увеличенный масштаб. Касательная бифуркация, перемежаемость (интермитанс).

Рис. 28. Путь к хаосу через перемежаемость при r=3,8282..

Стабильный 3-цикл располагается в окне от 3.8284 ... до 3.8415 .... Когда 3-цикл становится неустойчивым, возникает бифуркация удвоения периода, и стабильный 6-цикл. Возможен устойчивый (3×2n) -цикл для всех n: если одну ветвь стабильного 3- цикла увеличить, снова появится орбитальная диаграмма в миниатюре, т.е. диаграмма имеет фрактальную структуру. Теперь мы рассмотрим выбор r чуть ниже периодического

окна. Рис.28 показывает типичную орбиту для r=3,8282. Орбита почти образует 3-цикл с вкрапленными периодами хаоса. Это явление называется прерывистостью (интермитанс).

В виду важности 3-цикла рассмотрим его появление несколько подробнее. Обозначим третью итерацию как f3(x), а точку периода 3 орбиты р как p=f3(p) Функция

у=f3(x) восемь раз пересекает диагональную линию (y=x). При уменьшении rc 1 8 устойчивые и неустойчивые 3-циклы столкнутся и будут иметь одинаковые значения x.

Условие касательной бифуркации может быть выражено касанием у=f3(x) к прямой у=х. Для определения устойчивости орбиты найдём производную от отображения.

Нужно найти комбинацию a+b+c, ab+bc+ac и abc, но не a, b, c индивидуально.

Рис. 29. График f3(x) для rс=3,85. Зачернённые кружки – устойчивый 3-цикл, пустые кружки

– неустойчивый 3-цикл. заполненные квадраты – неподвижные точки f3(х).

Третья итерация f(x) имеет неподвижную точку в x=a, b и c. Введём вспомогательную функцию g(x)=f3(x)-x, которая имеет корни в фиксированных точках f(x). Для r, большего, чем rc, функция g(x) имеет восемь вещественных корней. (g(x) – многочлен

восьмого порядка, f3(x) – третья итерация квадратичной функции). При r=rc значения x для устойчивого и неустойчивого 3-цикла смыкаются при a, b и c. Функция g(x) имеет двойные корни в a, b, c. Это составляет шесть из восьми корней g. Поскольку две дополнительные неподвижные точки f находятся в точке х=0 и х=1-1/r, то

g(x) x(x-1+1/r)[(x-a)(x-b)(x-c)]2. (36) g(x) x8-[2 +1-1/r]x7+[2 + 2+2(1-1/r) ]x6-[2 -2 +2(1-1/r) +(1-1/r) 2]x5+... (37)

где