
- •Аннотация
- •От автора
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •1. СИСТЕМЫ И ПРОЦЕССЫ
- •2. ПОРЯДОК, НЕПОРЯДОК, БЕСПОРЯДОК И ХАОС
- •3. ТЕРМОДИНАМИКА
- •3.1 Начала термодинамики
- •3.2 Равновесная термодинамика
- •4. НЕРАВНОВЕСНАЯ ТЕРМОДИНАМИКА
- •4.1 Диссипативные структуры, системы и среды
- •4.2 Термодинамика необратимых процессов
- •4.3 Линейная неравновесная термодинамика
- •4.4 Нелинейная неравновесная термодинамика
- •4.5 Статистическая термодинамика
- •5. ЭНТРОПИЯ
- •5.1 Определение и свойства энтропии
- •5.2 Энтропия в химической термодинамике
- •5.3 Энтропия в статистической физике
- •5.3.1 Энтропия Больцмана-Планка
- •5.3.2 Энтропия Гиббса
- •5.4 Тсаллис (Цаллис) энтропия (Революция в термодинамике)
- •6. ГЕОМЕТРИЯ ФРАКТАЛОВ
- •6.1 Элементы геометрии фракталов
- •6.2 Размерности фракталов
- •6.3 Примеры фракталов
- •6.4 Фракталы и энтропия
- •7. ИНФОРМАТИКА
- •7.1 Информация, информатика и информационные технологии
- •7.2 Теория информации
- •7.2.1 Информация Хартли
- •7.2.2 Энтропия Шеннона
- •7.3 Отрицательная энтропия, антиэнтропия, экстропия
- •7.4 Алгоритмическая теория информации
- •7.4.1 Энтропия Колмогорова
- •7.4.2 Эпсилон-энтропия
- •7.5 Энтропия Кульбака-Лернера
- •7.6 Энтропия Реньи
- •7.7 Квантовая информатика
- •7.7.1 Некоторые положения квантовой механики
- •7.7.2 Энтропия фон Неймана
- •7.7.3 Линейная энтропия
- •7.7.4 Сравнение энтропий Реньи, Цаллиса и Неймана
- •7.7.5 Энтропия Холево
- •8. СИНЕРГЕТИКА
- •8.1 Синергизм и синергетика
- •8.2 Детерминизм, случайность и неопределённость
- •8.3 Простые и сложные системы
- •8.4 Анализ систем
- •8.5 Параметры порядка (управляющие параметры)
- •8.6 Процессы самоорганизации
- •9. СИСТЕМЫ И ЗАКОНЫ ИХ ЭВОЛЮЦИИ
- •9.1 Статические системы
- •9.2 Динамические системы
- •9.3 Линейные динамические системы
- •9.4 Нелинейные динамические системы
- •9.5 Эволюция динамической системы
- •9.6 Математическое описание эволюции динамической системы
- •10. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ОПИСАНИИ ДИНАМИЧЕСКИХ СИСТЕМ
- •10.1 Обыкновенные дифференциальные уравнения
- •10.2 Фазовое пространство и пространство состояний
- •10.3 Линейные ОДУ на плоскости
- •10.4 Нелинейные дифференциальные уравнения
- •11. ОТОБРАЖЕНИЯ
- •11.1 Системы с дискретным временем в отображениях
- •11.2 Итерации в исследовании динамических систем
- •11.3 Графические методы нахождения неподвижных точек и исследования их свойств
- •11.4 Многопараметрические отображения
- •11.5 Примеры некоторых важные отображений
- •12. ОСОБЫЕ ТОЧКИ ФАЗОВЫХ ПОРТРЕТОВ ДИНАМИЧЕСКИХ СИСТЕМ
- •12.1 Дифференциальные уравнения и особые точки
- •12.2 Классификация точек равновесия
- •12.3 Фазовые портреты и особые точки нелинейных ОДУ
- •12.4 Многомерные системы
- •13. РЕГУЛЯРНЫЕ АТТРАКТОРЫ И РЕПЕЛЛЕРЫ
- •13.1 Типы аттракторов
- •13.2 Фазовый объём
- •13.3 Репеллеры
- •13.4 Осциллятор и осцилляции
- •14. УСТОЙЧИВОСТЬ ДИНАМИЧЕСКИХ СИСТЕМ
- •14.1 Устойчивые и неустойчивые равновесия
- •14.2 Устойчивость по Ляпунову (метод первого приближения)
- •14.3 Показатель Ляпунова
- •14.4 Устойчивость нелинейной системы
- •14.5 Метод функций Ляпунова
- •14.6 Функция Ляпунова и энтропия
- •14.7 Асимптотическая устойчивость
- •14.8 Устойчивость особых точек
- •14.9 Устойчивость особых точек
- •14.10 Устойчивость решений дискретных уравнений
- •15. БИФУРКАЦИИ
- •15.1 Бифуркации: основные понятия и классификация
- •15.2 Элементы теории бифуркаций
- •15.3 Простейшие бифуркации
- •16. БИФУРКАЦИИ ЦИКЛОВ
- •16.1 Предельные циклы
- •16.2 Устойчивость предельных циклов
- •16.3 Бифуркации устойчивых предельных циклов
- •16.5 Бифуркация рождения пары устойчивых замкнутых траекторий.
- •16.6 Транскритическая (обмена устойчивостью между циклами) бифуркация.
- •16.7 Бифуркация исчезновения (рождения) пары замкнутых траекторий.
- •16.8 Бифуркация удвоения периода цикла
- •16.9 Бифуркация рождения (гибели) двумерного тора.
- •16.10 Гомоклиническая бифуркация рождения/исчезновения цикла
- •17. ДИНАМИЧЕСКИЙ ХАОС
- •17.1 Хаос статистический и динамический
- •17.2 Предсказание статического поведения системы
- •17.3 Сценарии перехода к хаосу
- •17.4 Примеры систем с хаосом
- •18. ХАОС В ЛИНЕЙНЫХ ОДНОМЕРНЫХ СИСТЕМАХ
- •18.1 Бифуркационные диаграммы
- •18.2 Лестница Ламерея
- •18.3 Отображение Бернулли
- •18.4 Треугольное отображение
- •18.5 Отображение «тент»
- •18.6 Канторов репеллер
- •18.7 Детерминированная диффузия
- •19. ХАОС В ЛОГИСТИЧЕСКОМ ОТОБРАЖЕНИИ
- •19.1 Переход к хаосу через удвоение периода
- •19.2 Логистическое уравнение
- •19.3 Дискретное логистическое уравнение
- •19.4 Логистическое отображение
- •19.5 Бифуркационная диаграмма логистического отображения
- •19.6 Цикл периода 3
- •19.7 Фазовые диаграммы логистического отображения
- •19.8 Аттракторы и фракталы в логистическом отображении
- •20. ХАОС В НЕЛИНЕЙНЫХ ОДНОМЕРНЫХ ОТОБРАЖЕНИЯХ
- •20.1 Отображение xn+1=С+xn2.
- •20.2 Отображение xn+1=а-xn2.
- •20.3 Подобие окон периодической динамики
- •20.4 Порядок Шарковского
- •20.5 Универсальность Фейгенбаума
- •20.6 Устойчивость циклов одномерных отображений
- •20.7 Топологическая энтропия
- •20.8 Синус-отображение
- •21. ХАОС В НЕЛИНЕЙНЫХ ДВУМЕРНЫХ ОТОБРАЖЕНИЯХ
- •21.1 Отображение Эно (Henon map)
- •21.2 Отображение подковы и отображение пекаря
- •21.3 Отображение «кот Арнольда» (Arnold’s cat map)
- •22. НЕРЕГУЛЯРНЫЕ АТТРАКТОРЫ
- •22.1 Хаос в консервативных и диссипативных системах
- •22.2 Регулярные и хаотические аттракторы
- •22.3 Квазиаттракторы
- •22.4 Хаотически аттракторы
- •22.5 Негиперболические хаотические аттракторы
- •22.6 Фрактальные аттракторы
- •22.7 Характеристика нерегулярных аттракторов
- •22.8 Странные нехаотические аттракторы
- •22.9 Сингулярные аттракторы
- •22.10 Многомерные нерегулярные аттракторы
- •22.11 Дикие аттракторы
http://profbeckman.narod.ru/
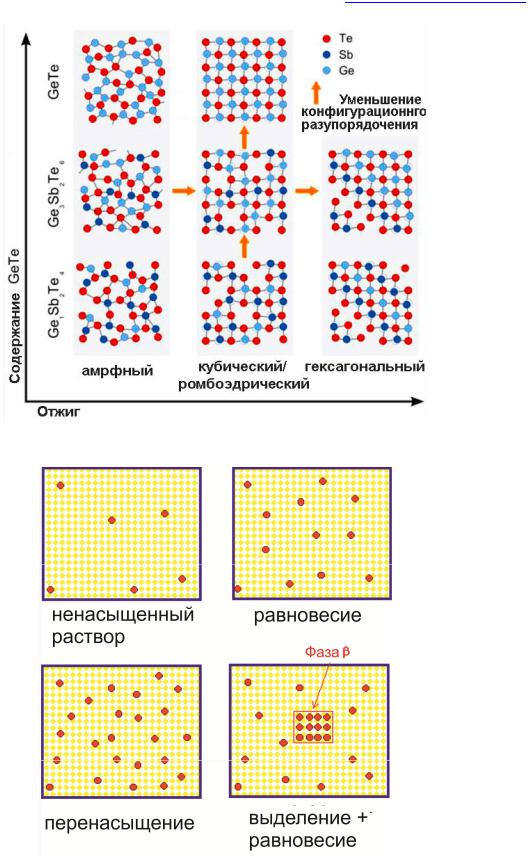
Рис. 8. Изменение расположения ионов в твёрдом теле при последовательных переходах:
аморфное тело кристалл типа 1кристалл типа 2. Возникновение порядка из беспорядка.
Рис. 9. Рост кристалла из раствора – возникновение порядка из беспорядка.
5.4 Тсаллис (Цаллис) энтропия (Революция в термодинамике)
Энтропия Цаллиса – обобщение стандартной энтропии Больцмана-Гиббса.
Как уже упоминалось, основные свойства термодинамической энтропии: её экстенсивность и аддитивность

|
|
|
|
http://profbeckman.narod.ru/ |
||
S(A+B) = S(A) + S(B). |
|
|
|
(55) |
|
|
В статистической физике показывается, что энтропия является аддитивной |
||||||
величиной и принимает максимальное значение в состоянии равновесия. |
|
|||||
Это |
справедливо, |
если |
силы между |
частями |
системы |
являются |
короткодействующими: каждая молекула чувствует лишь несколько ближайших соседей. Однако, существуют системы, которые не могут быть описаны больцмановской
термодинамикой. Прежде всего, это системы с сильными корреляциями, с сильными и дальнодействующими взаимодействиями между всеми частями системы, с эффектами памяти (система помнит свое прошлое – эволюция системы в данный момент времени зависит не только от параметров системы в этот конкретный момент времени, но и от ее параметров некоторое время назад). Типичным примером являются квазичастицы и фононные колебания в кристалле. В этих случаях предположение молекулярного хаоса, лежащее в основе больцмановского выражения для энтропии, не выполняется.
Константино Тсаллис (Constantino Tsallis, грек из Бразилии, в русской литературе называется Цаллис) в 1988 в рамках статистической термодинамики предложил обобщение энтропии Больцмана-Гиббса на случай неаддитивных систем. Его гипотеза базируется на предположении, что сильное взаимодействие в термодинамически аномальной системе приводит к новым степеням свободы, к совершенно иной статистической физике не-больцмановского типа, т.е. отдельные частицы с больцмановской статистикой + сильное взаимодействие => новые степени свободы с небольцмановской статистикой + отсутствие взаимодействия. Эта гипотеза не доказана, но оказалась полезной для ряда приложений.
Цаллис теоретическим обоснованием своей гипотезы особенно не заморачивался. Он просто взял стандартное выражение для энтропии, а логарифм заменил на степенную функцию
ln x logq x x1 q 1
1 q |
(56) |
|
с неким числовым параметром q (действительное число, энтропийный индекс, мера неэкстенсивности системы).
Цаллис подбирал формулу для энтропии, которая переходила бы в стандартную формулу в пределе слабой связи и описывала неэкстенсивные системы. Физический смысл ей придали намного позже.
q-Энтропия Цаллиса (дискретный случай) задаётся формулой:
|
|
|
|
|
q |
|
|
|
|
|
|
|
||
|
|
|
|
k 1 pi |
|
|
|
|
x |
|
|
|
||
|
|
q |
ln q pi |
|
i |
|
|
|
; |
pi 1, |
(57) |
|||
Sq |
pi |
|
|
|
k Dq pi |
|||||||||
|
q 1 |
|
||||||||||||
|
|
i |
|
|
|
|
|
i |
x 1 |
|
i |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Dq |
- |
q-производная |
по х. |
Sq |
можно |
сравнить со стандартной энтропией |
||||||||
S lim |
d |
pix |
. k – размерная константа, если размерность существенна для понимания |
|||||||||||
dx |
||||||||||||||
x 1 |
i |
|
|
|
|
|
|
|
|
|
|
|
||
задачи.
При q1 – достигается энтропия Больцмана-Гиббса (и Шннона) SBG k pi ln pi
i
и S(AB)=S(A)+S(B).
Если q>1, а все pi0, кроме одного pi1 (заполнен один уровень – система полностью детерминирована), то Sq>0. Sq достигает экстремума (максимума – при q>1 и минимума – при q<1) в случае равновероятностного распределения (т.е. pi=1/N). В этом случае
Sq |
k |
N q 1 |
. |
|
|
|
|||
|
|
1 q |
(58) |
|
|
|
|
|
|

http://profbeckman.narod.ru/
При q=1, S=k lnN – известная формула Больцмана–Хартли–Шеннона для равновероятных распределений. Sq – вогнута при q>0 и выпукла при q<0, что является основой термодинамической устойчивости.
Важнейшим свойством энтропии Тсаллеса является её неаддитивность, в отличие от всех рассмотренных нами энтропий, в которых была принята аддитивная мера Хартли. Это обстоятельство позволяет описывать системы с длинной памятью, а также и такие системы, в которых каждый элемент взаимодействует не только с ближайшим соседом или несколькими ближайшими соседями, но и со всей системой вцелом или ее частями (системы с дальнодействующими силами). Примерами таких систем являются гравитируюшие системы: звездные скопления, газопылевые комплексы, галактики, скопления галактик и др.
Если две системы А и В независимы, то
Sq A B |
|
Sq (A) |
|
Sq (B) |
1 q |
Sq A Sq B |
|
(59) |
|
|
k |
k 2 |
|||||
k |
k |
|
|
|||||
При q<1 получаем сверхэкстенсивный случай, q=1 – экстенсивный и при q>1 – субэкстенсивный.
Если N состояний системы разбить на две подсистемы L и M (N=L+M) так, что
pl pL |
и pm pm ; |
pL pM 1 |
|
|
|
|
|
|||
L |
M |
|
|
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
q |
p |
q p |
m |
|
|
|||
Sq pi Sq pL , pM pL Sq |
l |
|
pM |
|
|
(60) |
||||
|
|
|
||||||||
|
|
|
pL |
pM |
|
|
||||
Эта формула обобщает формулу Шеннона.
Величина q ничем не ограничена и может принимать значения от минус бесконечности до плюс бесконечности, однако некоторые ограничения возникают в некоторых конкретных задачах. При использовании энтропии Цаллиса в информатике, константа k отбрасывается и q-энтропия становится безразмерной.
В случае непрерывного распределения
Sp p |
1 |
1 p x q dx |
|
|
|
||
|
q 1 |
(61) |
|
|
|
|
|
где р(х) – функция плотности вероятности. q-Энтропия – неэкстенсивная функция. Здесь
Sq ( A B) Sq A Sq B 1 q Sq A Sq B
(62)
Параметр |1-q| – мера неэкстенсивности системы.
Рис. 10. Зависимость распределения частиц по энергиям от абсолютной температуры при различных значениях параметра q; уравнение Гиббса (пунктир) и распределения Цаллиса. Энергия активации 100 кДж/моль, Газовая постоянная R=8,314 Дж/(моль К), Интервал температур 300 – 700К, Интервал q 0.01 – 10.
Замечание. Тот факт, что Цаллис взял степенную функцию "с потолка", никак не обосновав свой подход (почему бы не взять полином или ещё что-то не менее умное?!), помешало внедрению подобных идей в физическую химию. Неаддитивность энтропии также рассматривалась не как достоинство, а как крупный недостаток новой теории. Однако, удалось найти несколько примеров, в которых q-энтропия

http://profbeckman.narod.ru/
довольно хорошо работает (например, при описании супердиффузии). Кроме того, степенная функция спадает существенно медленнее, чем экспонента, что позволяет совместить q- энтропию с распределениями Леви-Паррето и геометрией фракталом. Обстоятельство, обеспечивающее перспективность идей Цаллиса в физической химии и информатике, особенно при описании аномальной диффузии. Оказалось, что подход Цаллиса даёт некое обобщение термодинамики, статистической физики и физической кинетики.
Переход от логарифмической к степенной функции, переводит распределение частиц по энергиям Гиббса
p(E) ~ exp(–E/kT) |
(63) |
в энергетическое распределение Цаллиса
|
|
|
|
|
|
|
E |
q |
|
|
|
E |
|
|
|
1 q |
|
||||
|
|
|
|
|||||||
p |
|
1 1 q |
|
|
(64) |
|||||
|
|
|
|
|
|
|
kT |
|||
Теперь при больших значениях энергии. При q>1 имеет место степенное, а не экспоненциальное падение вероятности в ростом энергии, при q<1 существует максимально возможная энергия Емакс (обрезка распределения), при q=1 – распределение Больцмана.
Неаддитивность энтропии Цаллиса позволяет построить новую термодинамику и новую статистическую теорию, способные просто и корректно описывать системы с длинной памятью, а также системы, в которых каждый элемент взаимодействует не только с ближайшим соседом или несколькими ближайшими соседями, но и со всей системой в целом или ее частями. Типичным примером таких систем являются гравитируюшие системы: звездные скопления, газопылевые комплексы, галактики. Энтропия Цаллиса нашла применение при описании продольных (электростатических) волн в бесстолкновительной плазме, развитой турбулентности, сильно квантово запутанных систем, эволюции сложных сетей, термостатики сильно шунтированного движения взаимодействующих частиц, а также диффузионной кинетики. В системах, чувствительных к начальным условиям производства энтропии идёт на грани хаоса.
Рис. 11. Распределение частиц по энергии в термостатике Цаллиса и эволюция системы с памятью во времени.
Энтропия Цаллиса применена для решения некоторых практически важных задач. При изучении эволюции самогравитирующего газа было обнаружено, что
распределение по скоростям спиральных галактик в скоплениях резко обрывается при 500 км/сек. Аналогичные эффекты предсказывает и термостатистика Цаллиса. Флуктуации магнитного поля в солнечном ветре позволили вычислить q-триплет (или триплет Цаллиса). Продольные (электростатические) волны в бесстолкновительной плазме имеют не максвелловское распределение - спадание при больших скоростях идёт по степенному закону, что позволило обрабатывать результаты по термостатистике Цаллиса. В её рамках было получено распределение скоростей в ведомой диссипативной пылевой плазмы. Термостатистика постепенно находит применение при изучении эволюции сложных

http://profbeckman.narod.ru/
сетей, т.е. систем, состоящих из большого числа узлов, которые могут определенным образом взаимодействовать друг с другом (например, фондовые биржи, компьютерные сети и т.д.). Везде, где важное значение имеет явление "дальнодействия" – каждый узел сети может взаимодействовать не только с несколькими ближайшими соседями, но и со многими удаленными узлами, число которых, к тому же, может меняться со временем. Именно такими случаями и занимается статистика Цаллиса. С помощью этой статистики была интерпретирована релаксация спиновых стёкол. Распределение, характеризующий движение холодных атомов в диссипативных оптических решетках, предсказано в 2003 г., а наблюдалась в 2006 г. Эта статистика нашла применение в обработке результатов, зарегистрированных детекторами на ускорителе ЦЕРНа в экспериментах и изучению столкновений высокоэнергетичных частиц.
Статистика Цаллиса используется для описания процессов, чувствительным к начальным условиям, в которых производство энтропии идёт на грани хаоса, прежде всего это сильно запутанные квантовые системы, термодинамика и сильно шунтированное движение взаимодействующих частиц. Она позволила получить нелинейные обобщения уравнений Шредингера, Клейна-Гордона и Дирака.
Возможно самое перспективное направление использования энтропии Цаллиса – интерпретация явлений аномальной диффузии, в частности – супердиффузия, в рамках которой с использованием пространственно дробных уравнений в частных производных осуществляется непрерывный переход от полного порядка (полуволновое уравнение) к полному беспорядку (диффузионное уравнение). Такой переход можно осуществить изменением параметра q в выражении для энтропии Цаллиса.
