http://profbeckman.narod.ru/

Рис. 12. Бифуркационная диаграмма одномерного отображения примера 8. Сплошная кривая отвечает устойчивым неподвижным точкам отображения, пунктирная – неустойчивым.

При наличии трёх и более параметров в динамических системах нужно строить уже бифуркационные поверхности и гиперповерхности, что значительно усложняет исследование. Можно также фиксировать один из параметров, а другие менять.

15.3 Простейшие бифуркации

Рассмотрим сначала наиболее простые локальные бифуркации регулярных аттракторов, имеющие коразмерность 1. Для анализа таких бифуркаций достаточно рассмотреть семейство систем дифференциальных Ур.1, имеющее одномерное пространство параметров, в котором эти бифуркации являются точечными. Итак, пусть значение μ=0 является бифуркационным значением параметра μ, т. е. именно при этом значении параметра качественно меняется фазовый портрет семейства систем Ур.1.

Пусть системы из семейства (1) при всех значениях параметра μ, лежащих в некоторой окрестности U бифуркационного значения параметра =0, имеют своими решениями либо особые точки (положения равновесия или стационарные точки) x0(μ), либо предельные циклы x0(t, μ), либо инвариантные двумерные торы, устойчивые при всех μ<0. Опишем основные бифуркации, которые могут происходить в этих случаях в семействе систем (1) при переходе параметра через значение μ= 0.

Рассмотрим бифуркации устойчивых особых точек.

Особая (стационарная) точка или положение равновесия однопараметрического семейства систем (1) удовлетворяет условию F(x0(μ),μ)=0. Поэтому, линеаризуя семейство

(1) в окрестности особой точки, получим зависящую от параметра систему обыкновенных дифференциальных уравнений

где y(t)=x(t)-x0(μ). Вектор у=0 является решением системы (14) для всех μ U. Бифуркации, связанные с потерей устойчивости особой точки семейства (1), могут

произойти при переходе параметра через значение, при котором точка является негиперболической. Рассмотрим два основных, наиболее часто встречающихся в приложениях случая: одно собственное значение матрицы А(0) равно нулю или два комплексно сопряженных собственных значения матрицы A(0) лежат на мнимой оси, а все остальные собственные значения имеют отрицательные вещественные части. Бифуркации, приводящие к потере устойчивости особой точки семейства (1), определяются исключительно теми координатами системы (1), которые соответствуют собственным значениям матрицы А(0) лежащим на мнимой оси. Система уравнений, записанная в этих координатах, называется нормальной формой семейства (14) в окрестности особой точки.

Приведём примеры нескольких наиболее распространеных бифуркаций. В первую очередь это бифуркации положений равновесия: "вилка", "обмен устойчивостью", "седлоузел" и "рождение цикла".

1) Касательная бифуркация (бифуркация седло-узел).

Это бифуркация коразмерности 1 – слияние (рождение) пары равновесий. Дано одномерное нелинейное дифференциальное уравнение

http://profbeckman.narod.ru/

Бифуркационные условия

1 x(0)t

где х(0)=х(t=0).

Тогда при t

состоит из двух ветвей, т.е. если Ур.15 имеет положительную правую часть, то у него два решения: x f x0(1) , x f x0(2)

Рис. 13. Фазовое пространство седло-узловой бифуркации: неподвижные точки и потоки для Ур. 20.

Линеаризация Ур.(15) в окрестности стационарного состояния демонстрирует, что неподвижная точка x0(1) – устойчивое состояние (аттрактор), а x0(2) –

неустойчивое состояние (репеллер), для <0 не существует неподвижных точек. При =0 Ур.(16) имеет одну неподвижную точку х0 (шунт – полуустойчивое положение равновесия).

Значение =0 является бифуркационным (изменение поведения системы в этой точке называется седло-узловой бифуркацией)..

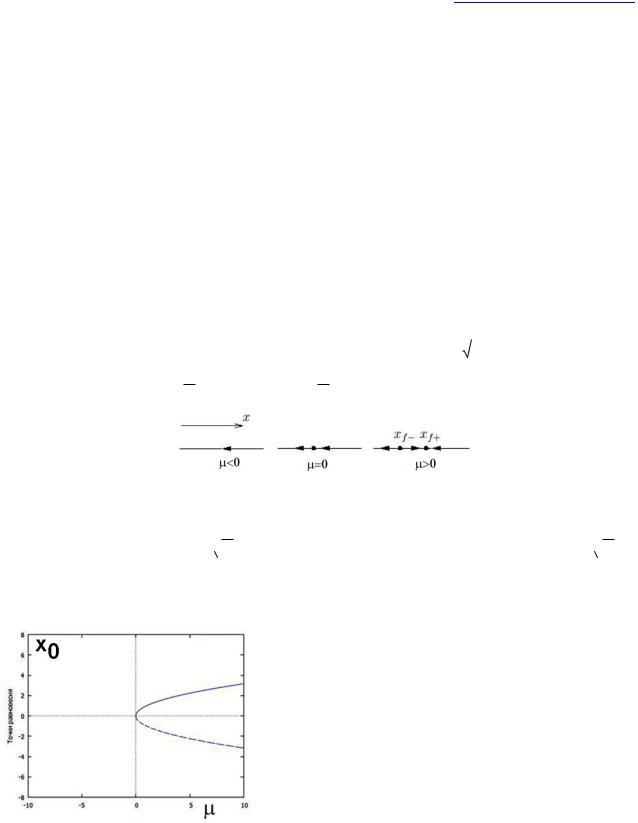
Положения равновесия х0(1;2) определены только для 0; при <0 равновесные состояния отсутствуют.

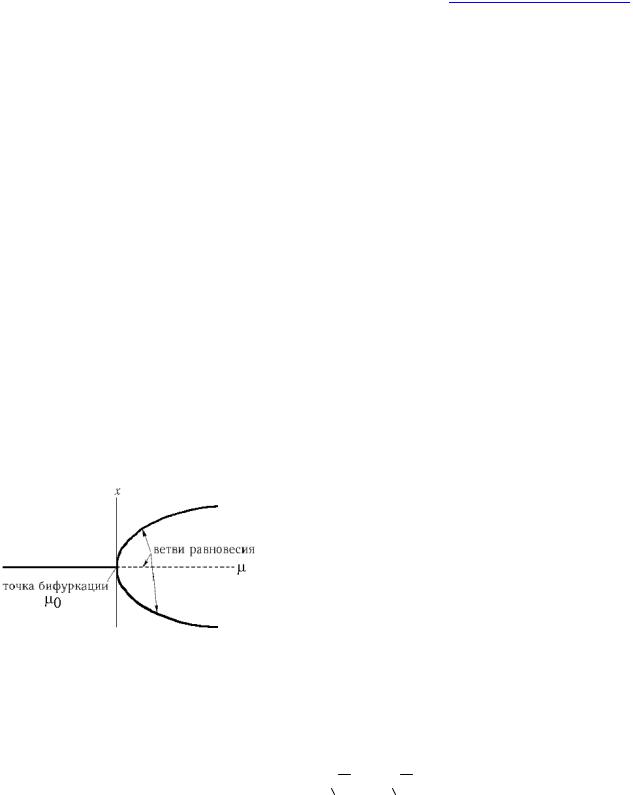
Рис. 14. Фазопараметрическая диаграмма системы (15). Бифуркация пары равновесий: положительные значения и отрицательные точки равновесия касательная (седло-узловая) бифуркация. Cплошная линия показывают устойчивые решения, а пунктирная – неустойчивые.

На рис. 14 изображена соответствующая бифуркационная диаграмма. Как видно из рисунка, из точки бифуркации выходят две ветви равновесных состояний, одна из которых устойчивая, а вторая – неустойчивая. При варьировании параметра в сторону увеличения значений из «ничего» рождаются два состояния равновесия, одно из которых устойчиво. Бифуркации такого рода относят к типу «седло-узел».

Система уравнений для бифуркации седло-узел в более полной форме записывается как

http://profbeckman.narod.ru/

x t x2

Система не имеет положений равновесия, если <0. Система имеет одно положение равновесия P(0; 0), которое является седло-узлом, если =0. Система имеет два

положения равновесия ( ,0), ,0 если >0. Первое является седлом, второе –

устойчивым узлом.

Нормальная форма седло-узловой бифуркации имеет вид y y2.

Рис. 15. Седло-узловая бифуркация на плоскости.

Последнее уравнение при μ<0 имеет два стационарных

решения y12 , одно из которых является асимптотически устойчивым, а другое — нет. При μ

= 0 оба решения сливаются в одно стационарное решение у=0, являющееся асимптотически устойчивым (неустойчивым) для траекторий, начинающихся слева (справа) от нуля. При μ > 0 уравнение не имеет особых точек, и, следовательно, аттрактор исчезает, т.е. рассмотренная бифуркация является кризисом.

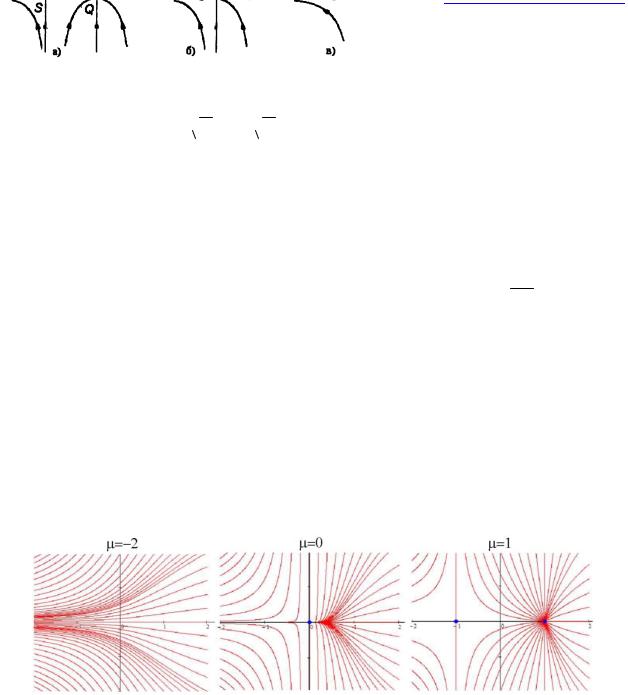
Аналогом этой бифуркации для двумерных систем дифференциальных уравнений является бифуркация, при которой имеющиеся в системе при μ<0 устойчивые узел и седло (рис. 16а) сливаются при μ=0 в вырожденную особую точку – вырожденный седло-узел (рис. 16б), разрушающийся при μ>0 (рис. 16в). В случае размерности пространства больше двух в результате бифуркации устойчивый узел и седло-узел (невырожденный) сливаются при μ=0 в вырожденную особую точку, исчезающую при μ> 0.

Рис. 16. Бифуркация седло-узел.

При обратной седло-узловая бифуркация с нормальной формой 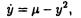происходит одновременное рождение устойчивой и неустойчивой особых точек или устойчивого узла и седла (рис. 15в и 16).

x x2

обязательно узел, а вторая – седло (которые при =0 сливаются в особую точку, называемую седло-узлом.

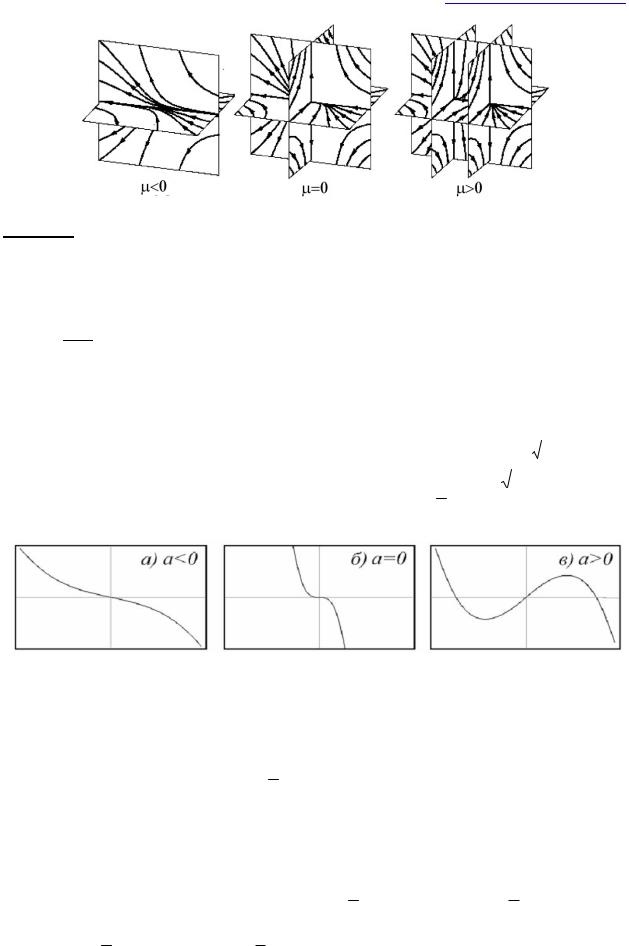
http://profbeckman.narod.ru/

Рис. 17. К примеру 8.

соответствующую потенциальную функцию, и с её помощью дать физическую интерпретацию возможности неподвижных точек, их устойчивости и бифуркаций. Представить уравнения осциллятора в стандартном для динамической системы второго порядка виде, и дать анализ неподвижных точек и их бифуркаций на основе исследования следа и якобиана линеаризованной матрицы. Вводя потенциал U(x), уравнение исследуемого осциллятора можно записать в виде

Соответственно, в системе возможны устойчивая и неустойчивая неподвижные точки. Их легко

потенциальному максимуму и поэтому неустойчива, а точка x0 a соответствует минимуму, и

поэтому устойчива. При a=0 неподвижные точки сливаются (рис.4б) и исчезают (рис.4а).

Рис. 18. Вид потенциальной функции (16) до порога бифуркации (а), в точке бифуркации (б) и за ней (в)

Проведём теперь формальное исследование устойчивости неподвижных точек и их бифуркаций, которое подтвердит наши соображения. Представим уравнение осциллятора в

производные по времени, получаем выражение для нахождения координат неподвижных точек: y=0, y+a-x2=0. Откуда получаем: x0 a . Для анализа устойчивости полученных неподвижных

Теперь находим след и якобиан этой матрицы: S=- и J=-2x0. Анализ типа неподвижной точки можно провести, используя плоскость след-якобиан матрицы М (рис. 19). Тип неподвижной точки будет определятся тем, в какую область этой плоскости попадает точка, заданная координатами S

=−γ и J=-2x0. Для первой неподвижной точки ( x0 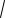a и y =0) имеем J 2a и S=- . Якобиан для этой точки всегда отрицателен, и в соответствии с рис.5, это седло. Для второй неподвижной точки ( x0 a и y=0) имеем J 2a и S =-γ<0. Эта точка является устойчивой. Причем при

http://profbeckman.narod.ru/

J<S2/4 это узел, а при противоположном условии – фокус. В нашем случае точка будет

устойчивым узлом при выполнении условия a 2 . При этом при a=0 этот устойчивый узел

8

сливается с седлом (неустойчивая неподвижная точка), и происходит бифуркаций седло-узел. Её формальным критерием является равенство нулю якобиана матрицы М. Тогда прировняв нулю значение якобиана для неподвижной точки (в данном случае, неважно какой), получим a=0. Это и есть условие седло-узловой бифуркации.

Рис. 19. Различные типы неподвижных точек на плоскости след S - якобиан, J -

матрицы линеаризации. Граница между узами и фокусами дается уравнением J= S2/4.

2) Касательная бифуркация в отображениях (седло-узловая бифуркация; катастрофа складки).

Рассмотрим нелинейное отображение

неустойчива. Будем теперь увеличивать параметр , следя за положением неподвижных точек, а также за их мультипликаторами, которые определяются как 1,2=f'(x0,1,2)/ При увеличении обе неподвижные точки сближаются, вплоть до слияния при =0. В то же самое время соответствующие им мультипликаторы стремятся к 1, одно – справа, а другое

– слева. В момент достижения равенства 1,2=+1,0 обе неподвижные точки сливаются и

бифуркация в отображениях.

Другое название касательной бифуркации – складка. Это становится понятным, если посмотреть на график для неподвижных точек,

который напоминает складку с вершиной в точке =0. Если рассмотреть двупараметрическую систему, то в фазометрическом пространстве этой бифуркации соответствует поверхность, имеющая особенность типа складки вдоль линии l0 на плоскости параметров. Ещё одно название такой бифуркации – седло-узловая пришло из рассмотрения двумерных динамических систем, в связи с тем, что бифуркация соответствует слиянию

устойчивого узла с седлом.

http://profbeckman.narod.ru/

Рис. 21. Бифуркация типа складки.

В касательной бифуркации участвуют две неподвижные точки: устойчивая и неустойчивая. Одновременное достижение их мультипликаторами граничной величины =+1 соответствует их слиянию и исчезновению.

3)Транскритическая бифуркация (бифуркация типа обмен устойчивостью).

Внекоторых моделях неподвижная точка существует при всех значениях параметра, однако может менять тип устойчивости. Изменение типа устойчивости неподвижной точки даёт транскритическая бифуркация. В ней бифуркация седло-узел невозможна.

Вобщем виде система уравнений для бифуркаций обмен устойчивостью

x t x x2

Рис. 22. Векторное поле Ур.(22) при варьировании параметра .

Система имеет:

1) одно положение равновесия P(0; 0), которое является седло-узлом, если = 0;

2) два положения равновесия (0; 0) и ( , 0), если ≠0. Первое является седлом, второе – устойчивым узлом.

Рис. 23. Транскритическая бифуркация (смена

Неподвижная точка х0=0 существует при всех значениях . Для <0 имеется неустойчивая точка х0= и устойчивая х0=0. При =0 неустойчивая точка сливается с устойчивой в начале координат (шунт), равновесная

(негиперболическая) точка х0=0 (седло, при =0 – нестабильная точка). Наконец, при >0 в нуле остаётся неустойчивая точка, а х0= , убегающая от нуля, устойчивая. Если =0, то система подвергается транскритической бифуркации: неподвижные точки меняют тип устойчивости при переходе параметра через значение =0.

Рис. 24. Бифуркация обмен устойчивостью.

Таким образом, два стационарных решения х=0 и х=-μ (у=μ) сосуществуют вместе и обмениваются устойчивостью при переходе параметра через бифуркационное значение μ=0. Бифуркация является мягкой.

http://profbeckman.narod.ru/

Аналогом транскритической бифуркации для двумерных систем дифференциальных уравнений является бифуркация, при которой устойчивый узел становится седлом, а седло становится устойчивым узлом. В случае размерности пространства больше двух в результате рассмотренной бифуркации устойчивый узел или устойчивый фокус становятся седло-узлом или седло-фокусом, а седло-узел или седлофокус – устойчивыми узлом или фокусом. Принципиальная разница между транскритической бифуркацией и бифуркацией «седло-узел» заключается в том, что в транскритическом случае неподвижные точки не исчезают после бифуркации, они лишь «меняются устойчивостями».

4) Транскритическая бифуркация в отображениях

Рассмотрим отображение

и затем удаляется. При этом в точке =0 неподвижные точки обмениваются устойчивостью: если при 0 точка х20 – устойчива, а х10 – нет, то при 0 - наоборот!

Именно эта характерная особенность и определила название бифуркации.

График для собственных значений неподвижных точек можно построить из (24), вычислив производную и подставив туда значения неподвижных точек.

Получаем: f'(xn)=1-+2x, x10=0: 1=1-, х20= : 2=1+ .

Рис. . Обе прямые пересекаются в точке транскритической бифуркации = 0 и 1,2 = + 1.

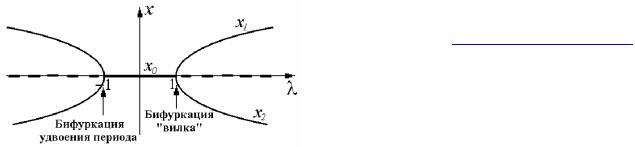
5) Бифуркация типа вилки (бифуркация потери симметрии).

Бифуркация типа вилка - особый тип локальной бифуркации, где система переходит из одной неподвижной точки в три неподвижные точки.

Рис. 14. Бифуркационная диаграмма: бифуркация типа вил, отвечающая переходу из состояния с одним устойчивым положением равновесия в состояние с двумя устойчивыми равновесными точками: сплошные линии - устойчивое состояние (стоки), пунктир – неустойчивое состояние (источники).

Система уравнений для бифуркации типа вилка имеет вид*x t x x3

Система имеет:

1)одно положение равновесия P(0; 0), которое является устойчивым узлом, если α

0; (0;0),

2) три положения равновесия (0;0), ,0 , ,0 , если >0. Первое является седлом, два других – устойчивыми узлами.

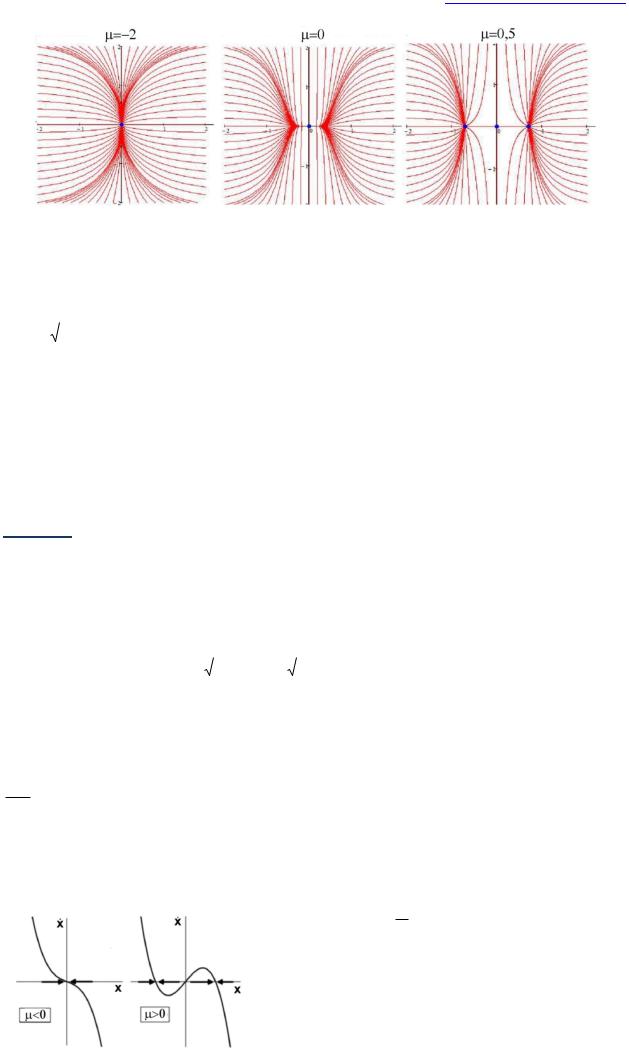
http://profbeckman.narod.ru/

Рис. 15. Бифуркация типа «вилка»

Существуют два вида этой бифуркации: надкритическая и подкритическая, имеющие нормальные формы

стационарное решение, становясь неустойчивым, порождает два других устойчивых стационарных решения. Бифуркация также является мягкой.

Сверкритический случай. Нормальная форма бифуркации надкритической вилы

dt

где – внешний управляющий параметр.

Ур.27 предложено Ландау (1944) для описания влияния нелинейностей на линейную гидродинамическую неустойчивость, причем амплитуда возмущения определялась х.

Замечание. Ур.27 – каноническая форма бифуркации вил. Бифуркация бифуркаций является общей для задач, имеющих симметрию (Ур.27) инвариантно относительно замены переменных х→-х).

Это уравнение инвариантно относительно замены x на −x.

В зависимости от значения возможны три различных варианта векторного поля. Неподвижные точки определяются как решения алгебраического уравнения

Если 0 существует только одна ветвь, а если >0, то три ветви, которые пересекаются в точке бифуркации при =0 и х=0. Критическая точка х1 стабильна при <0, и нестабильна, если >0, тогда как х2,3 стабильны при >0 и нестабильны при <0. Эти две имеют противоположные стабильности и меняют свои стабильности при переходе через точку бифуркации при =0. Заметим, что в точке бифуркации х=0, но всё ещё

d

0. Для отрицательных значений , <0, существует одно устойчивое равновесие

dx0

при х=0 (начало координат – единственная неподвижная точка и она устойчивая). Если =0 начало всё ещё устойчиво, но эта устойчивость слабая, т.к. линейный член исчезает (и производная F'(0)=0). Здесь решения стремятся к тривиальному очень медленно. Наконец, когда >0, начало координат становится неустойчивым. Два стабильных равновесия (неподвижные точки) возникают по обе стороны от

нуля при х0(2;3) . (рис.15).

http://profbeckman.narod.ru/

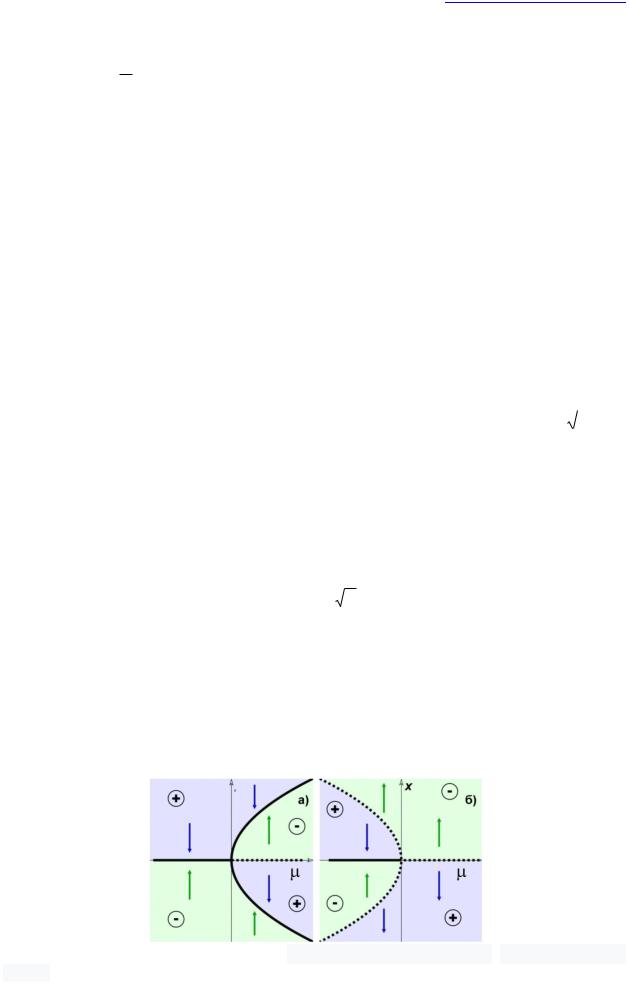
Аналогом этой бифуркации для двумерных систем дифференциальных уравнений является бифуркация, при которой устойчивый узел становится седлом, в окрестности которого симметрично рождаются два новых устойчивых узла (рис. 18). В случае размерности пространства больше двух в результате рассмотренной бифуркации устойчивый узел становится седло-узлом, а родившиеся в его окрестности устойчивые особые точки могут быть не только узлами, но и фокусами, т.е. иметь наряду с одним отрицательным вещественным собственным значением матрицы линеаризации ещё два комплексно сопряженных собственных значения с отрицательными вещественными частями.

Рис. 18. Бифуркация типа вилки

при переходе параметра r через значение r=1 и во многих других нелинейных системах дифференциальных уравнений, включая консервативные системы. В последнем случае эллиптическая особая точка становится седловой, порождая две другие эллиптические особые точки. В случае подкритической бифуркации стационарные решения имеют вид: у

=0 и y12 (последние два решения определены только при μ<0). Таким образом,

устойчивое стационарное решение (узел) становится неустойчивым (седлом, седло-узлом, седлофокусом), а вместе с этим исчезают два других неустойчивых стационарных решения (седла, седло-узла, седло-фокуса). Бифуркация является кризисом.

точки: x0;2,3 . Собственные значения неподвижных точек есть: 1=1+ , 2,3=1-2 .

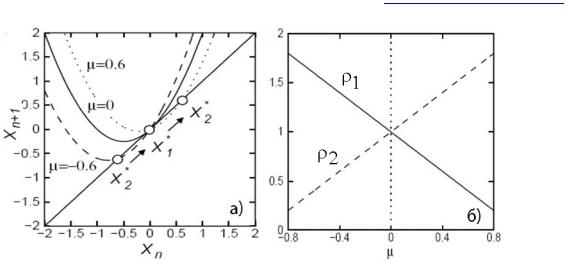
Если -2< <0, то x10 – устойчива. Если =0, то от нее «отщепляются» устойчивые x20 и x30, сама же x10 теряет устойчивость. 1,2,3=+1 при = 0.

Изобразим графически изменение собственных значений в неподвижных точках в зависимости от :

Прямые пересекаются в точке транскритической бифуркации =0 и 1,2=+1.

http://profbeckman.narod.ru/

Рис. 19. Бифуркация типа вилы в отображении. Эволюция системы при транскритической бифуркации. Изменение собственных значений в неподвижных точках в зависимости от .

Бифуркационная диаграмма для отображения (32) напоминает вилы, откуда и следует название рассматриваемой бифуркации. Данный вариант вилообразной бифуркации является суперкритическим, т.к. новые неподвижные точки рождаются в момент бифуркации и существуют далее.

Существует другой вариант этой бифуркации. Замена знака перед кубическим членом в отображении (32) дает новое отображение

xn+1=(1+ )xn+xn3. (33)

Оно имеет три неподвижные точки при <0 и одну x10=0 при >0. При <0 x10=0 является устойчивой, а две точки x20 и x30 – неустойчивые. При =0 точка x10 также претерпевает бифуркацию и теряет устойчивость. Однако общая картина эволюции состояний равновесия иная. При увеличении два неустойчивых состояния равновесия «влипают» в устойчивую точку x10 и исчезают, а сама x10 теряет устойчивость. Данный вариант – субкритическая бифуркация, т.к. к моменту бифуркации пара неустойчивых неподвижных точек исчезает.