Добавил:

Tamaki_Syo Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебники / НЕЛИНЕЙНАЯ ДИНАМИКА СЛОЖНЫХ.pdf

Скачиваний:

893

Добавлен:

30.03.2022

Размер:

28.89 Mб

Скачать

☆

<<< < Предыдущая 46 47 48 49 50 51 52 53 54 55 56 5758 / 8758 59 60 61 62 63 64 65 66 67 68 69 70 > Следующая >>>

http://profbeckman.narod.ru/

минимизаторы энергетической функции должны быть устойчивыми (но не обязательно асимптотически устойчивыми) равновесиями.

Простейшим фазовым портретом является неподвижная точка на прямой.

В понятии устойчивость по Ляпунову реализуется идея малых отклонений решения дифференциального уравнения на промежутке времени [0,+ ] при небольших вариациях начальных данных этого решения.

x x y

Пример 16. Система

имеет критические точки (1,1)

и (-1;-1). Якобиан

y x

При

(1;1) линеаризованная система

имеет матрицу

коэффициентов

2у

Собственное

значение

. Критическая точка

- нестабильное

2х

седло.

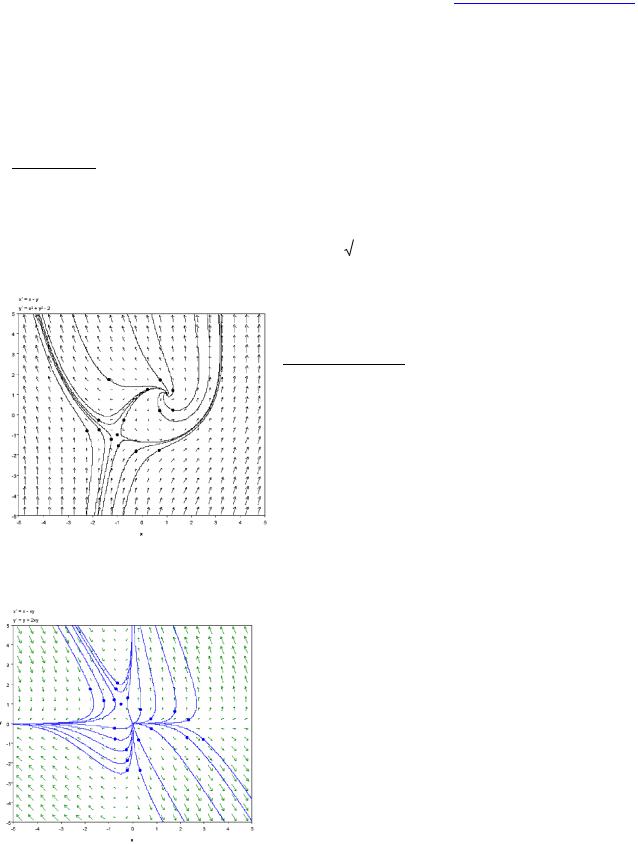
Рис. 23. К примеру 16: (1;1) - нестабильный

фокус; (-1,-1) нестабильное седло.

Пример

17.

Критические

точки

системы

(0;0)

и (-0,5;1) Якобиан

1 y

x x xy

2 y

1 2x

y y 2xy

При

(0;0)

матрица

коэффициентов

линеаризованной системы А

Она имеет

повторяющееся собственное значение r=1. У линейной системы нет нестабильного истинного узла (звезды). Но как нелинейная система имеет нестабильный узел. При (-1/2;1) линеаризованная

0 1/ 2

система имеет матрицу коэффициентов А . Собственное значение r=1 и -1.2 0

Критическая точка – нестабильное седло.

Рис. 24. К примеру 17: (0;0) – нестабильный узел; (- 1/2;1) – нестабильное седло.

14.10 Устойчивость решений дискретных уравнений

В дискретных динамических системах могут существовать частные решения, представляющие собой стационарные, периодические, квазипериодические и хаотические последовательности, которые мы будем обозначать xn*. Рассмотрим первое частное решение дискретной системы – стационарное, или решение в виде

неподвижной точки.

Точка x* называется неподвижной точкой отображения F(х*), если выполняется

условие:	(26)
x* = F(x*).

Это условие означает, что при графической итерации отображения движение при попадании в x* прекращается. Итерации вновь и вновь помещают очередное xn в x*.

http://profbeckman.narod.ru/

Решение в виде неподвижной точки еще называется состоянием покоя или состоянием равновесия. Помимо самого факта существования в дискретных системах решений в виде неподвижных точек (состояний покоя или равновесия системы), важную роль играет информация об их устойчивости или неустойчивости. Устойчивость какоголибо состояния (движения) динамической системы определяется просто: введём небольшое отклонение (возмущение) динамической системы от исследуемого состояния и проанализируем, каким будет её дальнейшее поведение. Если со временем система вернется в исходное состояние (возмущение затухает), то такое состояние называется устойчивым. Если начальное отклонение нарастает со временем – состояние неустойчиво.

Найдем условия устойчивости неподвижной точки x*. В связи с тем, что проблема устойчивости связана с анализом реакции системы на малое возмущение ее состояния, на первом этапе она может быть исследована в рамках линейного приближения.

Пусть x = x* + , – отклонение от состояния равновесия, малая по сравнению с x* величина. Тогда отображение примет вид:

x*+n+1=F(x*+n). (27)

Применяя для правой части (27) разложение в степенной ряд в окрестности неподвижной точки и отбрасывая члены порядка малости выше первого, находим:

x*	n 1	F(x* )	F		n	.	(28)
x*		F(x* )	x			.	(28)

				x*
				x*

Производные берутся в точках частного решения, в данном случае в неподвижной точке x*. Тогда

n 1	F	n .	(29)
	x
		x*

Введём обозначение aik		fi			. Здесь	индексы i,k = 1,…, N – размерность
Введём обозначение aik		xk			. Здесь	индексы i,k = 1,…, N – размерность
		xk		x	*
				x
отображения. Тогда Ур. 29 можно переписать в координатной форме:
N
ni 1 aik nk .						(30)
k 1
Данное линейное точечное отображение есть линейное дискретное уравнение в
вариациях. В матричной форме (30) можно записать в следующем виде:
n 1 A n .						(31)
Матрица А с элементами	aik		является			квадратичной и называется матрицей

линеаризации или матрицей Якоби. Устойчивость неподвижной точки отображения определяется мультипликаторами k , которые являются собственными значениями матрицы А, или корнями характеристического уравнения:

det A E 0.

(32)

E – единичная матрица. Неподвижная точка x* исходного отображения (4) является устойчивой, если все мультипликаторыk удовлетворяют условию | k| < 1. Если среди мультипликаторов имеются такие, для которых | k| > 1, то неподвижная точка отображения (4) будет неустойчивой.

Рис. 25. Линеаризация в особой точке.

Прежде всего, рассмотрим устойчивость неподвижных

точек одномерного отображения
Одномерное отображение:
xn 1 f (xn ).	(33)

http://profbeckman.narod.ru/

Пусть x* – неподвижная точка отображения. Введем малое возмущение : Тогда отображение (33) примет вид:

xn 1

x* n 1

f (xn ) f (x* n ).

(34)

Используя выражения (28), (29), приходим к новому одномерному линейному отображению, описывающему эволюцию малого возмущения неподвижной точки, которое имеет вид:

n 1

f (x* ) n .

(35)

Собственное значение матрицы линеаризации A или мультипликатор неподвижной точки одномерного отображения есть =f(x*). Следовательно, условие устойчивости неподвижной точки x* сводится к выполнению неравенства |f(x*)|<1. Если |f(x*)|>1, неподвижная точка неустойчива. Поведение неподвижной точки зависит от величины и знака производной f (x*). С геометрической точки зрения значения f(x*) – это тангенс

угла наклона графика функции f(х) в точке x*. Эволюции малого возмущения n соответствует сжатие либо растяжение отрезка, соответствующее отклонению от x*. В малой окрестности неподвижной точки нелинейную функцию можно заменить прямой А, касательной к f(x) в точке x*.

Рис. 26. Типы неподвижных точек в одномерном отображении.

1) f'(x*)>1: отклонение n растёт по модулю, не меняя своего знака, неподвижная точка неустойчива;

2)0<f'(x*)<1: отклонение n монотонно убывает, неподвижная точка х* устойчива.

3)f'(x*)<-1: отклонение n нарастает по модулю, меняя знак при каждой итерации, неподвижная точка х* неустойчива;

4)-1<f'(x*)<0: отклонение n убывает по модулю, меняя свой знак при каждой итерации, неподвижная точка х* устойчива;

5)f'(x*)=1: отклонение n не меняется, исходное состояние х* нейтрально по отношению к возмущению ;

6)f'(x*)=-1: n меняет знак на каждом шаге интегрирования, не нарастая и не убывая по модулю, х* нейтрально.

Переходные значения параметра называются критическими. Им соответствуют

точки бифуркации 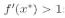. Если возмущение меняет знак при каждой итерации, то к названию неподвижных точек добавляют слово «обратный».

Рассмотрим теперь устойчивость неподвижных точек двумерного отображения.

x	n 1	f (x	, y	n	),		x* f (x, y),
		n				Неподвижная точка (х,у) задаётся условием		Введём малые
		g(xn , yn ).
yn 1							y* g(x, y).

x * n ,

xn 1 x * n 1 f x * n , y * n

отклонения и :

Тогда

y * n.

yn 1 y * n 1 g x * n, y * n

Разложение в ряд Тейлора:

n 1

2 f

y 2

...

x n

y n

n n

, где нижние индексы у

f и

g означают

...

n 1

x n

y n

n n

производные, взятые в неподвижной точке (х*,у*). Для достаточно малых и можно

http://profbeckman.narod.ru/

ограничиться линейной частью этого уравнения. Тогда, обозначая a=fx, b=fy, c=gx, d=g

или в матричной форме

n 1

получим уравнения в вариациях

n 1

Чтобы найти мультипликаторы неподвижных точек отображения или собственные

значения

матрицы

линеаризации,

необходимо найти корни

характеристического

уравнения. Для двумерного отображения оно имеет вид: det

Характеристическое уравнение

2 (a d) (ad bc) 0.

Его корни

(a d)

(a d)2

(ad bc)

1,2

(36)

определяют

поведение фазовых траекторий в окрестности неподвижной точки

отображения.

Перейдём теперь к анализу неподвижных точек в

двумерном отображении.

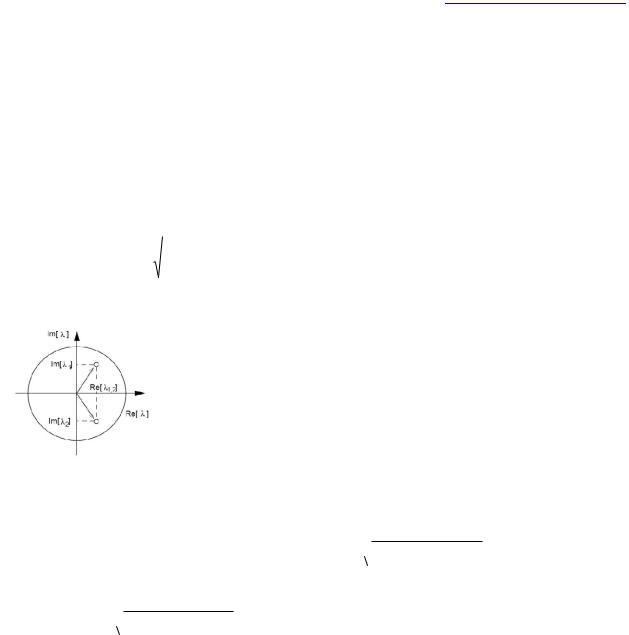
Рис. 27. Корни характеристического уравнения на комплексной плоскости.

Из Ур.36 следует, что собственные значения 1,2 могут быть действительными числами или комплексно сопряженными. Характер устойчивости неподвижной точки меняется при | 1,2|=1. Поэтому удобно характеризовать неподвижную точку,

изображая расположение собственных чисел 1 и 2 на комплексной плоскости относительно единичной окружности. Пара комплексно сопряженных значений | 1,2|<1, имеющие равные действительные части, а их мнимые части различаются только знаком.

Положение точек внутри окружности означает, что Re2 1,2 Im2 1,2 1.

Случай комплексно сопряженных 1 и 2.

В данном случае неподвижная точка является фокусом.

Если r Re2 1,2 Im2 1,2 1, то неподвижная точка называется устойчивым

фокусом. В этом случае точки итерации исходного отображения лежат на скручивающейся спирали с центром в неподвижной точке, которая в этом случае устойчива. Если r>1, то спираль раскручивается, удаляясь от неустойчивой неподвижной точки, которая в данном случае является неустойчивым фокусом. Характер сходимости возмущенной траектории к неподвижной точке меняется в зависимости от знака Re 1,2. Случай r=1 соответствует пограничной ситуации, когда возмущенная траектория не удаляется и не приближается к неподвижной точке, вращаясь вокруг нее с некоторой угловой скоростью.

Случай действительных 1 и 2.

http://profbeckman.narod.ru/

Рис. 28. Особые точки отображений.

Рис. 29. Фокусы в случае комплексно сопряженных корней.

<<< < Предыдущая 46 47 48 49 50 51 52 53 54 55 56 5758 / 8758 59 60 61 62 63 64 65 66 67 68 69 70 > Следующая >>>

Соседние файлы в папке Учебники

#
30.03.20221.94 Mб59[Ageev_E.P.]_Neravnovesnaya_termodinamika_v_vopros(BookSee.org).pdf
#
30.03.20224.11 Mб71Лекции по термодинамике неравновесных систем. Пармон.pdf
#
30.03.202228.89 Mб893НЕЛИНЕЙНАЯ ДИНАМИКА СЛОЖНЫХ.pdf
#
30.03.20221.21 Mб46Равновес и неравновес термодинамика.pdf
#
30.03.20223.97 Mб63Физика конденсированных сред.pdf