
- •Аннотация
- •От автора
- •ПРЕДИСЛОВИЕ
- •ВВЕДЕНИЕ
- •1. СИСТЕМЫ И ПРОЦЕССЫ
- •2. ПОРЯДОК, НЕПОРЯДОК, БЕСПОРЯДОК И ХАОС
- •3. ТЕРМОДИНАМИКА
- •3.1 Начала термодинамики
- •3.2 Равновесная термодинамика
- •4. НЕРАВНОВЕСНАЯ ТЕРМОДИНАМИКА
- •4.1 Диссипативные структуры, системы и среды
- •4.2 Термодинамика необратимых процессов
- •4.3 Линейная неравновесная термодинамика
- •4.4 Нелинейная неравновесная термодинамика
- •4.5 Статистическая термодинамика
- •5. ЭНТРОПИЯ
- •5.1 Определение и свойства энтропии
- •5.2 Энтропия в химической термодинамике
- •5.3 Энтропия в статистической физике
- •5.3.1 Энтропия Больцмана-Планка
- •5.3.2 Энтропия Гиббса
- •5.4 Тсаллис (Цаллис) энтропия (Революция в термодинамике)
- •6. ГЕОМЕТРИЯ ФРАКТАЛОВ
- •6.1 Элементы геометрии фракталов
- •6.2 Размерности фракталов
- •6.3 Примеры фракталов
- •6.4 Фракталы и энтропия
- •7. ИНФОРМАТИКА
- •7.1 Информация, информатика и информационные технологии
- •7.2 Теория информации
- •7.2.1 Информация Хартли
- •7.2.2 Энтропия Шеннона
- •7.3 Отрицательная энтропия, антиэнтропия, экстропия
- •7.4 Алгоритмическая теория информации
- •7.4.1 Энтропия Колмогорова
- •7.4.2 Эпсилон-энтропия
- •7.5 Энтропия Кульбака-Лернера
- •7.6 Энтропия Реньи
- •7.7 Квантовая информатика
- •7.7.1 Некоторые положения квантовой механики
- •7.7.2 Энтропия фон Неймана
- •7.7.3 Линейная энтропия
- •7.7.4 Сравнение энтропий Реньи, Цаллиса и Неймана
- •7.7.5 Энтропия Холево
- •8. СИНЕРГЕТИКА
- •8.1 Синергизм и синергетика
- •8.2 Детерминизм, случайность и неопределённость
- •8.3 Простые и сложные системы
- •8.4 Анализ систем
- •8.5 Параметры порядка (управляющие параметры)
- •8.6 Процессы самоорганизации
- •9. СИСТЕМЫ И ЗАКОНЫ ИХ ЭВОЛЮЦИИ
- •9.1 Статические системы
- •9.2 Динамические системы
- •9.3 Линейные динамические системы
- •9.4 Нелинейные динамические системы
- •9.5 Эволюция динамической системы
- •9.6 Математическое описание эволюции динамической системы
- •10. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ОПИСАНИИ ДИНАМИЧЕСКИХ СИСТЕМ
- •10.1 Обыкновенные дифференциальные уравнения
- •10.2 Фазовое пространство и пространство состояний
- •10.3 Линейные ОДУ на плоскости
- •10.4 Нелинейные дифференциальные уравнения
- •11. ОТОБРАЖЕНИЯ
- •11.1 Системы с дискретным временем в отображениях
- •11.2 Итерации в исследовании динамических систем
- •11.3 Графические методы нахождения неподвижных точек и исследования их свойств
- •11.4 Многопараметрические отображения
- •11.5 Примеры некоторых важные отображений
- •12. ОСОБЫЕ ТОЧКИ ФАЗОВЫХ ПОРТРЕТОВ ДИНАМИЧЕСКИХ СИСТЕМ
- •12.1 Дифференциальные уравнения и особые точки
- •12.2 Классификация точек равновесия
- •12.3 Фазовые портреты и особые точки нелинейных ОДУ
- •12.4 Многомерные системы
- •13. РЕГУЛЯРНЫЕ АТТРАКТОРЫ И РЕПЕЛЛЕРЫ
- •13.1 Типы аттракторов
- •13.2 Фазовый объём
- •13.3 Репеллеры
- •13.4 Осциллятор и осцилляции
- •14. УСТОЙЧИВОСТЬ ДИНАМИЧЕСКИХ СИСТЕМ
- •14.1 Устойчивые и неустойчивые равновесия
- •14.2 Устойчивость по Ляпунову (метод первого приближения)
- •14.3 Показатель Ляпунова
- •14.4 Устойчивость нелинейной системы
- •14.5 Метод функций Ляпунова
- •14.6 Функция Ляпунова и энтропия
- •14.7 Асимптотическая устойчивость
- •14.8 Устойчивость особых точек
- •14.9 Устойчивость особых точек
- •14.10 Устойчивость решений дискретных уравнений
- •15. БИФУРКАЦИИ
- •15.1 Бифуркации: основные понятия и классификация
- •15.2 Элементы теории бифуркаций
- •15.3 Простейшие бифуркации
- •16. БИФУРКАЦИИ ЦИКЛОВ
- •16.1 Предельные циклы
- •16.2 Устойчивость предельных циклов
- •16.3 Бифуркации устойчивых предельных циклов
- •16.5 Бифуркация рождения пары устойчивых замкнутых траекторий.
- •16.6 Транскритическая (обмена устойчивостью между циклами) бифуркация.
- •16.7 Бифуркация исчезновения (рождения) пары замкнутых траекторий.
- •16.8 Бифуркация удвоения периода цикла
- •16.9 Бифуркация рождения (гибели) двумерного тора.
- •16.10 Гомоклиническая бифуркация рождения/исчезновения цикла
- •17. ДИНАМИЧЕСКИЙ ХАОС
- •17.1 Хаос статистический и динамический
- •17.2 Предсказание статического поведения системы
- •17.3 Сценарии перехода к хаосу
- •17.4 Примеры систем с хаосом
- •18. ХАОС В ЛИНЕЙНЫХ ОДНОМЕРНЫХ СИСТЕМАХ
- •18.1 Бифуркационные диаграммы
- •18.2 Лестница Ламерея
- •18.3 Отображение Бернулли
- •18.4 Треугольное отображение
- •18.5 Отображение «тент»
- •18.6 Канторов репеллер
- •18.7 Детерминированная диффузия
- •19. ХАОС В ЛОГИСТИЧЕСКОМ ОТОБРАЖЕНИИ
- •19.1 Переход к хаосу через удвоение периода
- •19.2 Логистическое уравнение
- •19.3 Дискретное логистическое уравнение
- •19.4 Логистическое отображение
- •19.5 Бифуркационная диаграмма логистического отображения
- •19.6 Цикл периода 3
- •19.7 Фазовые диаграммы логистического отображения
- •19.8 Аттракторы и фракталы в логистическом отображении
- •20. ХАОС В НЕЛИНЕЙНЫХ ОДНОМЕРНЫХ ОТОБРАЖЕНИЯХ
- •20.1 Отображение xn+1=С+xn2.
- •20.2 Отображение xn+1=а-xn2.
- •20.3 Подобие окон периодической динамики
- •20.4 Порядок Шарковского
- •20.5 Универсальность Фейгенбаума
- •20.6 Устойчивость циклов одномерных отображений
- •20.7 Топологическая энтропия
- •20.8 Синус-отображение
- •21. ХАОС В НЕЛИНЕЙНЫХ ДВУМЕРНЫХ ОТОБРАЖЕНИЯХ
- •21.1 Отображение Эно (Henon map)
- •21.2 Отображение подковы и отображение пекаря
- •21.3 Отображение «кот Арнольда» (Arnold’s cat map)
- •22. НЕРЕГУЛЯРНЫЕ АТТРАКТОРЫ
- •22.1 Хаос в консервативных и диссипативных системах
- •22.2 Регулярные и хаотические аттракторы
- •22.3 Квазиаттракторы
- •22.4 Хаотически аттракторы
- •22.5 Негиперболические хаотические аттракторы
- •22.6 Фрактальные аттракторы
- •22.7 Характеристика нерегулярных аттракторов
- •22.8 Странные нехаотические аттракторы
- •22.9 Сингулярные аттракторы
- •22.10 Многомерные нерегулярные аттракторы
- •22.11 Дикие аттракторы
http://profbeckman.narod.ru/
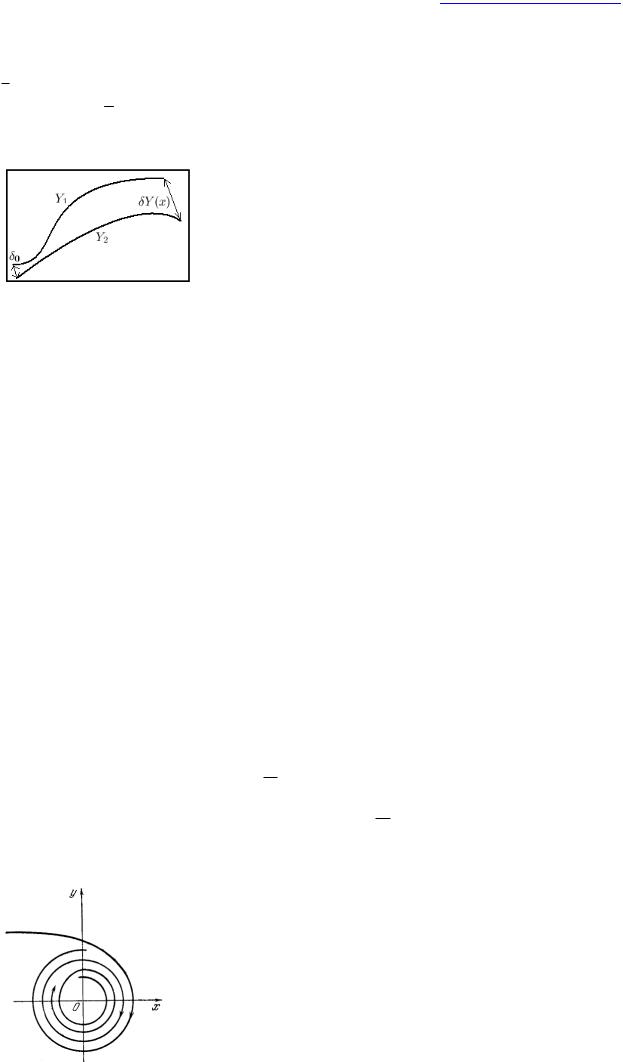
Здесь Sравн – значение энтропии в состоянии равновесия; S и 2S – первая и вторая вариации энтропии системы. Под вариацией какого-либо параметра Y понимают отклонение величины этого параметра от его стационарного или равновесного значения Y под воздействием внешних возмущений:
Y Y Y |
(22) |
Поскольку Sравн – максимальное значение энтропии, член первого порядка S обращается в нуль, и следовательно, устойчивость состояния системы, находящейся вблизи равновесия, определяется знаком члена второго порядка 2S. Таким образом, в области, близкой к
равновесию, 2S играет роль функции Ляпунова.
Рис. 14. Расходимость фазовых траекторий.
Вторая вариация энтропии нелинейной системы (например, многофазной гетерогенной среды), в
окрестности состояния равновесия отрицательна: 2S<0.
Для справедливости этого неравенства требуется выполнение следующих условий: условие тепловой устойчивости в фазах; условие механической устойчивости; условие устойчивости по отношению к диффузии в фазах; условие устойчивости равновесия при фазовом переходе. Все эти условия важны. Так, если бы нарушилось условие тепловой устойчивости, то закон Фурье приводил бы не к затуханию, а к усилению небольших флуктуаций температуры в фазах. Диффузионное условие означает, что при небольших флуктуациях по концентрациям система стремится восстановить однородность в фазах (т.е., действует закон Фика). Если система устойчива по отношению к диффузии, то все химические равновесия (для случая, когда в системе протекают химические реакции) также устойчивы. Условие устойчивости равновесия при фазовом превращении является следствием условия стабильности по отношению к диффузии. При выполнении этих условий вторая вариация энтропии системы является отрицательно определённой квадратичной формой. Следовательно, эти условия – необходимые и достаточные условия устойчивости равновесия и стационарных состояний системы вблизи равновесия. Но как только система удаляется от равновесия, эти условия перестают быть достаточными для устойчивости стационарных состояний системы.
Вторая вариация энтропии термодинамической системы – функция Ляпунова для стационарных состояний системы вдали от равновесия, т.к. в стационарном состоянии она
равна нулю Y 0 , а в его окрестности – отрицательно определённая квадратичная форма. Следовательно, для устойчивости стационарного состояния вдали от равновесия необходимо, чтобы производная термодинамической функции Ляпунова 2S имела положительный знак в окрестности этого состояния. В случае совпадения знаков термодинамической функции Ляпунова и её производной исходное стационарное состояние системы становится неустойчивым, и возможно возникновение качественно
иного состояния системы. Если 2S 0 то стационарное состояние системы,t
находящейся вдали от равновесия, устойчиво, а если 2S 0 – неустойчиво. Анализ
t
устойчивости систем, осуществляемый с помощью производной термодинамической функции Ляпунова, называется термодинамическим анализом.
14.7 Асимптотическая устойчивость
Анализ асимптотической устойчивости имеет свои особенности, особенно, если речь идет о предельных циклах.

http://profbeckman.narod.ru/
Как уже упоминалось, траектории могут обладать некоторыми предельными свойствами.
Рис. 15. Устойчивость предельного цикла.
Точка q фазового пространства называется -предельной точкой точки р, если
существует последовательность моментов времени {tn}, tn |
при n такая, что |
|
q lim f ( p,tn ). Если же tn, то точка |
q lim f ( p,tn ). называется -предельной точкой |
|
n |
n |
|
точки р. Так, например, асимптотически устойчивое положение равновесия является - предельной точкой для всех точек, лежащих в достаточно малой окрестности этого положения. Точки предельного цикла, на который навиваются спиралевидные кривые (рис.2), так же являются -предельными для точек, принадлежащих этим кривым. В обоих примерах -предельные точки составляют целые траектории (в первом случае - особая точка, во втором - предельный цикл).
Теорема. Множество -предельных ( -предельных) точек данной точки есть замкнутое множество, состоящее из целых траекторий.
Можно доказать, что предельная точка для предельных точек множества снова является предельной точкой этого множества. Допустим, что точка q является - предельной точкой для точки р, и покажем, что точка f(q, ) (число может иметь как положительный, так и отрицательный знак) также является -предельной для точки р. В самом деле, если q lim f ( p, tn ) , то из группового свойства динамических систем и
n
свойства непрерывности f(p,t) как функции р, получим f (q, ) lim f ( p,tn ) , а это и
n
означает, что точка f(q,p) является -предельной точкой точки р, т.е. все точки траектории, выходящей из q, являются -предельными точками для р.
Множество, состоящее из целых траекторий, называется инвариантным множеством. Инвариантное множество А обладает тем свойством, что f(A,t)=A при любом t. Если же f(A,t) A при t>0, то множество А называется положительным инвариантом.
Замечание. Если траектория f(p,t) не выходит при t>t0 из ограниченной части пространства, то множество её -предельных точек не пусто.
Если существует функция Ляпунома V, ограниченная снизу (сверху) в положительной инвариантной области D, и если производная во времени V этой функции знакоотрицательна (знакоположительна) в этой области, то все -предельные точки р лежат на одной и той же поверхности уровня функции V.
Теорема. Если существует определённо положительная функция V такая, что V 0 вне М и V 0 на М, где М – множество, не содержащее целых траекторий, кроме точки О, то положение равновесия О асимптотически устойчиво.
Эта теорема позволяет решить вопрос об асимптотической устойчивости с помощью функции Ляпунова, имеющей знакопостоянную производную. В конкретных примерах именно такие функции Ляпунова удается построить для нелинейных систем.
14.8 Устойчивость особых точек
Рассмотрение проблемы устойчивости динамической системы обычно сводят к задаче исследования устойчивости особой точки. Устойчивость особой точки, определяется тем, уйдет или нет изображающая точка при малом отклонении от стационарного состояния.
Как уже упоминалось, устойчивость неподвижных точек двумерной:
|
dx |
ax by, |
dy |
cx dy |
|
|
|
|
(23) |
||
|
dt |
dt |
|||
определяется корнями характеристического уравнения: |
|
||||
2-(a+d)+(ad-bc)=0 |
(24) |
||||
|
|
|
|
|
|
http://profbeckman.narod.ru/ |
Его решение этого: |
|
|
||||
|
|
|
|
|
|
|
|
|
a d |
|
a d 2 |
4 ad bc |
(25) |
|
|
|
||||
1,2 |
2 |
|
|
4 |
|
|
|
|
|
|
|||
Если подкоренное выражение отрицательно, то 1,2 комплексно сопряженные числа. Предположим, что оба корня Ур.26 имеют отличные от нуля действительные части и что нет кратных корней.
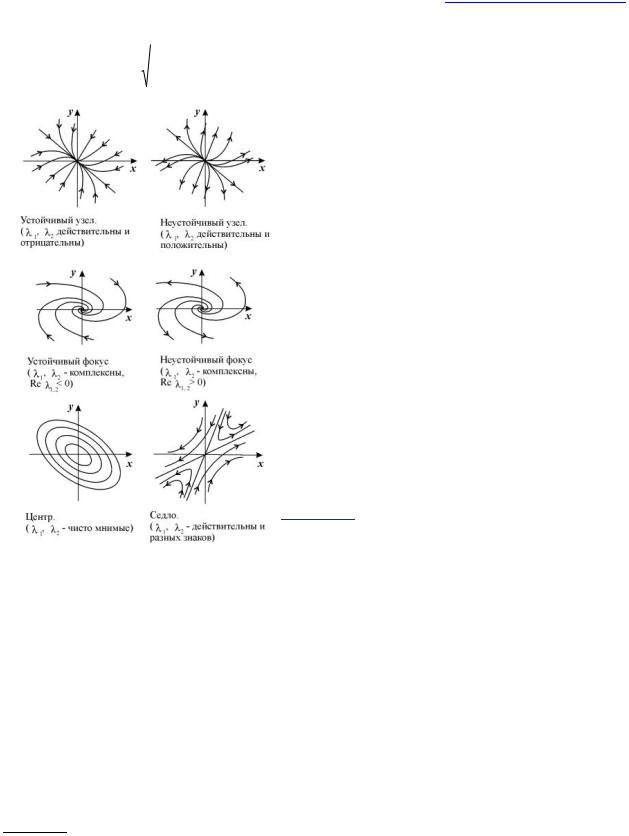
В данном случае возможны шесть типов состояния равновесия в зависимости от характера корней характеристического Ур.26. Вид фазовых траекторий на плоскости x, y для этих шести случаев изображен на рис. 16.
Рис. 16. Типы фазовых портретов в окрестности стационарного состояния для системы линейных уравнений.
Пять типов состояния равновесия грубые, их характер не изменяется при достаточно малых изменениях правых частей Ур.23. При этом малыми должны быть изменения не только правых частей, но и их производных первого порядка. Шестое состояние равновесия – центр – негрубое. При малых изменениях параметров правой части уравнений он переходит в устойчивый или неустойчивый фокус.
Замечание. Важно понимать, что математика не позволяет решению достигать положения равновесия за конечный промежуток времени; при
t→∞; решение асимптотически стремится к равновесию, но не достигает его. Даже в очень большие времена всегда есть очень небольшое остаточное движение. Это противоречит реальным физическим системам, которые достигают равновесия
Рассмотрим автономные системы u F(u) , правые части которых непрерывно дифференцируемы, что обеспечивает единственность решений исходной задачи. Если любое решение, начинающееся вблизи данного равновесного решения, стремится к нему, то равновесие называется асимптотически устойчивым. Если решения, которые стартуют вблизи точки равновесия и постоянно находятся вблизи этой точки, то равновесие стабильно.
Устойчивость скалярного обыкновенного дифференциального уравнения первого порядка определить легко, поскольку все неравновесные решения u(t) – строго монотонные функции: они либо всегда увеличиваются, либо всегда уменьшаются. Действительно, если F(u)>0, то производная u>0 и, следовательно, u(t) возрастает в такой точке, и, наоборот, решения убывают в любой точке, если F(u)<0.
Теорема. Точка равновесия u автономного скалярного дифференциального уравнения асимптотически устойчива тогда и только тогда, когда F(u)>0 для u - δ<u<u и F(u)<0 для u <u<u +δ, для некоторого δ>0.
Знак функции F(u) вблизи равновесия определяет её устойчивость. В большинстве случаев это можно проверить, посмотрев на производную функции при равновесии. Если F'(u )<0, то система устойчива (F(u) переходит с положительного в отрицательный с ростом u), но если F'(u )>0, то равновесие u неустойчиво по обе стороны от точки равновесия.
http://profbeckman.narod.ru/
Теорема. Пусть u – точка равновесия для скалярного обыкновенного дифференциального уравнения u=F(u). Если F'(u )<0, то u асимптотически устойчиво. Если F'(u )>0, то u неустойчиво.
Устойчивость (и асимптотическая устойчивость) стационарных решений (особых точек) – локальное свойство векторного поля, задающего систему дифференциальных уравнений. Просто стремление решений к положению равновесия при t не является локальным свойством и недостаточно для асимптотической устойчивости.
Устойчивая гиперболическая особая точка всегда экспоненциально асимптотически устойчива.
Теорема. Особая точка дифференцируемого векторного поля, для которой
|
d |
m |
V dx |
m |
V |
Fk x 0 устойчива. |
||
существует функция Ляпунова |
|
V (x) |
|
|
k |
|
|
|
dt |
x |
dt |
x |
|||||
|
|
k 1 |
k |
k 1 |
k |
|
||
Устойчивость особой точки определяется корнями характеристического уравнения. От корней характеристического уравнения системы зависит форма фазовых траекторий. Особой точке в зависимости от корней характеристического уравнения присваивается имя собственное:
1.два действительных отрицательных корня – устойчивый узел.
2.два действительных положительных корня – неустойчивый узел.
3.два комплексных корня в левой полуплоскости – устойчивый фокус.
4.два комплексных корня в правой полуплоскости – неустойчивый фокус.
5.два мнимых корня – центр.
6.два действительных корня. Один – положительный, другой – отрицательный – седло (как следует из теоремы Гробмана-Хартмана, седло всегда неустойчиво).
Если нет интегральных кривых, входящих в особую точку, то особая точка называется точкой устойчивого типа. Окрестность устойчивой особой точки состоит из замкнутых интегральных кривых, содержащих особую точку внутри себя, между которыми расположены спирали.
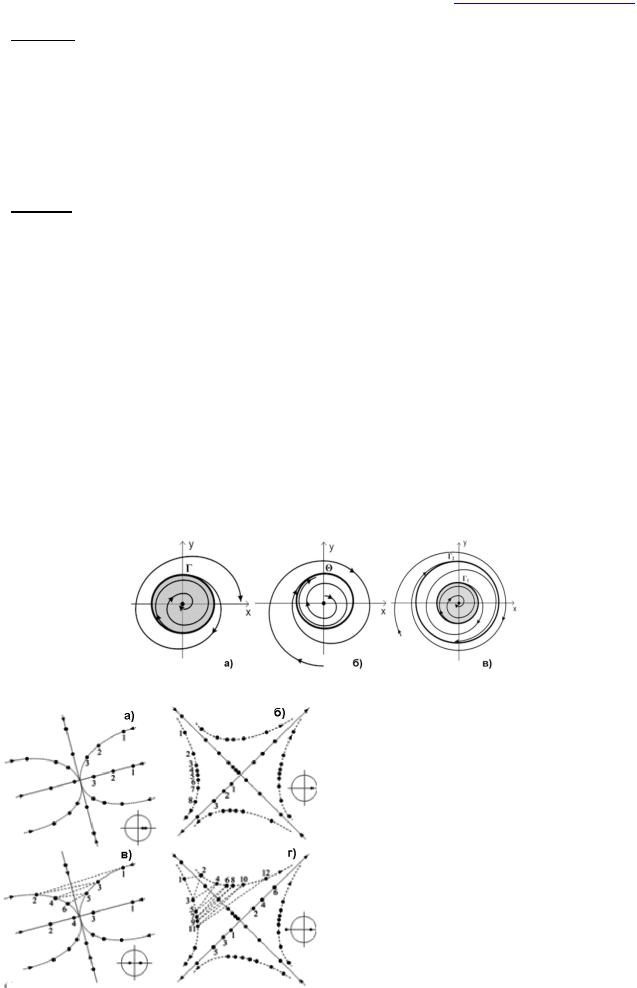
Рис. 17. Особые точки: а – устойчивый фокус – неустойчивый предельный цикл; б – неустойчивый фокус – устойчивый предельный цикл; в – неустойчивый предельный цикл – устойчивый предельный цикл.
Рис. 18. Фазовые диаграммы с вещественными собственными значениями:
(a) и (в) устойчивые узлы; (б) и (г) седловые точки.
Область притяжения точки покоя ограничена неустойчивым предельным циклом Г (рис. 17а) – чисто математическая абстракция. Рис. 17б – в системе при любых начальных условиях имеют место автоколебания, соответствующие устойчивому предельному циклу . Система, фазовый портрет которой
