http://profbeckman.narod.ru/

равновесия характерна секторная структура: эллиптический сектор; гиперболический сектор (седло); параболический сектор (типа аттрактор или репеллер).

Рис. 4. Фазовый портрет. Положения равновесия u1 и u2 – неустойчивы, u3 – асимптотически устойчиво, u4 – полуустойчиво

Обычно рассматривается задача об устойчивости тривиального решения в особой точке, поскольку задача об устойчивости произвольной траектории сводится к данной путём замены неизвестной функции.

Как уже упоминалось, все линейные однородные системы второго порядкаx ax by

(detA 0) (1)

y cx dy

можно разбить на группы, положив в основу классификации поведение их траекторий. При этом в центре внимания оказывается нулевое решение (положение равновесия (0;0)). Возможны три случая:

1.Существует траектории, двигаясь по которым точка при t уходит от положения равновесия (неустойчивые узлы, седло, неустойчивые фокусы).

2.Двигаясь по любой траектории, точка остаётся в некоторой окрестности (может быть

достаточно большой) точки равновесия, не стремясь к ней при t (центр).

3. Двигаясь по любой траектории, точка t стремится к положению равновесия (устойчивые узлы и фокусы).

Впервом случае нулевое решение неустойчиво, во втором - устойчиво, и в третьем

-асимптотически устойчиво.

14.2Устойчивость по Ляпунову (метод первого приближения)

Впонятии устойчивость по Ляпунову реализуется идея малых отклонений решения дифференциального уравнения на промежутке времени [0,+ ] при небольших вариациях начальных данных этого решения.

Ляпунов разделил методы теории устойчивости на два класса. К первому он отнёс те методы, которые при своём применении требуют определённую информацию о решениях исследуемой системы. Такой подход называется первым методом Ляпунова.

Выделяют два типа устойчивости.

1) Устойчивость относительно возмущения начальных данных. К ним относятся: устойчивость по Ляпунову, устойчивость по Пуанкаре (орбитальная устойчивость, устойчивость по Жуковскому, практическая устойчивость и неустойчивость, устойчивость относительно части переменных и условная устойчивость).

2) Устойчивость относительно постоянно действующих внешних возмущений.

В математической теории систем вектор состояния обозначают через x(t), а уравнение движения системы записывают в виде

dt

Фактически это система дифференциальных уравнений первого порядка, в нём правая часть зависит только от значений t и x(t) , но не от производных. Если вектор состояния x(t) состоит из двух компонентов, x1(t) и x2(t), то x1 f1(x), x2 f2 (x) , где

функции f1(x,t) и f2(x,t) зависят от вектора состояния и времени.

Устойчивость определяется для некоторого положения равновесия. Для нелинейной системы может быть несколько положений равновесия, причем некоторые из них могут быть устойчивы, а некоторые – нет. В положении равновесия все производные равны нулю. Предположим, что систему вывели в некоторое начальное состояние x=x(0) (задали

http://profbeckman.narod.ru/

начальные условия), а потом внешнее воздействие прекратили. Дальнейшее изменение координат системы x(t)) можно найти как решение ОДУ при заданных начальных условиях. Устойчивость означает, что все движения x(t), которые начинаются близко от положения равновесия x0, при всех t остаются в некоторой окрестности x0. Если система не просто устойчива, а еще и возвращается в положение равновесия, т. е. x(t) стремится к x0 при t→∞, то говорят об асимптотической устойчивости.

Известны различные определения устойчивости: устойчивость по Ляпунову, асимптотическая устойчивость экспоненциальная устойчивость и др. Критериев устойчивости тоже много: Ляпунова, Рауса-Гурвица, Найквиста, Михайлова и др.

Ограничимся рассмотрением устойчивости по Ляпунову.

Для исследования устойчивости систем существует два варианта метода Ляпунова. Первый основан на определении корней характеристического уравнения системы обыкновенных дифференциальных уравнений, описывающей физико-химическую систему, а второй метод – на исследовании физико-химической системы с помощью скалярной функции Ляпунова. Основным преимуществом метода функций Ляпунова

перед всеми остальными подходами к решению разнообразных задач устойчивости является его универсальность. Это единственный метод анализа устойчивости динамических систем любого нелинейного вида и любой размерности.

Рис. 5. Иллюстрация к определению устойчивости области и на плоскости (х,у).

Проиллюстрируем особенности первого метода на примере простой линейной системе первого порядка, с одной переменной состояния x(t): x'=f(x). Предположим, что

это уравнение имеет положение равновесия, причём оно находится в начале координат. Тогда устойчивость положения равновесия – это равномерная на интервале t>0 сходимость (к постоянному значению) решений, начальные значения которых стремятся к рассматриваемому положению равновесия. В двумерном случае состояние равновесия устойчиво, если для любой заданной области ( ) допустимых отклонений от состояния равновесия (например, область вокруг точки равновесия на рис. 5) можно указать область ( ), окружающую состояние равновесия и обладающую тем свойством, что ни одна траектория, которая начинается внутри области , никогда не достигнет границы .

Устойчивое состояние равновесия характеризуется тем, что отклонение от этого состояния не превысит сколь угодно малой величины, если начальное возмущение достаточно мало. Если возникающее малое отклонение с течением времени затухает, то такое равновесие называется асимптотически устойчивым. Следовательно, если малые начальные отклонения приводят к возникновению достаточно малых периодических колебаний в системе, состояние равновесия устойчиво, но не асимптотически. Или более строго: система устойчива по Ляпунову в положении равновесия x0, если при начальном отклонении от положения равновесия x(0) не более, чем на δ, траектория движения отклоняется от x0 не более, чем на ε, причём для каждого ε можно найти соответствующее ему δ(ε): |x(0)-x0|<δ и |x(t)-x0|<ε при всех t>0. Это означает, что чем меньше начальное отклонение, тем меньше траектория движения отклоняется от положения равновесия.

Если, кроме того, вектор состояния стремится к положению равновесия, т. е. |x(t)- x0| 0 при t , система называется асимптотически устойчивой в положении равновесия x0.

Положение равновесия x0 называется асимптотически устойчивым, если оно устойчиво по Ляпунову и предел х(t) при t равен нулю для всякого решения х с начальным условием х(0), лежащим в достаточно малой окрестности нуля.

http://profbeckman.narod.ru/

Заметим, что выполнение условия сходимости не гарантирует устойчивость по Ляпунову. Существуют примеры достаточно сложных нелинейных систем, в которых даже при очень малых отклонениях от положения равновесия сначала наблюдается большой «выброс», а затем траектория сходится к точке равновесия. Асимптотическая устойчивость – более сильное требование. Положения равновесия, которые устойчивы по Ляпунову, но не асимптотически устойчивы, называются нейтрально устойчивыми (маятник без трения, бассейн с водой).

Абсолютная устойчивость - устойчивость, при которой начальные отклонения не только не нарастают, но затухают, стремясь к нулю.

Положение равновесия неустойчиво, если для него не выполняется условие устойчивости Ляпунова. Это значит, что существует такое ε>0 , что траектория x(t) выходит за границы области |x(t)-x0|<ε при сколь угодно малом отклонении начального состояния x(0) от положения равновесия x0. Например, система переходит в другое положение равновесия, или x(t) неограниченно возрастает.

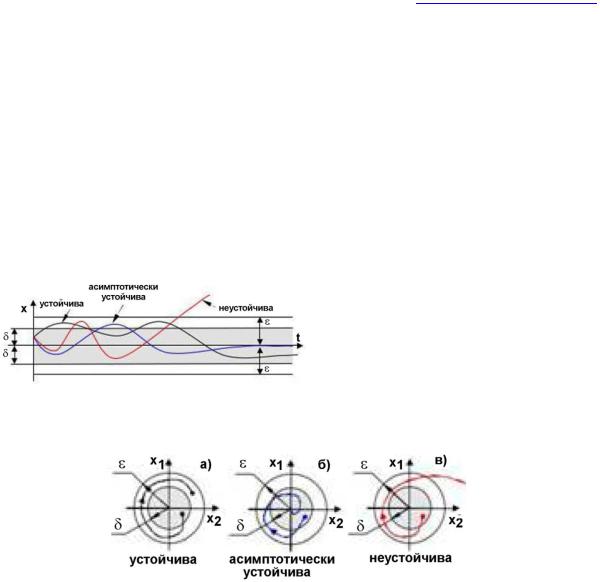
Рис. 6. Движения устойчивой, асимптотически устойчивой и неустойчивой систем первого порядка (с одной координатой x(t)).

Траекторию движения систем второго порядка обычно изображают на фазовой плоскости. На рис. 7 показаны движения устойчивой, асимптотически

устойчивой и неустойчивой систем. Для простоты предполагается, что положение равновесия – это начало координат, где x1=x2=0.

Рис.7. Фазовые траектории систем различной устойчивости.

Линейные системы обладают рядом особенностей, которые во многих случаях упрощают анализ устойчивости:

-автономная линейная система (на которую не действуют внешние силы) может иметь единственное положение равновесия (в котором все сигналы равны нулю) или бесконечно много положений равновесия (шарик на плоской поверхности);

-устойчивость – это свойство линейной системы, а не отдельного положения равновесия: или все ее движения устойчивы (асимптотически устойчивы), или все неустойчивы;

-асимптотическая устойчивость линейной системы «в малом» сразу означает ее устойчивость «в целом», то есть, при любых отклонениях от положения равновесия;

-асимптотически устойчивая система также обладает устойчивостью «вход-выход»,а просто устойчивая (нейтрально устойчивая, не асимптотически устойчивая) – нет.

Для проверки устойчивости системы в уравнение стационарного состояния системы вводят возмущение и затем исследуют решение нового уравнения. Если оно стремится к решению, соответствующему стационарному состоянию, – система устойчива, в противном случае – неустойчива. Стационарное состояние линейной

х0 – значения функции, соответствующие стационарному состоянию, a f(t) – либо постоянная величина, либо периодическая функция. При изучении устойчивости «в малом» системе нужно сообщить некоторое возмущение х, которое может быть сколь

http://profbeckman.narod.ru/

угодно малым по величине. Это возмущение вызовет изменение зависимой переменной. Уравнение примет вид

Решение первого уравнения соответствует стационарному режиму, в котором система находилась до возмущения. Второе уравнение соответствует системе, находящейся в свободном режиме, и его решение однозначно отвечает на вопрос об устойчивости системы. Если свободный процесс имеет характер затухающего колебания, система устойчива, если нарастающего – неустойчива. Таким образом, задача сводится к рассмотрению однородного Ур.4. В этом уравнении и далее будем считать, что аm>0. Решение Ур.4 имеет вид

где Ai – постоянные, определяемые из начальных условий, а i – корни характеристического уравнения:

D( )=am m+am-1 m-1+...+a1 +a0=0. (6)

Характеристическое Ур.6 в общем случае может обладать как вещественными корнями i= i, так и парами комплексно сопряжённых корней: i= i+i i. Если среди общего числа m корней действительными окажутся n корней и пар комплексно сопряжённых, то решение можно представить в виде суммы n экспоненциальных и =(m- n)/2 осциллирующих членов:

сопряжёнными корнями.

Характер процессов может оказаться весьма сложным. В общем случае изменение х происходит по апариодическому закону, на который накладываются процессы колебательного характера с нарастающими, затухающими или неизменными амплитудами различных частот. Отклонение, вызванное апериодическим слагаемым с i>0, монотонно

возрастают, а с l<0 – монотонно уменьшаются. Аналогично амплитуда Сj e jt каждого

колебательного процесса с течением времени неограниченно возрастает, если j>0, и затухает, если j<0.

Система является устойчивой, если все слагаемые с течением времени затухают,

т.е. показатели экспонент имеют отрицательные знаки: e i t , e j t . Система является устойчивой, если все вещественные корни и вещественные части всех комплексно сопряженных корней характеристического уравнения отрицательны. Если хотя бы один корень (или его вещественная часть) будет положительным, т. е. появится слагаемое вида

При некоторых комбинациях коэффициентов ai все корни характеристического уравнения имеют отрицательные вещественные части. Полезно установить соотношения, при которых это имеет место, ибо тогда можно будет судить об устойчивости состояния