http://profbeckman.narod.ru/

одна интегральная кривая не проходит через начало координат. Такая особая точка называется седлом. Где бы ни находилась изображающая точка в начальный момент (за исключением начала

координат и асимптоты y k х , она всегда, в конце концов, будет удаляться от начала

координат, причём движение будет носить апериодический характер, а не колебательный. Положение равновесия, соответствующее особой точке типа седла, всегда будет неустойчивым,

ввиду того, что движение по асимптоте y k х не может быть никогда точно реализовано, так как вероятность начального состояния, соответствующего движению к особой точке, равна нулю.

Рис. 16. Фазовые траектории линейной системы линейных уравнений ОДУ второго порядка.

Рис. 17. Фазовые диаграммы для линейных систем уравнений второго порядка.

12.2 Классификация точек равновесия

Простейшими примерами особых точек являются особые точки линейных векторных полей на плоскости. С понятием векторного поля на плоскости можно связать линейную систему дифференциальных уравнений вида:

x Ax, (9)

где х=х(х1, х2) – точка на плоскости, – матрица. Очевидно, что точка в случае невырожденной матрицы является единственной особой точкой такого уравнения.

При классификации критических точек сначала находят собственные значения

http://profbeckman.narod.ru/

1.Если собственные значения действительны и различны, то критическая точка является, либо узлом, либо седлом.

– Если оба собственных значения положительны, то критическая точка является неустойчивым узлом; траектории касаются собственного вектора, связанного с меньшим собственным значением.

– Если оба собственных значения отрицательны, критическая точка является устойчивым узлом; траектории касаются собственного вектора, связанного с численно меньшим собственным значением.

– Если собственные значения имеют противоположный знак, критическая точка является седлом; траектории асимптотически приближаются к собственному вектору, связанному с положительным собственным значением.

2.Если собственные значения не являются вещественными и имеют вид + i, критическая точка является либо спиральной точкой, либо центром.

–Если >0, критическая точка является неустойчивой спиральной точкой.

–Если <0, критическая точка является устойчивой спиральной точкой.

–Если =0, критическая точка - это центр.

Во всех трех случаях движение по часовой стрелке, если b-c положительно и против часовой стрелки, если оно отрицательно.

3. Если собственные значения действительны и повторяются, то критическая точка является либо звездой, либо вырожденным узлом. Если матрица кратно единичной матрице, то она является звездой; если нет, это неправильный узел. Если собственное значение положительно, критическая точка неустойчива; если он отрицательно, оно стабилено. В случае неправильных узлов траектории касаются единственного собственного вектора. Если b-c положительно, движение идёт по часовой стрелке; если отрицательный, против часовой стрелки.

Знаки собственных значений определяет поведение фазовых траекторий:

–Если знаки противоположны, то пересечение собственных векторов является седлом.

–Если знаки оба положительные, то собственные векторы представляют собой стабильные ситуации, в которых система расходится, а пересечение траекторий – неустойчивый узел.

–Если знаки оба отрицательные, то собственные векторы представляют собой стабильные ситуации, в которых система сходится, а пересечение траекторий – устойчивый узел.

Различные фазовые траектории одной достаточно гладкой динамической системы не пересекаются в фазовом пространстве. Фазовые траектории могут представлять собой либо отдельные точки, либо замкнутые кривые, либо отрезки кривых конечной длины, заключённые между двумя точками (последние не принадлежат данной траектории), либо кривые, неограниченные в одну или обе стороны. Траектории, являющиеся точками, называются особыми точками и отвечают стационарным состояниям динамической системы.

Двумерные линейные системы классифицируются следующим образом:

1. Два действительных собственных значения. Неподвижная точка – узел. Случай совпадающих корней: жорданов узел (одна жорданова клетка) и дикритический узел (две жордановы клетки).

2. Два комплексно-сопряженных корня с ненулевой действительной частью. Фокус.

3. Два действительных собственных значения разных знаков. Седло. Сепаратрисы. Устойчивое и неустойчивое подпространства.

4. Два комплексно-сопряженных чисто мнимых корня. Центр. 5. Вырожденный случай: нулевое собственное значение.

Классификация трёхмерных систем:

http://profbeckman.narod.ru/

1.Устойчивый (неустойчивый) узел – три действительных корня одного знака или один действительный и два комплексных с тем же знаком действительной части и с ведущим действительным корнем.

2.Устойчивый (неустойчивый) фокус – один действительный и два комплексных с ведущими комплексными.

3.Седло-фокус – устойчивое одномерное подпространство и неустойчивое двумерное типа фокус, также наоборот.

Многомерные системы. Жорданова нормальная форма. Инвариантные подпространства.

Табл.1. Классификация точек равновесия

В зависимости от собственных значений матрицы А, различают пять типов невырожденных особых точек линейных систем: узел (node), седло (saddle), фокус (spiral) - гиперболические равновесия и центр (center) - негиперболическое равновесие.

Устойчивость положений равновесия определяется общими теоремами об устойчивости. Так, если действительные собственные значения (или действительные части комплексных собственных значений) отрицательны, то точка равновесия является асимптотически устойчивой. Примерами таких положений равновесия являются устойчивый узел и устойчивый фокус. Если действительная часть хотя бы одного собственного числа положительна, то соответствующее положение равновесия является неустойчивым. Например, это может быть седло. Наконец, в случае чисто мнимых корней (точка равновесия является центром) имеет место классическая устойчивость в смысле Ляпунова.

Как уже упоминалось, общее решение системы Ур.1 имеет вид:

X(t)=C1e 1tV1+C2e 2tV2,

где V1 и V2 – собственные векторы, соответствующие числам 1 и 2, а С1, С2 – произвольные константы.

Рассмотрим подробнее каждый тип точки равновесия и соответствующие фазовые портреты.

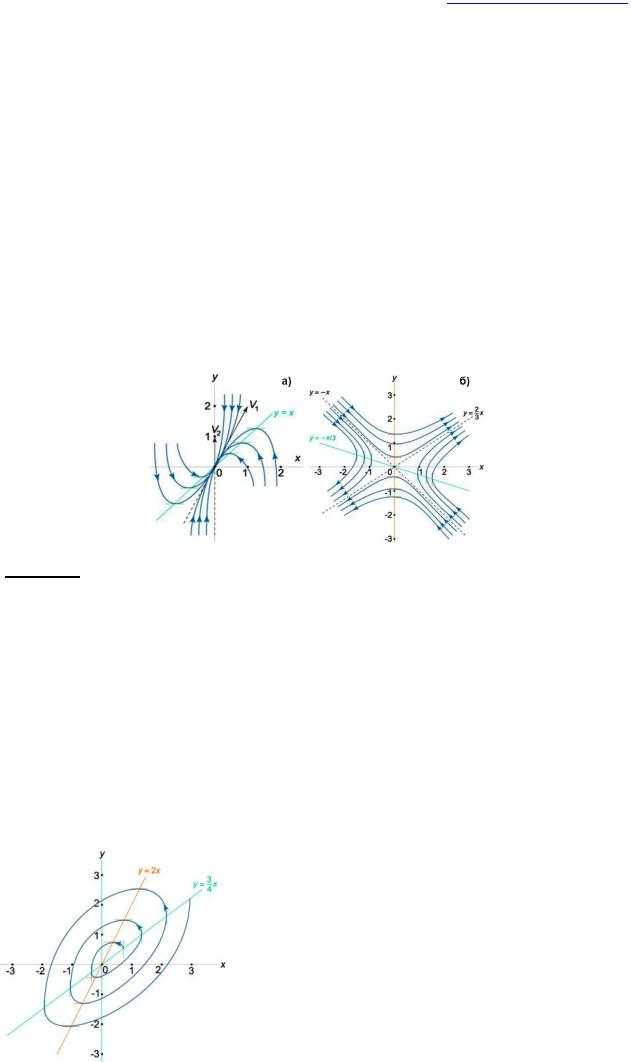
Узел - положение равновесия при условии, что корни Ур.1 1 и 2 – вещественны, различны (1 2) и имеют один и тот же знак; может быть устойчивым и неустойчивым. Устойчивый узел – точка равновесия, в которую входят все интегральные кривые, проходящие через точки достаточно малой окрестности узла. Корни Ур.1 отрицательны (1<0, 2<0), 1 2>0. Через узел проходит бесконечное множество интегральных кривых. Фазовые траектории имеют вид парабол. Поскольку оба собственных значения 1 и 2, отрицательны, то решение Х=0 является асимптотически устойчивым. При t фазовые траектории стремятся к особой точке (начало координат Х=0) со своей касательной. Приняв х0 за центр круга можно выбрать его радиус настолько малым, чтобы каждая характеристика входящая в этот круг извне приближалась к х0 с определенной касательной. Если С10, то при t фазовые траектории параллельны собственному вектору V1, если С1=0, то фазовая траектория лежит на прямой, направленной вдоль собственного вектора V2. При t - и при С20 фазовые кривые становятся

http://profbeckman.narod.ru/

параллельными вектору V2, а при С2=0 фазовая траектория определяется направлением собственного вектора V1. Для устойчивого узла собственное значение ( ) с минимальным абсолютным значением действительной части называется принципом или ведущим; когда собственные значения различны, все орбиты, кроме двух, стремятся к узлу вдоль ведущего собственного вектора (картина инвертируется для неустойчивого узла).

Неустойчивый узел – фазовые траектории выходят из точки х0. Корни λ1,λ2 различны

(λ1≠λ2) и положительны (λ1>0,λ2>0).

Замечание. В случае как устойчивого, так и неустойчивого узла фазовые траектории касаются прямой, которая направлена вдоль собственного вектора, соответствующего меньшему по абсолютной величине собственному значению λ.

Дикритический узел Пусть характеристическое уравнение имеет один нулевой корень кратности 2, λ1=λ2=λ≠0. При этом система имеет базис из двух собственных векторов, т.е. геометрическая кратность собственного значения λ равна 2. Такая ситуация реализуется в системах вида dx/dt=λx, dy/dt=λy. Направление фазовых траекторий зависит от знака λ. Здесь возможны следующие два случая:

Случай λ1=λ2=λ<0. Такое положение равновесия называется устойчивым дикритическим узлом.

Случай λ1=λ2=λ>0. Данная комбинация собственных значений соответствует

неустойчивому дикритическому узлу.

Здесь все интегральные кривые проходят через начало координат с определённым направлением касательных; коэффициенты этих касательных могут иметь все возможные значения.

Рис. 18. Точка равновесия – узел: а – устойчивый, б – неустойчивый.

Рис. 19 . Докритический узел (звезда): а – устойчивый, б – неустойчивый.

Рис. 20. Вырожденный узел: а – устойчивый, б – неустойчивый.

Вырожденный узел. Пусть собственные значения матрицы A снова являются совпадающими: λ1=λ2=λ≠0. В отличие от предыдущего случая дикритического узла предположим, что геометрическая кратность собственного значения (или другими

http://profbeckman.narod.ru/

словами размерность собственного подпространства) равна теперь 1. Это означает, что матрица A имеет лишь один собственный вектор V1. Второй линейно независимый вектор, необходимый для составления базиса, определяется как вектор W1, присоединенный к V1. В случае λ1=λ2=λ<0 точка равновесия называется устойчивым вырожденным узлом. При λ1=λ2=λ>0 положение равновесия называется неустойчивым вырожденным узлом.

Особые точки могут быть устойчивыми и неустойчивыми. Однако, даже в случае двух функций x(t), y(t), т.е. фазового портрета на плоскости, может наблюдаться чуть более сложное сочетание. Одна и та же особая точка может быть устойчива, например, по x(t), и неустойчива по y(t). Такую особую точку называют

седлом.

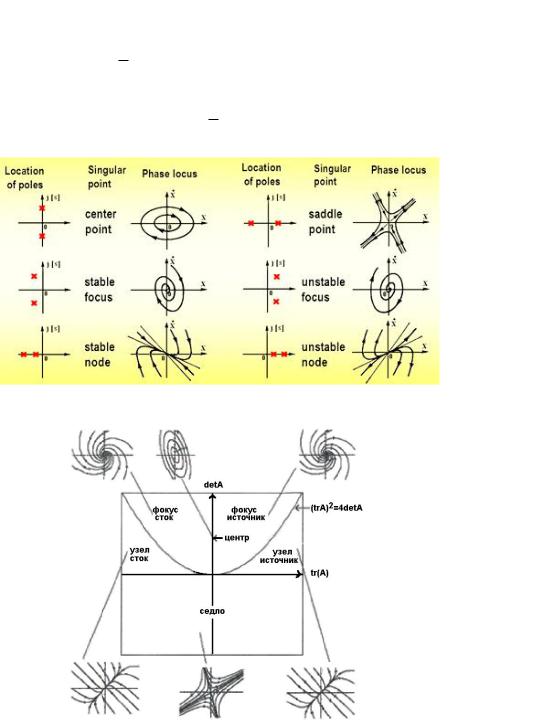
Рис. 21. Точка равновесия - седло.

Седло – положение равновесия при условиях λ1,λ2 R, λ1≠λ2, λ1 λ2<0; собственные значения действительны и имеют противоположные знаки. Это

– негиперболическое равновесие. Седло всегда неустойчиво. В окрестности седла четыре интегральные кривые (сепаратрисы) входят в особые точки, а между ними располагаются интегральные кривые типа гипербол. Поскольку одно из

собственных значений положительно, то седло является неустойчивой точкой равновесия. Если λ1<0, λ2>0, то собственные значения λ1 и λ2 ассоциируются с соответствующими собственными векторами V1 и V2. Прямые, направленные вдоль собственных векторов V1, V2, называются сепаратрисами. Они являются асимптотами для остальных фазовых траекторий, имеющих форму гипербол. Каждой из сепаратрис можно сопоставить определенное направление движения. Если сепаратриса связана с отрицательным собственным значением λ1<0, т.е. направлена вдоль вектора V1, то движение вдоль нее происходит к точке равновесия X=0. И наоборот, при λ2>0, т.е. для сепаратрисы, связанной с вектором V2, движение направлено от начала координат. Траектории имеют вид гипербол (асимптоты к ним – прямые линии). Число характеристик оканчивающихся в седле всегда конечное и чётное. Каждая из них имеет два продолжения. Область, ограниченная двумя соседними характеристиками, оканчивающимися в особой точке, есть область отталкивания. Если положение равновесия является седлом, то существуют фазовые траектории, лежащие на прямых, проходящих через начало координат. Движение по одной из его сепаратрис происходит в направлении начала координат, по другой – от начала координат. По всем другим фазовым траекториям движение происходит в соответствии с движением по сепаратрисам.

Сепаратриса – траектория динамической системы с двумерным фазовым пространством, стремящаяся к седловому состоянию равновесия при времени t (устойчивая сепаратриса) или при t - (неустойчивая сепаратриса). Если сепаратриса стремится к седлу при t + , то её (вместе с седлом) называют петлей

сепаратрисы.

Рис. 22. Особая сингулярная точка

Если положение равновесия – седло, то достаточно установить направление движения по любой одной траектории, а дальше можно однозначно установить направление движения по всем остальным. Если x(t) 0 при t + , то движение по сепаратрисе y=kx идёт в

направлении точки равновесия. Если x(t) 0 при t + ,то движение по сепаратрисе у=kx идёт от точки равновесия.

http://profbeckman.narod.ru/

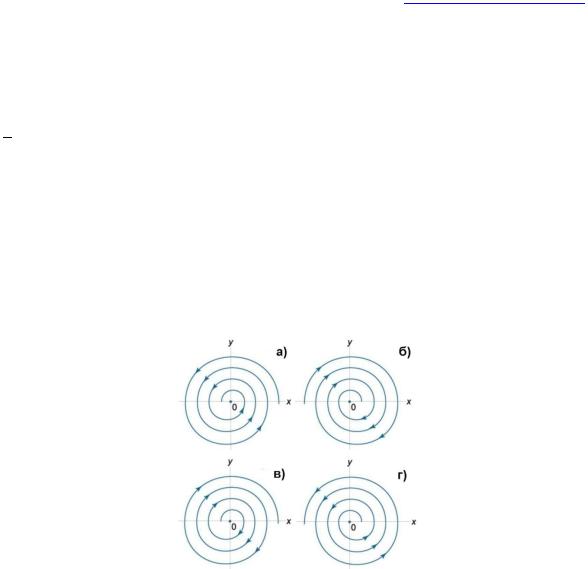
Фокус (спиральная точка) – неподвижная точка имеет место, если собственные значения 1, 2 являются комплексными числами, действительные части которых не равны нулю (1 и 2 – комплексные, но не чисто мнимые), т.е. когда собственные значения комплексно сопряжены. Если матрица А состоит из действительных чисел, то комплексные корни будут представлены в виде комплексно-сопряженных чисел:1,2=+i, α≠0 и β≠0. Все интегральные кривые, проходящие через точки достаточно малой окрестности фокуса, представляют собой спирали с бесконечным числом витков в любой сколь угодно малой окрестности фокуса (всякая интегральная кривая бесконечное число раз закручивается вокруг фокуса). Это – семейство логарифмических спиралей с асимптотической точкой в начале, но без предельной касательной; они делают около точки (0,0) бесконечное число оборотов.

Комплексное решение Х1(t) соответствующее собственному числу 1=+i имеет

вид:

где V1=U+iW − комплекснозначный собственный вектор, ассоциированный с числом λ1, U и W − действительные векторные функции.

Рис. 23. Равновесная точка – фокус: а – устойчивый, с>0; б – устойчивый, c<0; в

– неустойчивый, с<0; г – неустойчивый, с>0.

Представим постоянные C1,C2 в виде C1=Csinδ, C2=Ccosδ, где δ − некоторый вспомогательный угол. Решение X(t) раскладывается по базису, заданному векторами и W: X(t)=μ(t)U+η(t)W, где коэффициенты разложения μ(t), η(t) определяются формулами: μ(t)=Ceαtsin(βt+δ),η(t)=Ceαtcos(βt+δ). Фазовые траектории представляют собой спирали. При α<0 спирали будут закручиваться, приближаясь к началу координат. Такое положение равновесия называется устойчивым фокусом. Соответственно, при α>0 будет неустойчивый фокус. Направление закручивания спиралей можно определить по знаку коэффициента с в исходной матрице A. Действительно, рассмотрим производную dy/dt, например, в точке (1,0): dy/dt(1,0)=с 1+d 0=c. Положительный коэффициент c>0 соответствует закручиванию спиралей против часовой стрелки. При c<0 спирали будут закручиваться по часовой стрелке. С учётом направления закручивания спиралей, всего существует 4 различных вида фокуса. При определённых условиях (например, при малом коэффициенте трения колебательной системы) фокус превращается в центр – колебания становятся периодическими.

Устойчивый фокус – все фазовые траектории при приближении к особой точке спиралеобразно закручиваются вокруг неё в одном и том же направлении (спиральный сток). Фокус стабилен, когда собственные значения имеют отрицательную действительную часть Спираль закручивается либо о часовой стрелке или против нее (направление закрутки определяется знаком производной y'(t) в точках оси х. Фазовые

http://profbeckman.narod.ru/

траектории оканчиваются в неподвижной точке, но ни одна из них не оканчивается определённой касательной.

Неустойчивый фокус – фазовые траектории по спирали уходят от особой точки и уходят в бесконечность (спиральный источник). Фокус не устойчив, когда собственные значения положительную действительную часть.

Особые точки типа фокус и узел дают примеры аттракторов, к которым притягиваются все фазовые траектории.

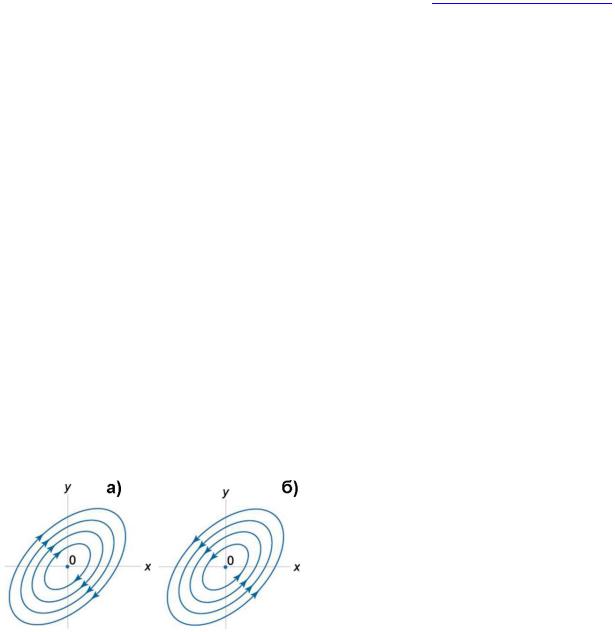
Центр – положение равновесия, в случае, когда собственные значения матрицы A являются число мнимыми числами. Для матрицы с действительными элементами мнимые собственные значения будут комплексно-сопряженными. Фазовый портрет, соответствующий особой точке центр, представляет собой бесконечное семейство вложенных друг в друга замкнутых кривых – эллипсов с центром в начале координат. Фазовый портрет для особой точки типа центр представляет собой простейший пример бесконечного семейства консервативных движений.

В случае центра фазовые траектории формально получаются из уравнения спиралей при α=0 и представляют собой эллипсы, т.е. описывают периодическое движение точки на фазовой плоскости. Фазовые траектории описывают замкнутые эллипсы или окружности вокруг неподвижной точки в начале координат, ни одна фазовая траектория не проходит через особую точку. Движение может идти. При определённых условиях центр может трансформироваться в фокус. Положения равновесия типа "центр" являются устойчивыми по Ляпунову.

Возможны два вида центра, различающиеся направлением движения точек (по часовой стрелке или против нее). Как и в случае спиралей, направление движения можно определить, например, по знаку производной dy/dt в какой-либо точке. Если взять точку

(1,0), то dy/dt(1,0)=с, т.е. направление вращения определяется знаком коэффициента с.

Рис. 24. Равновесная точка – центр: а – c<0; б – c>0.

Итак, мы рассмотрели различные типы точек равновесия в случае

невырожденной матрицы A(detA≠0).С

учётом направления фазовых траекторий всего существует 13 различных фазовых портретов.

Теперь обратимся к случаю вырожденной матрицы A.

Случай 1 2=0 представляют предмет более глубокого исследования. Если 1 и 2 – чисто мнимые корни, λ1,2=±iβ, β≠0, то особая точка может быть фокусом или центром, а может иметь и более сложный характер.

Если матрица является вырожденной, то у неё одно или оба собственных значения

равны нулю. При этом возможны следующие частные случаи:

Случай λ1≠0, λ2=0. Здесь общее решение записывается в виде X(t)=C1eλ1tV1+C2V2, где V1, V2, − собственные векторы, соответствующие числам λ1 и λ2. Ванном случае вся прямая, проходящая через начало координат и направленная вдоль вектора V2, состоит из точек равновесия (эти точки не имеют специального названия). Фазовые траектории представляют собой лучи, параллельные другому собственному вектору V1. В зависимости от знака λ1 движение при t→∞ происходит либо в направлении прямой V2, либо от нее.

Изобразим на плоскости собственные векторы V1, V2, горизонтальную изоклину y=x и построим схематический фазовый портрет системы (рис. 27). Фазовые траектории будут приближаться к нулю, касаясь прямой, направленной вдоль вектора V1, поскольку этому собственному вектору соответствует наименьшее по модулю собственное значение | 1|=1.

Рис. 27. К примерам 15(а) и 16 (б).

Пример 16. Исследовать положения равновесия динамической системы dx/dt=x+3y, dy/dt=2x и

равновесия в начале координат. Решим данную задачу без вычисления собственных значений и собственных векторов. Поскольку определитель detA<0, то нулевое положение равновесия является cедлом. Определим уравнения изоклин. Вертикальная изоклина описывается следующей линейной функцией: dx/dt=x+3y=0, y=−х/3. Уравнение горизонтальной изоклины имеет вид: dy/dt=2x=0, x=0 (ось Oy). Найдём уравнение сепаратрис, которое имеет вид y=kx. Подставляя это в исходную систему, получаем квадратное уравнение для коэффициента k:

Уравнения сепаратрис выглядят так: y=−x, y=(2/3)x. Определим направление движения вдоль фазовых траекторий. Возьмём, к примеру, точку (1,0) и вычислим производную dy/dt в этой точке: dy/dt(1,0)=2 1=2>0. Поскольку производная dy/dt>0, то при увеличении времени t