1.5. Вопросы для самоподготовки к лабораторной работе № п.1

1. Правила выполнения операций с матрицами.

2. Порядок выполнения операций с матрицами в табличном редакторе MS Excel.

3. Названия функций MS Excel выполнения операций с матрицами.

4. Выборочные характеристики статистических признаков. Расчетные формулы.

5. Функции MS Excel (категория «Статистические») для расчета выборочных характеристик статистических признаков.

6. Понятие табличного значения статистического критерия ( критерий, критерий, -критерий) с заданным уровнем значимости и степенями свободы.

7. Функции программы MS Excel, используемые для нахождения значений критерия, критерия, - критерия.

2. Лабораторная работа № 1. Выявление взаимосвязи между статистическими признаками

2.1. Теоретические замечания. Стохастическая природа экономических данных обуславливает необходимость применения статистических методов для их обработки и анализа.

При анализе одного статистического признака, как известно из курса вероятности и математической статистики, рассчитываются такие числовые характеристики как выборочное среднее, дисперсия, стандартное отклонение (табл. 1.3), а также мода, медиана и др.

Основная задача корреляционного анализа – выявление взаимосвязи между двумя или более случайными переменными путем оценки парных, множественных и частных коэффициентов корреляции и проверки их значимости.

Коэффициент парной корреляции рассчитывается по формуле:

Для качественной оценки коэффициента корреляции применяют шкалу Чеддока:

0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-1,0
слабая	заметная	умеренная	высокая	весьма высокая

Для анализа вида связи необходимо построить на плоскости корреляционное поле (диаграмму рассеивания).

Проверка значимости коэффициента парной корреляции, осуществляется с использованием -критерия Стьюдента:

. (2.1)

По таблице выбирается с учетом заданного уровня значимости и числа степеней свободы . Если , то оценка коэффициента корреляции значима (т.е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции отвергается).

Если признаков более двух (например, ), то для анализа корреляционной связи между ними рассчитывают матрицу коэффициентов парной корреляции:

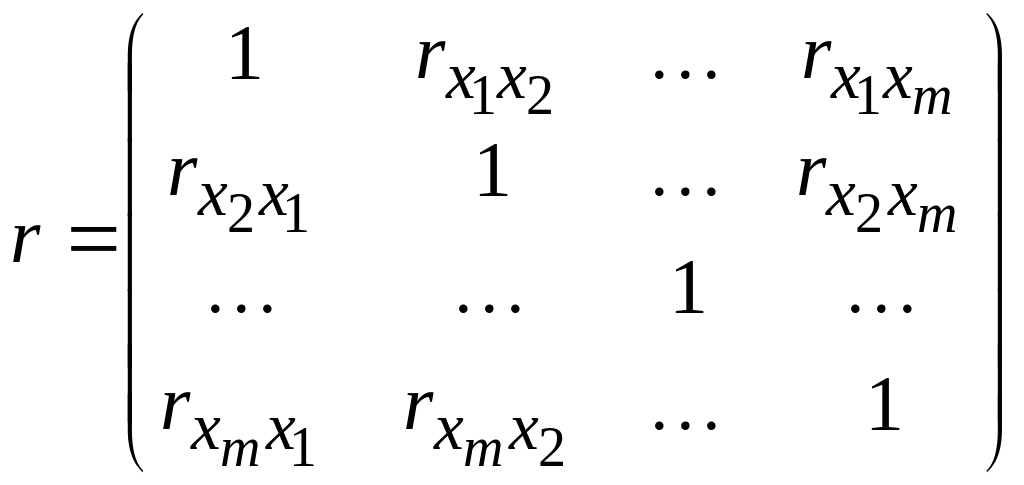. (2.2)

Парные коэффициенты корреляции анализируются, как описано выше. Наличие мультиколлинеарности во всем массиве данных проверяют с помощью критерия Пирсона - . Фактическое значение критерия рассчитывается по формуле:

, (2.3)

где – определитель корреляционной матрицы .

Фактическое значение критерия, рассчитанное по формуле (2.3) сравнивается с табличным значением при степенях свободы и уровне значимости . Если то в массиве переменных существует мультиколлинеарность.

Расчет и проверки значимости коэффициентов множественной и частной корреляции осуществляется на основании значений матрицы - обратной к корреляционной матрице :

Определение тесноты связи одной случайной величины с совокупностью остальных величин, включенных в анализ, решается с помощью выборочного коэффициента множественной корреляции, который вычисляется по формуле:

(2.4)

(2.4^’)

где – определитель корреляционной матрицы , – алгебраическое дополнение элемента матрицы (см. формулу (2.2)), - диагональный элемент матрицы .

Коэффициенты множественной корреляции и детерминации являются величинами положительными, принимающими значения в интервале от 0 до 1.

Проверка значимости коэффициента детерминации осуществляется с помощью -критерия Фишера, расчетное значение которого находится по формуле:

, (2.6)

, (2.6^’)

где коэффициент множественной корреляции, – количество наблюдений, - количество переменных, – диагональный элемент матрицы .

Фактические значения критерия сравниваются с табличным при и степенях свободы и уровне значимости . Если , то соответствующая -ая объясняющая переменная мультиколлинеарна с другими.

По таблице определяется при уровне значимости и степенями свободы и . Если , то значим (значимо отличается от нуля).

Если необходимо определить связь между двумя случайными величинами при исключении влияния остальных, то используется выборочный частный коэффициент корреляции, который вычисляется по формуле:

, (2.7)

(2.7^’)

где – алгебраические дополнения элементов матрицы ,

, , – элементы матрицы .

Частный коэффициент корреляции изменяется, как и парный от –1 до +1. Проверка значимости коэффициента частной корреляции также осуществляется с использованием -критерия Стьюдента.

2.2. Организация данных и расчетов на листе MS Excel. Рассмотрим пример выполнения лабораторной работы № 1. Для выполнения задания 1 нужно создать новую рабочую книгу MS Excel, в ячейки которого ввести исходные данные задачи (рис. 2.1): значения показателей (где - темп роста (уменьшения) реальной заработной платы, в % к соответствующему периоду предыдущего года, %; - уровень безработицы населения (по методологии МОП) в возрасте 15-70 лет, %; - среднемесячная заработная плата, грн.; - индексы потребительских цен; - уровень оплаты населением жилищно-коммунальных услуг (в % к начисленным суммам)).

Рис. 2.1. Организация данных и нахождение корреляционной матрицы показателей средствами программы MS Excel.

Для анализа корреляционной связи между показателями рассчитаем матрицу коэффициентов парной корреляции. Для этого во вкладке «Сервис» вызовем надстройку «Пакет анализа», функция «Корреляция». После этого в поле «Входной интервал» (рис. 2.2) диалогового окна «Корреляция» введем ссылку на ячейки $B$3:$F$29, в которых хранятся значения показателей . В поле «Выходной интервал» (рис. 2.2) введем ссылку на ячейку $J$4, где будет храниться значение коэффициента корреляции и соответственно все элементы корреляционной матрицы будут храниться в ячейках (рис. 2.3).

Для проведения тестов значимости коэффициентов корреляции и мультиколлинеарности в массиве данных выполним расчеты на этом же листе MS Excel (рис. 2.3) по формулам (2.1), (2.3), (2.4), (2.6), (2.7), а также найдем табличные значения соответствующих критериев (табл. 2.1).

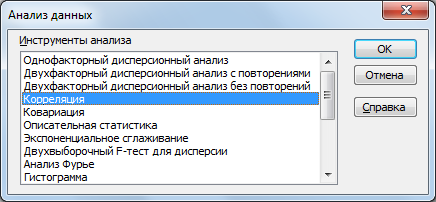
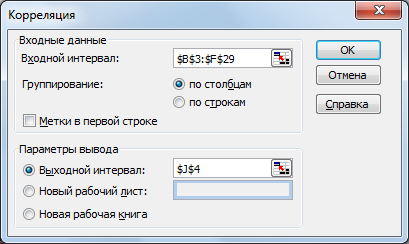
Рис. 2.2. Последовательность операций для расчета матрицы коэффициентов парной корреляции.

2.3. Статистическая проверка значимости парных коэффициентов корреляции. На основании проведенных расчетов сделаем следующие выводы. Так как условие ( ) выполняется для статистик , , то соответствующие коэффициенты парной корреляции , , статистически не значимы. Остальные коэффициенты парной корреляции статистически значимы и на основании шкалы Чеддока, можно сделать вывод, что связь между переменными умеренная.

2.4. Проверка наличия мультиколлинеарности в массиве показателей. Так как то в массиве переменных существует мультиколлинеарность.

2.5. Статистическая проверка значимости выборочных коэффициентов множественной корреляции показателей. Так как условие ( ) выполняется для всех статистик , то делаем вывод (с достоверностью 95%) о статистической значимости коэффициентов множественной корреляции всех показателей и тесной линейной зависимости каждого из факторов с остальными.

2.6. Статистическая проверка значимости выборочных частных коэффициентов множественной корреляции показателей. Так как условие ( ) выполняется только для статистики , то коэффициент частной корреляции статистически значим. Следовательно, между показателем среднемесячной заработной платы, грн. и уровнем оплаты населением жилищно-коммунальных услуг существует тесная линейная зависимость (исключая влияние остальных факторов).

Рис. 2.3. Организация данных и результаты расчетов для проверки значимости коэффициентов корреляции и мультиколлинеарности в массиве данных.

Таблица 2.1.