4.3.8. Мінімізація булевих функцій.

Досконала диз’юнктивна (кон’юнктивна) форма хоч і містить в своїй назві слово «досконала», не є такою для її реалізації електронними схемами. Отримані форми ДДНФ (ДКНФ) можуть бути перетворені (не завжди) до виду, що містить менше число змінних і операцій в порівнянні з початковим. Таке перетворення називається мінімізацією.

Перетворення функції можна розділити на два етапи:

• на першому етапі здійснюється перехід від канонічної форми (ДДНФ або ДКНФ) до так званої скороченої форми;

• на другому етапі – перехід від скороченої форми до мінімальної форми.

На першому етапі, застосовуючи основні закони булевої алгебри, можна було б аналітично зменшити складність отриманого виразу ДДНФ.

Уявімо, що задана функція F представлена в ДДНФ. Для здійснення спрощення виконуються дві дії:

1. Операція склеювання;

2. Операція поглинання.

Операція склеювання зводиться до знаходження пар членів, відповідних виду wx або , і перетворенню їх в наступні вирази:

Результати склеювання w тепер грають роль додаткових членів.

Потім виконується операція поглинання. Вона заснована на рівності

(член w поглинає вираз wz). Унаслідок цієї дії з логічного виразу викреслюються всі члени, що поглинаються іншими змінними, результати яких отримані в операції склеювання. Обидві операції можуть виконаються до тих пір, поки це може бути здійсненно.

Приклад: Булева функція F(x₁, x₂, x₃) задана наведеною таблицею істинності.

x1	x2	x3	F(x1, x2, x3)
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

ДДНФ для цієї функції виглядає так:

Використовуючи властивість ідемпотентності до четвертого доданка, можна дописати ще один шостий член:

Склеюючи перший і четвертий члени, другий і третій та п’ятий і шостий отримаємо:

В отриманому виразі склеюючи другий і третій члени, будемо мати:

Подальше проведення операцій склеювання і поглинання виявляється неможливим. Таким чином отримана скорочена форма вираження заданої функції (в даному випадку вона збігається з мінімальною формою), яка значно простіша її початкової версії. Структурна схема реалізації отриманої функції матиме вид, представлений на рис. 4.9.

К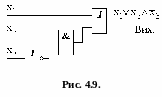 омпактною і дуже зручною формою запису логічної функції, що використовується поряд з таблицею істинності, є карта Карно¹. Карта Карно є спеціальною компактною формою таблиці істинності, яка дозволяє не лише представити функцію, але і подати її в скороченому виді. Кількість кліток в карті Карно дорівнює кількості рядків в таблиці істинності. Кожна клітка відповідає одному рядку таблиці. Комбінації вхідних змінних розподіляються по двох сторонах прямокутника, а відповідні значення функції в клітках таблиці, що знаходяться на перетині рядків, і стовпчиків, відповідних вибраним станам змінних. Розподіл комбінацій вхідних змінних по сторонах повинен бути таким, щоб різниця в двох сусідніх рядках або стовпчиках була не більше ніж в одному розряді.

Якщо потрібно отримати карту Карно для деякої функції, спочатку треба записати цю функцію в ДДНФ або у вигляді звичайної таблиці істинності. Кожен доданок булевого виразу в ДДНФ, або кожна одиниця в стовпчику функції вихідної таблиці істинності, задається на карті Карно одиницею у відповідній клітці. Координати цієї клітки містять ті ж вхідні змінні і їх інверсії, що і даний доданок ДДНФ булевого виразу (або даний рядок вихідної таблиці істинності).

Карти Карно можуть застосовуватися для функцій навіть від 8–12 змінних. Нижче наводяться карти Карно для кількості змінних 2, 3, 4, …, 6 (рис. 4.10, 4.11).

Метод Карно заснований на законі склеювання. Склеюються набори, що відрізняються один від одного лише значенням одного розряду. Такі набори називаються сусідніми, і вони відповідають сусіднім кліткам карти Карно. Зауважимо, що в картах Карно верхній рядок є сусіднім з нижнім, а правий стовпчик сусідній з лівим.

Якщо в карті Карно зустрічаються групи з 2-х, 4-х, 8-ми і т.д. сусідніх кліток, що містять одиниці, і які можна виділити контуром у вигляді квадрата або прямокутника², то така група може бути описана одним логічним добутком. Клітки можуть одночасно входити до складу кількох груп. У цей добуток входять лише змінні даної групи, значення яких для всіх вічок групи залишаються незмінними.

Рис. 4.10

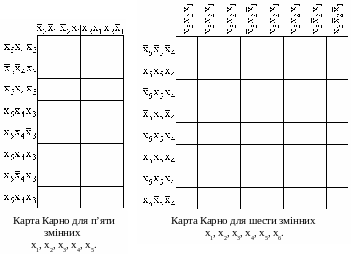
Рис. 4.11.

Виокремлені логічні добутки (кон’юнкції) об’єднуються через диз’юнкцію. В результаті скорочена функція є логічною сумою логічних добутків, відповідних окремим групам

Якщо потрібна КНФ, то розглядаються ті клітки які містять нулі.

Як приклад скорочення за допомогою карти Карно побудуємо скорочені ДНФ для логічних функцій, що визначають вихідні сигнали в однорозрядному суматорі. Скористуємось готовою таблицею істинності (табл. 4.4). Заповнимо клітки карти Карно для трьох змінних А_і, В_і, Р_і–1 для функції, що визначає суму S_i (рис. 4.12-а) і клітки такої ж карти для функції, що визначає перенос в старший розряд Р_i (рис. 4.12-б).

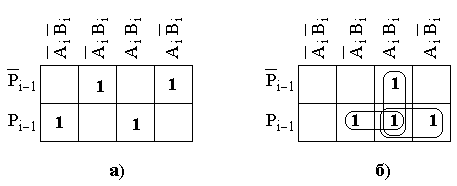
а) б)

Рис. 4.12.

На карті Карно для логічної функції, що визначає суму S_i неможливо виокремити прямокутники Карно, а отже, спростити наведену вище канонічну ДДНФ неможливо, вона такою ж і залишається:

На Карті Карно для логічної функції, що визначає перенос в старший розряд Р_i, виокремлені три прямокутника, кожний із двох кліток. В кон’юнкції, що відповідають прямокутникам входять тільки змінні, які в межах прямокутника не змінюють свого значення. Отже, отримуємо скорочену ДНФ, рівну отриманій вище канонічній ДДНФ:

На другому етапі здійснюється перехід від скороченої форми до мінімальної форми. Як і на першому етапі, в отриманих логічних виразах можуть міститися члени, усунення яких жодним чином не вплине на кінцевий результат. Отже, наступний етап мінімізації – вилучення таких змінних. Кінцевий вираз досягається за рахунок повторного використання операцій склеювання і поглинання.

Для отриманих на першому етапі скорочених форм ДНФ у прикладі розглянутого двійкового суматора ці операції здійснити не вдасться, що свідчить про те, що отримані скорочені форми збігаються із мінімальними.

Н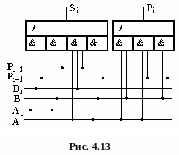 а основі отриманих виразів можна скласти схему пристрою, що реалізовує задані функції. Структурна схема реалізації зазначених функцій наводиться на рис. 4.13.