Релейно-контактные схемы

Основными элементами релейно-контактных схем являются электромагнитные реле с замыкающими контактами. В качестве логических переменных в схемах используют изменения состоя ний контактов релейных элементов. При этом логические переменные обозначают строчными буквами (например, у₁ у₂ ..., у_n, x₁, х₂ ..., х_n), а устройства — прописными, причем устройства, формирующие выходные сигналы, обозначают У₁ У₂ ..., У_п, а устройства, предназначенные для передачи входных и промежуточных сигналов, — Х₁ Х₂ ..., Х_п. Постоянно замкнутым контактам в электрической цепи соответствует цифра 1, а постоянно разомкнутым — 0.

Операция И реализуется группой последовательно соединенных контактов управляющих реле Х₁ Х₂ ..., Х_п в цепи обмотки реле У, а операция ИЛИ — группой параллельно соединенных контактов.

Допустим, что необходимо получить сигнал на выходе логического устройства только в случае, если на его вход будут одновременно поданы два входных сигнала. Эта описанная словесно ситуация соответствует логической операции И с двумя переменными. Для ее технической реализации на релейно-контактных элементах необходимо обеспечить срабатывание электромагнитного реле У, для чего сигналы (напряжения) подаются на обмотки двух реле Х₁ Х₂ соответствующие контакты х₁ х₂ которых включены последовательно с обмоткой реле У. При замыкании обоих контактов напряжение подается на обмотку реле У. Выходной сигнал у появляется при замыкании контакта у.

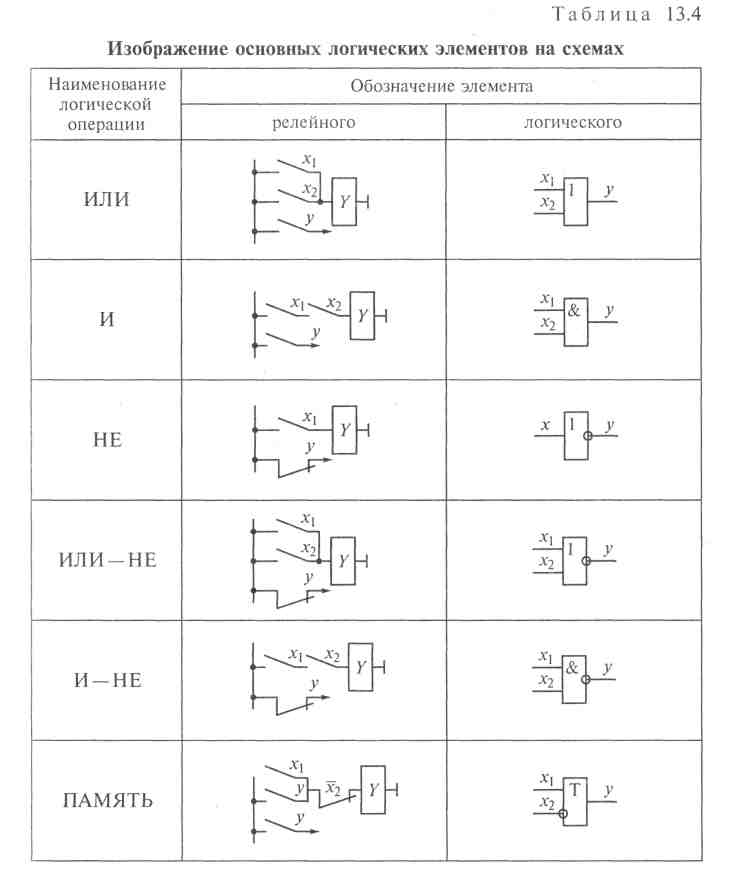
Релейный эквивалент логический операции И см. в табл. 13.4.

Изображение основных логических элементов на схемах

Первые устройства, для описания действий которых использовались логические функции, выполнялись на релейно-контактных элементах. Затем появились бесконтактные устройства, предназначенные только для логических преобразований сигналов и представляющие собой конструктивно оформленные изделия.

Устройства автоматики, действия которых описываются элементарными логическими функциями, называют обычно в соответствии с реализуемыми ими логическими операциями элементами НЕ, И, ИЛИ, И —НЕ, ИЛИ —НЕ. Их обозначения на схемах показаны в табл. 13.4.

Минимизация логических функций

Имея необходимые элементы, по логической функции можно синтезировать логическое устройство любой сложности. Однако схема такого устройства может оказаться неоправданно сложной, требующей использования большого числа логических элементов, что соответственно будет влиять на его стоимость и надежность. Во многих случаях можно упростить логическую функцию так,

чтобы соответствующая ей схема устройства также существенно упростилась, выполняя при этом поставленную задачу.

Методы такого упрощения называются методами минимизации логических функций. Основными из них являются метод непосредственного упрощения, применяемый при числе переменных, не превышающем трех, а также метод Квайна и карты Вейча, используемые при числе переменных не более пяти. Все эти методы подробно рассмотрены в специализированной литературе.

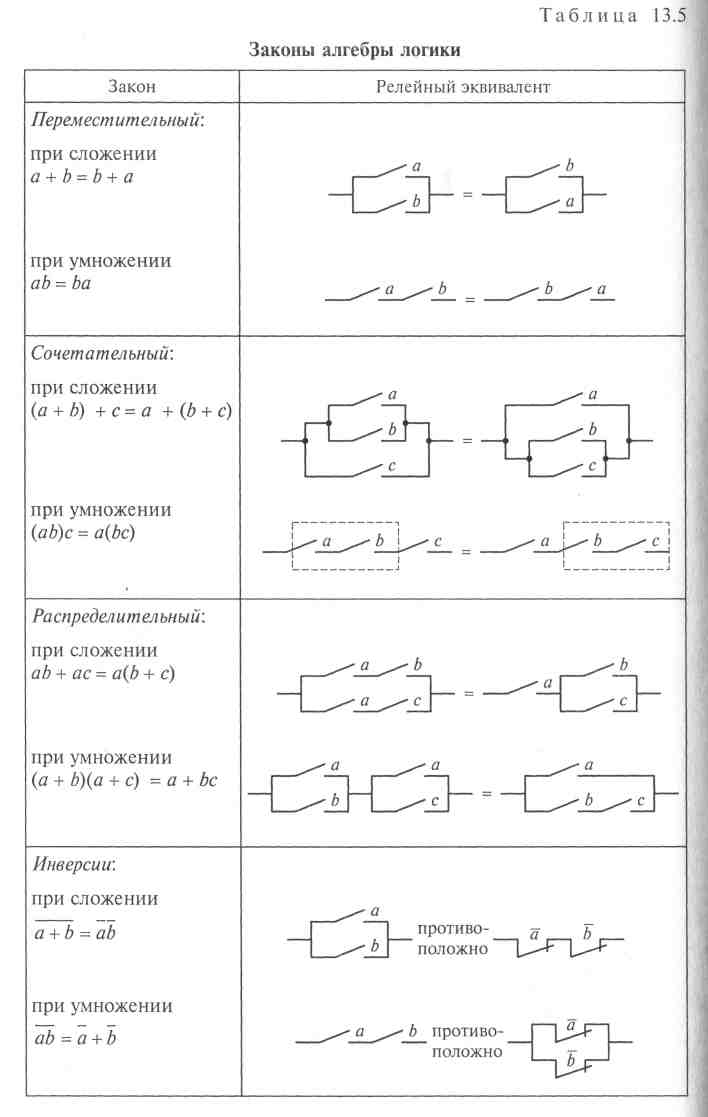
Минимизация основана на применении законов алгебры логики, которые приведены в табл. 13.5 для минимального числа переменных. Эквивалентность левой и правой частей уравнений обозначается в них знаком равенства. Рядом изображены их релейные эквиваленты.

Инверсия произвольной комбинации двоичных переменных, соединенных знаками «плюс» или «умножение», эквивалентна замене в этой комбинации значений переменных их инверсиями при одновременном изменении знака «плюс» на знак «умножение», и наоборот. Например,

Таким образом, закон инверсии позволяет заменить операцию ИЛИ операцией И, а при необходимости и наоборот. Это очень важно, поскольку при широком применении интегральных логических элементов в построении логических устройств наиболее часто используют элементы И—НЕ, ИЛИ—НЕ.

Преобразование логических функций с применением распределительного закона является основным методом упрощений, так как вынесение общего множителя за скобки сокращает общее число переменных в выражении, а следовательно, позволяет сократить число элементов в схемах логических устройств.

Преобразование функций в целях упрощения называют минимизацией логических функций.

Выполняя минимизацию, используют также следствия законов алгебры логики, основными из которых являются:

Процесс упрощения логических функций в целях их минимизации при прямом использовании законов и следствий алгебры логики может быть пояснен следующим примером.

Пример. Требуется минимизировать логическую функцию

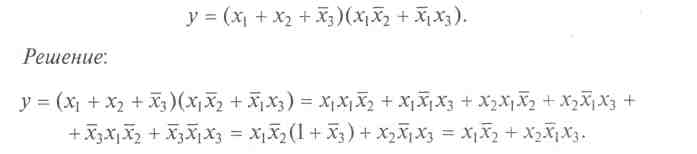
Наборы логических элементов, позволяющие реализовать логические функции любой сложности, называют базисами.

Имея только логические элементы НЕ, И, ИЛИ, можно реализовать логические алгоритмы любой сложности. Именно в этом базисе ранее изготовляли полупроводниковые логические устройства.

Базис для построения логических устройств может состоять из одного вида логических элементов, если в качестве базового выбрать, например, элемент И—НЕ или элемент ИЛИ—НЕ.

С появлением интегральных технологий производства электронных компонентов стали изготовлять логические устройства в базисе одного из этих типов элементов. Для реализации алгоритма одинаковой сложности в базисах И—НЕ, ИЛИ—НЕ формально требуется большее число элементов, чем в базисах НЕ, И, ИЛИ. Но для интегральных электронных схем, где десятки тысяч элементов можно разместить на одном кристалле, это несущественно. Например, чтобы реализовать в базисе И—НЕ логическую операцию ИЛИ, требуется три элемента.

По типам интегральных схем различают элементы резистивно-транзисторной логики (РТЛ), диодно-транзисторной логики (ДТЛ), транзисторно-транзисторной логики (ТТЛ), эмиттерно-связанной логики (ЭСЛ), логики с инжекционным питанием (И²Л), на МОП-транзисторах, в том числе с дополняющими типами проводимости (КМОП) и др.