12.6. Критерии устойчивости сау Алгебраический критерий устойчивости Рауса-Гурвица

В этом случае исходным при анализе замкнутой САУ на устойчивость является характеристическое уравнение замкнутой САУ:

По критерию Рауса-Гурвица необходимым условием устойчивости замкнутой САУ (в которой все действительные корни характеристического уравнения отрицательные, а у комплексных корней — отрицательная действительная часть) являются положительные коэффициенты а_п...а₁ и свободный член а₀ исходного характеристического уравнения. Это условие является также достаточным для систем с характеристическим уравнением 1 и 2-го порядков. Естественно, при п = 1 характеристическое уравнение имеет вид

a₁p + a₀ = 0,

т.е если a₁ > 0 и a₀ > 0, то корень р < 0, и САУ устойчивая.

При п = 2 уравнение имеет вид

В этом случае, если а₁² < 4а₂а₀, корни могут быть комплексные, но действительная их часть всегда будет отрицательной, если а₂ , а₁ , а₀ > 0.

Для систем выше второго порядка при сохранении необходимого условия устойчивости а_п... а₀ > 0 достаточным условием будут положительные знаки определителей Гурвица, т.е. главного определителя матрицы и ее диагональных миноров, которые составляются по определенному правилу из коэффициентов а_п...а₁ и свободного члена а₀ характеристического уравнения замкнутой САУ.

Для системы третьего порядка с характеристическим уравнением

определитель такой матрицы

При этом если Δ₁> 0, то САУ устойчивая.

Для системы четвертого порядка с характеристическим уравнением

должен быть положительным главный определитель Гурвица

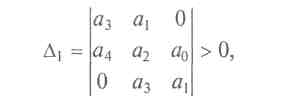
а также определитель диагонального минора:

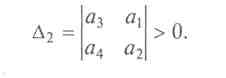
Следовательно,

Данный алгебраический критерий устойчивости для систем выше пятого порядка, как правило, не применяется, поскольку тогда вычисление определителей Гурвица становится сложной задачей. Для таких систем можно применить частотные критерии устойчивости Михайлова и Найквиста.

Частотный критерий устойчивости Михайлова

Исходным при анализе замкнутой системы на устойчивость по критерию А. В. Михайлова (русский математик, разработавший этот критерий в 1930 г.) также является характеристическое уравнение замкнутой САУ:

Заменив в этом уравнении оператор Лапласа р на выражение iω в соответствующей степени, получают аналитическое выражение вектора Михайлова, который делят на действительную и мнимую части:

Далее строят годограф вектора Михайлова — кривую, которая описывает конец этого вектора на комплексной плоскости при изменении частоты ω от 0 до ∞.

Определение: замкнутая система будет устойчивой, если годограф вектора Михайлова (при ω = 0), начиная свое движение с положительной действительной полуоси комплексной плоскости (а₀ > 0),

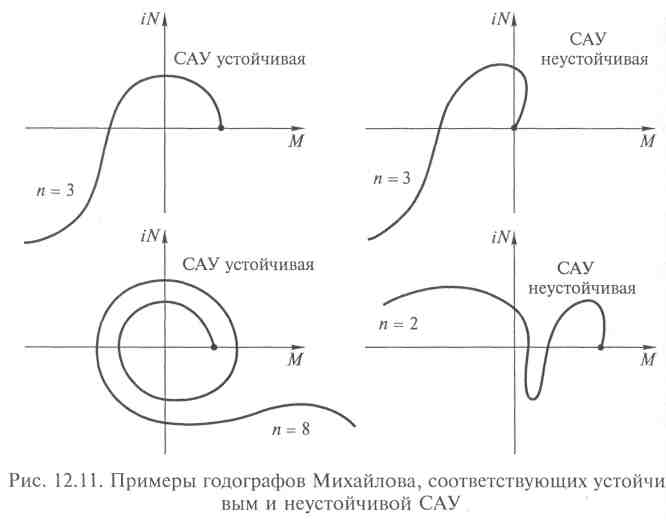
двигаясь против часовой стрелки и нигде не обращаясь в нуль, последовательно обходит столько квадрантов комплексной плоскости, каков порядок исходного характеристического уравнения замкнутой системы, и уходит в последнем квадранте в бесконечность.

На рис. 12.11 даны примеры годографов Михайлова, соответствующих устойчивым и неустойчивым САУ.

Критерий устойчивости Михайлова удобно применять для систем высокого порядка, т.е. с п = 6, 8, 10. При делении аналитического выражения вектора Михайлова на действительную и мнимую части в первую — попадают члены с четной степенью, так как i²= -1, i⁴ = +1, i⁶ = -1, а в последнюю — с нечетной, так как i¹ = i, i³ = -i, i⁵ = i. При построении годографа Михайлова, задавая значения со < 1, можно учитывать члены с низкими степенями, а задавая значения ω > 1, — с высокими.