9.3. Астатическое (интегрирующее) звено

Типовое дифференциальное уравнение этого звена имеет вид

Это уравнение можно решить в общем виде, взяв интегралы левой и правой его частей:

Посредством преобразования Лапласа получаем передаточную функцию астатического звена.

Операторная форма записи дифференциального уравнения

Передаточная функция имеет вид

Из передаточной функции легко получить аналитическое выражение вектора АФХ астатического звена путем замены оператора Лапласа р на выражение /со:

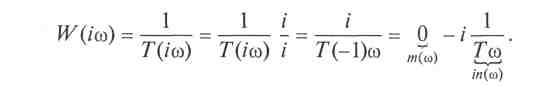
Разделив после преобразования вектор АФХ на действительную т и мнимую т части, легко построить его годограф, изменяя частоту ω от 0 до ∞ (рис. 9.8).

Конец вектора АФХ перемещается по отрицательной мнимой полуоси комплексной плоскости, которая и будет графиком АФХ для астатического звена.

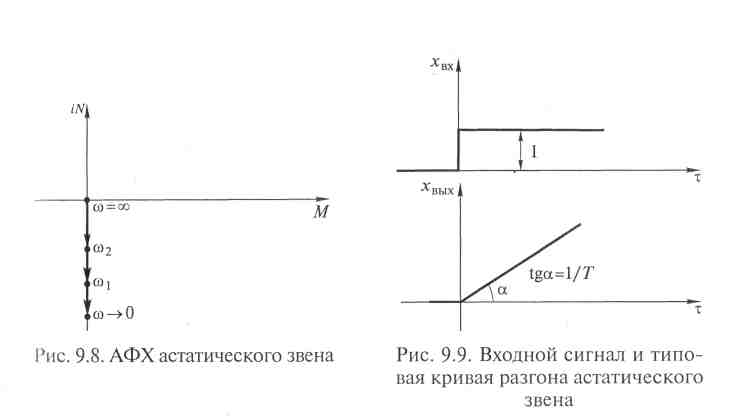
На рис. 9.9 изображена типовая кривая разгона астатического звена. По этому графику видно, что объект, аппроксимируемый астатическим ТДЗ, не обладает свойством самовыравнивания.

По кривой разгона легко определить коэффициент T в передаточной функции астатического звена:

В литературе передаточную функцию астатического звена иногда записывают в виде

а после преобразования

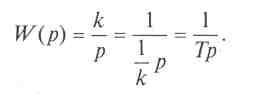
Примером реализации астатического ТДЗ является любой бункер-накопитель в технологической цепи машиностроительного производства.

Также примером реализации астатического ТДЗ может быть цилиндрический бак, из которого вода откачивается насосом постоянной производительности (рис. 9.10).

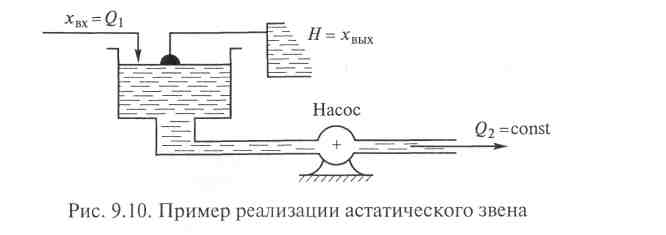
Равновесие в этой системе наступает только при равенстве входного потока Q₁ производительности насоса Q₂. В остальных случаях будет непрерывное наполнение или опорожнение бака в соответствии с кривой разгона типового астатического звена.

Объекты, которые аппроксимируются астатическим (интегрирующим) звеном, называют астатическими. Такие объекты не обладают свойством самовыравнивания.

9.4. Колебательное (апериодическое 2-го порядка) звено

Типовое дифференциальное уравнение этого звена имеет вид

Формально заменив d²/dτ² на p², а d/dτ на р, получим операторную форму записи этого дифференциального уравнения, преобразованного по Лапласу в алгебраическое:

Поскольку это уравнение алгебраическое, можно х_вых(р) вынести за скобки:

Преобразуя последнее уравнение в отношение выходного сигнала к входному, получим передаточную функцию колебательного звена:

Из передаточной функции можно получить аналитическое выражение вектора АФХ колебательного звена, заменив оператор Лапласа р на выражение iω:

Чтобы выделить действительную и мнимую части в выражении вектора АФХ, проведем следующие алгебраические преобразования:

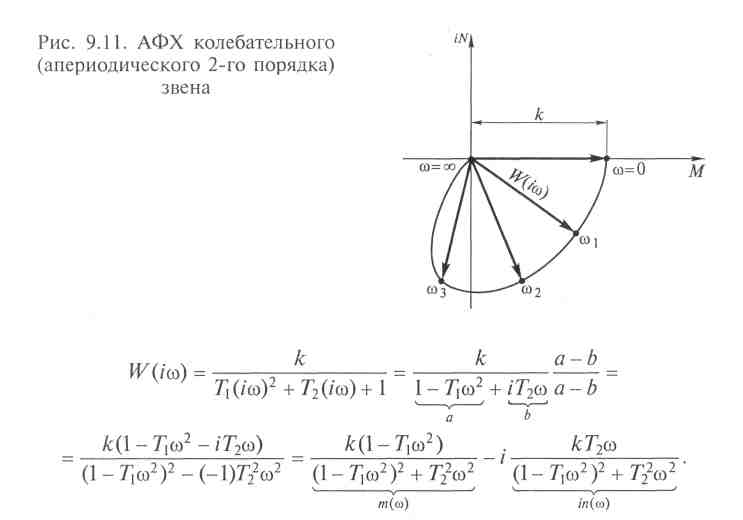
Изменяя частоту от 0 до ∞ в действительной m(ω) и мнимой in(ω) частях вектора АФХ данного звена, легко построить его годограф (рис. 9.11).

Типовые кривые разгона колебательного и апериодического 2-го порядка звеньев приведены на рис. 9.12. Различие приведенных кривых определяет соотношение коэффициентов Т₁ и Т₂ в исходном типовом дифференциальном уравнении: если Т₂² < 4T₁, то система ведет себя как колебательное звено, если же Т₂² ≥ 4T₁— как апериодическое звено 2-го порядка.

Из рис. 9.12 очевидно, что объекты, аппроксимируемые колебательным или апериодическим 2-го порядка звеном обладают свойством самовыравнивания, т.е. способностью самостоятельно восстанавливать состояние равновесия после возмущающего воздействия.

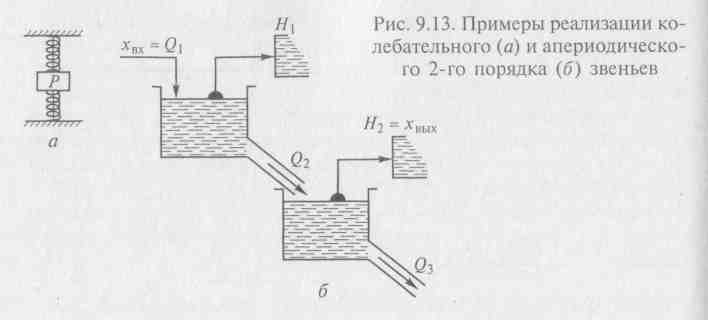
Примером реализации колебательного звена может служить механическая система (колесная пара вагона), изображенная на рис. 9.13, я, а апериодического звена 2-го порядка — система из двух проточных прудов (рис. 9.13, б), в которой регулируемым параметром х_вых является уровень Н₂ воды во втором пруду.

По кривым разгона колебательного и апериодического звеньев легко найти значение коэффициента k в их передаточной функции. Определить же коэффициенты Т₁ и Т₂ значительно сложнее.