5. Диаграммы Эйлера-Венна

Диаграммы Эйлера-Венна помогают наглядно проиллюстрировать многие соотношения между множествами. На рисунке 32 показано применение диаграмм Эйлера-Венна для наглядного изображения основных операций над множествами.

^{U U} U

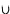
A ^{A B} A B

A A B A B

U U ^U

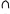
^A A B A B

A A B A B

Рисунок 4: Использование диаграмм Эйлера-Венна для иллюстрации основных операций над множествами

6. Прямое произведение множеств

Пусть A = {a₁, a₂, ..., a_k}, B = {b₁, b₂, ..., b_l}

A × B = {(a₁, b₁), (a₁, b₂), ..., (a₁, b_l), (a₂, b₁), ..., (a_k, b_l)} =

= {(a, b) | a ∈ A, b ∈ B}

• прямое (декартово) произведение множеств A и B.

Во многих случаях порядок проведения операций произведения не важен. Тогда считают, что

A × (B × C) = (A × B) × C = {(a, b, c) | a ∈ A, b ∈ B, c ∈ C}.

Аналогично определяется прямое произведение любого конечного числа множеств.

A₁ × A₂ × ... × A_t = {(a₁, a₂, ..., a_t) | a_i ∈ A_i, i = 1, t}

Если речь будет идти о прямом произведении множества на себя, то будем заменять запись нескольких множеств, на знак степени:

A × A × ... × A = A^t.

t

4. Бинарные отношения и функции

1. Бинарные отношения

Определение 1.4.1 . Бинарным (двуместным) отношением ρ

называется множество упорядоченных пар. Если некоторая пара (x, y)

принадлежит отношению ρ пишут (x, y) ∈ ρ или xρy.

Замечание 1.4.1 . n-арным отношением называют множество упорядоченных n-ок. Любое множество можно назвать унарным отношением.

Областью определения бинарного отношения ρ называется множество

D_ρ = {x | существует такое y, что xρy}.

Областью значений бинарного отношения ρ называется множество

R_ρ = {y | существует такое x, что xρy}

Пример 1.4.1 . 1) ρ = {(1, 2), (2, 3), (1, 5), (3, 3)}. Тогда D_ρ = {1, 2, 3},

R_ρ = {2, 3, 5}.

2. {(x, x) | x - вещественное число}. Тогда D_ρ = R_ρ = R.

3. {(x, y) | x, y - целые числа и найдется такое целое число z, что

x + z = y}. Тогда D_ρ = R_ρ = Z.

Каждое бинарное отношение является подмножеством прямого произведения множеств X и Y таких, что D_ρ ⊆ X и R_ρ ⊆ Y .

Обратным отношением для отношения ρ называют отношение

ρ⁻¹ = {(x, y) | (y, x) ∈ ρ}.

Композицией отношений ρ₁ и ρ₂ называется отношение

ρ₂ ◦ ρ₁ = {(x, z) | существует такое y, что xρ₁y и yρ₂z}.

Утверждение 1.4.1 . Для любых бинарных отношений ρ, ρ₁, ρ₂

выполняются следующие свойства: 1) (ρ⁻¹)⁻¹ = ρ;

2) (ρ₂ ◦ ρ₁)⁻¹ = ρ⁻¹ ◦ ρ⁻¹

1 2

Доказательство. Пункт 1 непосредственно следует из определения обратного отношения. Покажем истинность пункта 2:

(ρ₂ ◦ ρ₁)⁻¹ = {(z, x) | ∃y : xρ₁y, yρ₂z} =

= {(z, x) | ∃y : yρ⁻¹x, zρ⁻¹y} = ρ⁻¹ ◦ ρ⁻¹

1 2 1 2

D

2. Функции

Определение 1.4.2 . Бинарное отношение f называется функцией, если из (x, y) ∈ f и (x, z) ∈ f следует, что y = z.

Две функции равны, если они состоят из одних и тех же элементов (как и любые множества).

Иногда приходится сталкиваться с трудностями в определении области значений функций. Тогда, если D_f = X и R_f ⊆ Y , то говорят,

что функция f задана на множестве X со значениями в множестве Y

(осуществляет отображение множества X во множество Y ), и пишут

f : X → Y .

Если f - функция, вместо (x, y) ∈ f пишут f (x) = y и говорят, что y

• значение соответствующее аргументу x (образ элемента x). x называют

прообразом элемента y.

Пример 1.4.2 . 1) {(1, 2), (2, 3), (48, *), (D, D)} - функция;

2) {(1, 2), (1, 3), (2, 4)} - не функция;

3) ρ{(x, x² + 2x + 1) | x - вещественное число} - функция y = x² +

2x + 1. Обратное бинарное отношение ρ⁻¹ в этом случае функцией не

является.

Пусть f : X → Y .

Определение 1.4.3 . Функцию (отображение) f назовем инъектив- ной фукнцией (инъекцией), если для любых x₁, x₂ ∈ X и любого y ∈ Y из

y = f (x₁) и y = f (x₂) следует, что x₁ = x₂.

Определение 1.4.4 . Функция f называется сюръективной функцией (сюрьекцией), если для любого элемента y ∈ Y существует элемент x ∈ X такой, что y = f (x).

Определение 1.4.5 . Функция f называется биективной функцией (биекцией), если она и сюръективна, и инъективна.

Если указана биективная функция f : X → Y , говорят. что осуществляется взаимнооднозначное соответствие между множествами X и Y .

Пример 1.4.3 . Рассмотрим функции f : R → R.

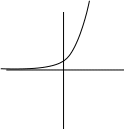
1. f (x) = e^x инъективна, но не сюръективна (рис. 5-a));

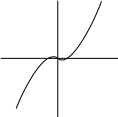
2. f (x) = x³ − x сюръективна, но не инъективна (рис. 5-b));

3. f (x) = 2x + 1 биективна.

1. y=ex

2. y=x³-x

Рисунок 5: Примеры функций

Утверждение 1.4.2 . Композиция двух функций есть функция. При этом, если f : X → Y и g : Y → Z, то g ◦ f : X → Z.

Доказательство. Пусть (x, z₁) ∈ g ◦f и (x, z₂) ∈ g ◦f . Тогда существуют y₁ и y₂: z₁ = g(y₁) и z₂ = g(y₂). При этом y₁ = f (x) и y₂ = f (x). Поскольку, f - функция, то y₁ = y₂. Поскольку g - функция, то

z₁ = g(y₁) = g(y₂) = z₂. Таким образом, g ◦ f - функция.

Покажем, что g ◦ f : X → Z. Так как f : X → Y , для любого x ∈ X

существует y ∈ R_f ⊆ Y : f (x) = y. Так как g : Y → Z, существует

z ∈ R_g ⊆ Z: z = g(y) = g(f (x)) = (g ◦ f )(x). Таким образом, для любого x ∈ X мы нашли такой z ∈ Z, что (x, z) ∈ g◦f . Следовательно, D_g◦f = X. С другой стороны, R_g◦f ⊆ R_g ⊆ Z, что и требовалось доказать.

D

Утверждение 1.4.3 . Композиция двух биективных функций есть биективная функция.

Доказательство. Пусть, f : X → Y и g : Y → Z - биекции. Пусть, для некоторых x₁, x₂ ∈ X и z ∈ Z верно z = g ◦ f (x₁) и z = g ◦ f (x₂). Пусть, y₁, y₂ ∈ Y те элементы, для которых y₁ = f (x₁) и y₂ = f (x₂).

Тогда, z = g(y₁) = g(y₂). Поскольку g инъективна, y₁ = y₂ и, поскольку

f инъективна, x₁ = x₂. Следовательно, g ◦ f - инъективна.

Пусть z ∈ Z. Тогда, поскольку g сюрьективна, существует y ∈ Y :

g(y) = z. Поскольку f сюрьективна, существует x ∈ X: f (x) = y.

Следовательно, g ◦ f (x) = z и g ◦ f сюрьективна. Таким образом, g ◦ f -

биекция.

D

Пусть f ⁻¹ - отношение обратное к f . Если f ⁻¹ осуществляет

отображение множества Y во множество X, говорят, что f ⁻¹ - обратное

отображение.

Утверждение 1.4.4 . Отображение f : X → Y имеет обратное отображение f ⁻¹ : Y → X тогда и только тогда, когда f - биекция. При этом f ⁻¹ тоже будет биекцией.

Доказательство. Достаточность. Пусть, (y, x₁) ∈ f ⁻¹ и (y, x₂) ∈ f ⁻¹. Тогда, f (x₁) = f (x₂) = y. Из инъективности функции f следует, что

x₁ = x₂ и, следовательно, f ⁻¹ - функция.

Из сюръективности функции f следует, что для любого y ∈ Y

существует x ∈ X: f (x) = y. Другими словами, для любого y ∈ Y

существует x ∈ X: f ⁻¹(y) = x. Следовательно, D_f ⁻¹ = Y и f ⁻¹

осуществляет отображение из Y в X.

Покажем, что f ⁻¹ - биекция. Поскольку f определена на всем множестве X, f ⁻¹ - сюрьекция. Пусть существуют такие y₁, y₂ ∈ Y и x ∈ X, что x = f ⁻¹(y₁) = f ⁻¹(y₂). Тогда, (x, y₁) ∈ f и (x, y₂) ∈ f и, поскольку f функция, y₁ = y₂. Следовательно, f ⁻¹ - инъекция.

Необходимость доказывается из тех же соображений, рассмотренных в обратном порядке: если f ⁻¹ функция, то f - инъективна; если f ⁻¹

осуществляет отображение из Y в X, f - сюръективна.

D

Замечание 1.4.2 . Чтобы обратное отношение f ⁻¹ было функцией, достаточно инъективности f .

Тождественным отображением множества X на себя называется отображение e_X : X → X такое, что для любого x ∈ X верно e_X (x) = x. Если f : X → Y тогда верно, что e_Y ◦ f = f и f ◦ e_X = f .

Утверждение 1.4.5 . Если f : X → Y - биекция, то 1) (f ⁻¹ ◦ f ) = e_X ;

2) (f ◦ f ⁻¹) = e_Y .

Доказательство. Для любого x ∈ X, (f ⁻¹ ◦ f )(x) = f ⁻¹(f (x)) = x. Для любого y ∈ Y , (f ◦ f ⁻¹)(y) = f (f ⁻¹(y)) = y.

D