6. Полином Жегалкина

Рассмотрим еще одно представление функции в виде формулы заданного вида.

Определение 2.1.13 . Формула вида

α₀ ⊕ α₁x₁ ⊕ α₂x₂ ⊕ ... ⊕ α_nx_n ⊕ α₁₂x₁x₂ ⊕ ... ⊕ α_12...nx₁x₂...x_n, (30)

где x₁, ..., x_n - логические переменные, а α₀, α₁, ..., α_12...n - логические константы, называется полиномом Жегалкина.

Замечание 2.1.9 . Для удобства будем также использовать следующую запись:

Пример 2.1.12 .

�

I⊆{1,...,n}

α(I) x_i.

i∈I

1 ⊕ X1 ⊕ x2x3 - полином Жегалкина.

Здесь n = 3, α₀ = α₁ = α₂₃ = 1, а α₂ = α₃ = α₁₂ = α₁₃ = α₁₂₃ = 0.

Утверждение 2.1.6 . Пусть f (x₁, ..., x_n) ∈ P₂. Тогда функция f может быть представлена полиномом Жегалкина, причем единственным образом.

Доказательство. Для начала докажем существование такого представления для функции. Прежде всего заметим, что произвольная

функция представима в виде формулы U₁ над {¬, ∨, ∧}: если f /= 0, ее

можно представить в виде СДНФ, а f = 0 представим как f = x ∧ x.

Воспользуемся законом де Моргана x ∨ y = x ∧ y и заменим все

дизъюнкции в формуле U₁ на конъюнкции и отрицание. Получим

представление функции f (x₁, ..., x_n) в виде формулы U₂ над системой

элементарных функций {¬, ∧}. Заменим в формуле U₂ все отрицания

на сложение по модулю два согласно тождеству x = 1 ⊕ x. Раскроем

все скобки, пользуясь дистрибутивностью ∧ относительно ⊕, и получим

формулу вида (30).

Теперь докажем единственность. Пусть

f (x₁, ..., x_n) = ^�

α(I) x_i = ^�

β(I) x_i.

I⊆{1,...,n}

i∈I

I⊆{1,...,n}

i∈I

• два различных полинома Жегалкина для функции f . Полиномы различны, когда отличаются наборы их коэффициентов α и β.

Выберем I^∗ ⊆ {1, ..., n} такой, что α(I^∗) /= β(I^∗) и α(I) = β(I)

для любого I ⊂ I^∗. Мы можем выбрать такой набор, начав с I₀ =

{1, ..., n} и последовательно удаляя индексы, если указанное свойство

не выполняется. Так, если для набора индексов I_k существует I ⊂ I_k:

α(I) /= β(I), то выбираем I_k+1 = I и так далее, пока не получим I_l с

искомыми свойствами.

Пусть

Тогда

σ_i =

⁽ 1, i ∈ I^∗, _{i = 1, n.}

0, i ∈/ I^∗,

f (σ₁, ..., σ_n) = ^�

α(I) σ_i = ^� α(I) = ^� α(I) ⊕ α(I^∗)

и в то же время

I⊆{1,...,n}

i∈I

I⊆I^∗

I⊂I^∗

f (σ₁, ..., σ_n) = ^�

β(I) σ_i = ^� β(I) = ^� β(I) ⊕ β(I^∗).

Таким образом,

I⊆{1,...,n}

i∈I

I⊆I^∗

I⊂I^∗

^� α(I) ⊕ α(I^∗) = ^� β(I) ⊕ β(I^∗) =⇒ α(I^∗) = β(I^∗).

I⊂I^∗

I⊂I^∗

Противоречие с нашим исходным предположением о I^∗ доказывает утверждение.

D

Замечание 2.1.10 . Полином Жегалкина является формулой над

{0, 1, ∧, ⊕}. 0 нам требуется для задания тождественно нулевой

функции. Для остальных случаев нам будет достаточно функций

1, ∧, ⊕.

Пример 2.1.13 . Рассмотрим функцию f , заданную формулой

f (x, y, z) = xy ⊃ z ∨ xy. Представим ее с помощью формулы над {¬, ∧}.

xy ⊃ z = xy ∨ z = xy ∧ z,

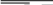xy ⊃ z ∨ xy = (xy ⊃ z) ∧ xy = xy ∧ z ∧ xy

Теперь избавимся от отрицаний и раскроем скобки.

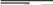xy ∧ z ∧ xy = 1 ⊕ ((1 ⊕ (xy ∧ (1 ⊕ z))) ∧ (1 ⊕ xy)) =

= 1 ⊕ 1 ⊕ xy ⊕ (xy ∧ (1 ⊕ z)) ⊕ (xy ∧ (1 ⊕ z))xy =

= xy ⊕ (xy ∧ (1 ⊕ z)) ⊕ (xy ∧ (1 ⊕ z)) = xy.

Таким образом, единственным ненулевым коэффициентом полинома Жегалкина для функции f оказался α₁₂ и сам полином имеет вид f (x, y, z) = xy.

Замечание 2.1.11 . Для построения полинома Жегалкина есть и более удобный способ - метод неопределенных коэффициентов. Предположим, что функция f (x₁, ..., x_n) задана таблицей значений для всех наборов аргументов. Нам известен общий вид полинома Жегалкина для f

�

I⊆{1,...,n}

α(I) x_i

i∈I

и требуется только вычислить коэффициенты α(I).

Проходя по всей таблице значений для f будем приравнивать общий вид полинома и известное значение функции на данном наборе, тем самым последовательно вычисляя коэффициенты α.

I 1,...,n

f (0, ..., 0) =

⊆{ }

α(I) ^1\

i∈I

0 = α(∅). Отсюда имеем первый

коэффициент:

α(∅) = f (0, ..., 0).

f (0, .., 0, 1) = α(∅) ⊕ α({n}) ∧ 1. Таким образом,

α({n}) = f (0, ..., 0, 1) ⊕ α(∅) = f (0, ..., 0, 1) ⊕ f (0, ..., 0, 0).

f (0, ..., 0, 1, 0) = α(∅) ⊕ α({n − 1}) ∧ 1 и

α({n − 1}) = f (0, ..., 0, 1, 0) ⊕ α(∅) = f (0, ..., 0, 1, 0) ⊕ f (0, ..., 0, 0, 0).

f (0, ..., 0, 1, 1) = α(∅) ⊕ α({n − 1}) ⊕ α({n}) ⊕ α({n − 1, n}) и,

следовательно,

α({n − 1, n}) = f (0, ..., 0, 1, 1) ⊕ α(∅) ⊕ α({n − 1}) ⊕ α({n}) =

= f (0, ..., 0, 1, 1) ⊕ f (0, ..., 0, 0, 0) ⊕ f (0, ..., 0, 1, 0)⊕

⊕f (0, ..., 0, 0, 0) ⊕ f (0, ..., 0, 1) ⊕ f (0, ..., 0, 0) =

= f (0, ..., 0, 1, 1) ⊕ f (0, ..., 0, 1, 0) ⊕ f (0, ..., 0, 0, 1) ⊕ f (0, ..., 0, 0, 0)

Продолжая этот процесс мы сможем вычислить все коэффициенты и тем самым получим полином Жегалкина для функции f .

Пример 2.1.14 . Построим полином Жегалкина для функции

f (x, y, z) = xy ⊃ z ∨ xy из примера 2.1.13 с помощью метода

неопределенных коэффициентов. В общем виде полином для функции

от трех переменных выглядит следующим образом:

f (x, y, z) = α₀ ⊕ α₁x ⊕ α₂y ⊕ α₃z ⊕ α_1,2xy ⊕ α_1,3xz ⊕ α_2,3yz ⊕ α_1,2,3xyz.

Переберем все возможные наборы аргументов.

f (0, 0, 0) = 0 = α0	⇒	α0 = 0,
f (0, 0, 1) = 0 = α0 ⊕ α3	⇒	α3 = 0,
f (0, 1, 0) = 0 = α0 ⊕ α2	⇒	α2 = 0,

f (0, 1, 1) = 0 = α₀ ⊕ α₂ ⊕ α₃ ⊕ α_2,3 ⇒ α_2,3 = 0,

f (1, 0, 0) = 0 = α₀ ⊕ α₁ ⇒ α₁ = 0,

f (1, 0, 1) = 0 = α0 ⊕ α1 ⊕ α3 ⊕ α1,3	⇒	α1,3 = 0,
f (1, 1, 0) = 1 = α0 ⊕ α1 ⊕ α2 ⊕ α1,2	⇒	α1,2 = 1,
f (1, 1, 1) = 1 = α0 ⊕ α1 ⊕ α2 ⊕ α3 ⊕ α1,2⊕
⊕α1,3 ⊕ α2,3 ⊕ α1,2,3	⇒	α1,2,3 = 0.

Полином Жегалкина имеет вид f (x, y, z) = xy, что совпадает с результатом примера 2.1.13.

Пример 2.1.15 . Рассмотрим еще один пример использования метода неопределенных коэффициентов. Пусть f (x, y, z) = (x ⊕ y) ⊃ z. Пусть

f (x, y, z) = xy ∨ xz ∨ yz.

f (0, 0, 0) = 0 = α0	⇒	α0 = 0,
f (0, 0, 1) = 0 = α0 ⊕ α3	⇒	α3 = 0,
f (0, 1, 0) = 0 = α0 ⊕ α2	⇒	α2 = 0,

f (0, 1, 1) = 1 = α₀ ⊕ α₂ ⊕ α₃ ⊕ α_2,3 ⇒ α_2,3 = 1,

f (1, 0, 0) = 0 = α₀ ⊕ α₁ ⇒ α₁ = 0,

f (1, 0, 1) = 1 = α0 ⊕ α1 ⊕ α3 ⊕ α1,3	⇒	α1,3 = 1,
f (1, 1, 0) = 1 = α0 ⊕ α1 ⊕ α2 ⊕ α1,2	⇒	α1,2 = 1,
f (1, 1, 1) = 1 = α0 ⊕ α1 ⊕ α2 ⊕ α3 ⊕ α1,2⊕
⊕α1,3 ⊕ α2,3 ⊕ α1,2,3	⇒	α1,2,3 = 0.

Следовательно, полином Жегалкина для функции f будет иметь вид

f (x, y, z) = xy ⊕ xz ⊕ yz.