2. Виды графов

Определение 4.1.7 . Псевдографом будем называть общий случай графа описанного в определении 4.1.1.

Определение 4.1.8 . Мультиграфом назовем граф, удовлетворяющий определению 4.1.1, который, дополнительно, не может содержать ребрер типа C (петель).

Псевдограф может содержать кратные ребра и петли. Мультиграф не может содержать петель, хотя может содержать любое количество кратных ребер. Пример псевдографа приведен на рисунке 34 a), пример мультиграфа - на рисунке 34 b).

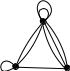
1. _{b) c) d)}

Рисунок 34: Псевдограф, мультиграф, обыкновенный граф и граф Бержа.

При необходимости можно говорить об ориентированных и неориентированных псевдографах и мультиграфах.

Приведем еще одно определение графа, которое, впрочем не является частным случаем определения 4.1.1.

Определение 4.1.9 . Гиперграфом назовем пару G = (V, E), где V

- конечное множество элементов произвольной природы, а E ⊂ 2^V -

произвольное множество подмножеств множества V .

Это самый широкий класс, включающий в себя все описанные выше классы неориентированных графов. Больше мы с ним не встретимся.

3. Обыкновенный граф

В самом простом случае, мы имеем дело с так называемыми обыкновенными графами (рис. 32). Такие графы не ориентированы (ребра не имеют направления, концевые вершины ребер равнозначны) и между любыми двумя вершинами может быть не более одного ребра; петель нет.

Таким образом в обыкновенный граф входят только ребра типа A (неориентированные ребра), причем не более одного ребра между любыми двумя вершинами.

Примеры обыкновенных гарфов приведены на рисунках 33 a), c), d) и рисунке 34 c). В большинстве случаев мы будем иметь дело именно с такими графами.

Обыкновенные графы удобно представлять в виде пары множеств

(V, E), где V - произвольное непустое множество (множество вершин графа), а E ⊆ V ⁽²⁾ = {{u, v} | u, v ∈ V ; u /= v} - множество

двухэлементных подмножеств множества V (множество ребер графа). Каждая пара {u, v} ∈ E соответствует ребру соединяющему вершины u

и v. Когда известно, что речь идет об обыкновенных графах, фигурные скобки часто заменяют на круглые для простоты записи и восприятия. Подразумвается, что пары тем не менее неупорядоченные ((u, v) = (v, u)).

Например, граф G на рисунке 33 является обыкновенным. Его множество вершин V = {1, 2, 3, 4, 5, 6} и множество ребер E =

{(1, 2), (1, 6), (2, 3), (2, 4), (3, 6), (4, 5), (5, 6)}.

Будем предполагать, что имеем дело с конечными графами: |V | < ∞.

Будем писать G = (V, E) для обозначения, что граф G имеет множество

вершин V и множество ребер E. Если нам понадобится указать, что некоторое множество является множеством вершин или ребер именно графа G, будем писать V (G) или E(G) соответственно.

Определение 4.1.10 . Порядком графа G называется число его вершин

- |V (G)|.

Определение 4.1.11 . Будем говорить, что вершины u и v смежны в графе G, если они соеденины ребром: (u, v) ∈ E(G). В этом случае u

и v называются концевыми вершинами ребра e = (u, v).

Определение 4.1.12 . Вершина v и ребро e называются инцидентными, если v является одной из концевых вершин e: e = (u, v).

Определение 4.1.13 . Два ребра e₁ и e₂ называются смежными, если у них есть общая концевая вершина: e₁ = (u, v), e₂ = (v, w).

Для удобства будем полагать, что G = (V, E), |V | = n, |E| = m. Будем называть такой граф, имеющий n вершин и m ребер (n, m)-графом.

Определение 4.1.14 . Степенью вершины v ∈ V в графе G назовем число deg_G v инцидентных ей ребер.

Вершина со степенью 0 называется изолированной. Вершина со степенью 1 называется висячей.

Определение 4.1.15 . Степенью графа ∆(G) называют максимальную из степеней вершин графа. Минимальную из степеней графа обозначают δ(G).

Определение 4.1.16 . Регулярным графом называется граф, у которого все вершины имеют одинаковую степень.

Теорема 4.1.1 . В обыкновенном графе число вершин нечетной степени четно.

Доказательство. Для графа с n вершинами и m ребрами имеет место

i=1

равенство ^):n

deg_G

v_i = 2m, где deg_G

v_i - степень i-той вершины.

D