2. Гамильтонов цикл

Определение 4.7.3 . Гамильтоновым циклом в графе G называется цикл, который проходит через все вершины графа ровно по одному разу.

Определение 4.7.4 . Граф G называется гамильтоновым графом, если в нем есть гамильтонов цикл.

Определение гамильтонова графа похоже на определение эйлерова графа, но здесь нет такого удобного критерия для определения, является ли граф гамильтоновым. Как мы покажем позже, проверка графов на гамильтоновость является N P -полной задачей.

8. Задачи и алгоритмы

1. Остов минимального веса

Задача 4.8.1 . Пусть имеется n населенных пунктов и между некоторыми из них проложены не асфальтированные дороги известной длины. Необходимо заасфальтировать часть дорог таким образом, чтобы была возможность проехать по новой дороге из любого пункта в любой другой, и при этом, чтобы суммарная длина заасфальтированных дорог была минимальной.

Сформулируем задачу на языке графов.

Задача 4.8.2 . Дан граф G = (V, E) и весовая функция W , сопоставляющая каждму ребру положительное значение:

W : E → R⁺.

Будем считать весом любого подграфа H графа G суммарный вес его ребер:

W (H) = ^\

e∈E(H)

W (e).

Требуется найти такой связный остовной подграф G₁ = (V, E₁), чтобы его вес W (G₁) был минимальным из весов всех остовных подграфов.

Очевидно, искомый подграф - дерево. С одной стороны он должен быть связен. С другой, если бы в нем имелся хотябы один цикл, мы смогли бы удалить любое ребро этого цикла и получить подграф, удовлетворяющий нашим требованиям, но меньшего веса.

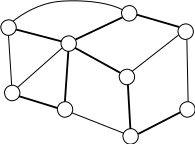
Пример минимального остовного дерева для взвешенного графа приведен на рисунке 45.

8

3 ₄

_{1 4} 5 ₄

2 ₆

₄ 5 5

_{4 7} 7

5 ₃

6 ₆ ⁵ ₅ 9

8

Рисунок 45: Остов миниального веса

Приведем алгоритм решения этой задачи.

Алгоритм 4.8.1 (Алгоритм Краскала).

Пусть G = (V, E), |V | = n, W : E → R₊.

1. e₁ = arg min_e∈E W (e).

2. i = 1; G_i = (V, E_i) = O_n + e₁.

3. while(i < n − 1){

e_i+1 = arg min

e∈E,

в G_i + e нет циклов

^Gi+1 ^{= G}i ^{+ e}i+1^; i = i + 1;

}

W (e);

На каждом шаге этого алгоритма мы выбираем самое "легкое" ребро графа, при добавлении которого у нас не образуется циклов вместе с уже выбранными ранее ребрами. Процесс завершается, когда мы выберем

n − 1 ребро. Чтобы убедиться, что этот алгоритм решает задачу об

остове минимального веса, нужно показать, что 1) мы действительно можем довести процесс до конца (всегда найдется такое n − 1 ребро);

2. построенный граф будет деревом; 3) это дерево будет минимальным по весу из всех остовных деревьев G.

Теорема 4.8.1 . Пусть граф G - связный граф. Тогда алгоритм Краскала строит минимальное остовное дерево.

Доказательство. 1) Во-первых, покажем, что агоритм всегда позволяет построить граф G_n−1.

Пусть на некотором шаге i (i < n−1) мы не смогли выбрать следующее

ребро e_i+1. Значит не существует ни одного такого ребра e ∈ E, что в

G_i + e нет циклов.

Граф G_i не имеет циклов по построению. Если бы граф G_i был связен, то по теореме 4.5.1 в нем было бы n − 1 ребро. Так как i < n − 1, граф

G_i не является связным.

Пусть H произвольная компонента связности графа G. Поскольку граф G связен, в нем существует ребро e = (u, v), соединяющее некоторую вершину u компоненты H с вершиной v, которая не принадлежит H.

По нашему предположению, G_i + e будет иметь цикл. Этот цикл должен проходить по ребру e (иначе цикл был бы и в графе G_i). Но тогда этот цикл состоит из маршрута между вершинами u и v и ребра (u, v). То есть в графе G_i должен быть маршрут между вершинами u и v и они обе принадлежать одной компоненте связности H ?!

2. Покажем, что построенный в алгоритме граф G_n−1 есть дерево.

Действительно, выбирая каждое ребро мы проверяем, что у нас не должно появляться циклов. Когда мы выберем n − 1 ребро, по теореме

4.5.1 они образуют связный граф без циклов - остовное дерево графа G.

2. Наконец докажем, что построено дерево минимального веса.

Пусть W_min(G) - вес минимального остовного дерева графа G. Пусть

S = {T | T = (V, E(T )) - остовное дерево грава G, W (T ) = W_min(G)}.

Пусть T ^∗ остовное дерево менимального веса, которое имеет наибольшее

число общих ребер с графом G_n−1:

T ^∗ = arg max |E(G_n−1) ∩ E(T )|.

T ∈S

Будем доказывать от противного. Пусть G_n−1 не является минимальным остовным деревом. Тогда T ^∗ не совпадает с G_n−1.

Пусть e_i - первое ребро в G_n−1, которого нет в T ^∗:

e_i = (u, v) ∈ E(G_n−1) : e_i ∈/ E(T ^∗), и ∀j < i ⇒ e_j ∈ E(T ^∗).

Рассмотрим граф T ^∗ + e_i. В нем обязательно есть цикл C, так как T ^∗ уже был связным графом - имел маршрут между вершинами u и v. Так как в графе G_n−1 нет циклов, в цикле C есть хотябы одно ребро e^t,

которого нет в G_n−1.

Рассмотрим граф T ^∗ + e_i − e^t. В этом графе нет циклов и он связен.

Значит T ^∗ + e_i − e^t остовное дерево. Вес T ^∗ + e_i − e^t не может быть меньше

веса минимального остовного дерева.

W (T ^∗) + W (e_i) − W (e^t) = W (T ^∗ + e_i − e^t) ≥ W (T ^∗). (D)

Следовательно

W (e_i) ≥ W (e^t). (∗)

Посмотрим с другой стороны. На i-том шаге алгоритма мы выбирали ребро e_i как ребро минимального веса из всех невыбранных ребер, не образующих циклов с ребрами e_j , j < i. Все ребра e_j , j < i входят и в

дерево T ^∗, а значит и ребро e^t не образует с ними цикла. Таким образом,

на i-том шаге алгоритма ребро e^t было кандидатом на выбор и было бы

выбрано, если бы W (e^t) < W (e_i). Следовательно

W (e_i) ≤ W (e^t). (∗∗)

Из неравенств (∗) и (∗∗) следует, что W (e_i) = W (e^t) и по формуле (D)

W (T ^∗ + e_i − e^t) = W (T ^∗) + W (e_i) − W (e^t) = W (T ^∗) = W_min(G).

То есть T ^∗ + e_i − e^t является остовным деревом минимального веса. При этом у графа T ^∗ + e_i − e^t на одно общее ребро с графом G_n−1 больше, чем у T ^∗, что противоречит выбору T ^∗.

Противоречие вызвано предположением, что G_n−1 не является деревом минимального веса. Следовательно G_n−1, полученный с помощью алгоритма Краскала, есть минимальное остовное дерево, что и требовалось доказать.

D

Замечание 4.8.1 . Заметим, что алгоритм Краскала является алгоритмом полиномиальной сложности. Не будем доказывать это строго. Для этого потребовалось бы определять, какие операции мы считаем элементарными, описывать алгоритм в терминах этих операций и подсчитывать их число в худшем случае в зависимости от размеров задачи. Рассмотрим лишь возможность выполнения за полиномиальное время основных действий алгоритма.

В основном цикле алгоритма ровно n − 1 шаг. Самым трудоемким

пунктом в этом цикле является выбор ребра, который можно

разделить на два основных действия:

1. Выбор ребра e минимального веса.

2. Проверка, появится ли цикл в графе после добавления ребра e.

1. Можно однократно стоставить список ребер, упорядоченных по весу (алгоритм сортировки имеет сложность порядка n · log n). Тогда будем

каждый раз брать самое легкое ребро и удалять его из списка. Всего за все итерации цикла мы в худшем случае переберем все ребра.

2. Пусть e = (u, v) - ребро под вопросом. Необходимо определить, появится ли в графе G_i + e цикл. Достаточно проверить, был ли в графе G_i маршрут между вершинами u и v.

Будем приписывать метки вершинам начиная с вершины u и далее

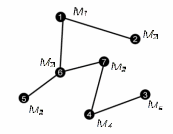
все смежные с уже помеченными вершинами. Остановимся, если смежных с помеченными непомеченных вершин больше нет (рис. 46). Максимум нам удастся пометить i + 1 вершину, так как больше соединено ребрами быть не может. По окончании процесса нам останется только проверить, есть ли метка у вершины v. Если есть, в графе G_i + e присутствовал бы цикл. Если нет, ребро e может быть выбрано в качестве e_i+1.

Итого, нам потребуется порядка n · log n действий, чтобы

отсортировать ребра, не более m действий выбора легких ребер, для

Рисунок 46: Проверка наличия маршрута между вершинами

каждого из которых нужно проверить наличие цикла, и порядка

const ·(n − 1) других действий

Замечание 4.8.2 . Этот алгоритм относится к так называемым жадным алгоритмам. Суть жадных алгоритмов состоит в том, чтобы на каждом шаге выбирать элемент с минимальным (или максимальным) значением некоторого параметра в итоге получая оптимальное решение.

Пример 4.8.1 . Легко убедиться, что жадный алгоритм применим не всегда. Например, рассмотрим задачу нахождения минимума суммы двух целых чисел с условием на значение их произведения.

x + y → min,

x · y = 30, x, y ∈ {2, 3, 5, 6, 10, 15}.

Очевидно, что решением этой задачи являются числа 5 и 6. В то же время следуя жадной стратегии мы должны были бы сначала выбрать самое маленькое значение x = 2, а затем подобрать наименьшее

значение для y, для которого выполняется условие x · y = 30 - y = 15.

Решение (2, 15) очевидно не является минимумом.

Жадный алгоритм здесь не дал правильного ответа.

9. N P -полные задачи теории графов