3. Теория алгоритмов

1. Машины Тьюринга

1. Понятие алгоритма

Интуитивно алгоритм можно рассматривать как последовательность действий, которая обладает рядом свойств.

1. Входные данные. Поскольку алгоритм решает некоторую общую задачу, он обычно получает некоторые инициирующие данные, в зависимости от которых выполняется.

2. Выходные данные. Любой алгоритм должен давать какой-то результат от своего выполнения.

3. Определенность. В каждый момент времени мы должны точно знать, какое действие выполнить следующим.

4. Элементарность. Это свойство значит, что каждый шаг алгоритма должен быть достататочно прост, чтобы его выполнение не требовало разбиения на меньшие шаги.

5. Конечность. Чтобы выдать результат алгоритм обычно должен завершить свою работу.

Для того, чтобы дать строго формальное определение алгоритма, введем понятие машины Тьюринга.

2. Машина Тьюринга

Определение 3.1.1 . Машиной Тьюринга называется совокупность пяти объектов < A, D, Q, q₁, I >:

1. Алфавит A = {a₁, ..., a_n} - множество символов данной машины

Тьюринга; |A| ≥ 1. Иногда алфавит называют множеством внешних

состояний машины Тьюринга.

2. Пустой символ D ∈/ A.

3. Множество состояний Q = {q₁, ..., q_k}, |Q| ≥ 1. В некоторых

случаях это множество также называют множеством внутренних

состояний машины Тьюринга.

4. Начальное состояние q₁ ∈ Q.

5. Программа I - множество команд вида q_ia → q_jb, где q_i, q_j ∈ Q,

a ∈ {D} ∪ A, b ∈ {D, L, R} ∪ A. Здесь L и R выделенные символы, такие

что L, R ∈/

{D} ∪ A. Кроме того, для любых q_i ∈ Q и a ∈ {D} ∪ A в

программе I может быть не больше одной команды q_ia → q_j b (иными

словами, в I нет двух команд с одинаковой левой частью).

Процесс функционирования машины Тьюринга. Машина Тьюринга (рис. 15) состоит из бесконечной в обе стороны ленты, разбитой на одинаковые ячейки, а также читающе-пишущей головки. В ячейках ленты могут быть записаны символы алфавита или пустой символ.

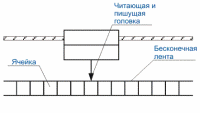
Рисунок 15: Машина Тьюринга

Работа машины Тьюринга понимается следующим образом (рис. 16). В начальный момент времени на ленте записано конечное слово α в

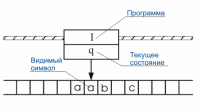
Рисунок 16: Функционирование машины Тьюринга.

алфавите A (или несколько слов разделенных пустым символом D) окруженное слева и справа бесконечным количеством пустых символов D; машина Тьюринга находится в состоянии q₁ и ее головка обозревает самую левую ячейку слова α. Пусть там записан символ a_i1 . В I ищется команда с q₁a_i1 в левой части. Если такая команда не найдется, машина

останавливается. Если команда найдется и это q₁a_i1 → q^ta_i^f , машина

переходит в состояние q^t и выполняется одно из действий в зависимости

от значения a_i^f : если a_i^f ∈ A ∪ {D}, в обозреваемую машиной ячейку записывается символ a_i^f ; если a_i^f ∈ {L, R}, машина передвигается на одну

ячейку влево, при a_i^f = L, или на одну ячейку вправо, при a_i^f = R.

В каждый следующий момент времени, если машина Тьюринга находится в состоянии q_i и обозревает некоторую ячейку, в которой

записан символ a ∈ {D}∪A, в программе ищется команда q_ia → q_j b. Если

такая команда не будет найдена, машина останавливается. Если команда

найдется, выполняются соответствующие действия, как для первого шага работы.

Если машина Тьюринга останавливается, то говорят, что эта машина принимает слово α, а оставшееся на ленте слово β (или несколько слов, разделенных пустым символом) считается результатом ее работы.

Замечание 3.1.1 . Можно заметить, что машина Тьюринга удовлетворяет всем пунктам интуитивного определения алгоритма:

1. Входные данные. Входными данными машины Тьюринга является информация на ленте перед началом работы.

2. Выходные данные. Результатом работы машины Тьюринга является содержание ленты после ее остановки.

3. Определенность. Условие на программу, не допускающее двух команд с одинаковой левой частью, гарантирует, что в любой момент времени у нас будет не более одной подходящей команды для следующего шага.

4. Элементарность. Все возможные действия машины Тьюринга сводятся к сдвигам головки на одну позицию, а также чтению/записи символа из/в текущую ячейку.

5. Конечность. По своему определению машина Тьюринга может не остановиться. Отвественность за конечность ее работы лежит на программе.

Пример 3.1.1 . Машина M₃. A = {1}, Q = {q₁, q₂, q₃}.

I : q₁D → q₁1

q₁1 → q₂L

q₂D → q₂1

q₂1 → q₃L

q₃D → q₃1

Пусть, в начале работы на ленте записано слово Λ - пустое слово (все ячейки на ленте содержат пустой символ). Тогда в по окончании работы на ленте будет слово 111.

Выпишем конфигурации, в которых будет находится машина M₃ в процессе своей работы (рис. 17).

			q1
D	D	D		D	D - начальная конфигурация
				q1
D	D	D		1	D
		q2
D	D	D		1	D
		q2
D	D	1		1	D
	q3
D	D	1		1	D
	q3
D	1	1		1	D - конечная конфигурация

Рисунок 17: Конфигурации в процессе рабоы машины M₃

Очевидно, что аналогично можно построить машину M_n с n состояниями, которая будет строить на пустой ленте слово из n единиц.