Алгоритм дерева
Как мы помним, для N P -полных задач не известно полиномиальных алгоритмов решения и поиск их представляется крайне сложной задачей.
Алгоритм дерева - это приближенный алгоритм решения, который применим к особому случаю симметричной задачи коммивояжера с неравенством треугольника:
Пусть G = (V, E) - полный неориентированный граф с n вершинами,
W : E → R+ - функция весов ребер:
W ((u, w)) ≤ W ((v, u)) + W ((u, w)), для всех u, v, w ∈ V . (36) При изложении алгоритма дерева нам понадобится два вспомогательных алгоритмов: построение минимального остовного
дерева (алгоритм 4.8.1) и алгоритм построения эйлерова цикла.
Алгоритм построения эйлерова цикла напоминает структуру доказательства теоремы 4.7.2 (рис. 47).
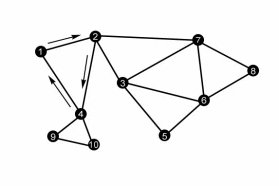
Рисунок 47: Поиск эйлерова цикла
Пусть дан эйлеров граф G = (V, E) - связный и все вершины имеют четные степени.
Алгоритм 4.9.1 (Эйлеров цикл).
function ЭЙЛЕР (H, v1) { if (degH (v1) = 0) { ЭЙЛЕР=(v1)
} else {
1. Построить любой цикл (v1, v2, ..., vk, v1), который ни по одному ребру не проходит дважды: (vi, vi+1) /= (vj , vj+1), 1 ≤ i, j ≤ k
2. H = H − (v1, v2) − (v2, v3) − · · · − (vk, v1)
3. ЭЙЛЕР = (ЭЙЛЕР(H, v1), ЭЙЛЕР(H, v2), ..., ЭЙЛЕР(H, vk), v1)
}
}
main() {
v = любая вершина из V ω = ЭЙЛЕР(G, v)
}
Замечание 4.9.1 . Заметим, что параметр H в функции ЭЙЛЕР передается по ссылке. То есть все преобразования, которые производятся с графом в функции, (удаление ребер) оказывают воздействие на исходный объект G. Таким образом, если мы удалили некоторые ребра в одной из ветвей рекурсивных вызовов функции, то ребра будут отсутствовать для всех последующих вызовов, в том числе в других ветвях рекурсии.
На вход алгоритма дерева подается граф G = (V, E) и функция весов
W : E → R+, удовлетворяющая неравенству треугольника.
Алгоритм 4.9.2 (Алгоритм дерева).
T = (V, E1) = Минимальное Остовное Дерево (G)
H = мультиграф, полученный удвоением ребер из дерева T
ω = ЭЙЛЕР(H, v), где v - любая из вершин V
τ = (Удалить повторение вершин (ω), v)
Пример 4.9.1 . Предположим, что мы уже нашли минимальное остовное дерево и удвоили его ребра. Результат изображен на рисунке
48. В ходе выполнения алгоритма поиска эйлерова цикла мы могли
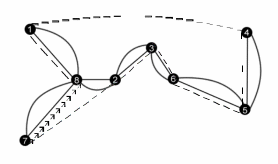Рисунок
48:
Построение
гамильтонова
цикла
с
помощью
алгоритма
дерева
обойти сначала, скажем, цикл (1,8,1). Тогда искомый цикл должен получиться в результате вызова функций в выражении
ω = (ЭЙЛЕР(H,1), ЭЙЛЕР(H,8), 1).
Вершина 1 к этому моменту уже имеет степень 0, так что ЭЙЛЕР(H,1) = (1).
ЭЙЛЕР(H,8) может найти, например, цикл (8, 2, 3, 2, 8). В этом случае мы выполним вызов (ЭЙЛЕР(H,8),ЭЙЛЕР(H,2),ЭЙЛЕР(H,3),ЭЙЛЕР(H,2),8). Здесь
ЭЙЛЕР(H,2) = (2) в обоих случаях. ЭЙЛЕР(H,8) мог бы оказаться (8,7,8), а ЭЙЛЕР(H,3) - (3,6,5,4,5,6,3).
Подставим эти циклы в (ЭЙЛЕР(H,8),ЭЙЛЕР(H,2),ЭЙЛЕР(H,3),ЭЙЛЕР(H,2),8)
и получим (8,7,8,2,3,6,5,4,5,6,3,2,8). Теперь подставим это вместо ЭЙЛЕР(H,8) в выражение для ω и получим эйлеров цикл
ω = (1, 8, 7, 8, 2, 3, 6, 5, 4, 5, 6, 3, 2, 8, 1).
После удаления повторений в этой последовательности получим цикл τ = (1, 8, 7, 2, 3, 6, 5, 4, 1) (на рисунке 48 изображен пунктирной линией). Это и есть результат работы алгоритма - гамильтонов
цикл.
Степень близости веса полученного в алгоритме дерева гамильтонова цикла к оптимальному описывает следующая теорема.
Определение 4.9.2 . Пусть τopt(G, W ) - оптимальный цикл в задаче коммивояжера для графа G и функции весов W , а τA(G, W ) - маршрут полученный с помощью некоторого алгоритма A.
Тогда алгоритм A называют ε-приближенным, если
W (τA(G, W )) − W (τopt(G, W )) ε.
W (τopt(G, W )) ≤
Утверждение 4.9.11 . Алгоритм дерева - 1-приближенный алгоритм.
Доказательство. Пусть τopt(G, W ) - оптимальный цикл в задаче коммивояжера для графа G и функции весов W , а τT (G, W ) - маршрут полученный с помощью алгоритма дерева. Так же предполагаем, что функция W удовлетворяет неравенству треугльника (36), поскольку в прочих случаях алгоритм дерева мы не рассматриваем.
При удалении любого ребра e из τopt(G, W ) мы получим некоторое остовное дерево графа G. Вес этого дерева не может быть меньше веса минимального остовного дерева T графа G. Следовательно,
W (τopt(G, W )) > W (τopt(G, W ) − e) ≥ W (T ).
С другой стороны τT (G, W ) построен из T с удвоенными ребрами (и весом 2W (T )) заменой последовательностей ребер
(vi1 , vi2 ), (vi2 , vi3 ), ..., (vij
1 , vi ) на одиночные ребра (vi , vi ). Из
− j 1 j
неравенства треугольника следует, что
W ((vi1 , vi2 )) + W ((vi2 , vi3 )) + · · · + W ((vij−1 , vij )) ≥ W ((vi1 , vij )).
Таким образом, W (τT (G, W )) ≤ 2 · W (T ) и следовательно
W (τT (G, W )) ≤ 2 · W (τopt(G, W )).
Осталось записать формулу для E-приближенности.
W (τT (G, W )) − W (τopt(G, W ))
W (τopt(G, W )) ≤
2W (τopt(G, W )) − W (τopt(G, W ))
W (τopt(G, W ))
= 1.
D
Хотя мы и не можем пока ответить на вопрос о существовании
полиномиального алгоритма для N P -трудной задачи коммивояжера, в некоторых случаях (при выполнении дополнительных условий) мы можем находить приближенное решение этой задачи.