Санкт-Петербургский государственный университет

Факультет Прикладной Математики – Процессов Управления

Задача о клике

Курсовая работа

Студента 1 курса

Очного отделения

Попова Алексея Павловича

Проверил:

к.ф.-м.н. старший преподаватель

Зараник Ульяна Петровна

Санкт – Петербург

2013

Оглавление

1. Определение клики и графа………………………………3

2. Теория NP-полных задач………………………………….4

   1. Алгоритмы и машина Тьюринга…………………….4

   2. Машина Тьюринга……………………………………..4

   3. Процесс функционирования машины Тьюринга….4

   4. Сложность алгоритма………………………………….6

   5. Полиноминальная сводимость……………………….8

   6. Классы задач в форме распознавания свойств…….9

   7. NP – полные задачи…………………………………….11

3. Задача о клике………………………………………………11

4. Алгоритмы поиска клики…………………………………12

Список использованной литературы. …………………..14

Задача о клике.

1. Определения клики и графа.

Задача о клике – это NP полная задача по поиску клики в неориентированном графе. Сама задача разбивается на две подзадачи:

1. Поиск клики в неориентированном графе размера k.

2. Поиск клики максимальной длинны

Клика – это подмножество вершин, каждые две из которых соединены ребром графа. Или, что то же самое, полный подграф исходного графа. Перейдем к более строгим, математическим определениям.

Конечным графом G=(X, α) называется пара, где X конечное множество вершин, а α – бинарное отношение на X. Если α – симметричное отношение, то граф называют неориентированным.

Если вершины x и y находятся в отношении α, то пишут xαy и говорят, что они смежные, а связь между ними осуществляется с помощью ребра, ориентированного от x к y. В неориентированном графе для любого x,y из X одновременно x α y и y α x.

Каждому бинарному отношению α на X можно сопоставить функцию F:X → X следующим образом: y ∈ F(x) ⇔ x α y. Тогда граф можно определить как пару G=(X,F), где F:X → X есть отображение, которое каждому x ∈ X ставит в соответствие подмножество Fx ⊆ X.

Граф G’=(V’,E’) называется подграфом графа G=(V,E), если V’ ⊆ V и E’ ⊆ {e | e=(u,v) ∈ E, u,v ∈ V’}. Такой граф иногда называют подграфом порожденным множеством вершин V’, поскольку он включает все ребра графа G, которые соединяют вершины из V’.

Кликой графа называется максимальный по включению вершин полный подграф графа. Таким образом, поиск наибольшей клики графа то же, что и поиск наибольшего полного подграфа графа.

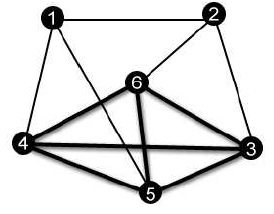Рисунок 1: Наибольшая клика графа

Неизвестно эффективного алгоритма, решающего эту задачу. Переформулируем эту задачу в форме распознавания: Дан граф G и b ∈ R+. Ответить на вопрос существует ли в этом графе полный подграф размера b? Эта задача является NP-полной задачей.

2. Теория np-полных задач.

1. Алгоритмы и машина Тьюринга

Интуитивно алгоритм можно рассматривать как последовательность действий, которая обладает рядом свойств.

1) Входные данные. Поскольку алгоритм решает некоторую общую задачу, он обычно получает некоторые инициирующие данные, в зависимости от которых выполняется.

2) Выходные данные. Любой алгоритм должен давать какой-то результат от своего выполнения.

3) Определенность. В каждый момент времени мы должны точно знать, какое действие выполнить следующим.

4)Элементарность. Это свойство значит, что каждый шаг алгоритма должен быть достаточно прост, чтобы его выполнение не требовало разбиения на меньшие шаги.

5) Конечность. Чтобы выдать результат алгоритм обычно должен завершить свою работу.

Для того чтобы дать строго формальное определение алгоритма, введем понятие машины Тьюринга.

2.2 Машина Тьюринга

Машиной Тьюринга называется совокупность пяти объектов (A, D, Q, q1, I):

1. Алфавит A = {a1, ..., an} - множество символов данной машины Тьюринга; |A| ≥ 1. Иногда алфавит называют множеством внешних состояний машины Тьюринга.

2. Пустой символ D ∈/ A.

3. Множество состояний Q = {q1, ..., qk}, |Q| ≥ 1. В некоторых случаях это множество также называют множеством внутренних состояний машины Тьюринга.

4. Начальное состояние q1 ∈ Q.

5. Программа I - множество команд вида qia → qjb, где qi, qj ∈ Q, a ∈ {D} ∪ A, b ∈ {D, L, R} ∪ A. Здесь L и R выделенные символы, такие что L, R ∈/{D} ∪ A. Кроме того, для любых qi ∈ Q и a ∈ {D} ∪ A в программе I может быть не больше одной команды qia → qjb (иными словами, в I нет двух команд с одинаковой левой частью).

2.3 Процесс функционирования машины Тьюринга.

Машина Тьюринга (рисунок 2) состоит из бесконечной в обе стороны ленты, разбитой на одинаковые ячейки, а также читающе-пишущей головки. В ячейках ленты могут быть записаны символы алфавита или пустой символ.

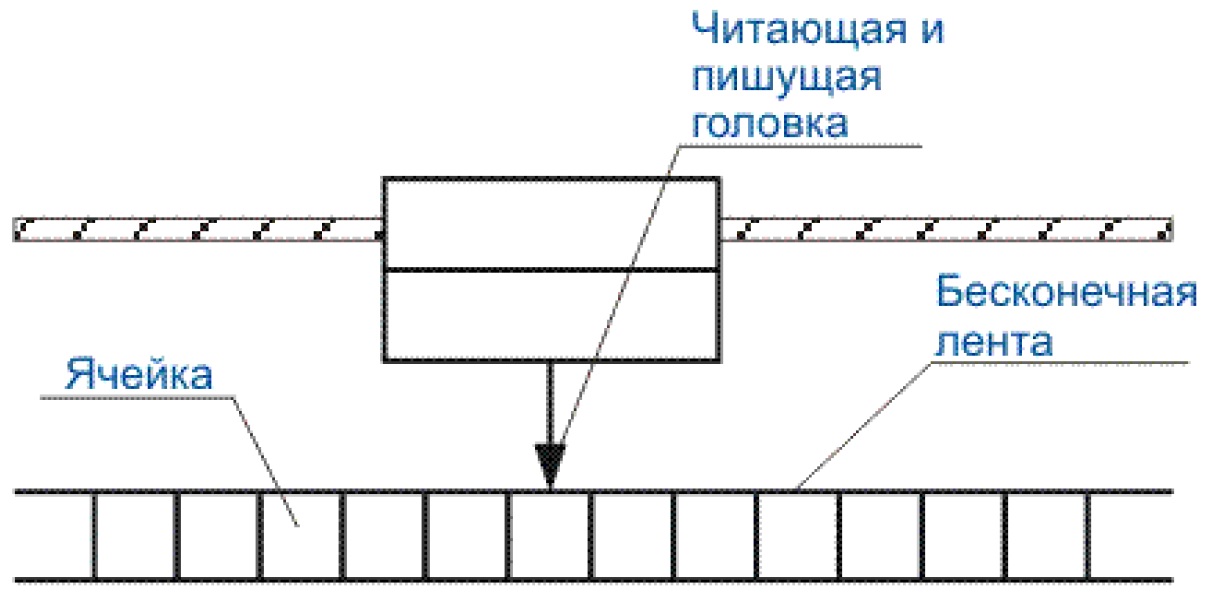Рисунок 2: Машина Тьюринга.

Работа машины Тьюринга понимается следующим образом (рисунок 3). В начальный момент времени на ленте записано конечное слово α в алфавите A (или несколько слов разделенных пустым символом D) окруженное слева и справа бесконечным количеством пустых символов D; машина Тьюринга находится в состоянии q1 и ее головка обозревает самую левую ячейку слова α. Пусть там записан символ ai1 . В I ищется команда с q1ai1 в левой части. Если такая команда не найдется, машина останавливается. Если команда найдется и это q1ai1 → qtaif, машина переходит в состояние qt и выполняется одно из действий в зависимости от значения aif: если aif ∈ A ∪ {D}, в обозреваемую машиной ячейку записывается символ aif ; если aif ∈ {L, R}, машина передвигается на одну ячейку влево, при aif = L, или на одну ячейку вправо, при aif = R.

В каждый следующий момент времени, если машина Тьюринга находится в состоянии qi и обозревает некоторую ячейку, в которой записан символ a ∈ {D}∪A, в программе ищется команда qia → qj b. Если такая команда не будет найдена, машина останавливается. Если команда найдется, выполняются соответствующие действия, как для первого шага работы.

Если машина Тьюринга останавливается, то говорят, что эта машина принимает слово α, а оставшееся на ленте слово β (или несколько слов, разделенных пустым символом) считается результатом ее работы.

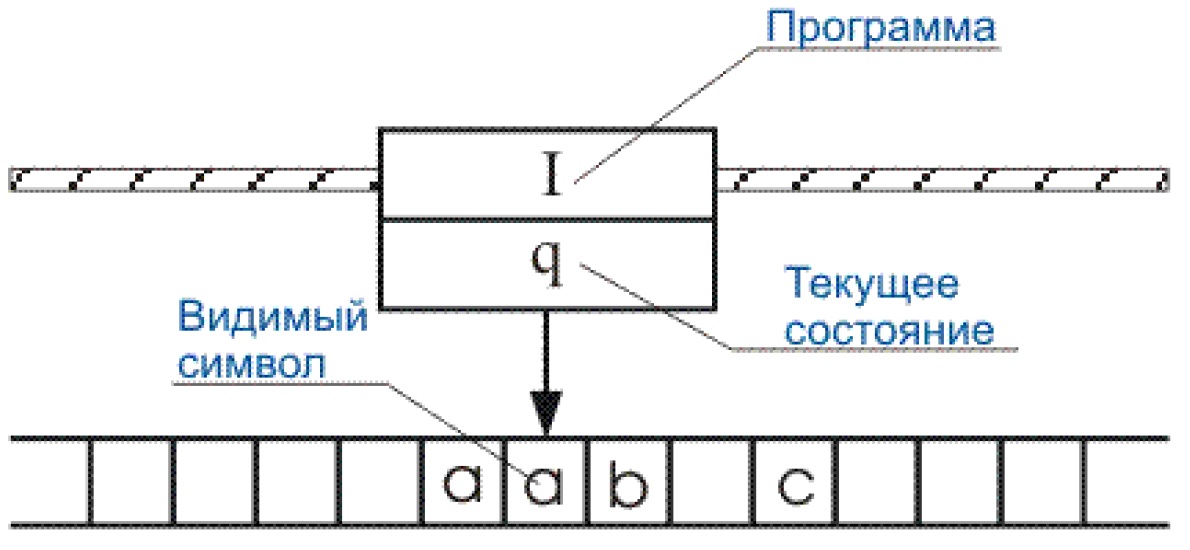
Можно заметить, что машина Тьюринга удовлетворяет всем пунктам интуитивного определения алгоритма:

1) Входные данные. Входными данными машины Тьюринга является информация на ленте перед началом работы.

2) Выходные данные. Результатом работы машины Тьюринга является содержание ленты после ее остановки.

3) Определенность. Условие на программу, не допускающее двух команд с одинаковой левой частью, гарантирует, что в любой момент времени у нас будет не более одной подходящей команды для следующего шага.

4) Элементарность. Все возможные действия машины Тьюринга сводятся к сдвигам головки на одну позицию, а также чтению/записи символа из/в текущую ячейку.

5) Конечность. По своему определению машина Тьюринга может не остановиться. Ответственность за конечность ее работы лежит на программе.