2.5 Полиноминальная сводимость.

Если один из алгоритмов имеет полиномиальную сложность, а другой требует, например, экспоненциального количества шагов (памяти), как показано выше, использование экспоненциальных алгоритмов может иметь смысл только для небольших входных параметров задачи. На больших данных любой полиномиальный алгоритм будет лучше любого экспоненциального.

В случаях, когда для двух алгоритмов, решающих одну задачу, известна полиномиальная оценка сложности, имеет смысл находить наиболее точно приближенное к величине сложности значение полиномов и сравнивать их сначала по максимальной степени, а если она окажется одинаковой, по коэффициенту перед максимальной степенью.

Принципиально иная ситуация имеет место в том случае, если вопрос о существовании полиномиального алгоритма решения некоторой задачи остается открытым. Тогда в первую очередь нужно выяснить ответ на этот вопрос и потом предпринимать действия по дальнейшей оптимизации. Если ответ положительный, можно пытаться искать наилучший из полиномиальных алгоритмов решения. Если полиномиального алгоритма решения задачи не существует, имеет смысл рассмотреть возможность нахождения "быстрого" алгоритма приближенного решения задачи.

При выяснении существования для задачи полиномиального алгоритма, все оценки можно делать с точностью до полиномиальных преобразований. Например, перед решением задачу можно преобразовать в другую форму, если затраты на этот процесс не превысят полиномиальное время, поскольку это не скажется на выводе о существовании полиномиального алгоритма для исходной задачи.

Помочь доказать существование или отсутствие полиномиального алгоритма решения некоторой задачи может понятие полиномиальной сводимости.

Пусть имеются две массовые задачи S1 и S2. Пусть A1 - произвольный алгоритм решения задачи S1. Пусть существуют два алгоритма полиномиальной сложности P21 и P12: P21 получает на входе описание индивидуальной задачи типа S2 и преобразует его в описание некоторой индивидуальной задачи типа S1; P12 получает на вход решение задачи типа S1 и преобразует его в решение задачи типа S2.

Если алгоритмы P21 и P12 таковы, что после преобразования описания индивидуальной задачи S2 алгоритмом P21 в описания индивидуальной задачи S1, решения полученной задачи S1 и преобразования полученного решения с помощью P12, мы получим решение исходной индивидуальной задачи S2, говорят, что задача S2 полиноминально сводится к задаче S1, и пишут S2 ∝ S1 (рисунок 4).

Рисунок 4. Полиноминальная сводимость.

Иными словами, S2 ∝ S1, если связка алгоритмов A2 = P12A1P21 решает индивидуальную задачу s типа S2:

P12(A1(P21(условия s))) = ответ на s.

2.6 Классы задач в форме распознавания свойств.

Будем говорить, что задача сформулирована в форме распознавания свойств, если ответ на задачу "Да" или "Нет". Если нам встретилась задача не в форме распознавания, ее можно переформулировать таким образом, чтобы она попала в наш класс задач. Например, рассмотрим следующую задачу:

Дана контурная карта с обозначенными на ней n странами и требуется раскрасить ее в разные цвета таким образом, чтобы любые два государства, соприкасающиеся участком границы, имели различный цвет.

Задача в оптимизационной форме: Дана контурная карта. Требуется раскрасить ее в минимально возможное число цветов.

Задача, переформулированная в форме распознавания свойств: Дана контурная карта и число k. Существует ли допустимая раскраска этой карты в k цветов.

Очевидно, если решена задача в оптимизационной форме, то ответ на переформулированную задачу в форме распознавания будет получен простым сравнением полученного минимального числа цветов со значением k. Следовательно, в форме распознавания задача не становится сложнее исходной задачи.

С другой стороны, если решена задача в форме распознавания, может быть решена задача о нахождении числа цветов в минимальной раскраске. Для ее решения достаточно перебрать все k от 1 до n. То есть, сложность задачи нахождения минимального числа цветов в допустимой раскраске не выше n * T (n), где T (n) – оценка сложности алгоритма решения задачи в форме распознавания. Эта задача полиноминально эквивалентна задаче в форме распознавания.

Рассмотрим два класса задач в форме распознавания свойств, - P и NP.

Класс P определяется, как класс всех задач в форме распознавания, для которых существует полиномиальный алгоритм решения. К классу P, например, относятся переформулированная в форме распознавания свойств задача нахождения минимального элемента массива:

Дан массив чисел длины n и номер ячейки k. Правда ли, что в k-той ячейке находится минимальный элемент массива. Сложность решения этой задачи O(n)

Класс NP (от Non-deterministic Polynomial) определяется, как класс всех задач в форме распознавания, для которых существует недетерминированная машина Тьюринга, вычисляющая ответ на эту задачу за полиномиальное время.

Недетерминированная машина Тьюринга отличается от машин детерминированных тем, что в ее программе допускается наличие нескольких команд с одинаковой левой частью. Другими словами, в некоторый момент времени недетерминированная машина Тьюринга может оказаться в конфигурации, из которой у нее определено более чем один вариант дальнейших действий. Таким образом, условие определенности алгоритма здесь не выполняется. В общем случае у недетерминированного алгоритма есть целое дерево различных вариантов хода выполнения.

Что делать, если мы столкнулись с такой развилкой? В таком случае недетерминированная машина может копировать себя необходимое число раз и все копии начинают выполнять каждая свою возможную последовательность действий. Копии машины работают независимо и одновременно (рисунок 5). Как только хотя бы одна копия машины заканчивает вычисления с ответом "Да", все копии завершают свою работу. В случае отрицательного ответа, машина может не остановиться.

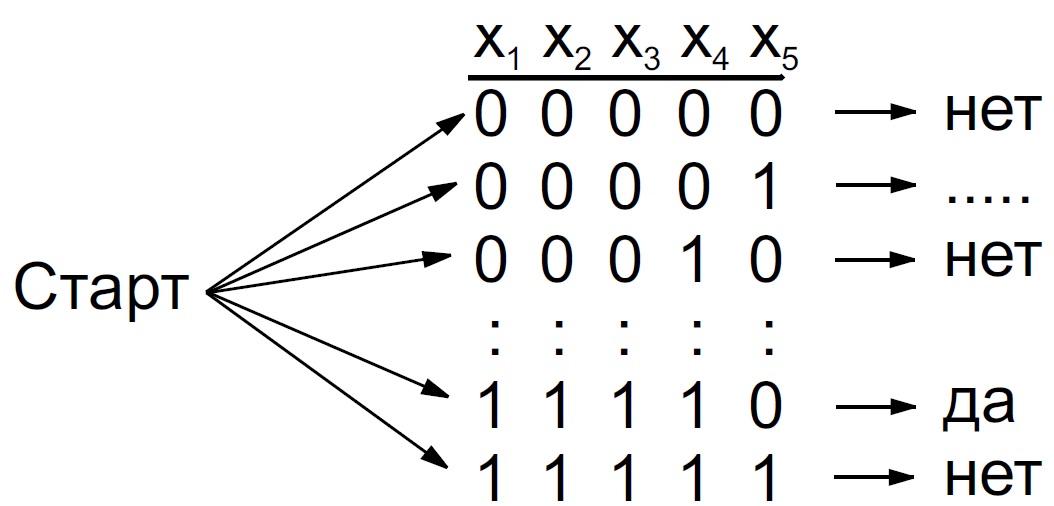
Рисунок 5: Схема работы недетерминированного алгоритма.

Можно также говорить об угадывающем устройстве. Тогда считаем, что подойдя к развилке, машина безошибочно угадывает, какой именно переход нужно выбрать, чтобы получить ответ "Да", если это возможно.

Определение 3.2.9 . Говорят, что недетерминированная машина Тьюринга принимает слово α, если существует, хотя бы одна ветвь дерева вычислений, где машина останавливается и дает ответ "Да".

Можно привести альтернативное определение класса NP.

Задача в форме распознавания принадлежит классу NP, если, когда на задачу дан ответ "Да" и приведено доказательство решения - некоторые дополнительные сведения, - можно за полиномиальное время проверить, что это правда.

2.7 NP -полные задачи

Следующая теорема была доказана Куком в 1971 году.

Теорема. Любая задача из класса N P полиноминально сводится к задаче о выполнимости.

Таким образом, задача о выполнимости в некотором смысле не проще всех остальных задач из класса NP. Все подобные ей задачи названы NP -полными. Или же, что то же самое, задача называется NP -полной, если она принадлежит классу NP и к ней полиноминально сводятся все задачи из класса NP.

Задача о выполнимости выглядит следующим образом: дано логическое выражение в конъюнктивной нормальной форме. Является ли функция, реализуемая этой формулой, выполнимой?

Другими словами, дана булева функция f (x1, x2, ..., xn), определенная своей КНФ: (D1) ∧ (D2) ∧…∧ (Dk). Требуется ответить на вопрос, существует ли такой набор значений логических переменных a1, a2, ..., an, что f (a1, a2, ..., an) = 1.