3. Мощность объединения множеств

Приведем еще одну задачу, которая решается с помощью принципа включения-исключения, - задачу нахождения мощности объединения пересекающихся множеств.

Задача 1.8.4 . Пусть A₁, A₂, ..., A_k - конечные множества. Пусть

A = A₁ ∪ A₂ ∪ ... ∪ A_k. Требуется найти мощность A, если известны

|A_i|, i = 1, k, и | _i∈I A_i|, I ⊆ {1, 2, ..., k}.

Пусть S = {1, 2, ..., k} и T ⊆ S. Будем говорить, что x ∈ A обладает свойством i, если x ∈ A_i. Обозначим

f₌(T ) - число элементов из A, обладающих всеми свойствами из T и не обладающих другими свойствами из S;

f_≥(T ) - число элементов из A, обладающих всеми свойствами из T . Очевидно, f_≥(T ) = | _i∈T A_i|, если T не пусто и f_≥(∅) = |A|

Тогда верна формула (19) и, следовательно, можно использовать формулу (21).

Утверждение 1.8.4 .

k

|A₁ ∪ A₂ ∪ ... ∪ A_k| = ^\ |A_i| − ^\

|A_i1

∩ A_i2 |+

+ \

1≤i₁<i₂<i₃≤k

|A_i1

i=1

∩ A_i2

1≤i₁<i₂≤k

3

∩ A_i | − · · · + (−1)^k+1|A₁ ∩ A₂ ∩ ... ∩ A_k|. (22)

Доказательство. Поскольку каждый элемент из A обладает хотя бы одним свойством из S, то f₌(∅) = 0. С другой стороны из формулы (21)

получаем

≥

0 =f₌(∅) = ^\(−1)^{|Y |}f

(Y ) = |A| + ^\ (−1)^{|Y |}| ⁿ A_i| =

Y ⊆S

k

Y ⊆S,

|Y |≥1

i∈Y

=|A| − ^\ |A_i| + ^\

|A_i1

∩ A_i2 |−

i=1

\

−

1≤i₁<i₂<i₃≤k

1≤i₁<i₂≤k

k

|A_i1 ∩ A_i2 ∩ A_i3 | + · · · + (−1)

|A₁ ∩ A₂ ∩ ... ∩ A_k|.

Перенесем все слагаемые кроме первого за знак равенства и получим искомое утверждение.

D

Часто, именно формулу (22) называют принципом включения- исключения. Тем не менее, как мы видели, с помощью принципа включения-исключения решаются и другие задачи.

4. Число целочисленных решений системы неравенств

В подразделе 1.7.1 мы показали, что число решений уравнения x₁ + x₂ +

• · · + x_k = n в неотрицательных целых числах находится по формуле (16):

n + k − 1

N₌(n, k) =

,

k − 1

а число решений неравенства x₁ + x₂ + · · · + x_k ≤ n в неотрицательных

целых числах - по формуле (17):

N_≤(n, k) =

n + k

.

k

Здесь мы расширим множество систем, для которых можно будет найти число решений.

Для начала положим, что на значения переменных наложены ограничения снизу. Пусть a_i ∈ N₀, i = 1, k, и задана система

x₁ + x₂ + · · · + x_k = n, a_i ≤ x_i, i = 1, k.

Чтобы найти число решений этой системы, достаточно сделать замену

y_i = x_i − a_i. Тогда y_i ≥ 0 и

(y₁ + a₁) + (y₂ + a₂) + · · · + (y_k + a_k) = n, y₁ + y₂ + · · · + y_k = n − a₁ − a₂ − · · · − a_k.

Согласно формуле (16) число целочисленных решений данной системы

i=1

n + k − 1 − ^):k

_ai

. (23)

k − 1

Аналогично, число решений системы

x₁ + x₂ + · · · + x_k ≤ n, a_i ≤ x_i, i = 1, k,

равно

i=1

n + k − ^):k

_ai

. (24)

k

Рассмотрим систему с ограничениями на переменные и сверху, и снизу. Пусть a_i, b_i ∈ N₀, a_i ≤ b_i, i = 1, k. Требуется найти число целочисленных

решений системы

x₁ + x₂ + · · · + x_k = n, (25)

a_i ≤ x_i ≤ b_i, i = 1, k. (26)

Пусть A - множество решений системы

x₁ + x₂ + · · · + x_k = n, (*)

a_i ≤ x_i, i = 1, k :

A = {(α₁, α₂, ..., α_k) | α₁ + α₂ + · · · α_k = n, a_i ≤ α_i, i = 1, k}.

Согласно (23)

|A| =

n + k − 1 − ^):k

i=1

k − 1

_ai

.

Обозначим A_s, s = 1, k, - множество решений системы (*), для которых не выполняется ограничение x_s ≤ b_s:

A_s = {(α₁, α₂, ..., α_k) | α₁ + α₂ + · · · α_k = n,

a_i ≤ α_i, i = 1, k, b_s + 1 ≤ x_s}.

Таким образом, все решения системы (*), которые не удовлетворяют хотябы одной верхней границе из (26), лежат в множестве A₁ ∪A₂ ∪...∪A_k.

Следовательно, число решений системы (25)-(26) равно

|A \ (A₁ ∪ A₂ ∪ ... ∪ A_k)| = |A| − |A₁ ∪ A₂ ∪ ... ∪ A_k|.

Использовав утверждение 1.8.4, получим

|A| − |A₁ ∪ A₂ ∪ ... ∪ A_k| = |A| − ^\

Y ⊆{1,...,k},

|Y |≥1

(−1)^{|Y |−1}| ⁿ A_i|. (**)

i∈Y

Теперь, чтобы найти число решений системы (25)-(26), достаточно научиться находить мощность пересечения произвольного набора множеств A_j .

Пусть Y ⊆ {1, ..., k}. Тогда

ⁿ A_j = {(α₁, α₂, ..., α_k) | α₁ + α₂ + · · · α_k = n,

j∈Y

a_i ≤ α_i, i = 1, k, b_s + 1 ≤ x_s, s ∈ Y }.

Другими словами, _j∈Y A_j есть множество решений системы

x₁ + x₂ + · · · + x_k = n,

a_i ≤ x_i, i ∈ {1, ..., k} \ Y, b_s + 1 ≤ x_s, s ∈ Y.

i=1

Тогда согласно (23)

n

|

i∈Y

A_i| =

n + k − 1 − ^):k

a_i − ^):

k − 1

j∈Y

(b_j + 1 − a_j )

.

Подставив эти значения в формулу (**), получим число решений системы (25)-(26).

Рассуждения для системы

x₁ + x₂ + · · · + x_k ≤ n, a_i ≤ x_i ≤ b_i, i = 1, k.

аналогичны рассуждениям для системы (25)-(26) с точностью до замены величины (23) на величину (24).

Пример 1.8.1 . Рассмотрим систему всего с двумя переменными:

x₁ + x₂ ≤ n, a₁ ≤ x₁ ≤ b₁, a₂ ≤ x₂ ≤ b₂, (*)

и систему без верхних ограничений на переменные:

x₁ + x₂ ≤ n, a₁ ≤ x₁, a₂ ≤ x₂. (**) Сравним графическое изображение области, в которой лежат решения системы (**) (рис. 12), и области, где находятся решения системы (*) (рис. 13). Как можно видеть, чтобы из области решений для

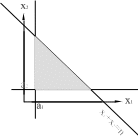Рисунок 12: Множество решений неравенства x₁ + x₂ ≤ n с нижними ограничениями

на значения переменных.

системы (**) получить область для системы (*), нужно удалить из нее объединение областей решений систем

x₁ + x₂ ≤ n, b₁ + 1 ≤ x₁, a₂ ≤ x₂,

и

x₁ + x₂ ≤ n, a₁ ≤ x₁, b₂ + 1 ≤ x₂.

Пример 1.8.2 . Пусть дана система неравенств

x₁ + x₂ + x₃ ≤ 30,

0 ≤ x₁ ≤ 10, 5 ≤ x₂ ≤ 12, 1 ≤ x₃ ≤ 8.

Обозначим за A множество целочисленных решений исходной системы без учета верхних границ на значение переменных:

x₁ + x₂ + x₃ ≤ 30,

0 ≤ x₁, 5 ≤ x₂, 1 ≤ x₃.

(∗)

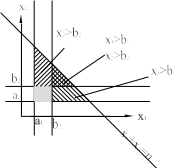Рисунок 13: Множество решений неравенства x₁ +x₂ ≤ n с ограничениями на значения

переменных сверху и снизу.

Число целочисленных решений системы (∗) вычисляем по известной формуле:

|A| =

n + k − ^): s_i

k

27 · 26 · 25

₌ 30 + 3 − 6 ₌ 3

₂₇

= 3

27!

= 3! · 24!

= = 2925.

6

Обознычим за A_i множество целочисленных решений исходной системы (∗), которые не удовлетворяют верхней границе исходной

системы на значение x_i, i = 1, 3.

_A1 _: x₁ + x₂ + x₃ ≤ 30,

11 ≤ x₁, 5 ≤ x₂, 1 ≤ x₃.

_A2 _: x₁ + x₂ + x₃ ≤ 30,

0 ≤ x₁, 13 ≤ x₂, 1 ≤ x₃.

_A3 _: x₁ + x₂ + x₃ ≤ 30,

0 ≤ x₁, 5 ≤ x₂, 9 ≤ x₃.

Посчитаем мощности этих множеств.

|A₁| =

30 + 3 − 17 ₌

3

₁₆

= 3

16!

= 3! · 13!

16 · 15 · 14 _{= 560.}

6

|A₂| =

30 + 3 − 14 ₌

3

₁₉

= 3

19!

= 3! · 16!

19 · 18 · 17 _{= 969.}

6

|A₃| =

30 + 3 − 14

3

= 969.

Также рассмотрим все возможные пересечения этих множеств и посчитаем их мощности.

A₁ ∩ A₂ :

x₁ + x₂ + x₃ ≤ 30,

11 ≤ x₁, 13 ≤ x₂, 1 ≤ x₃.

|A₁ ∩ A₂| =

30 + 3 − 25 ₌

3

₈

= 3

8!

= 3! · 5!

8 · 7 · 6 _{= 56.}

6

A₁ ∩ A₃ :

x₁ + x₂ + x₃ ≤ 30,

11 ≤ x₁, 5 ≤ x₂, 9 ≤ x₃.

30 + 3 − 25

|A₁ ∩ A₃| = ₃

= 56.

A₂ ∩ A₃ :

x₁ + x₂ + x₃ ≤ 30,

0 ≤ x₁, 13 ≤ x₂, 9 ≤ x₃.

|A₂ ∩ A₃| =

30 + 3 − 22 ₌

3

₁₁

= 3

11!

= 3! · 8!

11 · 10 · 9 _{= 165.}

6

A₁ ∩ A₂ ∩ A₃ :

x₁ + x₂ + x₃ ≤ 30,

11 ≤ x₁, 13 ≤ x₂, 9 ≤ x₃.

30 + 3 − 33

|A₁ ∩ A₂ ∩ A₃| = ₃

= 0.

Теперь количество целочисленных решений исходной системы можно получить по формуле:

|A| − |A₁ ∪ A₂ ∪ A₃| = |A| − (|A₁| + |A₂| + |A₃| − |A₁ ∩ A₂|−

− |A₁ ∩ A₃| − |A₂ ∩ A₃| + |A₁ ∩ A₂ ∩ A₃|) = 2925 − 560 − 969−

− 969 + 56 + 56 + 165 = 704.

Рассмотрим теперь систему с ограничением на сумму переменных снизу:

x₁ + x₂ + · · · + x_k ≥ n,

a_i ≤ x_i ≤ b_i, i = 1, k.

Сделаем замену переменных y_i = b_i − x_i. Тогда ограничения на значения переменных трансформируются следующим образом:

a_i ≤ b_i − y_i ≤ b_i ⇒ 0 ≤ y_i ≤ b_i − a_i.

Подставим замену в неравенство для суммы переменных:

(b₁ − y₁) + (b₂ − y₂) + · · · + (b_k − y_k) ≥ n, y₁ + y₂ + · · · + y_k ≤ b₁ + b₂ + · · · + b_k − n.

Получили систему

k

y₁ + y₂ + · · · + y_k ≤ ^\ b_i − n,

i=1

0 ≤ y_i ≤ b_i − a_i, i = 1, k,

которая может быть решена указанным выше для системы (25)-(26) способом.