4 Теория графов

Теория графов - один из основных разделов дискретной математики Основным объектом изучения является граф. Граф исходно графический объект, рисунок (рис. 32). Это способ изобразить некоторую структуру с помощью простой схемы. У графа есть некоторое количество узлов

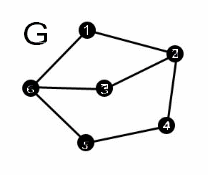
Рисунок 32: Пример графа

(точек, вершин), которые соеденины между собой линиями (ребрами).

Примером графа служит схема метрополитена. Станции - вершины графа; переезды между станциями - ребра графа.

Другим примером может служить система родственных связей в каком-нибудь городе. Вершинами такого графа служили бы все жители города. Люди, находящиеся в непосредственном родстве (братья, сестры, родитель и ребенок) были бы соеденены ребрами, а между дальними родственниками можно было бы найти цепочку из ребер близкого родства. Между людьми не находящимися в родстве в этом графе не нашлось бы никакой связи.

Теорию графов часто не интересует конкретное изображение графа и имена вершин. Основное внимание уделяется структуре: сколько вершин

имеет граф, какие из них соеденены ребрами, а для ориентированных

графов еще от к какой вершины к какой направлены ребра.

4.1 Определения графа

Существует несколько способов сказать, что такое граф, а под словом граф в разных случаях понимают структуры, отличающиеся по своим свойствам. В каждом конкретном случае, когда вы имеете дело с графами следует понимать, что имеется в виду под этим словом, и использовать те свойства, которые характерны для данного класса графов.

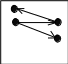
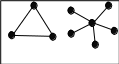
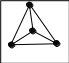_p ² ₄ 7

^{q s} 6

8

_{t 1 3} 5

9

1. ^b) c) _d)

Рисунок 33: Примеры графов

Самым наглядным способом задания графа является его графическое изображение. Само название графа появилось благодаря этому представлению. На рисунке 33 инзображены примеры графов. Графы a), b) и d) - связные; графы b) и c) - помеченные; графы a) и d) - полные, граф b) - ориентированный ¹.

Далее мы попробуем прояснить, что же такое граф и в чем особенности разных способов его определения.

1. Общее определение

Рассмотрим наиболее общее определение графа. Определения большинства понятий подразумевающихся под термином "граф" являются некоторыми сужениями этого определения.

Определение 4.1.1 . Пусть заданны конечные множества произвольной природы V и E, V /= ∅, V ∩ E = ∅, и трехместный

¹Перечисленные свойства графов будут определены в дальнейшем.

предикат P

P (x, u, y) : V × E × V 1→ {T rue, F alse}.

Будем говорить, что задан граф G = (V, E, P ) с множеством вершин

V , множеством ребер E и инцидентором P , если

1. P определен для всех упорядоченных троек (v, e, w), где v, w ∈ V и

e ∈ E;

2. (∀e ∈ E)(∃v, w ∈ V ){P (v, e, w)&(∀v^t, w^t ∈ V )[P (v^t, e, w^t) ⇒ (v =

v^t & w = w^t) ∨ (v = w^t & w = v^t)]}. То есть для любого ребра всегда

существует две вершины (не обязательно различные), которые оно

соединяет, и никакие другие две вершины не могут быть соеденины тем же ребром.

Кроме того для каждого ребра e ∈ E должно выполняться одно и только одно из соотношений:

A. (∃v, w ∈ V )[v /= w & P (v, e, w) & P (w, e, v)]

B. (∃v, w ∈ V )[v /= w & P (v, e, w) & P (w, e, v)]

C. (∃v ∈ V )P (v, e, v)

Ребро удовлетворяющее соотношению A называют неориентированным, удовлетворяющее соотношению B - ориентированным ребром или дугой;

ребра удовлетворяющие соотношению C называют петлями. Ребро e ∈ E

назовем кратным, если

(∃v, w ∈ V )(∃e₁ ∈ E)[P (v, e, w)&P (v, e₁, w)].

Определение 4.1.2 . Граф будем называть ориентированным или орграфом, если в нем отсутствуют ребра типа A (неориентированные ребра).

Граф будем называть неориентированным, если в нем отсутствуют ребра типа B (ориентированные ребра).

Если граф содержит и ориентированные и неориентированные ребра, его называют смешанным.

Неориентированные ребра рисуют линиями, соединяющими точки, соответствующие вершинам. Ориентированные ребра обозначают стрелками. При этом для ребра, для которого выполняется P (v, e, w), стрелка направлена от вершины v и к вершине w. Ориентированные ребра также называют дугами. Для петель ориентация не имеет смысла, так что они могут изображаться и со стрелкой и без, когда это удобно.

Определение 4.1.3 . Порядком графа G = (V, E, P ) называют число

n = |V |.

Определение 4.1.4 . Две вершины v, w ∈ V называются смежными, если (∃e ∈ E)[P (v, e, w) ∨ P (w, e, v)]

Определение 4.1.5 . Вершина v ∈ V и ребро e ∈ E инцидентны, если

(∃w ∈ V )[P (v, e, w) ∨ P (w, e, v)]

Определение 4.1.6 . Два ребра e, f ∈ E смежны, если существует вершина v ∈ V которой они оба инцидентны.

Замечание 4.1.1 . До сих пор мы говорили о конечных графах. Существуте также понятие бесконечного графа, для которого множества V и E могут быть счетными. Мы такие графы рассматривать не будем.