5. Вычислимые функции

Далее в нашем курсе будем рассматривать только машины Тьюринга с алфавитом A = {1}. Каждой такой машине M соответствует частичная функция f_M : N₀ → N₀.

Определение 3.1.10 . Пусть, M - машина Тьюринга. Тогда, для любого i ∈ N₀,



^ L(β), f_M (i) =



если M (11...1) = DqβD - стандартная

i

конечная конфигурация;

^ неопред., иначе.

Пример 3.1.2 . Машина M_×2. A = {1}, Q = {q₁, q₂, ..., q₉}.

α = 111...1 - слово из n единиц. β = 111...1 - слово из 2n единиц.

Программа машины M_×2 представлена графом переходов на рисунке 19.

Выпишем конфигурации, в которых будет находиться машина M_×2 в процессе своей работы, если α = 1 (рисунок 20). Результатом работы оказывается слово 11, что соответствует удвоенному входному слову.

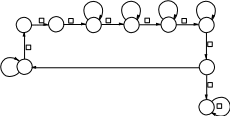1:R

1:R

^1:R 1:L

q

q

q

q

1: :R ^:R

₁ 2 3 ₄

:R

^:1 :1

q

q

⁵ 6

:L

1:L ^q₈

1:L _q7

:R

_q9 :R

Рисунок 19: Граф переходов машины удвоения

D	q11	D	D	D	D
D	q2D	D	D	D	D
D	D	q3D	D	D	D
D	D	D	q4D	D	D
D	D	D	q51	D	D
D	D	D	1	q5D	D
D	D	D	1	q61	D
D	D	D	q61	1	D
D	D	q6D	1	1	D
D	q7D	D	1	1	D
D	D	q9D	1	1	D
D	D	D	q91	1	D

Рисунок 20: Конфигурации в процессе работы машины M_×2

Работа машины M_×2 на входном слове из двух и более единиц рассматривается аналогично.

×2

Очевидно, f_M

(i) = 2i для любых i ∈ N₀.

Определение 3.1.11 . Функция f : N₀ → N₀ называется вычислимой,

если существует такая машина Тьюринга M , что f = f_M . В

противномслучае,f-невычислимаяфункция.

Утверждение 3.1.1 (О существовании невычислимых функций).

Существует невычислимая функция f : N₀ → N₀.

Доказательство. 1) Для начала покажем, что множество машин Тьюринга счетно.

Во-первых, множество машин Тьюринга не может быть конечным. Мы ранее упомянали, что для любого n ∈ N можно построить машину

M_n, с n состояниями, которая рисует n единиц, начиная работу с пустой ленты. Если мы построим последовательность машин Тьюринга M₁, M₂,

..., M_n, ..., которая будет иметь счетную длину. Значит, множество машин Тьюринга не менее, чем счетно.

Как было замечено ранее в параграфе 3.1.3, машина Тьюринга практически полностью определяется своей программой. Значит, чтобы пересчитать различные машины Тьюринга, достаточно пересчитать различные программы.

Сопоставим любому множеству команд I, отвечающих определению программы машины Тьюринга число как описано ниже.

Рассмотрим алфавит X = {D, 1, ∗, L, R}. Пусть D < 1 < ∗ < L < R.

Тогда на множестве слов алфавита X можно определить строгий

линейный (например, лексикографический) порядок. Пронумеруем все слова алфавита X следующим образом: сначала по порядку идут все слова алфавита X длины 1, следующие номера получают в том же порядке слова длины 2, затем - длины 3 и так далее. Так мы пронумеруем натуральными числами все слова алфавита X. Каждой

команде программы q_ia → q_j b сопоставим слово

∗...∗ a ∗...∗ b

i

j

в алфавите X. Такое слово однозначно описывает команду. Действительно, для определения состояний нам достаточно знать их номера (никакая другая информация об элементах множества Q машиной

Тьюринга не используется), а для любых a ∈ {D} ∪ A = {D, 1},

b ∈ {D, L, R} ∪ A = {D, L, R, 1} у нас имеются подходящие символы в

алфавите X.

Программе I можно сопоставить конкатенацию таких слов; очевидно, что разным программам не могут соответствовать совпадающие конкатенации и по такой конкатенации можно однозначно восстановить исходную программу. Но, поскольку команды в программе не упорядочены, одной программе могут соответствовать записи, полученные одна из другой изменением порядка команд. Из всех записей, сопоставленных одной и той же программе будем выбирать ту, номер которой, в выбранной ранее нумерации всех слов алфавита X, будет наименьшим; этот номер сопоставим программе I.

Таким образом, все различные программы машин Тьюринга пронумерованы числами из некоторого подмножества множества натуральных чисел и, следовательно, число машин Тьюринга не более чем счетно.

С другой стороны, множество машин Тьюринга не может быть конечным. Чтобы показать это, достаточно вспомнить про множество

машин Тьюринга M_n, i = 1, ∞, из примера 3.1.1, которые рисуют n

единичек, начиная работу с пустой ленты. Все эти машины различны

и их счетное число. Следовательно число машин Тьюринга счетно.

2. Теперь покажем, что число частичных функций f : N₀ → N₀ более

чем счетно.

Рассмотрим множество всех частичных функций N₀ → N₀:

A = {f | f : N₀ → N₀}

и рассмотрим подмножество этого множества

B = {f | f : N₀ → {0, 1}, f - всюду определена на N₀}.

Если мы докажем, что множество B более чем счетно, то, очевидно, это будет верно и для множества A.

Предположим, что множество B счетно. Тогда все функции из B можно пронумеровать натуральными числами. Пусть тогда,

B = {f₁, f₂, f₃, ....}.

Рассмотрим функцию f , определенную следующим выражением:

f (i) = 1 − f_i(i), i = 1, ∞. (31) По определению это функция f : N₀ → {0, 1} и всюду определена на N₀. Тогда должен существовать индекс k, которым функция f пронумерована

в множестве B, но из формулы 31 следует, что f (k) = 1 − f_k(k) /= f_k?!

Это противоречие доказывает, что как бы мы не нумеровали элементы

B, всегда найдется ненумерованная функция. Следовательно, множество B имеет несчетную мощность, а, значит, и множество A также более чем счетно.

2. Поскольку число машин Тьюринга счетно, а число частичных функций f : N₀ → N₀ более чем счетно, мы не можем сопоставить каждой

функции свою машину Тьюринга. Таким образом, должны существовать функции, которые не будут являться вычислимыми, что и требовалось доказать.

D