4.2 Изоморфизм графов

Очень важным для теории графов является понятие изоморфизма.

2

В обыкновенном графе с n вершинами может быть не более (ⁿ) ребер.

Следовательно, если рассматривать все возможные способы расстановки

₂)

ребер, оказывается, что существует всего 2⁽n

помеченных графов. При

этом, далеко не все графы различаются структурно.

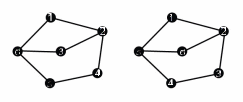На рисунке 39 изображены два графа. Очевидно, что их структура

Рисунок 39: Пример изоморфизма

ничем не различается, но строго по определению они не равны, поскольку их множества ребер не совпадают: ребро (1, 6) есть в левом гафе, но его нет в правом.

Определение 4.2.1 . Два графа G₁ = (V₁, E₁, P₁) и G₂ = (V₂, E₂, P₂)

изоморфны, если существуют биекции ϕ : V₁ 1→ V₂ и ψ : E₁ 1→ E₂,

такие что

(∀v, w ∈ V₁)(∀e ∈ E₁)[P₁(v, e, w) ⇔ P₂(ϕ(v), ψ, (e), ϕ(w))].

Несложно показать, что изоморфизм на множестве графов является отношением эквивалентности. Действительно, чтобы доказать рефлексивность, достаточно взять в качестве ϕ и ψ

тождественные отображения V₁ 1→ V₁ и E₁ 1→ E₁. Симметричность

доказывается, использованием в качестве искомых отображений ϕ⁻¹

и ψ⁻¹. Транзитивность будет следовать из биективности композиции

биективных отображений.

Таким образом по свойству отношений эквивалентности все множество графов делится на классы, любые два графа в которых - изоморфны. В дальнейшем, когда нам не будут принципиальны особенности конкретных графов, мы будем обращаться со всем классом изоморфных графов, как с одним и тем же графом.

^{Запись G}₁ ^∼= ^G₂ ^{в дальнейшем будет значить, что графы G}₁ ^{и G}₂

изоморфны.

Для обыкновенных графов и графов Бержа определение изоморфизма можно можно переформулировать проще.

Определение 4.2.2 . Графы G₁ = (V₁, E₁) и G₂ = (V₂, E₂) называют изоморфными, если существует такая биекция ϕ : V₁ → V₂, что

∀u, v ∈ V₁, (u, v) ∈ E₁ ⇔ (ϕ(u), ϕ(v)) ∈ E₂. (32) Пример 4.2.1 . Рассмотрим графы на рисунке 40. Выберем отображение ϕ следующим образом

v ϕ(v) 1 1

2 2

3 4 .

4. 3

5. 6

6. 5

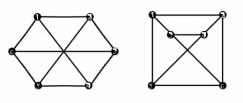
Рисунок 40: Изоморфные графы

Несложно убедиться, что условие (32) для графов на рисунке 40 выполняется.

Далее, можем говорить о помеченных и непомеченных графах. Будем говорить, что граф помеченный, если каждая вершина графа имеет индивидуальное имя. С помеченными графами имеют дело, когда необходимо хранить какую-то индивидуальную информацию о каждой вершине. Если же нам интересна только структура графа, а конкретные названия вершин не имеют значения, можно говорить, что граф непомеченный и рассматривать его с точностью до изоморфизма.

4.2.1 Инварианты графа

Определение 4.2.3 . Функции, принимающие одинаковые значения для изоморфных графов называются инвариантами.

Определение 4.2.4 . Систему инвариантов назовем полной системой инвариантов, если, из того что для некоторых двух графов все эти инварианты принимают одинаковые значения, следует, что данные графы изоморфны.

Приведем примеры инвариантов графа.

Пример 4.2.2 . 1) Простейшими примерами инвариантов графа G

являются n = |V (G)| и m = |E(G)| - количества вершин и ребер графа.

Очевидно, что у всех изоморфных графов эти значения совпадают.

2. Другим инвариантом ялвяется вектор степеней вершин, упорядоченных по возрастанию: (d₁, d₂, . . . , d_n).

3. Хроматическое число.

Определение 4.2.5 . Хроматическим числом графа G назовем наименьшее целое число χ(G), такое что существует разбиение

множества вершин графа V (G) = V₁ ∪ V₂ ∪ · · · ∪ V_χ(G), удовлетворяющее

следующему условию

(∀x, y ∈ V_i)(∀e ∈ E(G))P (x, u, y), i = 1, χ(G).

Другими словами ни в одном подмножестве V_i нет смежных вершин.

Заметим, что графы с χ(G) = 2 и χ(G) = 1 будут двудольными.

2. Размер максимальной клики в графе (плотность). Кликой будем называть полный подграф графа G. Количество вершин максимальной клики в графе G обозначается ω(G); иногда это значение называют плотностью графа и обозначают ϕ(G).

Очевидно, что ω(G) ≤ χ(G), поскольку в каждое множество

V_i из определения хроматического числа может не может входить

болше одной вершины из максиальной клики. Графы, для всех подграфов которых выполняется равенство ω(G) = χ(G), называются совершенными.

2. Число вершинной независимости (неплотность). Независимым множеством вершин графа G назовем множество вершин какого- нибудь пустого подграфа G, то есть множество попарно несмежных вершин. Числом вершинной независимости α(G) (неплотностью) называется число вершин в максимальном независимом множестве графа G. Очевидно α(G) = ω(G).

3. Размер минимального кликового покрытия. Размером минимального кликового покрытия графа G назовем наименьшее число χ(G) клик G₁, G₂, . . . , G_χ(G) графа G, удовлетворяющих условию

(∀v ∈ V (G))(∃G^t ∈ {G₁, G₂, . . . , G_χ(G)})[v ∈ V (G^t)]

Нетрудно видеть, что χ(G) = χ(G). Также легко доказывается неравенство α(G) ≤ χ(G).