3. Матрицы, связанные с графом

Одним из удобных математических представлений графа является задание связанных с ним матриц. Две самых распространенных из них

- это матрица смежности и матрица инцидентности, которые хранят информацию соответственно об отношении смежности между вершинами и отношении инцидентности между вершинами и ребрами.

1. Матрица смежности

Пусть G = (V, E) - неориентированный граф, V = {1, 2, ..., n}. Матрица смежности A(G) для графа G представляет собой квадратную (0,1)-

матрицу n × n. Элементы a_i,j (G) матрицы A(G) заданы следующим

соотношением:

a_i,j (G) =

⁽ 1, (i, j) ∈ E(G) _{. (33)}

0, (i, j) ∈/ E(G)

Матрица смежности обыкновенного графа симметрична, поскольку

(i, j) ∈ V (G) ⇔ (j, i) ∈ V (G).

На диагонали стоят нулевые элементы, поскольку не допускаются

петли.

Сумма элементов по i-той строке или по i-тому столбцу равна степени вершины i.

Сумма всех элементов матрицы смежности равна удвоенному числу

ребер графа:

n n

^{\ \} a_i,j (G) = 2|E(G)|.

i=1

j=1

Пример 4.6.1 . Рассмотрим граф на рисунке 43. Матрица смежности этого графа имеет следующий вид.

^0 1 0 0 1^

^1 0 1 0 1^

A(G) = 0 1 0 1 0 .

 

 

^0 0 1 0 0^

1 1 0 0 0

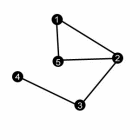
Рисунок 43: Неориентированный граф

Для графа Бержа определение матрицы смежности выглядит так же, как описано в (33), но ребра уже будут считаться ориентированными, так что и симметричности матрицы может не быть. Так же диагональ матрицы смежности для графа Бержа может быть не нулевой, так как он допускает петли.

Сумма элементов по i-той строке равна полустепени исхода вершины i. Сумма элементов по j-тому столбцу равна полустепени захода вершины j.

Сумма всех элементов матрицы смежности ориентированного графа равна числу дуг графа:

n n

^{\ \} a_i,j (G) = |E(G)|.

i=1

j=1

Пример 4.6.2 . Рассмотрим граф на рисунке 44. Матрица смежности этого графа имеет следующий вид.

^0 0 0 0 1^

^1 0 1 0 0^

A(G) = 0 0 0 1 0 .

 

 

^0 0 0 0 0^

0 1 0 0 0

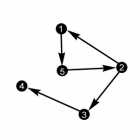
Рисунок 44: Ориентированный граф

Замечание 4.6.1 . Если мы захотим определить матрицу смежности для мультиграфа или псевдографа, придется выйти за рамки значений 0 и 1. Например, можно сказать, что элемент a_i,j (G) равен числу ребер (дуг) соединяющих вершины i и j (идущих из вершины i в вершину j).

Теорема 4.6.1 . Пусть G = (V, E) - ориентированный или неориентированный граф и A(G) - его матрица смежности.

i,j

Тогда элемент a^(k), стоящий на пересечении i-той строки и j-

того столбца матрицы A^k(G) = (A(G))^k, равен числу маршрутов из вершины i в вершину j длины k, i = 1, n, j = 1, n. В случае ориентированного графа имеется в виду ориентированный маршрут.

Доказательство. Докажем по индукции. Для степени 1 утверждение верно: элемент матрицы смежности равен числу ребер из i в j.

Предположим, что формула верна для степени k − 1, где 1 < k.

Рассмотрим i, j-тый элемент A^k(G) = A^k−1(G) · A(G):

_i,t t,j

n

_a(k)

i,j ⁼

\

t=1

a^(k−1)(G) · a (G). (∗)

Здесь a^(k−1)(G) - число маршрутов из i в t длины k − 1, а a

(G)

i,t

указывает наличие или отсутствие ребра из

t,j

t в j. Таким образом

i,t

произведение a^(k−1)(G) · a

t,j

(G) равно числу маршрутов из i в j длины

k, где t является предпоследней вершиной. Просуммировав в формуле

(*) это произведение по всем возможным промежуточным вершинам t, мы получим число всех маршрутов из i в j длины k, что и требовалось доказать.

D

Пример 4.6.3 . Продолжим пример 4.6.1. Рассмотрим квадрат матрицы смежности графа с рисунка 43.

₀

₁

A²(G) = ^0

₁₂

1	0	0
0	1	0
1	0	1
0	1	0

₁

0

^2 1 1 0 1^

^1 3 0 1 1^

= 1 0 2 0 1 .

   

   

_{0 0}

^0 1 0 1 0^

1 1 0 0 0

1 1 1 0 2

Глядя на рисунок можно убедиться, что что на диагонали стоят степени соответствующих вершин. Это логично, так как маршрут из вершины i в нее же длины 2 является проходом по по каждому ребру графа смежному с i туда и обратно. Остальные элементы матрицы равны 1 в тех случаях, если между соответствующими вершинами есть цепь длины 2.

Замечание 4.6.2 . Можно заметить, что изоморфным графам могут соответствовать разные матрицы смежности. Но это различие не произвольно. Изоморфные графы по сути отличаются порядком нумерации вершин. Этому порядку соответствует порядок нумерации строк и столбцов матрицы смежности. Таким образом матрицы смежности для изоморфных графов отличаются друг от друга одинаковой перестановкой строк и столбцов.