6. Алгоритмически неразрешимые задачи

В силу интуитивности понятия алгоритма, вопрос о существовании алгоритмического решения некоторого класса задач оставался без ответа. Избавиться от неопределенности позволил тезис Тьюринга-Черча, который устанавливает соответствие между интуитивным понятием алгоритмически разрешимой задачи и понятием машины Тьюринга, которое возможно изучать с формально-математической точки зрения.

Тезис Тьюринга-Чёрча: Любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной Тьюринга.

Физический тезис Тьюринга-Чёрча: Любая функция, которая может быть вычислена физическим устройством, может быть вычислена машиной Тьюринга.

Этот тезис позволяет нам четко определить алгоритмически неразрешимую проблему, как проблему, для которой не существует решающей ее машины Тьюринга. Из теоремы 3.1.1 следует, что существуют функции, которые нельзя вычислиь с помощью машин Тьюринга, а значит алгоритмически неразрешимые задачи существуют. Далее в этом параграфе приведем пример такой функции.

Определим функцию "Продуктивность" следующим образом:

⁽ f_M (0), f_M (0) - определена,

Продуктивность(M ) =

0, иначе .

Пример 3.1.3 . Машина Тьюринга на рисунке 21 имеет продуктивность 2, поскольку запущенная на пустой ленте она рисует две единички и останавливается. Машина Тьюринга на рисунке

:1 ^:1

_q 1:L _q

¹ 2

Рисунок 21: Машина с двумя состояниями и продуктивностью 2

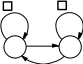
22, запущенная на пустой ленте, не останавливается, а рисует бесконечную последовательность единиц. Ее продуктивность - 0.

:1 ^:1

_q 1:L _q

¹ 1:L ²

Рисунок 22: Машина с двумя состояниями и продуктивностью 0

Определение 3.1.12 . Введем функцию максимальной продуктивности машины Тьюринга с n состояниями.

p(n) = max

M – м.Т. с n состояниями

Продуктивность(M ), n ∈ N.

Чтобы получить функцию N₀ → N₀, доопределим функцию p в нуле:

p(0) = 0.

Лемма 3.1.2 (о свойствах фукнции p(n)). Пусть n ∈ N₀. Тогда

1) p(n + 1) > p(n) (монотонность), 2) p(n + 9) ≥ 2n.

Доказательство. 1) Пусть M - такая машина Тьюринга с n

состояниями, что Продуктивность(M ) = p(n). Построим машину M ^t

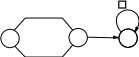
на основе машины M согласно рисунку 23, добавляя к машине одно состояние и увеличивая продуктивность на единицу. M (Λ) = Dq_n 1...1 D,

p (n )

:1

q M ^q

1:L _q

1 ^{n n+1}

Рисунок 23: Машина M ^!

а машина M ^t содержит дополнительное состояние и две новые команды q_n1 → q_n+1L и q_n+1D → q_n+11 которые сдвигают головку на

одну ячейку влево и дорисовывают дополнительную единицу, так что

M ^t(Λ) = Dq_n+1 1...1

p (n ) + 1

D. Мы получили машину Тьюринга M ^t с n + 1

состоянием и продуктивностью p(n) + 1. Следовательно

p(n + 1) ≥ Продуктивность(M ^t) = p(n) + 1 > p(n).

2) Построим машину M ^tt на основе машин M_n из примера 3.1.1 и M_×2

из примера 3.1.2 согласно рисунку 24: машина M_n рисует n единиц а

машина M_×2 удваетвает это число. Поскольку у машины M_n n состояний, а у M_×2 - 9 состояний, то у машины M ^tt n + 9 состояний. Таким образом, M ^tt(Λ) = Dq_n+9 1...1 D. Тогда

2n

q₁ M_n

1:1

_n q

q

n+1

^Mx2

^qn+9

Рисунок 24: Машина M ^!!

p(n + 9) ≥ Продуктивность(M ^tt) = 2n.

D

Теорема 3.1.3 (об алгоритмической неразрешимости задачи вычисления функции p(n)). Не существует машины Тьюринга

T , для которой f_T (n) = p(n) для всех n ∈ N₀.

Доказательство. Пусть такая машина T существует и пусть у нее k состояний. Построим машину M с n + 2k состояниями таким образом, чтобы ее продуктивность была равна p(p(n)):

M (Λ) = Dq_n+2k 1...1 D.

p (p ( n ))

Машина M получается путем соединения машины M_n с n состояниями из примера 3.1.1 с двумя копиями машины T (рис. 25); всего у машины M n + 2k состояний. Проверим, что продуктивность такой машины p(p(n)). Сначала на пустом слове работает машина M_n и рисует на ленте n единичек:

M_n(Λ) = Dq_n 1...1 D.

n

Затем работает копия машины T с состояниями q_n+1, ..., q_n+k. Получая в качестве аргумента n, машина вычисляет функцию p(n):

T (D 1...1 D) = Dq_n+k 1...1 D.

n

p (n )

^{q M}n

_q 1:1 _q

^{T q 1:1} q T ^q

^{1 n n+1 n+k} n+k+1 ^n+2k

Рисунок 25: Машина с продуктивностью p(p(n))

Последней работает копия машины T с состояниями q_n+k+1, ..., q_n+2k, вычисляя максимальную продуктивность от своего аргумента:

T (Dq_n+k 1...1 D) = Dq_n+2k 1...1 D.

p (n )

p (p ( n ))

Следовательно, искомая машина M построена.

По построению, у машины M n + 2k состояний. Следовательно,

p(p(n)) = Продуктивность(M ) ≤ p(n + 2k).

Тогда, p(n) ≤ n + 2k по первому пункту леммы 3.1.2. Так как последнее неравенство верно для любого натурального n, то оно верно и для n + 9:

p(n + 9) ≤ n + 2k + 9. Из второго пункта леммы 3.1.2 следует, что

2n ≤ p(n + 9) ≤ n + 2k + 9.

Следовательно, n ≤ 2k + 9, что противоречит произвольности выбора номера n, так как 2k + 9 заведомо известная константа. Противоречие доказывает невозможность существования машины Тьюринга T ,

вычисляющей функцию максимальной продуктивности.

D

Задача 3.1.1 (проблема остановки машины Тьюринга). Пусть N (M ) - номер машины Тьюринга M согласно нумерации, использованной в доказательстве утверждения 3.1.1. Существует ли такая машина Тьюринга M_s, что для любой машины Тьюринга M

⁽ Dq1D, M (Λ) - определено,

M_s(1...1) =

N (M )

DqD, M (Λ) - неопределено.

Следствие 3.1.4 . Проблема остановки машины Тьюринга алгоритмически неразрешима.

Доказательство этого факта основывается на теореме 3.1.3. Его идея сводится к тому, что если бы существовала машина, способная определить остановится ли произвольная машина Тьюринга, нам удалось бы построить и машину Тьюринга, вычисляющую максимальную продуктивность машины Тьюринга с n состояниями.

Смысл алгоритмической неразрешимости проблемы остановки машины Тьюринга состоит в том, что не может существовать алгоритма, который, получая на вход описание произвольного алгоритма, мог бы определить, завершит ли последний работу за конечное время, или его выполнение будет зациклино.

Можно привести другие примеры. Например, алгоритмически неразрешимой является задача о выводимости формулы в исчислении предикатов.

Задача 3.1.2 . Пусть A - формула исчисления предикатов. Выводима ли A в исчислении предикатов?

2. Теория N P -полных задач