3. Способы записи машины Тьюринга

Для однозначного определения машины Тьюринга достаточно задать ее программу. Действительно, если мы сравним две машины с одинаковой

программой, то окажется, что они могут отличаться только элементами из множеств A и Q какой-то из машин, которые не используются ни в одной из команд. В таком случае, это символы алфавита, на которые данная машина никак (за исключением остановки) не отреагирует, или состояния, в которые она никогда не перейдет. С точки зрения обработки входных данных, между такими машинами не будет никакой разницы.

Прямой записью машины Тьюринга будет простое перечисление команд программы через запятую или в столбец, как мы это сделали в примере 3.1.1. Этот способ не очень удобен для понимания структуры программы и поиска нужной команды.

Более удобным представлением может оказаться таблица (n + 1) × k,

в которой по вертикали перечисляются символы из A ∪ {D}, а по

горизонтали состояния машины. В ячейке в строке, соответствующей

символу a, и столбце, соответствующем состоянию q_i записывается q_j b, если в программе данной машины есть команда q_ia → q_j b.

Например, таблица для программы из примера 3.1.1 будет выглядеть следующим образом:

	q1 q2	q3
D 1	q11 q21 q2L q3L	q31

При этом представлении гораздо проще быстро определить, какая команда должна выполняться в следующий момент. Кроме того, из таблицы очевидно, машина может остановиться в том и только в том случае, если она в какой-то момент окажется в состоянии q₃ и ее головка будет обозревать символ 1.

Наиболее точно представляет структуру работы машины Тьюринга граф переходов. Граф переходов для машины из примера 3.1.1 представлен на рисунке 18. Каждая вершина такого графа соответствует одному из состояний машины Тьюринга, а каждая стрелка - команде программы этой машины.

Например, команде q₁D → q₁1 соответствует стрелка от вершины q₁

к ней же самой, а над стрелкой указана замена символа D на символ 1: "D : 1"; команде q₁1 → q₂L соответствует стрелка от вершины q₁ к

вершине q₂ с пометкой "1 : L".

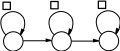:1 ^{:1 :1}

_q 1:L _q

1:L _q

¹ 2 ³

Рисунок 18: Граф переходов машины M₃

4. Стандартные конфигурации

Пусть M - машина Тьюринга с алфавитом A и множеством состояний

Q.

Определение 3.1.2 . Пусть ..., γ₋₃, γ₋₂, γ₋₁, γ₀, γ₁, γ₂, γ₃, ... - символы на ленте M .

Пусть существуют i, j : i ≤ j, γ_i, γ_j ∈ A, и γ_k = D, при k < i или

k > j. Тогда γ = γ_i, γ_i+1, ..., γ_j - слово на ленте машины M .

Если для любых i имеем γ_i = D, то говорят, что на ленте записано пустое слово: γ = Λ.

Определение 3.1.3 . Расширением слова на ленте называется запись δγσ, где γ - слово на ленте, δ и σ слова конечной или нулевой длины из символа D.

Определение 3.1.4 . Конфигурация, в которой находится машина Тьюринга в определенный момент времени, может быть представлена записью вида

τ_k, τ_k+1, ..., τ_l−1, q, τ_l, ..., τ_m,

где τ_k, τ_k+1, ..., τ_m - расширение слова на ленте, q - состояние, в котором находится машина M , а l - номер ячейки, которую обозревает головка машины.

Определение 3.1.5 . Стандартная начальная конфигурация имеет вид Dq₁αD, где α - слово на ленте.

Определение 3.1.6 . Стандартная конечная конфигурация имеет вид DqβD, где q ∈ Q, β - слово на ленте; β = Λ или β = β_i, ..., β_j , β_s /= D, при i ≤ s ≤ j.

Определение 3.1.7 . Длина слова на ленте γ -

⁽ j − i + 1, γ = γ_i, ..., γ_j ,

L(γ) =

0, γ = Λ.

Определение 3.1.8 . Пусть, M - машина Тьюринга. M (α)

- конфигурация, в которой останавливается машина Тьюринга M , запущенная из стандартной начальной конфигурации Dq₁αD.

M (α) неопределена, если M не остановится.

Определение 3.1.9 . Говорят, что машина Тьюринга M принимает слово α, если M (α) - стандартная конечная конфигурация.