1. Элементы теории множеств. Комбинаторика.

1. Введение

Понятие "дискретная математика" объединяет все разделы математики, которые работают с дискретными структурами. Конечно, между ними есть взаимосвязи, местами они ссылаются друг на друга, но все вместе это является единой теорией в той же степени, в какой единой является и вся математика в целом. Это совокупность самостоятельных теорий и направлений.

Теория множеств и комбинаторика содержат базу, которые используются во многих других разделах математики (в том числе и дискретной).

Теория алгоритмов занимается формализацией понятия алгоритма, изучением его закономерностей и свойств. Много внимания уделяется оценке сложности алгоритмов и их сравнению.

Теория графов изучает один из видов дискретных структур - графы. В силу своей интуитивной понятности и наглядному визуальному представлению, графы очень часто используются в качестве моделей для структур самой разной природы.

Математическая логика изучает фундаметальные структуры, которые лежат в основе правильных математических рассуждений.

Дискретная математика содержит и много других подразделов, которые не вошли в рамки этого ознакомительного курса.

2. Примеры задач.

На первом занятии познакомимся с примерами задач, которые входят в рассмотрение дискретной математики.

1. Задача о расположении конвертов

Рассмотрим задачу, для решения которой не потребуется знания специальной теории. Многие достаточно подготовленные читатели могут еще в процессе рассуждений догадаться, каков ответ на задачу, но мы все-таки пройдем все стадии, чтобы лучше понять сам процесс решения.

Задача 1.2.1 . Имеется n квадратных конвертов разного размера (нет двух одинаковых конвертов). Все конверты находятся в ящике, причем одни конверты можно вкладывать в другие. Сколько существует способов размещения конвертов в ящике без учета их пространственного положения?

Пример 1.2.1 . Пусть имеется три конверта размера l₁, l₂ и l₃, причем 0 < l₃ < l₂ < l₁. На рисунке 1 изображены все возможные

¹ 2 3

4 ^{5 6}

Рисунок 1: Все возможные относительные расположения трех конвертов в ящике

расположения трех конвертов. Всего их оказывается шесть.

Русский язык, как и любой другой разговорный язык, допускает различные понимания одной и той же последовательности слов (символов). Этим он плох для формулировки задачи. Необходимо поставить задачу формально (строго).

Пусть 0 - ящик. Упорядочим конверты по убыванию размера и сопоставим 1 самому большому конверту, 2 - следующему и так далее. Самый маленький конверт получит номер n. Тогда любому размещению

конвертов в ящике можно сопоставить пару (n, A), где n ∈ N - число

конвертов, а A некоторое множество пар (i, j), i ∈ N₀ = N ∪ {0},

j ∈ N, i, j ≤ n. Если (i, j) ∈ A, то конверт j при нашем размещении

непосредственно вложен в конверт i.

Пример 1.2.2 . Например размещению 2 на рисунке 1 соответствует множество A = {(0, 1), (1, 2), (2, 3)}, а размещению 6 того же рисунка

- множество A = {(0, 1), (0, 2), (2, 3)}.

Не любому множеству пар A соответствует некоторое размещение конвертов. Введем дополнительные ограничения на A:

1. i ∈ N, i ≤ n ⇒ |{(k, i) : (k, i) ∈ A}| = 1 - любой конверт

непосредственно вложен ровно в один другой конверт или ящик.

2. (i, j) ∈ A ⇒ i < j - меньший конверт вкладывается в больший.

Задача 1.2.2 . Найти функцию натурального аргумента n ∈ N

f (n) = |{A : A ⊆ {0, 1, ..., n − 1} × {1, 2, ..., n},

A удовлетворяет условиям 1) и 2)}|

Итак, мы сформулировали строгую постановку задачи и знаем, что нам нужно найти. Тем не менее ответить на поставленный вопрос сразу не так просто. Даже если мы угадаем ответ сейчас, его доказательство может оказаться достаточно сложным для понимания. Чтобы избежать необходимости непосредственно выяснять количество возможных пар (n, A), сопоставим каждой такой паре графическое изображение - возрастающее дерево.

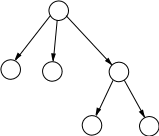
Пример 1.2.3 . Пусть у нас есть некоторое расположение (n, A) = (5, {(0, 1), (0, 2), (0, 4), (1, 3), (1, 5)}). Сопоставим ему возрастающее

дерево (рис. 2): {0, 1, 2, 3, 4, 5} - множество вершин (узлов), 0 -

корень, стрелки - ориентированные ребра (дуги), 1 - внутренний узел,

2, 3, 4, 5 - листья. Узел 0 называют родительским (или отцом) для

узлов 1, 2 и 4, которые называют детьми (сыновьями) узла 0. Узел 1 в свою очередь является отцом узлов 3 и 5.

0

4 _{2 1}

5 ₃

Рисунок 2: Пример возрастающего дерева

Особенности возрастающих деревьев: 1) В любой узел из корня можно попасть двигаясь по стрелкам и притом единственным образом; 2) при движении от корня по стрелкам номера узлов только возрастают.

Формально возрастающее дерево можно определить следующим образом:

Определение 1.2.1 . 1) Пусть x - некоторый узел, помеченный числом n_x. Тогда можно говорить, что x возрастающее дерево, состоящее из одного узла, и узел x является корнем этого дерева.

2) Пусть x - некоторый узел, помеченный числом n_x, и T₁, T₂,..., T_k

- возрастающие деревья с корнями соответственно x₁, x₂, ..., x_k; узел x_i помечен числом n_xi , i = 1, k. Если n_x < n_xi для любого i = 1, k, то можно построить возрастающее дерево x(T₁, T₂, ..., T_k) с корнем x и поддеревьями T₁, T₂,..., T_k.

Пример 1.2.4 . Возрастающее дерево с рисунка 2 можно записать

0(4, 2, 1(5, 3)).

Нетрудно видеть, что любому возрастающему дереву T с узлами

{0, 1, ..., n} соответствует некоторое размещение n конвертов (n, A), где

A состоит из пар (i, j) соединенных в дереве T стрелкой из i в j. Верно

и обратное: по размещению конвертов можно построить возрастающее дерево, как это сделано в примере 1.2.3.

Таким образом, наша задача эквивалентна следующей:

Задача 1.2.3 . Найти число возрастающих деревьев с n вершинами.

Для определенности будем считать, что все дети одного родительского узла расположены в графическом изображении возрастающего дерева по убыванию слева направо. Так на рисунке 2 вершины 4, 2 и 1 могли бы быть изображены в другом порядке, структура дерева бы не изменилась. Чтобы не путать разные изображения одного дерева, вводим это ограничение.

Рассмотрим еще один способ описания возрастающего дерева - последовательность из n + 1 различных элементов из множества

{0, 1, ..., n}.

Определение 1.2.2 . Назовем перестановкой чисел {1, 2, ..., n} произвольную упорядоченную последовательность π из n различных чисел 1, 2, ..., n:

π ∈ {(k₁, k₂, ..., k_n) | k_i ∈ {1, 2, ..., n}, i = 1, n; k_i /= k_j , при i /= j}

Рассмотрим слово τ начинающееся с 0 и продолжающееся некоторой перестановкой чисел {1, 2, ..., n}: τ = (0, k₁, k₂, ..., k_n).

Пример 1.2.5 . Пусть τ = (0, 4, 2, 1, 5, 3). Строим по τ возрастающее дерево T . Каждое число в τ - узел дерева T ; 0 - корень.

Пусть i /= 0 - элемент τ . Пусть j ближайший к i слева элемент

τ , такой что j < i. Тогда j - отец узла i. Нетрудно убедиться, что

полученное таким образом по τ дерево T совпадает с деревом на рисунке 2.

Итак, чтобы получить по некоторому возрастающему дереву T

соответствующее слово τ , нужно каждому листу i сопоставить запись

τ_i = i, а каждому родительскому узлу j с детьми i₁, i₂, ..., i_k, i₁ ≥ i₂ ≥

... ≥ i_k, сопоставить запись:

τ_j = j, τ_i1 , τ_i2 , ..., τ_ik ,

где τ_il - запись для узла i_l.

Нетрудно видеть, что, поскольку номер любого сына больше номера

родительского узла, а номера узлов i₁, i₂, ..., i_k, упорядочены по убыванию, то просматривая список влево от любого i_l мы правильно определим его родителя - j. Тогда τ = τ₀ и есть искомое представление дереваT.

Пример 1.2.6 . Построим указанным способом слово τ для возрастающего дерева на рисунке 2. Считаем записи для листьев: τ₃ = 3, τ₅ = 5, τ₂ = 2, τ₄ = 4. Теперь можно получить записи для родительских узлов: τ₁ = 1, τ₅, τ₃ = 1, 5, 3, τ₀ = 0, τ₄, τ₂, τ₁ = 0, 4, 2, 1, 5, 3.

Мы получили, что τ = (0, 4, 2, 1, 5, 3), что соответствует слову τ из

примера 1.2.5.

Таким образом, по дереву T мы однозначно строим слово τ , состоящее из нуля с последующей перестоновкой чисел {1, 2, ..., n}. С

другой стороны по слову τ однозначно восстанавливается дерево T способом, описанным в примере 1.2.5. Этим мы показали, что каждому возрастающему дереву T взаимнооднозначно соответствует некоторая

перестановка чисел {1, 2, ..., n}, а наша задача сводится к следующей:

Задача 1.2.4 . Найти число переставновок чисел {1, 2, ..., n}.

Последнее число равно n!, что нетрудно доказать, например, по индукции.

Итак, на примере задачи о расположении конвертов мы разобрали следующие стадии решения задачи:

1. формулировка задачи из предметной области;

2. формализация условий задачи и построение математической модели;

3. последовательное сведение исходной задачи к вспомогательным задачам;

4. получение ответа путем решения вспомогательной задачи.