4. Специальные бинарные отношения: Отношение порядка

Определение 1.4.9 . Бинарное отношение ρ на множестве X называется отношением порядка, если оно транзитивно и антисимметрично. Множество, на котором введено отношение порядка, называют упорядоченным.

Пример 1.4.6 . Множество всех пар (x, y) людей, для которых x

старше y, является отношением порядка.

Определение 1.4.10 . Отношение порядка -< называется отношением нестрогого (частичного) порядка на множестве X, если оно рефлексивно.

Отношение порядка ≺ называется отношением строгого порядка на

множестве X, если оно иррефлексивно:

∀x, y ∈ X : x ≺ y ⇒ x /= y.

Определение 1.4.11 . Отношение порядка ρ на множестве X называется отношением линейного порядка, если любые x, y ∈ X, x /= y, сравнимы в смысле отношения ρ (либо xρy, либо yρx обязательно

выполняется).

Пример 1.4.7 . 1) Отношение родитель-ребенок (рисунок 6-a)) не является отношением порядка. Очевидно, что у такого отношения отсутствует транзитивность: дед не является родителем своего внука.

С другой стороны, отношение предок-потомок является отношением порядка. На рисунке 6-b) представлено то же фамильное дерево, что и на рисунке 6-a), но с указанием всех связей от дедов к внукам.

Отношение предок-потомок является отношением строгого порядка и не является линейным порядком.

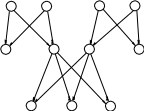
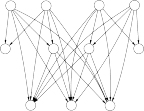
1. b)

Рисунок 6: Генеалогическое древо

2. ρ_> = {(x, y) | x, y ∈ R, x > y} - является отношением строгого

линейного порядка.

2. ρ_≥ = {(x, y) | x, y ∈ R, x ≥ y} - является отношением нестрогого

линейного порядка.

2. Отношение A ⊆ B всех пар подмножеств (A, B) заданного

универсального множества U , таких что A является подмножеством

множества B называют отношением включения. Отношение включения является отношением нестрогого порядка и не является отношением линейного порядка.

Определение 1.4.12 . Пусть на множестве X введено отношение строгого порядка ≺. Пусть элемент x ∈ X таков, что

∀y ∈ X, y /= x ⇒ x ≺ y.

Тогда элемент x называют наименьшим.

Лемма 1.4.9 . Если на конечном непустом множестве X задан линейный строгий порядок, то существует наименьший элемент, и он единственен.

Доказательство. Самостоятельно.

D

Теорема 1.4.10 . Пусть на конечном непустом множестве X задано отношение линейного строгого порядка ≺. Тогда на X можно выбрать такую нумерацию элементов X = {x₁, x₂, ..., x_n}, что соотношение x_i ≺

x_j будет выполняться в том и только в том случае, когда i < j.

Доказательство. Согласно лемме 1.4.9 для множества X существует наименьший элемент x₁ ∈ X, такой что x₁ ≺ y для любых y ∈ X. Удалим

элемент x₁ из множества X.

Множество X \ {x₁} также удовлетворяет условиям леммы 1.4.9 и,

значит, в нем тоже существует наименьший элемент - x₂.

Мы можем повторять этот процесс до тех пор, пока в множестве X

не закончатся элементы. Очевидно, по способу выбора элементов x_i,

{x₁, x₂, ..., x_n} и есть искомая нумерация.

D

Определение 1.4.13 . Два нестрого упорядоченных множества X и Y называются изоморфными, если существует биекция ϕ : X → Y , сохраняющая отношение нестрогого порядка. Иными словами, если -<_x и -<_y отношения нестрогого порядка соответственно множеств X и

Y , то

x₁ -<_x x₂ ⇐⇒ ϕ(x₁) -<_y ϕ(x₂).

Пример 1.4.8 . Рассмотрим множество 2^A всех подмножеств множества A = {1, 2, 3}, упорядоченное отношением включения, и множество X = {1, 2, 3, 5, 6, 10, 15, 30}, упорядоченное отношением

x -< y ⇔ y делится на x.

Из рисунка 7 хорошо видно, что эти два упорядоченных множества изоморфны.

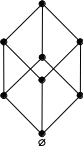
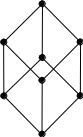^{1,2,3} 30

{2,3}

{1,2}

{1,3}

15 ₁₀

6

{2}

{3}

5

{1} ^{3 2}

1

1. b)

Рисунок 7: Изоморфные нестрого упорядоченные множества

Теорема 1.4.11 . Всякое нестрого упорядоченное множество X изоморфно некоторой системе подмножеств множества X, нестрого упорядоченной отношением включения.

Доказательство. Пусть -< - отношение нестрогого порядка на множестве X. Для каждого элемента a ∈ X рассмотрим множество S_a = {x ∈ X | x -< a}. Ясно, что S_a ⊆ X для любого a ∈ X. Покажем, что система подмножеств {S_a | a ∈ X}, упорядоченная отношением

включения, есть искомая система подмножеств. Рассмотрим отображение

ϕ : X → {S_a | a ∈ X}

такое, что ϕ(a) = S_a. Если S_a = S_b, то, поскольку a ∈ S_a, то b ∈ S_a и, следовательно, b -< a. Аналогично a -< b. Таким образом, в силу антисимметричности отношения -<, a = b. Значит, отображение ϕ

инъективно. С другой стороны, у любого множества S_a есть прообраз

a. Значит, ϕ сюрьективно. Следовательно ϕ - биекция.

Пусть a -< b. Тогда из x -< a в силу транзитивности отношения следует x -< b, а значит S_a ⊆ S_b. Пусть S_a ⊆ S_b. Тогда, поскольку a ∈ S_a, то a ∈ S_b и, следовательно, a -< b. Таким образом биекция ϕ сохраняет

отношение нестрогого порядка.

D