
- •1. Информация о дисциплине
- •1.1. Предисловие
- •1.2. Содержание дисциплины и виды учебной работы
- •1.2.1. Объем дисциплины «Финансовая математика» и виды учебной работы
- •1.2.2. Перечень видов практических занятий и видов контроля
- •2. Рабочие учебные материалы
- •2.1. Рабочая программа (объем дисциплины 150 часов)
- •Раздел 1. Наращение и дисконтирование денежных сумм (38 часов)
- •Раздел 2. Потоки платежей (25 часов)
- •Раздел 3. Некоторые схемы погашения кредитов. Оценки инвестиционных проектов (25 часов)
- •Раздел 4. Облигации (24 часов)
- •Раздел 5. Финансовые операции в условиях неопределенности (23 часа)
- •Раздел 6. Статистические характеристики. Элементы технического анализа и моделирование цены акции (13 часов)
- •2.2. Тематический план дисциплины «Финансовая математика»
- •2.2.1. Тематический план дисциплины для студентов очной формы обучения
- •2.2.2. Тематический план дисциплины для студентов очно-заочной формы обучения
- •2.2.3. Тематический план дисциплины для студентов заочной формы обучения
- •2 Классическая финансовая математика Анализ финансового рынка .3. Структурно-логическая схема дисциплины «Финансовая математика»
- •Раздел 1. Наращение и дисконтирование денежных сумм
- •Раздел 3. Некоторые схе-мы погашения кредитов
- •Раздел 2. Потоки платежей
- •Раздел 6.
- •Раздел 5. Финансовые операции в условиях неопределенности
- •2.4. Практический блок
- •2.4.1. Лабораторный практикум (очная форма обучения)
- •2.4.2. Лабораторный практикум (очно-заочная форма обучения)
- •2.4.3. Лабораторный практикум (заочная форма обучения)
- •2.5. Временной график изучения дисциплины
- •2.6. Рейтинговая система
- •3. Иформационные ресурсы дисциплины
- •3.1. Библиографический список
- •3.2. Опорный конспект по дисциплине введение
- •Раздел 1. Наращение и дисконтирование денежных сумм
- •1.1. Наращение денежных сумм
- •1.1.1 Проценты и процентные ставки
- •Пример 1.1.1
- •Решение
- •1.1.2. Наращение по простой процентной ставке
- •Пример 1.1.2
- •Решение
- •1.1.3. Наращение по сложной процентной ставке
- •Пример 1.1.3
- •Решение
- •1.1.4. Переменные процентные ставки
- •Пример 1.1.4
- •Решение
- •1.2. Дисконтирование денежных сумм
- •1.2.1. Дисконтирование по простой процентной ставке
- •1.2.2. Дисконтирование по сложной процентной ставке
- •Пример 1.2.1
- •Решение
- •1.2.3. Непрерывное дисконтирование
- •1.2.4. Банковский учет
- •Пример 1.2.2
- •Решение
- •1.3. Производные процентные расчеты
- •1.3.1. Номинальная и эффективная ставки
- •1.3.2. Эквивалентность денежных сумм
- •Пример 1.3.3
- •Решение
- •1.4. Начисление процентов с учетом налогов
- •1.4.1. Рассмотрим схему начисления простых процентов
- •1.4.2. Рассмотрим схему начисления сложных процентов
- •Пример 1.4.1
- •Решение
- •1.5. Начисление процентов с учетом инфляции
- •1.5.1. Темп инфляции
- •1.5.2. Наращение с учетом инфляции
- •1.5.3. Брутто-ставка
- •1.5.4. Реальная ставка процентов
- •Вопросы для самопроверки
- •Раздел 2. Потоки платежей
- •2.1. Финансовые ренты
- •2.2. Будущая стоимость ренты
- •2.2.1 Наращенная сумма годовой ренты постнумерандо
- •2.2.2. Наращенная сумма годовой ренты пренумерандо
- •2.2.3. Наращенная сумма годовой ренты с начальным взносом
- •Пример 2.2.1
- •Решение
- •2.3. Формула наращенной суммы постоянной p-срочной ренты
- •2.3.1. Формула наращенной суммы, в которой начисление процентов и поступления платежей совпадают по времени
- •Пример 2.3.1
- •Решение
- •2.3.2. Формула наращенной суммы, в которой начисление процентов и поступления платежей не совпадают по времени
- •Пример 2.3.2
- •Решение
- •2.4. Современная стоимость ренты
- •2.4.1. Современная стоимость годовой ренты постнумерандо
- •2.4.2. Современная стоимость годовой ренты пренумерандо
- •Пример 2.4.1
- •Решение
- •2.4.3. Современная стоимость ренты с взносом в конце срока
- •Пример 2.4.2
- •Решение
- •2.4.4. Формула современной стоимости постоянной p-срочной ренты
- •2.5. Определение величины платежа ренты
- •2.5.1. Определение величины платежа ренты, когда известна будущая стоимость ренты
- •Пример 2.5.1
- •Решение
- •2.5.2. Определение величины платежа ренты, когда известна современная стоимость ренты
- •Пример 2.5.2
- •Решение
- •Вопросы для самопроверки
- •Раздел 3. Некоторые схемы погашения кредитов Оценки инвестиционных проектов
- •3.1. Погашение кредита равными платежами
- •3.1.1. Определение размера платежа
- •Пример 3.1.1
- •Решение
- •3.1.2. Разделение платежей на части
- •Пример 3.1.2
- •Решение
- •3.2. Правило торговца
- •Пример 3.2.1
- •Решение
- •3.3. Чистая приведенная стоимость
- •Пример 3.3.1
- •Решение
- •3.4. Внутренняя ставка дохода
- •Пример 3.4.1
- •Решение
- •3.5. Срок окупаемости
- •Пример 3.5.1
- •Решение
- •Вопросы для самопроверки
- •Раздел 4. Облигации
- •4.1. Цена облигации
- •4.1.1. Цена облигации с выкупом в конце срока
- •Пример 4.1.1
- •Решение
- •4.1.2. Цена бескупонной облигации
- •4.2. Курс облигации
- •Пример 4.2.1
- •Решение
- •4.3. Доходность облигации
- •4.3.1. Доходность облигации с выкупом в конце срока
- •Пример 4.3.1
- •Решение
- •4.3.2. Доходность облигации с нулевым купоном
- •Пример 4.3.2
- •4.4. Дюрация
- •4.4.1. Дюрация по Маколею
- •Пример 4.4.1
- •Решение
- •4.4.2. Волатильность цены. Модифицированная дюрация
- •Пример 4.4.2
- •Решение
- •Вопросы для самопроверки
- •Раздел 5. Оценки финансовых операций в условиях неопределенности
- •5.1. Оценки финансовых операций в условиях полной неопределенности
- •Пример 5.1.1
- •5.1.1. Критерий Вальда (крайнего пессимизма)
- •Пример 5.1.2
- •Решение
- •5.1.2. Критерий Сэвиджа (минимального риска)
- •Пример 5.1.3
- •Решение
- •Критерий Сэвиджа
- •Пример 5.1.4
- •Решение
- •5.2. Оценки финансовых операций в условиях частичной неопределенности
- •Пример 5.2.1
- •Решение
- •5.3. Ожидаемая доходность и риск портфеля ценных бумаг
- •Риск портфеля ценных бумаг. Диверсификация
- •5.3.1 Ожидаемая доходность портфеля ценных бумаг
- •5.3.2. Коэффициент корреляции
- •5.3.3. Риск портфеля ценных бумаг
- •5.3.4. Диверсификация портфеля
- •Пример 5.3.1
- •Решение
- •5.4. Оптимальный портфель ценных бумаг
- •5.4.1. Портфель Марковица минимального риска
- •5.4.2. Портфель минимального риска из некоррелированных бумаг
- •Пример 5.4.1
- •Решение
- •Вопросы для самопроверки
- •6. Статистические характеристики портфелей. Моделирование цены акции
- •6.1. Средняя доходность и риск финансовой операции
- •6.1.1. Средняя доходность финансовой операции равна среднему арифметическому фактических доходностей по всем n наблюдениям
- •Пример 6.1.1
- •Решение
- •6.1.2. Оценка риска финансовой операции
- •Пример 6.1.2
- •Решение
- •6.1.3. Среднегодовые доходность и риск
- •6.2. Средняя доходность и риск портфеля
- •6.2.1. Ожидаемая доходность портфеля
- •6.2.2. Выборочный коэффициент ковариации
- •6.2.3. Дисперсия и риск портфеля
- •6.2.4. Портфель Марковица минимального риска
- •Пример 6.2.1
- •Решение
- •6.3. Технический анализ цен
- •6.3.1. Ценовой тренд
- •6.3.2. Линия сопротивления
- •6.3.3. Линии поддержки
- •6.4. Модель цены акции
- •Пример 6.4.1
- •6.5. Скользящее среднее
- •Вопросы для самопроверки
- •Заключение
- •3.3. Глоссарий
- •3.4. Методические указания к выполнению лабораторных работ Работа 1. Финансовые вычисления в Excel
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •3.1. Выполнение задания 1
- •Пример 1
- •Решение
- •3.1.1. Ввод исходных данных в таблицу
- •3.1.2. Расчет доли года. Ввод комментариев
- •3.1.3. Расчет процентной ставки
- •3.2. Выполнение задания 2
- •3.2.1. Описание функции бс (будущая сумма)
- •3.2.2. Вызов функции бс
- •3.2.3. Ввод аргументов
- •3.3. Выполнение задания 3 Пример 2
- •Решение
- •3.3.1. Ввод комментариев и исходных данных
- •3.4. Выполнение задания 4
- •Пример 3
- •Решение
- •3.4.2. Использование функции бс и ввод аргументов
- •3.4.3. Расчет накопленной суммы при взносах в начале периода
- •3.5. Выполнение задания 5
- •Пример 4
- •Решение
- •3.6. Выполнение задания 6
- •Пример 5
- •Решение
- •3.6.2. Определение числа периодов в годах при начислении процентов раз в году
- •3.6.3. Определение числа периодов в годах при начислении процентов поквартально
- •3.6.4. Редактирование формулы кпер
- •3.7. Выполнение задания 7 Пример 6
- •Решение
- •Работа 2. Оценка инвестиционных проектов
- •2.2. Оценка инвестиционных проектов (ип) в общем случае
- •3. Порядок выполнения работы
- •3.1. Выполнение задания 1. Расчет будущей стоимости ип
- •3.2. Выполнение задания 2. Расчет текущей стоимости ип
- •3.3. Выполнение задания 3. Оценка ип с использованием специальных функций Excel
- •3.3.4. Расчет индекса рентабельности (рi):
- •3.4. Самостоятельная работа
- •4. Отчет по работе
- •Работа 3. Определение цены облигации
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •3.1. Порядок выполнения задания 1
- •3.2. Порядок выполнения задания 2
- •4. Отчет по работе
- •Работа 4. Определение курса облигации
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •3.1. Порядок выполнения задания 1
- •3.1. Порядок выполнения задания 2
- •4. Отчет по работе
- •Работа 5. Доходность облигации
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •3.1. Порядок выполнения задания 1
- •3.2. Порядок выполнения задания 2
- •4. Отчет по работе
- •Работа 6. Модифицированная дюрация
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Отчет по работе
- •Работа 7. Вычисления характеристик портфеля некоррелированных бумаг. Оптимальный портфель
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •3.1. Порядок выполнения задания 1
- •3.3.2. Порядок выполнения задания 2
- •3.3. Порядок выполнения задания 3
- •4. Отчет по работе
- •Работа 8. Моделирование цены акции. Сглаживание по методу скользящего среднего
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •3.1. Порядок выполнения задания 1
- •3.2. Порядок выполнения задания 2
- •4. Отчет по работе
- •4. Блок контроля освоения дисциплины
- •4.1. Задание на контрольную работу
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •4.2. Методические указания к выполнению контрольной работы
- •4.2.1. Общие методические указания
- •4.2.2. Проценты и процентные ставки
- •4.2.3. Наращение по простой процентной ставке
- •Решение
- •4.2.4. Наращение по сложной процентной ставке
- •4.2.5. Математическое дисконтирование
- •Решение
- •4.2.6. Консолидация платежей
- •4.2.6.1. Определение размера консолидированного платежа
- •Решение
- •4.2.6.2. Определение срока консолидированного платежа
- •Решение
- •4.2.7. Правило торговца
- •Решение
- •4.2.8. Анализ инвестиционных проектов
- •4.2.8.1. Чистая приведенная стоимость
- •4.2.8.2. Чистый наращенный доход
- •4.2.8.3. Индекс рентабельности
- •4.2.8.4. Срок окупаемости, внутренняя ставка дохода
- •4.2.9. Внутренняя ставка дохода
- •Решение
- •4.2.10. Эквивалентность финансовых обязательств
- •Решение
- •4.3. Блок тренировочных тестов Тест № 1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •4.3.1. Таблица правильных ответов на вопросы тренировочных тестов
- •4.4. Итоговый контроль Тест № 1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •4.5. Вопросы к зачету
- •4.5.1. Часть 1
- •4.5.2. Часть 2
- •Содержание
- •Раздел 1. Наращение и дисконтирование денежных сумм 19
- •Раздел 2. Потоки платежей 34
- •Раздел 3. Некоторые схемы погашения кредитов 43
- •Раздел 4. Облигации 49
- •Раздел 5. Оценки финансовых операций в условиях неопределенности 57
- •Финансовая математика
- •191186, Санкт-Петербург, ул. Миллионная, д. 5
Пример 1.1.2
Сумма в 700 тыс. руб. помещена в банк на депозит (хранение под проценты) на 4 года под 2 % годовых. Найти сумму в конце срока, если простые проценты начисляются:
в конце каждого года и
в конце каждого квартала.
Решение
Из условий задачи следует, что
первоначальная сумма P =700 000,
годовая процентная ставка i = 0.02,
срок ссуды n = 4.
Тогда по формуле (1.1.1) получим сумму вклада при начислении процентов в конце каждого года
S = P (1 + n i) = 700 000 (1+4 0.02 ) = 756 000 руб.
Процентные деньги I = P n i = 700 000 4 0.02 = 56 000 руб. определяют вознаграждение, получаемое вкладчиком.
Для определения суммы вклада при начислении процентов в конце каждого квартала вычислим процентную ставку за квартал
i / 4 = 0,02/4 = 0,005.
Срок депозита равен m = 4, n= 16 кварталов. Тогда по формуле (1.1.3) получим сумму вклада
S = 700 000 (1+16 0,005) = 756 000 руб.
1.1.3. Наращение по сложной процентной ставке
Расчет сумм по сложной процентной ставке заключается в том, что за каждый период процентные деньги начисляются от всей накопленной к этому моменту суммы.
Пусть срок ссуды n – целое число. Тогда по истечении срока ссуды кредитор получает сумму
S = P (1 + i) n. (1.1.4)
Если срок ссуды равен t (t – доля года), то обобщая формулу (1.1.4), сумму долга рассчитывают по формуле
S = P (1 + i)t. (1.1.5)
Коэффициент наращения в данном случае равен (1 + i)t, а процентные деньги за весь срок ссуды равны
I = [(1 + i)t - 1] P.
Пусть годовая процентная ставка равна j и начисление процентов производится m раз в году. Тогда за n лет проценты начисляются m n раз по процентной ставке j / m. Формула наращения будет иметь вид
 .
( 1.1.6)
.
( 1.1.6)
4) Непрерывное начисление процента.
Если число начислений процентов m стремится к бесконечности, то из формулы (1.1.6) получаем формулу для непрерывного начисления процентов
S = P e in.
Чтобы отличить ставку непрерывного процента от дискретной ставки j, ее называют силой роста и обозначают δ.
Пример 1.1.3
Кредит в 10 000 долларов предоставлен на два года под 12 % годовых. Найти сумму долга
1) с ежегодным начислением сложных процентов,
2) с ежеквартальным начислением сложных процентов,
3) с ежедневным начислением сложных процентов.
Решение
Для решения первой части задачи используем формулу (1.1.3). Полагаем Р = 10 000, i % = 12 %, n = 2 года, период начисления процентов – один год. Тогда сумма, возвращаемая кредитору, будет равна
S = 10 000 (1 + 0,12)2 = 10 000 (1,12)2 = 12 544.
Д
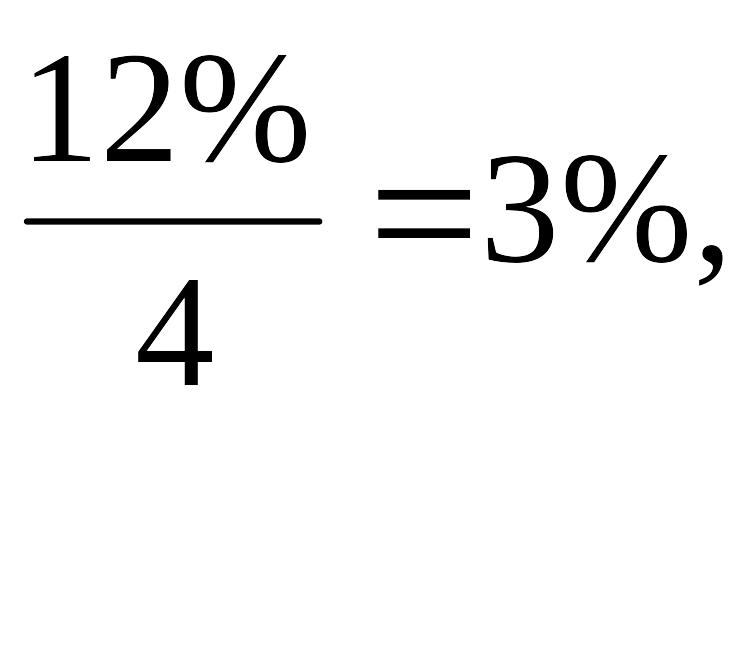
![]() число периодов начисления процентов n
m=2
4=8.
число периодов начисления процентов n
m=2
4=8.
Тогда сумма, возвращаемая кредитору, будет равна
S = 10 000 (1 + 0,03)8 = 10 000 1,26677 = 12 667,7.
Для
решения третьей части задачи сначала
используем формулу (1.3.5) cо
значением m
= 365, так
как начисление процентов производится
ежедневно. Следовательно, процентная
ставка за период (один день) равна
![]() ,
а число периодов начисления процентов
nm
= 2
365 = 730.
,
а число периодов начисления процентов
nm
= 2
365 = 730.
Тогда сумма, возвращаемая кредитору, будет равна
S = 10 000 (1 + 0,00329)730 = 12 711,99.
Теперь найдем сумму долга, используя формулу непрерывного начисления процентов
S = P e in = 10 000 e0,12·2 = 10 000 1.271249 = 12 712.49.
