Анализ модели на чувствительность

При решении задач методами линейного программирования важ­но не только найти численные значения управляемых переменных, при которых достигается оптимум, но и знать, в каком интервале

266

можно менять входные параметры без существенного отклонения от найденного оптимума и без значительного нарушения структуры бази­са, формирующего оптимальное решение. Исследование, позволяющее ответить на эти вопросы, носит название: анализ модели на чувстви­тельность. Такой анализ позволяет ответить на следующие вопросы:

Останется ли решение оптимальным, если уменьшить вклад в при­быль одной из базисных перемен?

К каким последствиям приведет сокращение объема ресурсов?

Что произойдет, если ввести в рассмотрение новую управляемую переменную?

П риемы, используемые при анализе модели на чувствительность, по своей сути весьма просты, хотя и отличаются некоторой громозд­костью. Разберемся в существе вопроса на примере, рассмотренном ранее. Запишем для этой цели исходную и «заключительную» системы уравнений, обозначим их соответственно через (Н) и (К).

(7.63)

(7.64)

где X₀ - подлежит максимизации.

Как используются выделенные ресурсы? При решении задач сво­бодные (дополнительные) переменные могут принимать следующие значения.

1. Свободная (дополнительная) переменная равна нулю. Это зна­чит, что в процессе производства используются все материалы (ре­сурсы).

2. Свободная переменная больше нуля, ресурсы используются не полностью, имеется остаток, который равен разности между запаса­ми ресурсов и израсходованными ресурсами.

3. Свободная переменная равна запасам ресурсов. Это значит, что ресурсы не используются совсем.

267

Определим, останется ли уже найденный допустимый оптималь­ный базис оптимальным, если изменить коэффициенты в выражении для целевой функции.

Для этого рассмотрим коэффициенты при небазисных перемен­ных Х₂ и Х₄ в строке 0 системы уравнений (Н). При каком значении этих коэффициентов решение останется оптимальным, а при каком становится неоптимальным?

Предположим, что коэффициент при Х₂ получает неотрицатель­ное приращение δ, т. е. становится равным 5 + δ. Тогда строка 0 систе­мы уравнений (Н) примет следующий вид:

1X₀ – 4 X₁ – (5 + δ) Х₂ – 9Х₃ –11 Х₄=0. (7.65)

При выполнении каждой симплекс-итерации мы прибавляли к строке 0 одну из остальных строк, предварительно умножив после­днюю на некоторую константу. Следовательно, на заключительной итерации строка 0 системы уравнений (К) запишется в виде

1X₀ + (3 / 7– δ)Х₂ +11/ 7Х₄ +13/ 7X₅ + 5 / 7 Х₇= 695 / 7 . (7.66)

Из полученного уравнения видно, что если δ > 3/7, то коэффици­ент при Х₂ принимает отрицательное значение. В этом случае, соглас­но правилу 1 (максимизация), в очередное базисное решение вошла бы переменная Х₂. Аналогично, если бы коэффициент при Х₄ принял значение, превышающее 11/7, то пробное базисное решение переста­ло бы быть оптимальным.

Таким образом, коэффициенты при небазисных переменных в стро­ке 0 на этапе заключительной итерации показывают, в каких преде­лах соответствующие коэффициенты в выражении для целевой фун­кции могут принимать положительные приращения без нарушения оптимальности ранее полученного базиса.

Рассмотрим, в каких пределах могут изменяться переменные, вхо­дящие в базис Х₁ и Х₃, без ущерба для оптимальности полученного решения?

Запишем строку 0 системы уравнений (Н) в виде

1Х₀ – (4 + δ) Х₁ – 5Х₂ –9 Х₃ =0 . (7.67)

В этом случае, строка 0 в (К) примет вид:

1X₀ – δХ₁ + 3 / 7Х₂ +11/ 7Х₄ +13/ 7X₅ + 5 / 7 Х₇= 695 / 7 (7.68)

Чтобы ответить на вопрос, в каких пределах можно изменять δ, не нарушая оптимальности полученного решения, необходимо об­ратить в нуль коэффициент при Х₁ в строке 0. Для этого умножим δ на строку 1 в (К) и прибавим полученный результат к полученному уравнению. Получим

268

1X₀ +(3 / 7+5 / 7 δ)Х₂ + (11 / 7 – 5 / 7 δ )Х₄ +(13 / 7 + 10 / 7 δ )Х₅ +

+(5 / 7 – 1 / 7 δ )X₇ = 695 / 7+ 50 / 7 δ . (7.69)

Из полученного уравнения следует, что при выполнении усло­вия полученное решение остается оптимальным. При б < —3/5 коэффициент при Х₂ принимает отрицательное значение. В случае, когда 8> 11/5, отрицательным становится коэффициент при X,. Таким образом, как только значение δ выходит за пределы интервала , прежний базис перестает быть опти­мальным.

Этот прием анализа пригоден не только в случае, когда изменяются коэффициенты либо при базисной, либо при небазисной переменных, по и в случае изменения нескольких коэффициентов одновременно.

Останется ли допустимым полученный оптимальный базис, если изменить значения констант в правых частях соотношений?

Рассмотрим правую часть строки 2 системы уравнений (Н). Про­изведем замену . Заметим, что свободная переменная Х₆, фигурирующая в указанной строке, входит в базис (К). Следователь­но Х₆ изменится на величину δ. Таким образом, ранее полученное решение останется допустимым, если , см. строку 2 в системе уравнений (К).

Рассмотрим правую часть уравнения в строке 1 системы уравне­ний (Н). Произведем замену . При каких значениях δ по­рученный базис остается допустимым?

Будем учитывать при выполнении симплекс-итераций произве­денную замену. На последней итерации будем иметь:

(7.70)

Обратим внимание на то, что введение δ в правую часть сопро­вождается появлением в левой части переменной Х₅.

Полагая, как обычно, небазисные переменные Х₁, Х₄, Х₅ и Х₇ равными нулю, получим значения базисных переменных, которые определяются теперь через δ. Чтобы базис оставался допустимым, константы в правых частях уравнений должны иметь неотрицатель­ные значения. Отсюда следует, что если

(7.71)

то пробное решение остается допустимым.

269

(7.76)

(7.77)

минимизировать

При значение базисной переменной Х₁ становится отрицательным; при отрицательное значение принимает базисная переменная Х₆.

Положим δ = 1, что можно интерпретировать как увеличение «ре­сурса» в строке 1 на единицу. С помощью соотношения в строке 0 системы уравнений (К) видно, что при этом значение целевой фун­кции возрастет на 13/7. Другими словами, при увеличении объема ресурсов на единицу дополнительная прибыль в оптимальном вари­анте составит 13/7.

Произведем одновременно следующие замены:

Затем после выполнения всех операций, позволяющих перейти от системы (Н) к системе (К), и обращения в нуль всех небазисных переменных, будем иметь:

(7.73)

Коэффициенты при δ_i совпадают с коэффициентами при соот­ветствующих свободных переменных в (К). Базис остается допусти­мым, если значения X₁ Х₆ и X₃ неотрицательны. Следовательно, δ₁ δ₂ и δ₃ должны удовлетворять соответствующей системе неравенств.

Двойственность задач линейного программирования

В теории линейного программирования существует понятие двой­ственности, которое позволяет унифицированным образом уста­навливать взаимосвязи для всех приемов и методов анализа моделей на чувствительность. Рассмотрим понятие «двойственность» на двух следующих задачах:

максимизировать

(7.74)

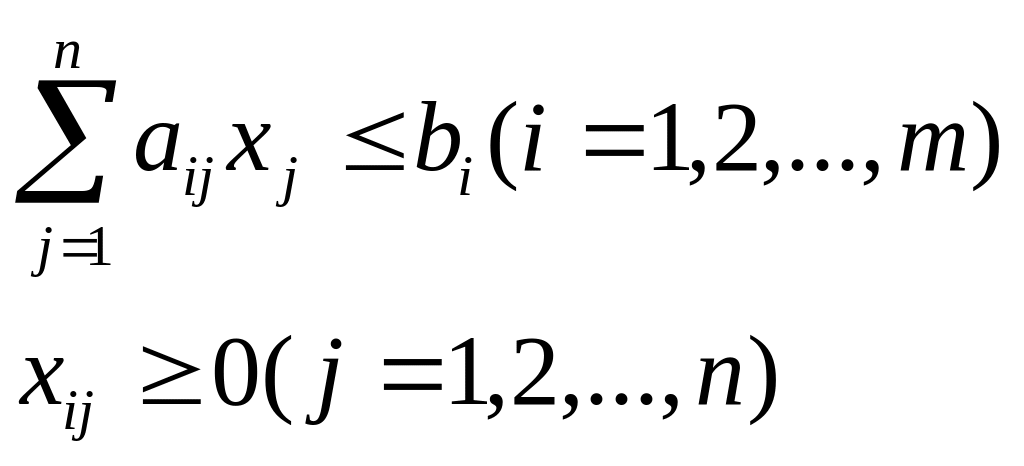
при ограничениях

п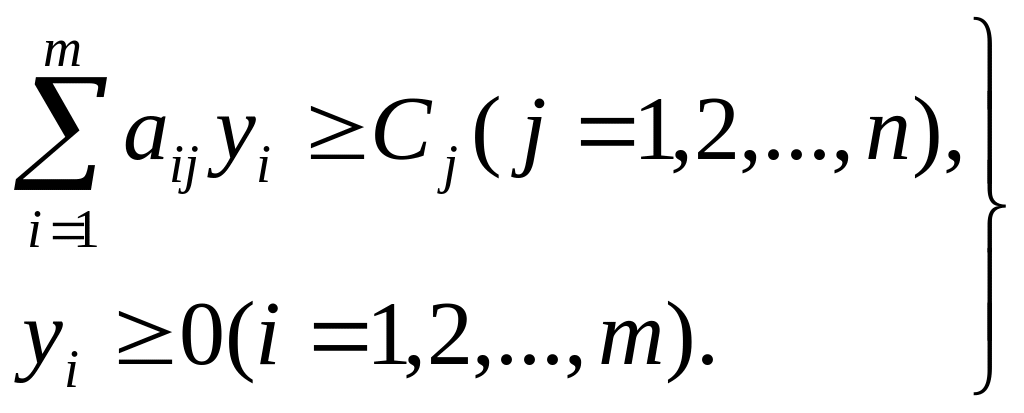 ри ограничениях

Условно назовем первую задачу исходной, а вторую двойственной (по отношению к первой). Рассмотрим это на примере. Исходная задача:

(7.72)

максимизировать

(7.78)

(7.79)

при ограничениях

(7.81)

Двойственная задача: минимизировать

(7.80)

при ограничениях

Образно говоря, двойственная задача — это на 90 градусов повер­нутая исходная задача:

1. j-й столбец, составленный из коэффициентов, фигурирующих в ограничениях исходной модели, совпадает с j-й строкой, состав­ленной из коэффициентов, фигурирующих в ограничениях двойствен­ной модели;

2. строка, составленная из коэффициентов в выражении для це­левой функции, совпадает со столбцом, составленным из констант, фигурирующих в правых частях ограничений двойственной модели;

3. столбец, составленный из констант, фигурирующих в правых частях ограничений исходной модели, совпадает со строкой, состав­ленной из коэффициентов в выражении для целевой функции двой­ственной модели;

4. (7.75)

   направление знаков неравенства в исходной модели противо­положно направлению знаков неравенства в двойственной модели. Требование максимизации в исходной задаче заменено требованием минимизации в двойственной задаче.

270

271

Теорема двойственности:

а) если исходная и двойственная ей задача имеют допустимые ре­шения, то: существует оптимальное решение X*_j(j = 1,2,...,n) исход­ ной задачи; существует оптимальное решение Y*_i (i = 1,2,...,т) двой­ственной задачи;

имеет место следующее соотношение:

(7.82)

б) если исходная (двойственная) задача допускает оптимальное решение, для которого значение целевой функции ограничено, то соответствующая ей двойственная (исходная) задача допускает опти­мальное решение при том же значении целевой функции.

Если существует допустимое решение двойственной задачи, для которого значение целевой функции совпадает со значением целевой функции исходной задачи, то решения обеих задач являются опти­мальными.

Решение двойственной задачи

В качестве примера рассмотрим ранее решенную задачу о распре­ делении ресурсов: максимизировать (7.83) (7.83)

при ограничениях (7.84) (7. 14)

Д войственная задача будет формулироваться следующим образом: минимизировать (7.85)

п ри ограничениях (7.86)

Оптимальные значения переменных двойственной задачи:

а) коэффициенты при свободных переменных в строке 0 на после­ дней симплекс-итерации при решении задачи максимизации совпа­дают с оптимальными значениями переменных двойственной задачи;

б) коэффициент при X_j в строке 0 на последней симплекс-итера­ ции представляет собой разность между левой и правой частями j-го

272

ограничения двойственной задачи, соответствующую оптимальному решению последней.

Рассмотрим коэффициенты при трех свободных переменных в стро­ке 0 на заключительной симплекс-итерации (см. формулу (7.64)). Со­гласно утверждению, приведенному выше, оптимальными значения­ми переменных двойственной задачи являются следующие:

Y₁ =13/7, Y₂= 0, Y₃ =5/7. (7.87)

Убедимся, что выполняются условия (7.82)

(7.88)

а также то, что значение целевой функции двойственной задачи со­впадает со значением целевой функции исходной задачи

(7.89)

Решение (7.83) должно быть оптимальным, поскольку удовлет­воряются все ограничения и, кроме того, значения целевых функций исходной и двойственной задач совпадают. Наконец, вычислим раз­ность между левыми и правыми частями соотношений (7.84)

(7.90)

т. е. получаем значения коэффициентов при Х₂ и Х₄ в строке 0 системы уравнений (К), что согласуется с утверждением, сформулированным выше.

Таким образом, симплексный метод можно рассматривать как способ получения пробных решений двойственной задачи путем определения допустимых решений исходной задачи. Как только удается найти допустимое решение этих двух задач, процесс итера­ции заканчивается.

Продолжение анализа на чувствительность.

(7.91)

В ыше говорилось о том, что теорема двойственности позволит луч­ше разобраться в анализе линейных моделей на чувствительность. Обращаясь к примеру, рассмотренному выше, разберем уравнение

Если коэффициент при Х₂ в выражении для целевой функции

положить равным 5 + δ, то в правой части соотношения (7.87) также

273

будет стоять 5 + δ. Подставив в (7.87) оптимальные значения двой­ственной задачи (7.83), получим (с учетом замены (5 + δ):

1 • 13 / 7 + 5• 0 + 5 • 5 / 7 5 + δ (7.92)

или

3/7 δ.

Таким образом, решение двойственной задачи остается допусти­мым, если δ не превышает 3/7. Если же δ принимает значение, превы­шающее значение 3/7, то это решение не является более допустимым и, следовательно, рассматриваемое решение исходной задачи не явля­ется более оптимальным.

В каких случаях в базис можно вводить новую переменную? Пред­положим, что в нашу задачу вводится дополнительная переменная, причем дополнения к строкам имеют следующий вид:

(7.93)

Пусть при переменной Х₈ в выражении для целевой функции стоит коэффициент C₈. При каком значении С₈ целесообразно ввес­ти в базис переменную Х₈? Соответствующее соотношение двойствен­ной задачи имеет вид:

1Y₁ + 2 / 7Y₂ + 17Y₃ С₈. (7.94)

Подставив сюда полученные оптимальные значения переменных двойственной задачи, получим

1 • 13/7 + 2/7 • 0 + 17 • 5/7 С₈. (7.95)

Значит, при С₈ 14 переменную нужно включать в базис. Опти­мальное значение каждой переменной двойственной задачи опреде­ляет положительное или отрицательное приращение значения целе­вой функции за счет единичного приращения (положительного или отрицательного) значения константы в правой части соответствую­щего ограничения при условии, что рассматриваемый базис остает­ся допустимым.

Оптимальное значение переменных двойственной задачи назы­вают скрытыми доходами. Почему в нашей задаче увеличение объема материала типа А не приводит к увеличению прибыли? Это объяс­няется тем, что запас материала типа А превышает имеющиеся в нем потребности, что видно из того обстоятельства, что свободная пере­менная Х₆ входит в оптимальный базис. Увеличение заведомо избы­точного ресурса не может увеличить прибыль.