
- •1. Грузы, измерители перевозочного процесса и тарифы
- •1.1. Грузы Классификация грузов
- •Транспортная маркировка грузов
- •1.2. Измерители процесса перевозки
- •Объем перевозок
- •Неравномерность объема перевозок
- •Грузопоток
- •Партионность перевозок
- •Транспортная продукция
- •Транспортный путь
- •Транспортное время
- •1.3. Тарифы
- •2. Автомобильные транспортные средства и показатели их использования
- •2.1. Классификация автомобилей
- •Допустимые значения осевых масс двухосных атс и двухосных колесных тележек, при превышении которых транспортное средство относится к категории 1
- •Допустимая полная масса атс, при превышении которой они относятся к категории 1
- •Допустимая полная масса атс при движении но мостовым сооружениям, превышая которую они попадают в категорию 1
- •Выброс загрязняющих веществ транспортными средствами с дизельными двигателями
- •Ограничения внешнего шума грузовых автомобилей общей массой более 3,5 т
- •2.2. Показатели использования автомобильного транспорта Парк подвижного состава
- •Провозные возможности подвижного состава
- •Себестоимость перевозки груза
- •Анализ себестоимости транспортирования
- •Значение коэффициента использования грузоподъемности автомобиля при работе с различными погрузчиками
- •3. Технология грузовых автомобильных перевозок
- •3.1. Основные принципы технологии перевозочного процесса
- •3.2. Прямые и смешанные автомобильные сообщения
- •3.3. Цикл транспортного процесса
- •Этап погрузки (разгрузки)
- •Этап транспортирования груза
- •3.4. Прогрессивные технологические процессы перевозки грузов Контейнерные перевозки
- •Основные параметры универсальных контейнеров
- •Использование площади кузовов автомобилей при их загрузке пакетами размером 800x1200 и 1000x1200
- •Комбинированные перевозки грузов
- •Перевозки грузов автомобилями-самосвалами и автопогрузчиками
- •4. Организация автомобильных перевозок
- •4.1. Основы организации перевозочного процесса Что такое организация
- •Транспортный комплекс
- •4.2. Подготовка процесса перевозки грузов
- •Экономическая подготовка
- •Техническая подготовка
- •Технологический проект перевозки
- •Организационная подготовка
- •4.3. Служба организации перевозок Функции службы организации перевозок
- •Диспетчерский доклад о выполнении суточного оперативного плана перевозок грузов
- •4.4. Передовые методы организации перевозок Централизованные перевозки грузов
- •Бригадная форма организации труда
- •Интермодальные перевозки
- •Некоммерческие перевозки
- •4.5. Особенности организации перевозок грузов
- •Особенности организации перевозок, сельскохозяйственных грузов
- •4.6. Организация междугородных и международных перевозок Междугородные перевозки
- •Международные перевозки
- •5. Управление автомобильными перевозками
- •5.1. Определение управления
- •5.2. Современное состояние управления автомобильными перевозками
- •5.3. Функции управления
- •5.4. Стадии процесса управления
- •5.5. Диспетчерское управление перевозками Основные правила построения структуры управления
- •5.6. Руководитель коллектива
- •5.7. Стимулы и наказания
- •6. Измерение эффективности перевозочного процесса
- •6.1. Показатели эффективности
- •6.2. Факторы, учитываемые при оценке эффективности перевозок
- •6.3. Оценка эффективности перевозок
- •Фактическая эффективность перевозочного процесса
- •7.2. Графоаналитический метод
- •7.3. Метод потенциалов
- •Базисный план, составленный способом северо-западного угла
- •Базисный план, составленный способом наименьшего элемента по столбцу
- •7.4. Маршрутизация перевозок
- •Рациональное закрепление потребителей за поставщиками при перевозке песка, ездок
- •Рациональное закрепление потребителей за поставщиками при перевозке щебня, ездок
- •Рациональное закрепление потребителей за поставщиками при перевозке глины, ездок
- •Рациональный план движения автомобилей из пунктов выгрузки в пункты погрузки груза, ездок
- •(Вторая итерация)
- •7.5. Применение теории массового обслуживания в организации перевозок
- •7.6. Решение задач в сетевой форме
- •7.7. Симплексный метод Общие положения
- •Итерация 1
- •Определение исходного базиса
- •Анализ модели на чувствительность
- •7.8. Сетевое планирование в управлении
- •7.9. Ситуационные игры
- •1. Сокращения
- •2. Условные обозначения
- •2.1. Расстояния (протяженность)
- •2.2. Объемы перевозок
- •2.3. Время
- •2.4. Производительность
- •2.5. Скорость
- •2.7. Стоимостные показатели
- •2.8. Числовые величины
- •2.9. Коэффициенты
- •Александр Васильевич Велыможин Владислав Александрович Гудков Леонид Борисович Миротин
- •400131, Волгоград, ул. Советская. 35
- •400131, Волгоград, ул. Коммунистическая. 21, тел.34-99-69
- •404126. Волжский, ул. Пушкина, 79
Итерация 1
Базисные переменные |
Рассматриваемое пробное решение |
Коэффициент при Х4 |
Значения отношений |
Минимальное значение |
Следующее пробное решение |
Х0 |
0 |
- 11 |
- |
- |
- |
Х5 |
15 |
1 |
15 |
- |
- |
Х6 |
120 |
2 |
60 |
- |
- |
Х7 |
100 |
15 |
100/15 |
6,67 |
Х4 = 6,67; Х7=0 |
Шаг 4. Перепишем соотношения (7.55) таким образом, чтобы в строке 3 коэффициент при Х4 был равен единице, а в строках 0, 1 и 2 -нулю. Процедуру, с помощью которой это достигается, называют операцией замены базиса. Сначала разделим обе части уравнения в строке 3 на коэффициент при Х4, т. е. на 15

![]()
(7.56)
Обратим в нули коэффициенты при Х4 в строках 0,1,2, действуя по следующей схеме:
умножить строку 3 на 11 и результат прибавить к строке 0;
умножить строку 3 на — 1 и результат прибавить к строке 1;
умножить строку 3 на — 2 и результат прибавить к строке 2.
В результате получим
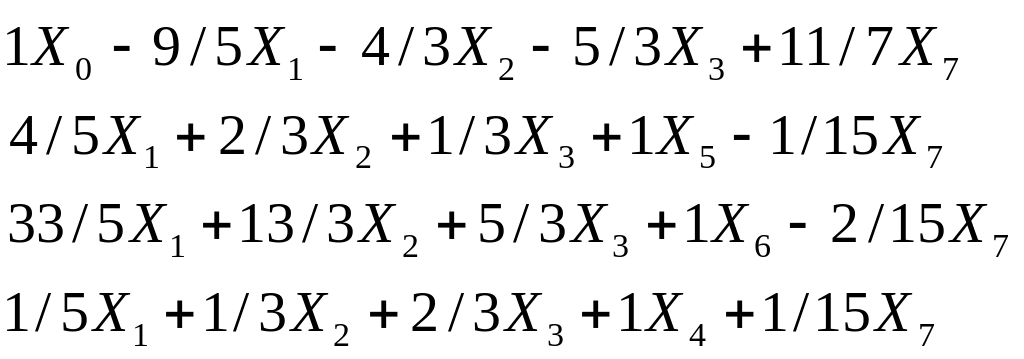
![]()
Полученное уравнение (7.57) эквивалентно уравнению (7.55). Его удобство заключается в том, что, полагая Х1 = Х2= ... = Х6 = Х7 = 0, сразу можно определить значения переменных для нового пробного базисного решения. Х0 = 220/3, Х5 = 25/3, Х6 = 320/3, Х4 = 20/3. Прибыль для нового пробного решения равняется прибыли при предыдущем пробном базисе плюс значение новой базисной перемен-
ной, умноженной на удельный вклад новой базисной переменной, в приращении прибыли:
220 / 3 = 0 + 20/3*11 .
Смысл правила 2 становится теперь более ясным. Если бы вместо Х7 из первоначального базиса исключить X5 (или Х6), то Х4, Х7, Х6 (или X5) приняли бы отрицательное значение, что противоречит предположению о том, что ни одна из переменных не может быть отрицательной.
Итерация 2. Завершив первую итерацию, следует вернуться к шагу 2, с тем чтобы определить, является ли полученное решение оптимальным. Если оптимум еще не достигнут, необходимо в соответствии с симплексным алгоритмом приступить к следующей итерации. Согласно правилу 1, возможность улучшить решение существует.
Таблица 37
Итерация 2
Базисные переменные |
Рассматриваемое пробное решение |
Коэффициент при Х1 |
Значения отношений |
Минимальное значение |
Следующее пробное решение |
Х0 |
220/3 |
- 9/5 |
- |
- |
- |
Х5 |
25/3 |
4/5 |
125/12 |
125/12 |
Х1 = 125/12; Х5=0 |
Х6 |
320/3 |
33/5 |
1600/99 |
- |
- |
Х4 |
20/3 |
1/5 |
100/3 |
- |
- |
При этом в очередной базис можно включить либо Х1 либо Х2 либо Х3. На основании правила 1 выбор падает на Х1 так как эта переменная обеспечивает наибольшее удельное приращение для значения целевой функции.
(7.57)

![]()
(7.58)
Затем исключим X, из уравнений в строках 0, 2, 3, действуя по следующей схеме:
262
263
умножить строку 1 на 9/5 и результаты сложить со строкой 0;
умножить строку 1 на - 33/5 и результаты сложить со строкой 2;
умножить строку I на - 1/5 и результаты сложить со строкой 3.
В
![]() результате получим:
результате получим:
Третье пробное базисное решение дало следующие результаты:
Х0= 1105/12, Х1= 125/12, Х6= 455/12, Х4= 55/12.
Итерация 3. Завершив вторую симплекс-итерацию, видим (строка 0), что решение может быть улучшено за счет X3. Определим, какая переменная должна быть исключена из базиса.
Пронормируем коэффициент X3 в строке 3 путем деления обеих частей соответствующего уравнения на 7/12 и исключим X3 из уравнений в строках 0,1 и 2 следующим образом:
умножить строку 3 на 11/12 и результат сложить со строкой 0;
умножить строку 3 на - 5/12 и результат сложить со строкой 1;
умножить строку 3 на 13/12 и результат сложить со строкой 2.
В результате получим:
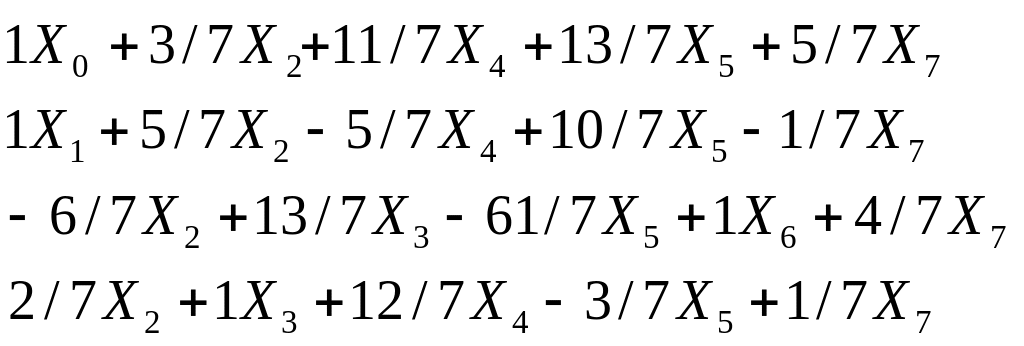
![]()
В строке 0 все коэффициенты положительны, следовательно, согласно правилу 1, полученное решение является оптимальным (табл. 38).
Таблица 38
Итерация 3
(7.59)
Базисные переменные |
Рассматриваемое пробное решение |
Коэффициент при Х3 |
Значения отношений |
Минимальное значение |
Следующее пробное решение |
Х0 |
1105/12 |
- 11/12 |
- |
- |
- |
Х1 |
125/12 |
5/12 |
25 |
- |
- |
Х6 |
455/12 |
-13/12 |
- |
- |
Х3 = 55/7,
|
Х4 |
55/12 |
7/12 |
55/7 |
55/7 |
Х4=0 |
Коэффициенты при переменных в окончательном варианте строки 0 иногда называют скрытыми издержками. Каждый коэффициент определяет отклонение значения целевой функции от оптимального при увеличении значения соответствующей небазисной переменной на единицу. Таким образом, предприятие будет иметь прибыль 695/7 при выпуске продукции по технологическому процессу 1 и 3.
В кратком изложении симплексный метод состоит в следующем:
Шаг 1 . Выбирается исходный базис.
Шаг 2. Используется правило 1. Если рассматриваемое пробное решение не является оптимальным, осуществляется переход к шагу 3. В противном случае вычисления прекращаются.
Шаг 3. Выполняется процедура, предписанная правилом 2.
Шаг 4. Сменяется базис, после чего возвращаются к шагу 2.
