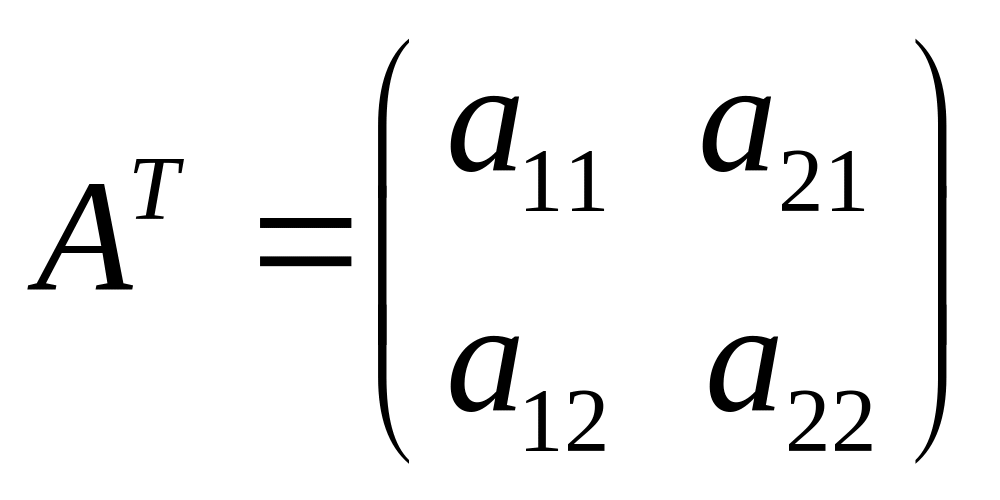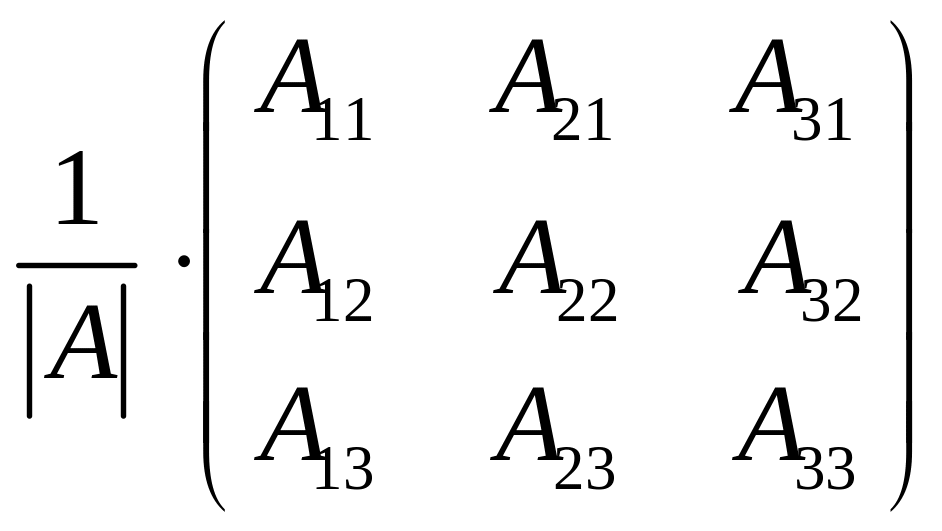- •І. Загальні положення
- •Уміння, на формування яких націлене навчання:
- •Стисла робоча програма (осінній семестр)
- •Тематика лекцій
- •2.2 Тематика практичних занять
- •Разом: 64 годин
- •Питання для самоперевірки
- •Навчальна література
- •Опорний конспект лекції „Визначники”
- •Характеристики визначників:
- •Властивості визначників:
- •Обчислення визначників
- •Конспект – схема лекції „Матриці”
- •Матриці
- •Характеристики матриць:
- •Властивості матриць:
- •Алгоритми знаходження оберненої матриці:
- •Ранг матриці
- •Методи визначення рангу матриць
- •Властивості рангу матриць:
- •Лінійна залежність
- •Конспект – схема лекції
- •Лінійні рівняння
- •Системи лінійних рівнянь
- •Види систем:
- •Елементарні перетворення системи
- •Критерій сумісності системи рівнянь
- •Методи розв’язання систем
- •Конспект – схема лекцій з
- •Вектори
- •Основні поняття
- •Характеристики змінних величин
- •Множини.
- •Дії над множинами
- •Область визначення (існування) функції – одз
- •Характеристики функцій:
- •Теорія границь
- •Означення границі
- •Властивості границь
- •Основні теореми про границі функцій
- •Нескінченно малі та нескінченно великі
- •Властивості еквівалентних функцій
- •Обчислення границь
- •Неперервність функцій
- •Точки розриву функції
- •Класифікація точок розриву
- •Правила відшукання точок розриву:
- •Модуль №1. Елементи лінійної алгебри
- •3.1.2. Практичні заняття
- •Методи цілеспрямованого формування у студентів уміння
- •Аналіз конкретних ситуацій.
- •Метод еврестичного дослідження (когнітивний).
- •11. Проблемний метод.
- •3.2. Види організації самостійної роботи, що виконуються студентами у позаурочний час.
- •Самостійні домашні роботи
- •Корекція самостійної роботи
- •Атестаційне тестування
- •Тест № 1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 7
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •1.Визначте вид матриці (прямокутна , квадратна другого порядку, діагональна третього порядку, одинична третього порядку, нульова , матриця-стовпець, матриця-рядок):
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест № 1
- •Тест № 6
- •Тест № 7
- •5. Знайти геометричне місце точок, рівновіддалених від точок :
- •Тест № 8
- •Тест № 9
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест №1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 15
- •Тест № 16
- •Тест № 17
- •Тест № 19
- •Тест № 20
- •Тест № 21
- •Тест № 22
- •2. Встановити, якою є функція (неперервною чи розривною)
- •Тест № 23
- •Тест № 24
- •Тест № 26
- •Тест № 27
- •Тест № 28
- •Тест № 29
- •Завдання 2.
- •Завдання 3.
- •2) По правилу трикутника:
- •3) По правилу Саруса:
- •4) Штучного доповнення:
- •Завдання 6.
- •Завдання 7.
- •Завдання 8.
- •Завдання 9.
- •Завдання 10.
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Додаток 3. Допуск (перевірка готовності) до лекцій:
- •Тема „Матриці”
- •Тема „Системи лінійних алгебраічних рівнянь”
Обчислення визначників
Порядок |
Закон |
Формула |
І |
Число |
|
ІІ |
2 рядка та 2 стовпця
|
|
ІІІ
3 рядка
та 3 с |
елементами будь-якого рядка або стовпця - Правило Лапласа: Визначник дорівнює сумі додатків єлементів рядка (стовпця) на відповідні алгебраічні доповнення
трикутника
∆ =
Визначник доповнюється двома першими рядками або стовпцями і записується сумма добутків елементів, що стоять на діагоналях |
∆ =
= a1(-1)1+1
+
b1(-1)1+2
+
c1(-1)1+3
∆ =
=
=
= _ =
=
|
n |
Визначники вищих порядків Розкриття здійснюється двома шляхами: 1. За елементами будь-якого рядка або стовбця із зниженням порядку визначника. 2. Створенням як можна більшої кількості нулів в будь-якому рядку або стовбці.
|
Визначник n-го порядку дорівнює сумі добутків елементів:
1)
будь-якого
стовбця
на відповідні
алгебраічні
доповнення:
2)
будь-якого
рядка на
відповідні
алгебраічні
доповнення:
|
Конспект – схема лекції „Матриці”
1. Означення визначників.
2. Характеристики визначників.
3. Властивості визначників.
4. Обчислення визначників.
Матриці
Це впорядковані таблиці числових або літерних значень з m рядків та n стовпців
А |
Характеристики матриць:
10. Матриці еквівалентні, якщо одна з них отримана з іншої шляхом елементарних перетворень. А ~ В.
|
Види матриць:
№ |
Назва та означення |
Формула |
1 |
Матриця - рядок |
|
2 |
Матриця - стовпець |
|
3 |
Квадратна матриця – якщо кількість рядків і стовпців однакові: |
|
4 |
Прямокутна матриця – якщо
кількість рядків і стовпців різні:
|
|
5 |
Нульова матриця – якщо всі елементи дорівнюють нулю. |
|
6 |
Особлива (вироджена) -квадратна матриця, виз-начник якої дорівнює 0. |
|
7 |
Невироджена -квадратна матриця, визначник якої відмінний від нуля. |
|
8 |
Ступінчата - квадратна матриця, якщо в окремих рядках один елемент відмінний від 0, а всі інші дорівнюють нулю. |
|
9 |
Діагональна - ступінчата матриця, якщо відмінні від 0 елементи стоять на головній діагоналі. |
|
10 |
Скалярна - діагональна матриця, елементи якої рівні між собою. |
|
11 |
Одинична – скалярна матриця, елементи якої на головній діагоналі 1.
|
|
Дії над матрицями
Матрицю неможливо обчислити! |
При будь-яких діях над матрицями завжди отримують матрицю.
|
Матриці рівні тоді і тільки тоді, коли вони мають однаковий розмір та однакові відповідні елементи:
А =
В
|
№ |
Дія, закон |
Формула |
1 |
Додавання матриць. Сума двох матриць А і В – інша матриця, кожен елемент якої дорівнює сумі відповідних елементів матриць А і В. |
А
+ В = С, тобто
|
2 |
Віднімання матриць. Різниця двох матриць А і В – інша матриця, кожен елемент якої дорівнює різниці відповідних елементів матриць А і В. |
-
=
А
- В = Д, тобто
|
3 |
Множення матриць на число. Добутком матриці А на число k – інша матриця, кожен елемент якої дорівнює добутку відповідних елементів матриці А на число k. |
kА =
k
=
kА
= С, тобто
|
4 |
Множення матриць. Добуток двох матриць А і В – інша матриця, кожен елемент якої дорівнює сумі добутків елементів i-го рядка матриці А на відповідні елементи j-го стовпця матриці В. |
А∙В
=
∙
=
=
А∙В
= С, де
|
5 |
Піднесення матриці А до степеня n (можливе лише для квадратних матриць) – множення матриці саму на себе n разів. |
|
6 |
Транспонування матриць
|
А
=
,
|
7 |
Обертання – процес знаходження оберненої матриці |
А-1
=
|
8 |
Ділення матриць |
|

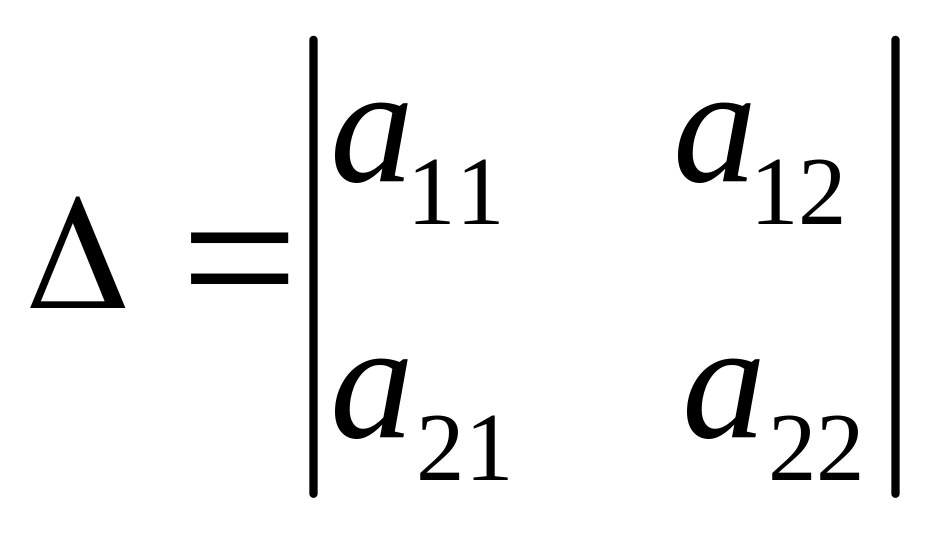 = а
= а товпця
товпця
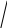
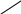
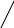

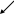
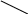
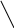 «+»
«+»






 =
=
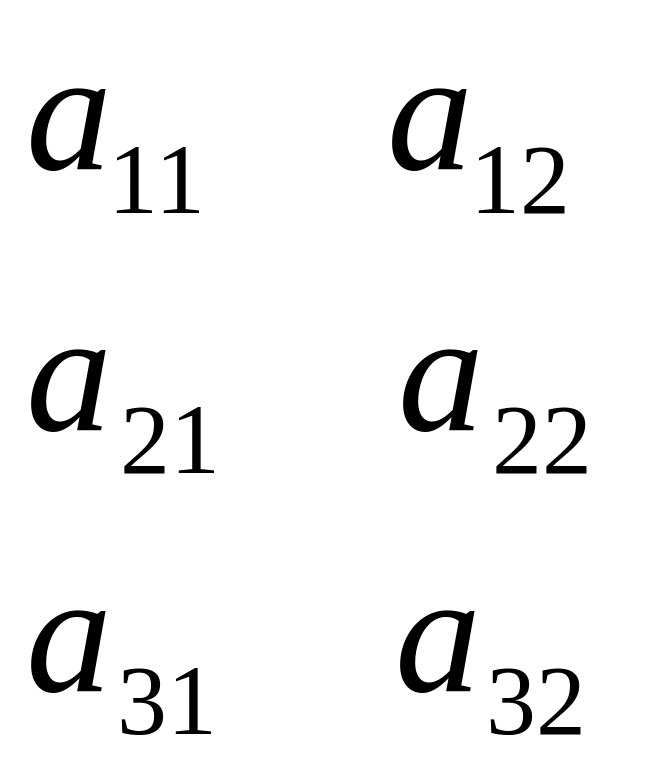 =
=
=
=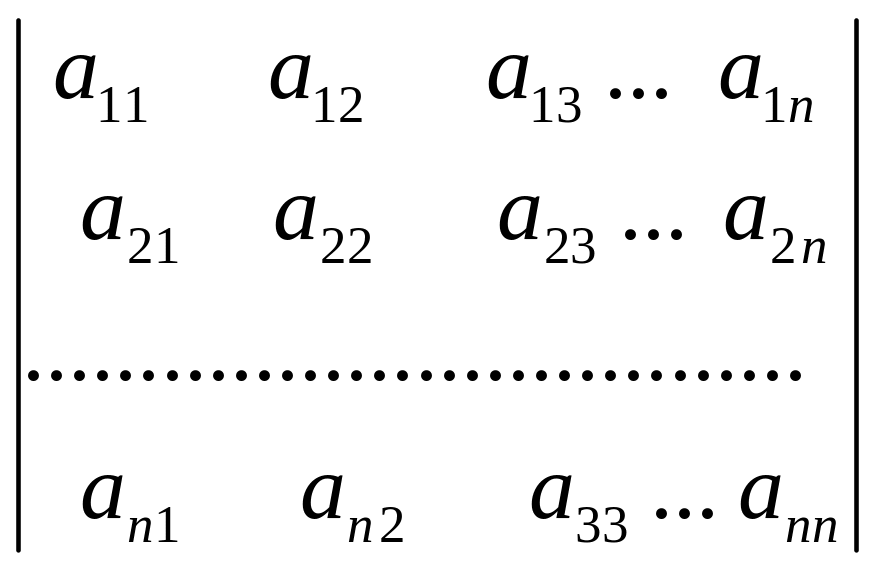
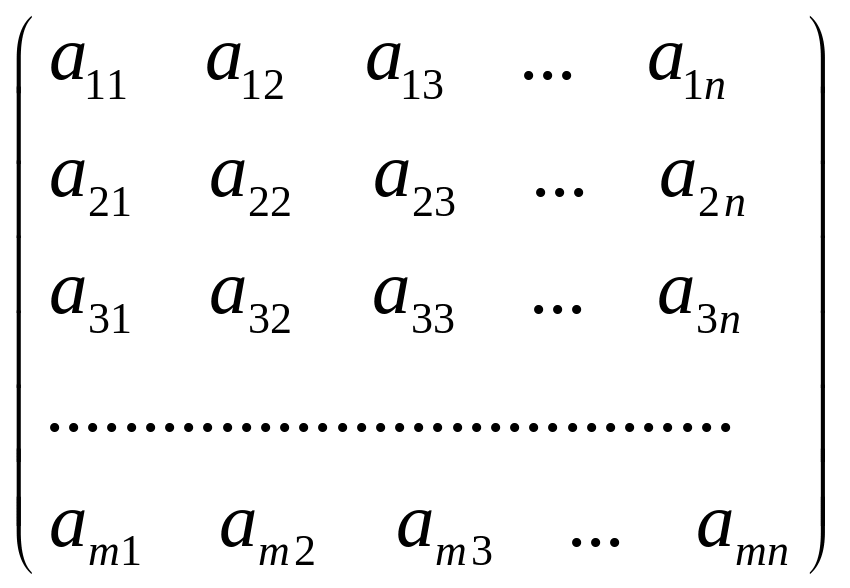
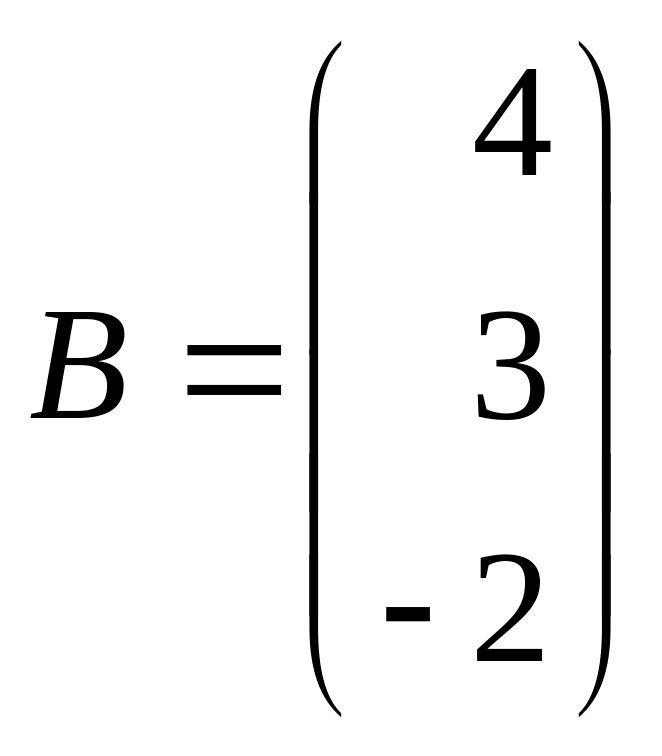 ,
,
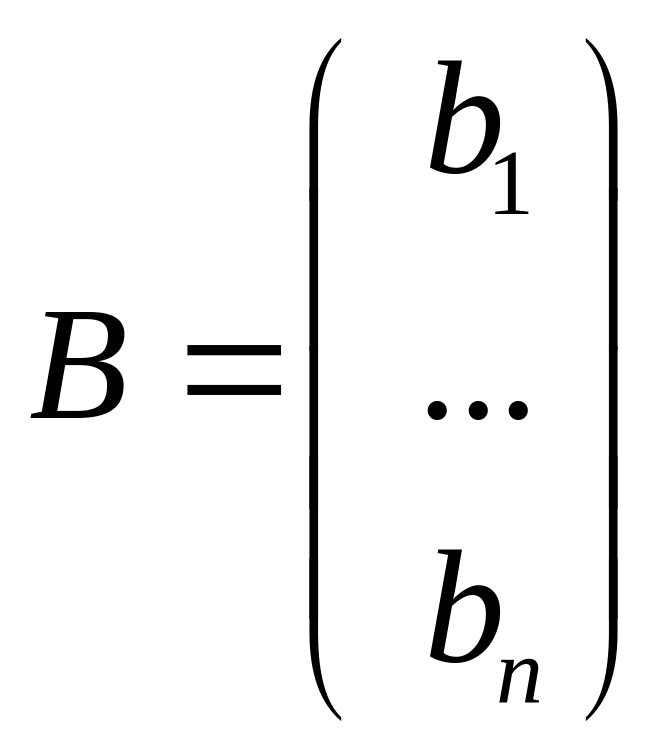
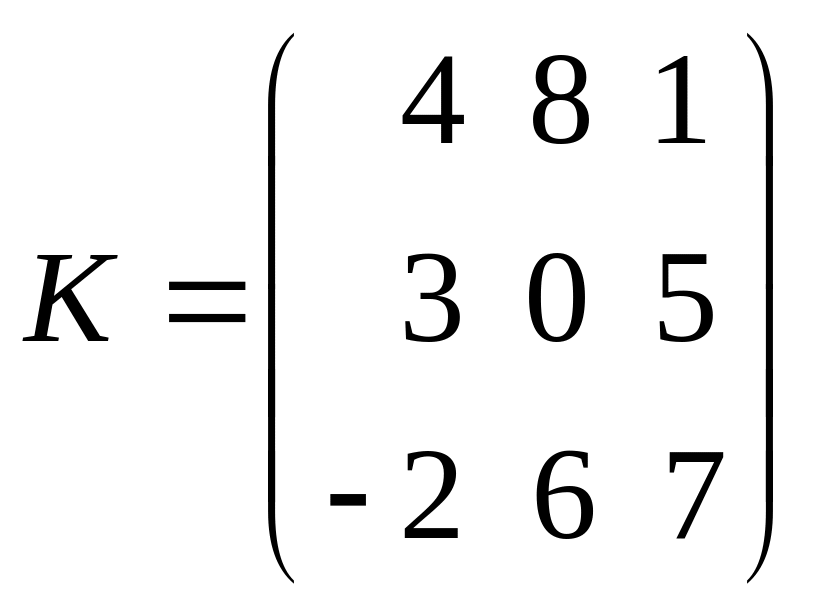 ,
,
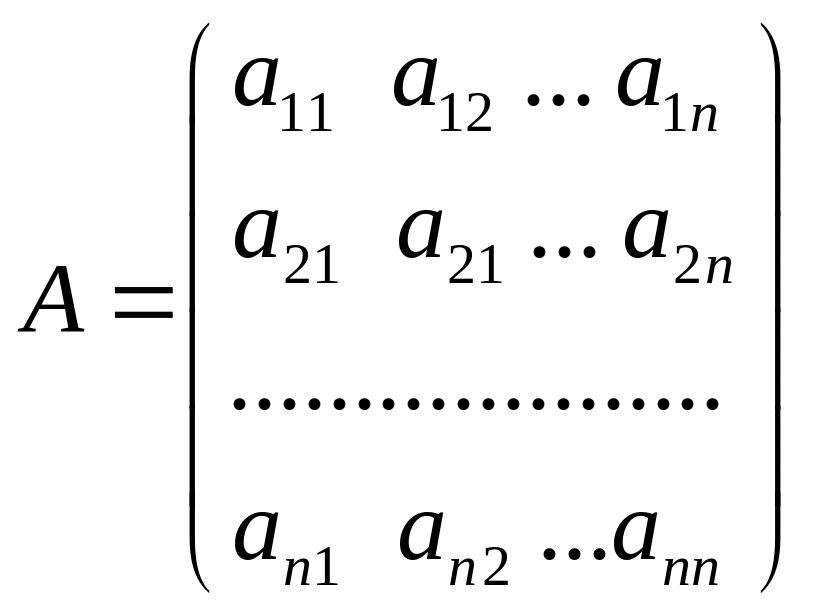
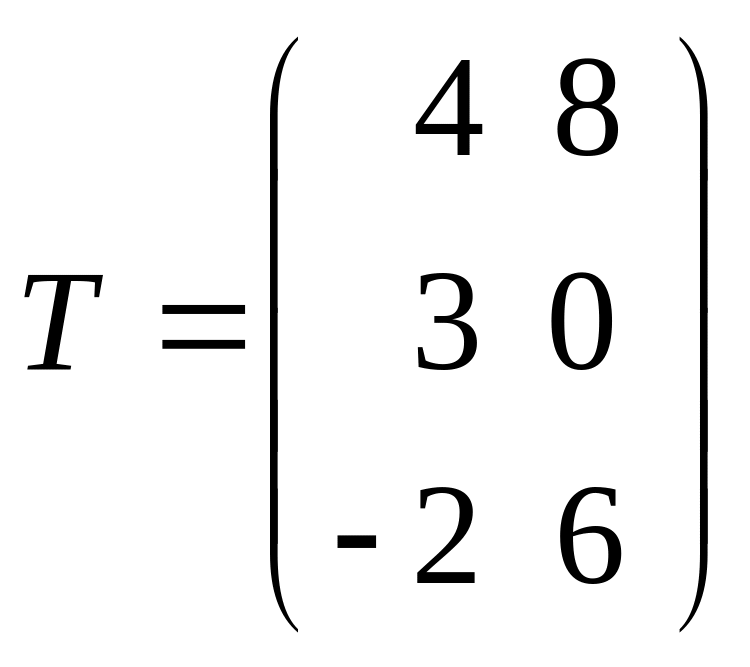 ,
,
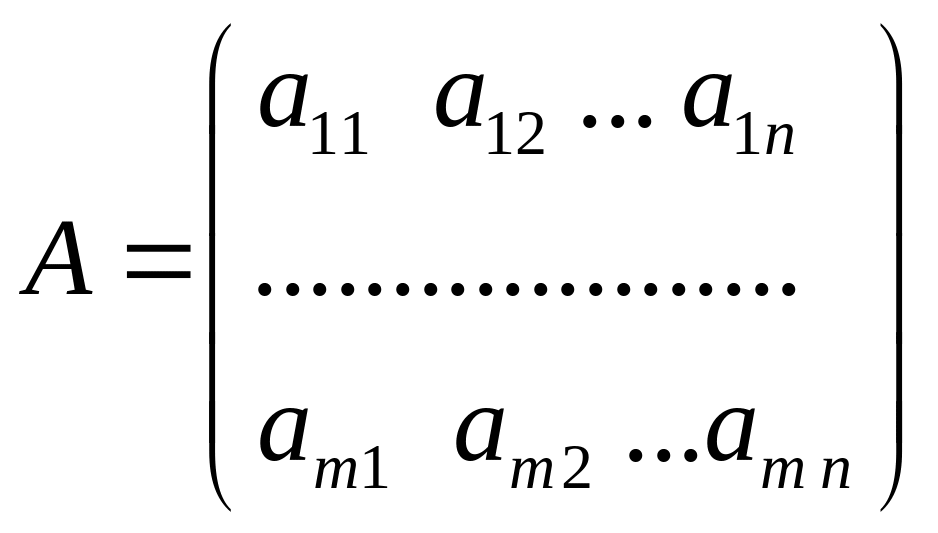
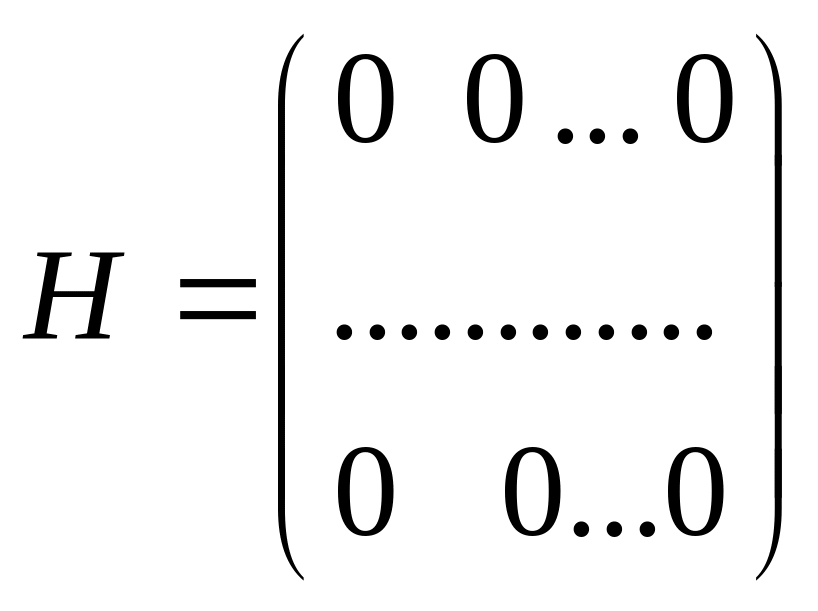
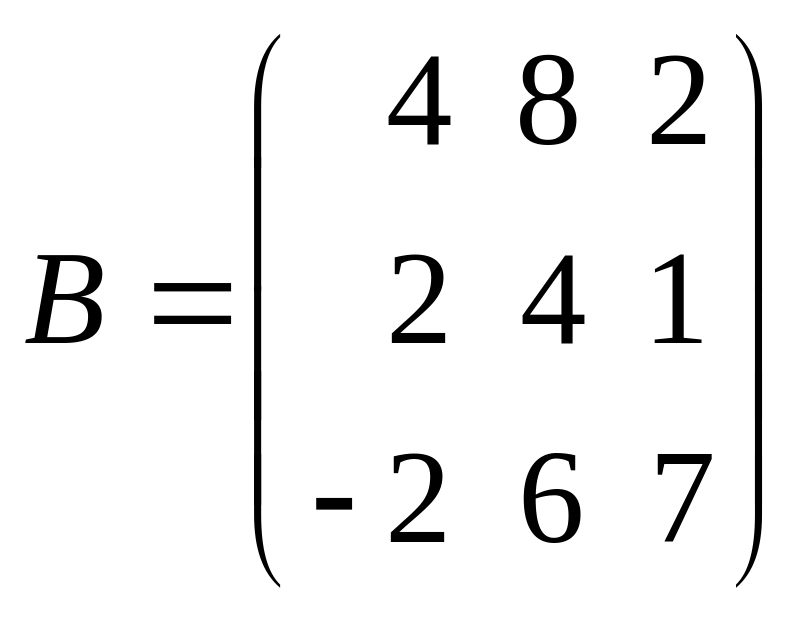
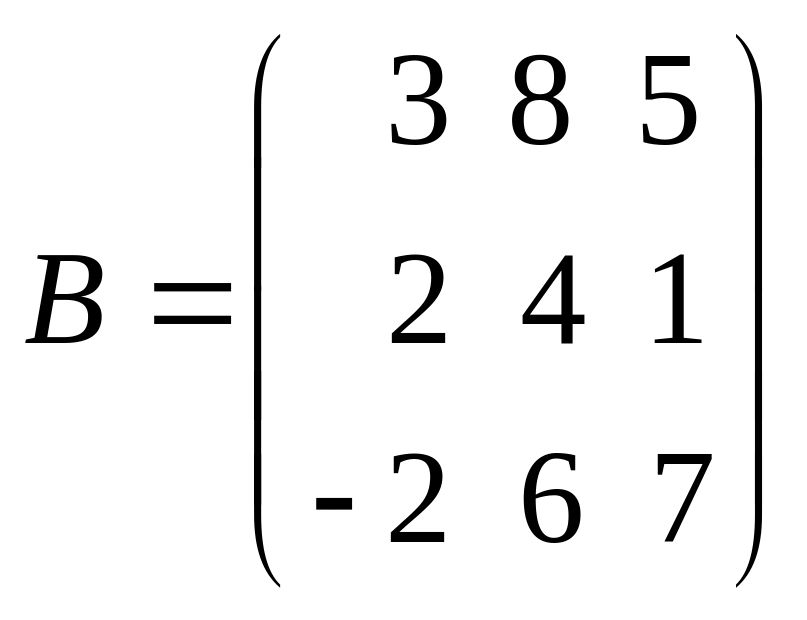
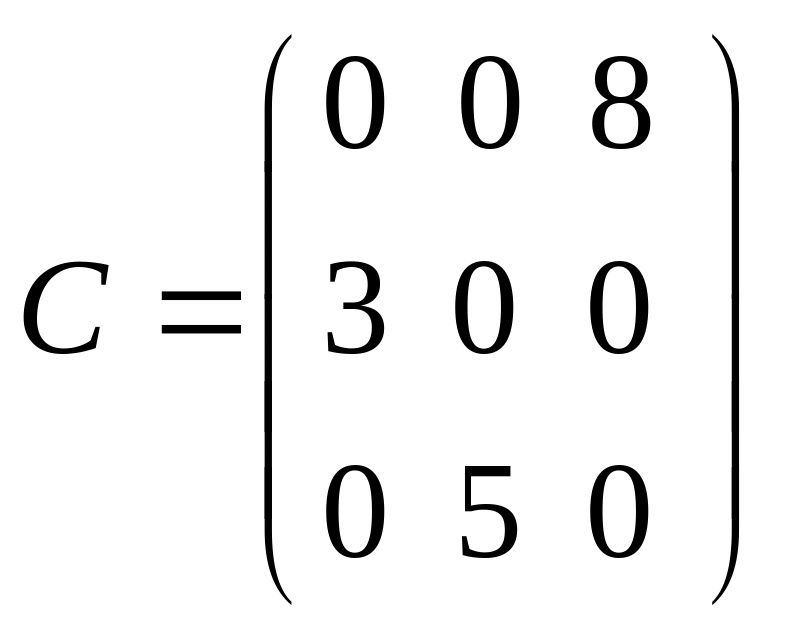 ,
,
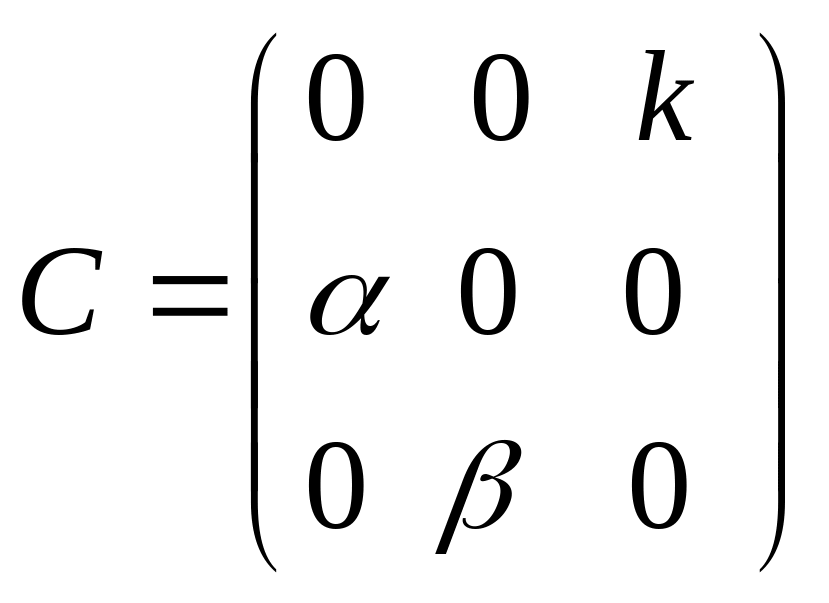
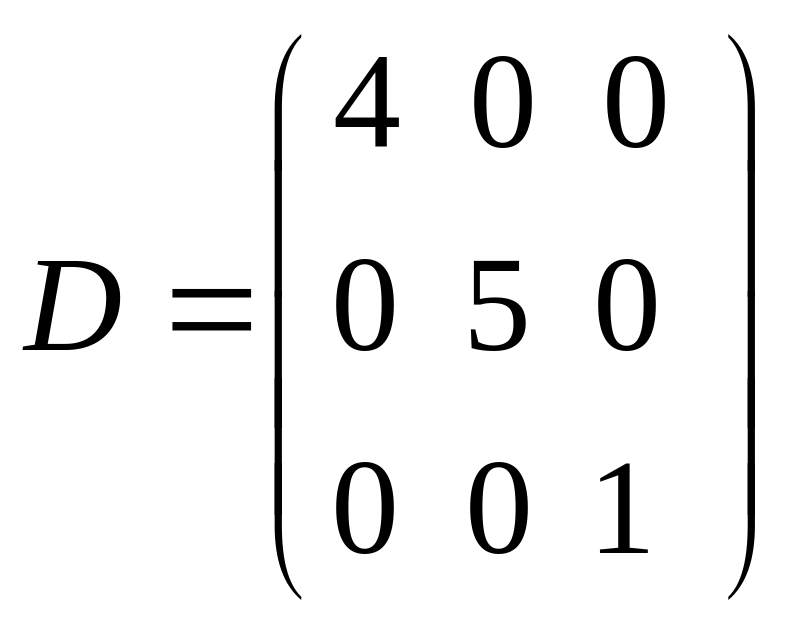 ,
,
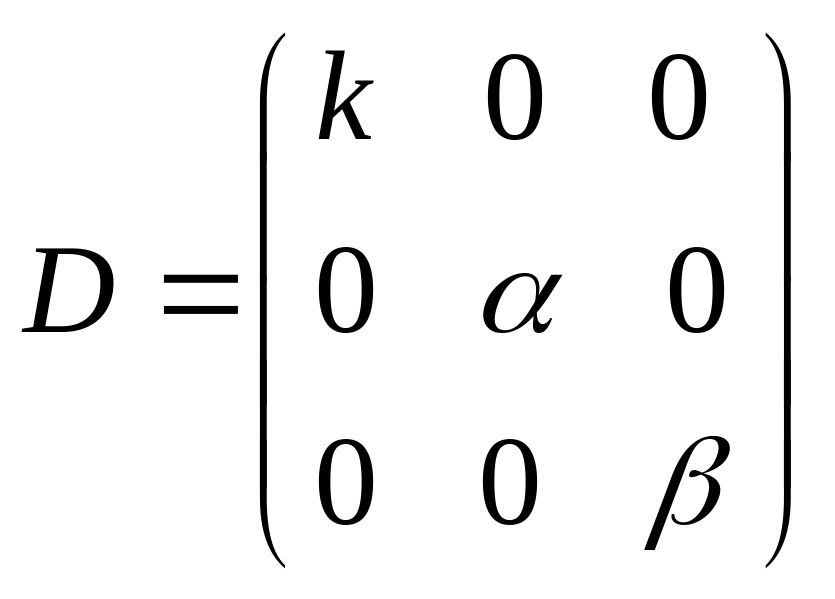
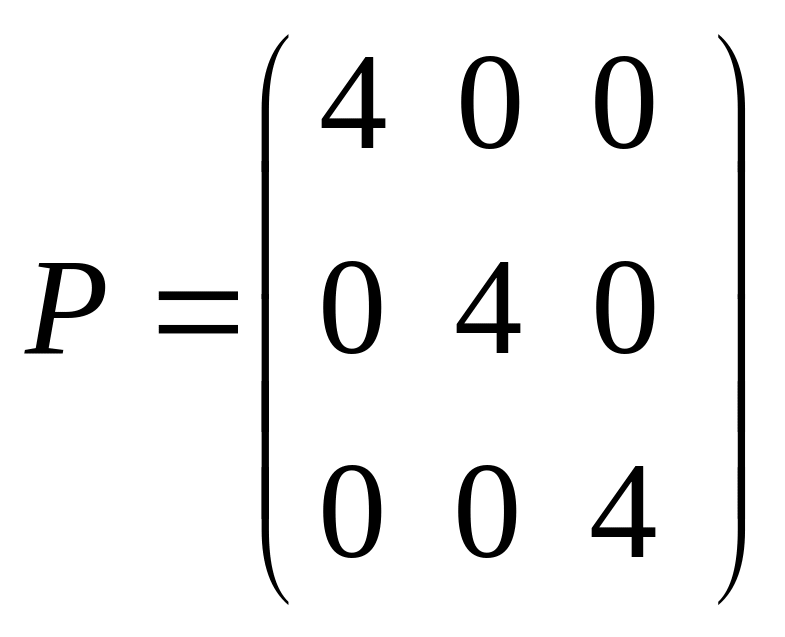 ,
,
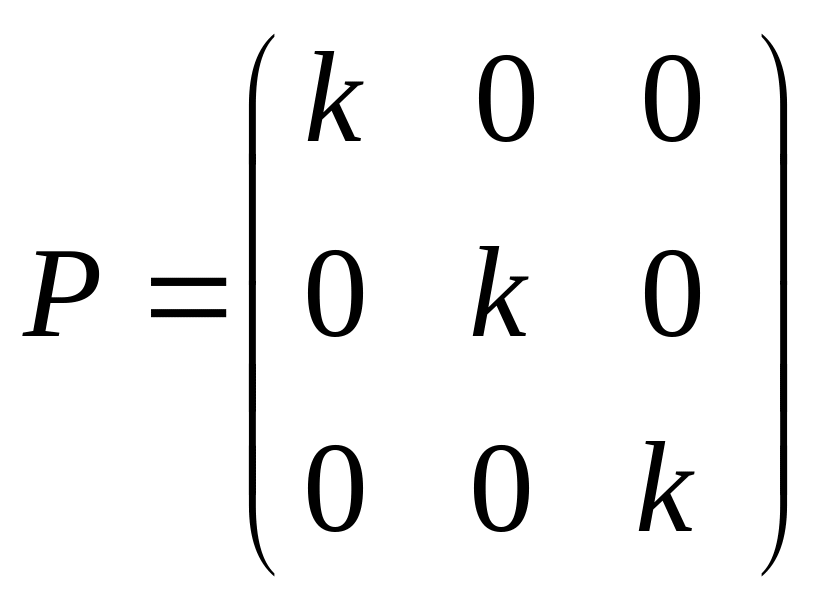
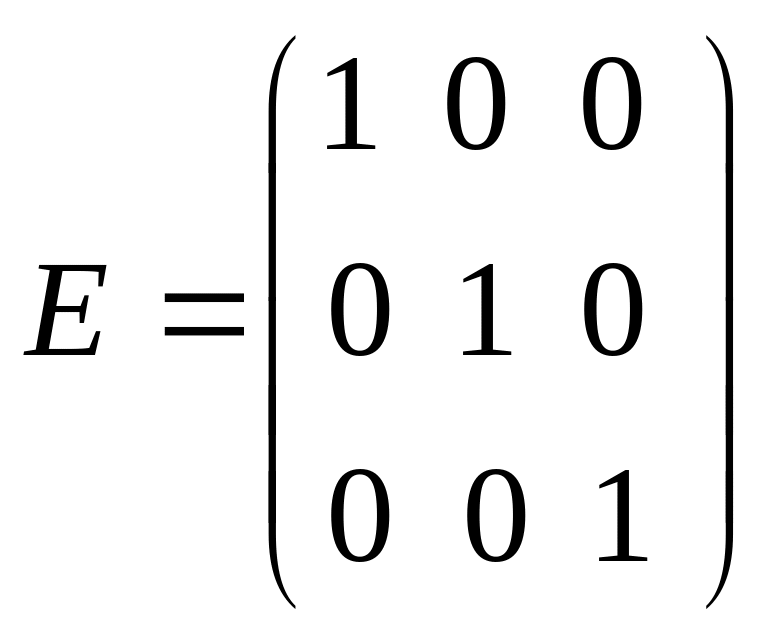 .
.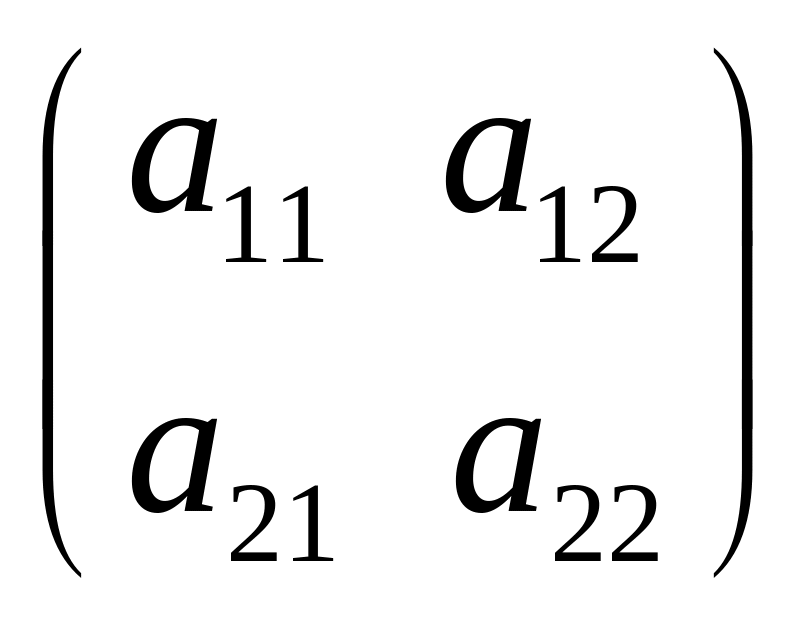 +
+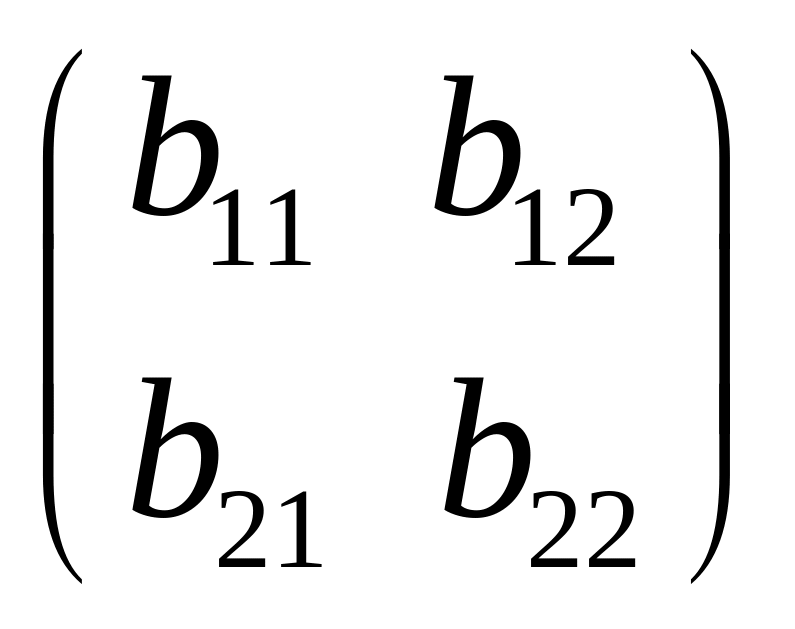 =
=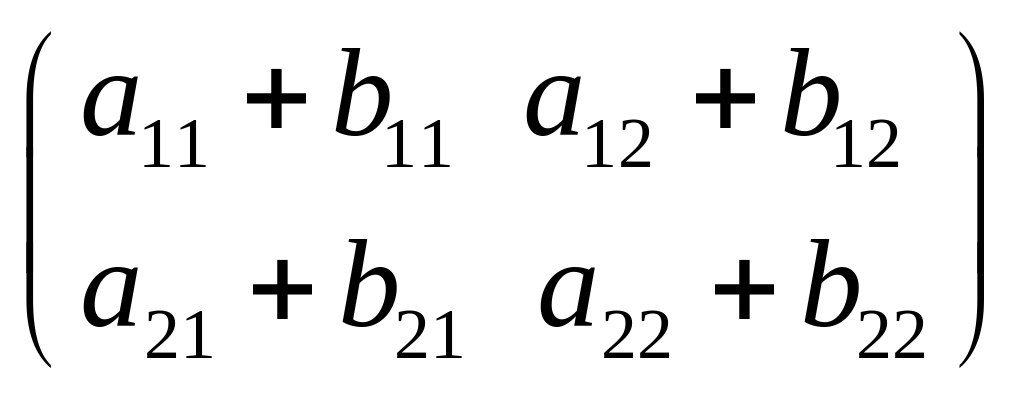
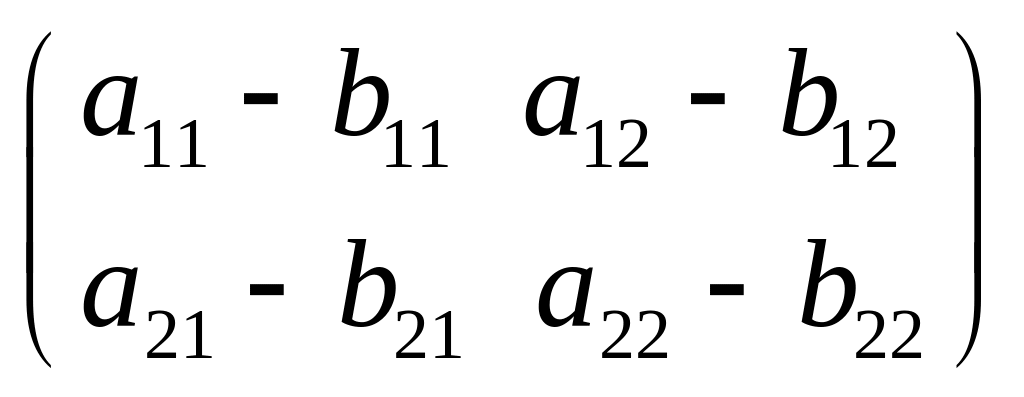

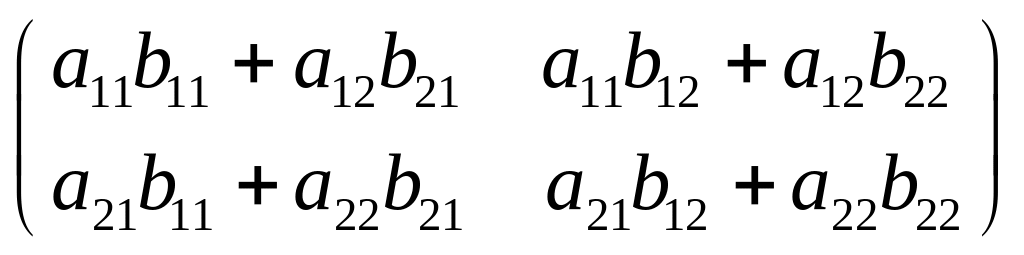 ,
,