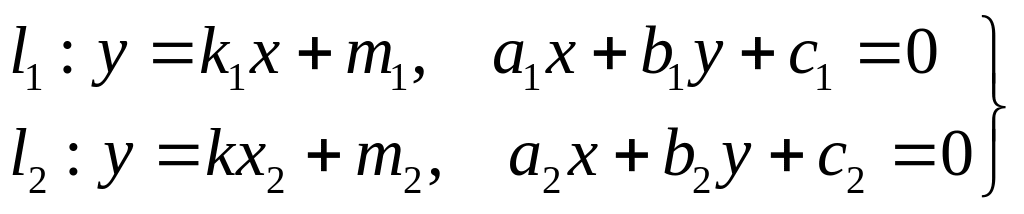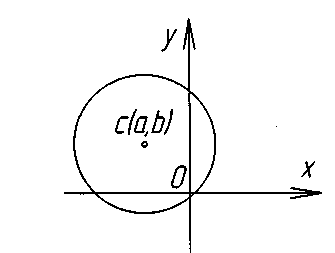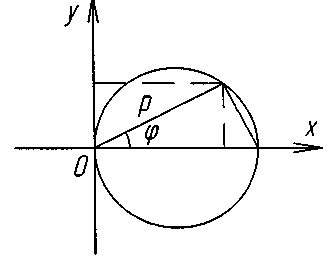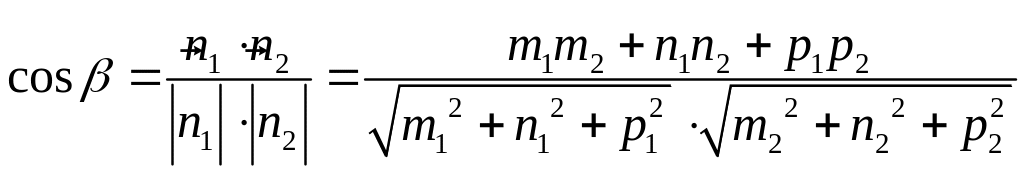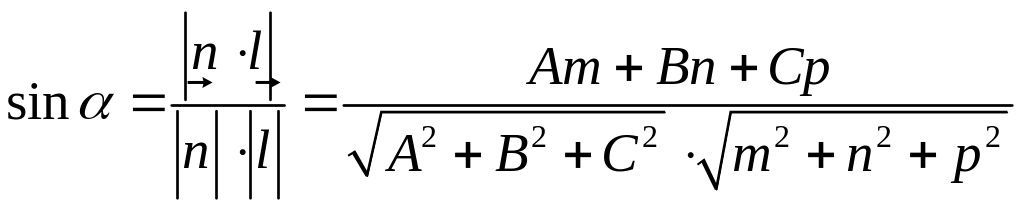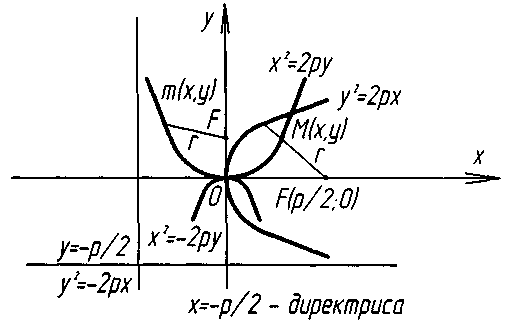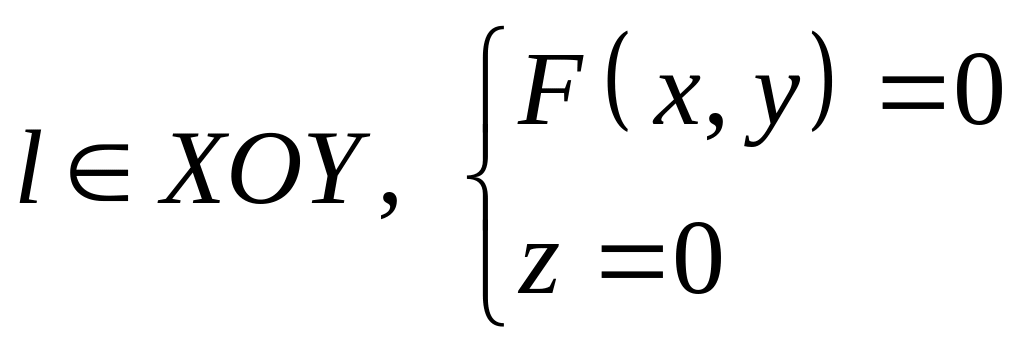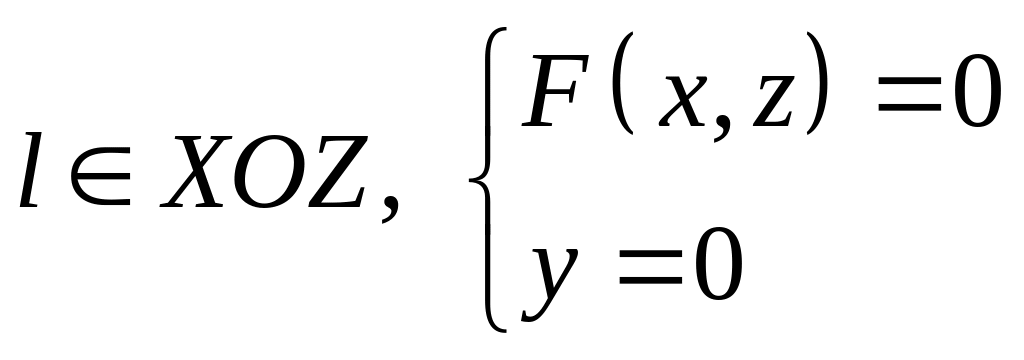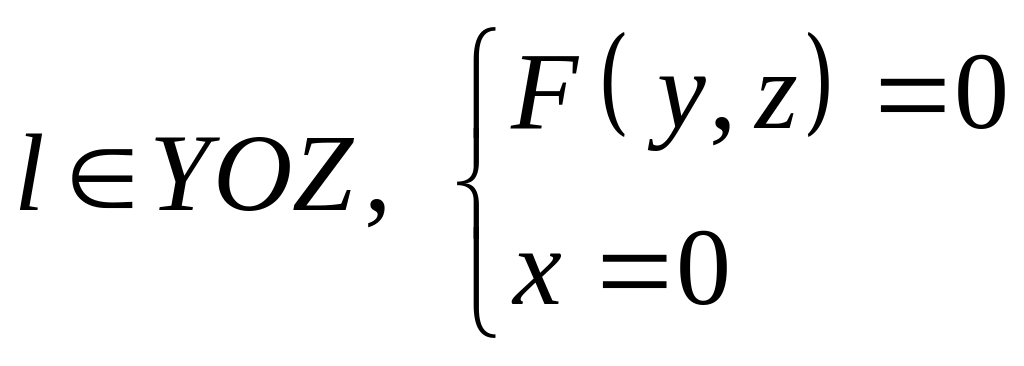- •І. Загальні положення
- •Уміння, на формування яких націлене навчання:
- •Стисла робоча програма (осінній семестр)
- •Тематика лекцій
- •2.2 Тематика практичних занять
- •Разом: 64 годин
- •Питання для самоперевірки
- •Навчальна література
- •Опорний конспект лекції „Визначники”
- •Характеристики визначників:
- •Властивості визначників:
- •Обчислення визначників
- •Конспект – схема лекції „Матриці”
- •Матриці
- •Характеристики матриць:
- •Властивості матриць:
- •Алгоритми знаходження оберненої матриці:
- •Ранг матриці
- •Методи визначення рангу матриць
- •Властивості рангу матриць:
- •Лінійна залежність
- •Конспект – схема лекції
- •Лінійні рівняння
- •Системи лінійних рівнянь
- •Види систем:
- •Елементарні перетворення системи
- •Критерій сумісності системи рівнянь
- •Методи розв’язання систем
- •Конспект – схема лекцій з
- •Вектори
- •Основні поняття
- •Характеристики змінних величин
- •Множини.
- •Дії над множинами
- •Область визначення (існування) функції – одз
- •Характеристики функцій:
- •Теорія границь
- •Означення границі
- •Властивості границь
- •Основні теореми про границі функцій
- •Нескінченно малі та нескінченно великі
- •Властивості еквівалентних функцій
- •Обчислення границь
- •Неперервність функцій
- •Точки розриву функції
- •Класифікація точок розриву
- •Правила відшукання точок розриву:
- •Модуль №1. Елементи лінійної алгебри
- •3.1.2. Практичні заняття
- •Методи цілеспрямованого формування у студентів уміння
- •Аналіз конкретних ситуацій.
- •Метод еврестичного дослідження (когнітивний).
- •11. Проблемний метод.
- •3.2. Види організації самостійної роботи, що виконуються студентами у позаурочний час.
- •Самостійні домашні роботи
- •Корекція самостійної роботи
- •Атестаційне тестування
- •Тест № 1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 7
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •1.Визначте вид матриці (прямокутна , квадратна другого порядку, діагональна третього порядку, одинична третього порядку, нульова , матриця-стовпець, матриця-рядок):
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест № 1
- •Тест № 6
- •Тест № 7
- •5. Знайти геометричне місце точок, рівновіддалених від точок :
- •Тест № 8
- •Тест № 9
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест №1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 15
- •Тест № 16
- •Тест № 17
- •Тест № 19
- •Тест № 20
- •Тест № 21
- •Тест № 22
- •2. Встановити, якою є функція (неперервною чи розривною)
- •Тест № 23
- •Тест № 24
- •Тест № 26
- •Тест № 27
- •Тест № 28
- •Тест № 29
- •Завдання 2.
- •Завдання 3.
- •2) По правилу трикутника:
- •3) По правилу Саруса:
- •4) Штучного доповнення:
- •Завдання 6.
- •Завдання 7.
- •Завдання 8.
- •Завдання 9.
- •Завдання 10.
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Додаток 3. Допуск (перевірка готовності) до лекцій:
- •Тема „Матриці”
- •Тема „Системи лінійних алгебраічних рівнянь”
Конспект – схема лекцій з
„Аналітичної геометрії”
1. Вектори.
2. Пряма на площині.
3. Пряма у просторі.
4. Криві 2 порядку.
6. Полярна система координат.
5. Площина у просторі.
6. Поверхні 2 порядку.
Аналітична геометрія
Це розділ математики, в якому геометричні об’єкти вивчають засобами алгебри на основі метода координат. Виникла в 17 ст. Декарт. Предметом аналітичної геометрії є вивчення геометричніх образів алгебраічними методами. Засоби досліджень: метод координат і алгебра. Кожна точка на площині ототожнюється з упорядкованою парою, а в просторі – з трійкою чисел – координатами цієї точки.
Найпростіші задачі аналітичної геометрії:
М1
і М2
.
Точка М(х; у; z) поділяє відрізок М1
М2
в данному відношені:
Якщо
точка М поділяє відрізок навпіл:
Основні задачі аналітичної геометрії:
Основні поняття: Найпростіші геометричні образи: точки, прямі, площини, криві, поверхні 2 порядку. Вісь – пряма лінія з вказани на ній напрямком. Напрямлений – відрізок на вісі, якщо вказано яка з його граничних точок є початком і є кінцем. Нульовий відрізок – напрямлений відрізок, коли точки початку і кінця співпадають. Величина напрямленого відрізку – число, що дорівнює довжині відрізка (із знаком „+”, коли напрямок відрізка співпадає з напрямком вісі та із знаком „-„ в протилежному. 2 ненульові напрямлені відрізка рівні, якщо при суміщенні їх початків співпадають їх кінці. |
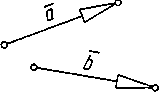
Вектори
Розрізняють скалярні величини та векторні. Скалярна – величина, яка характеризується числовим значенням (модулем). Вектор
- величина,
яка характеризується не лише числовим
значенням, а й напрямком.
Нульовий – вектор, у якого початок і кінець співпадають, довжина дорівнює нулю. Він не має напрямку – напрям довільний.
Колінеарні
- вектори, які лежать на одній прямій
або на паралельних прямих. Кут між
ними дорівнює 0, відповідні координати
пропорційні
Вектори рівні, якщо вони сполучаються паралельним переносом (рівні за величиною та співпадають за напрямком). У них рівні координати, довжини та напрями. Це колінеарні вектори. Одиничний – вектор, довжина якого дорівнює одиниці. Протилежні – паралельні вектори з однаковою довжиною і протилежного напрямку. Компланарні - вектори, які лежать в одній площині або на паралельних площинах. Вільні – вектори, початкова точка яких оберається довільно. Приєднані (зв’язані) – вектори, для яких важлива точка приложення. |
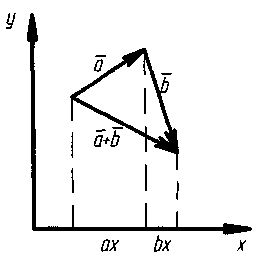
О – початок, М – кінець
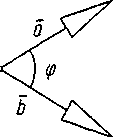
Кут між векторами - кут між рівними їм векторами з загальним початком.
Координати
Властивості суми:
1.
2.
3.
4.
|
Колінеарні
вектори:
Операции над векторами.
На площині:
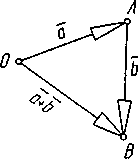
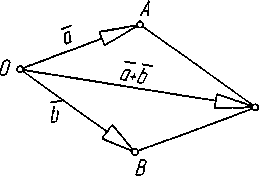
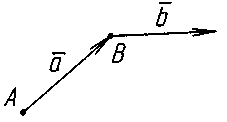
Додавання:
1. Правило треугольников.
2. Правило параллелограмма.
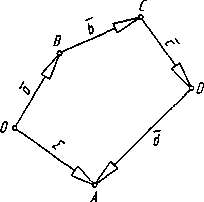
3. Правило многокутника.
У просторі:
М |
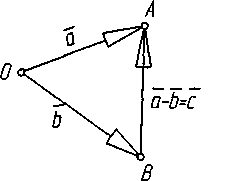
Різниця
Вектор
а) збільшений у λ раз, якщо λ>1 б) в λ раз зменшений, якщо 0< λ< 1 в) протилежно спрямований, якщо λ < 0. |
Різниця
–
це
третій вектор,
проведений
із
кінця
віднімаємого
до
кінця
зменшуваного,
який
при
складанні
з
вектором
Множення
вектора на число –
це новий
вектор
,
довжина
якого
Властивості:
1
2)
3)
4)
5)
6)
|
Вектори
Якщо
вектор утворює з віссю ОХ кут φ, то
проекція вектора на вісь – це добуток
модуля вектора на
Властивості:
1. Рівні вектори мають рівні проекції на одну вісь:
2.
Проекція суми векторів дорівнює сумі
проекцій векторів на цю вісь:
3.
4.
5. Проекція замкненої векторної лінії на вісь є нуль. (2 і 3 – лінійні властивості проекції).
На площині
Механічний сенс:
А = Fcosφ
Механічний сенс – це момент вектора відносно точки А.
|
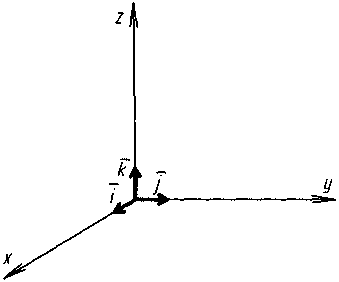
Орти
-
одинічні вектори, спрямовані вздовж
вісі координат
.
Їх
координати
d
можна
розкласти
по 3 некомпланарним
векторам:
К
Проекція вектора на вісь – це довжина напрямленого відрізку прямої, кінці якого – основи перпендикулярів, що проведені із початка і кінця вектора на вісь координат, причому із знаком „+” або „-„ в залежності від того, гострий або тупий кут між віссю і вектором.
Кут між вектором і віссю (або між двома векторами) – найменший кут, на який треба повернути вектор, щоб його напрямок співпав з напрямком вісі.
прх( + ) = npx + npх
aх
=
ау
=
a
cos ax + bx = х( + ) - проекція суми векторів на кожну вісь дорівнює сумі проекцій вихідних векторів.
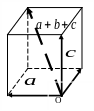
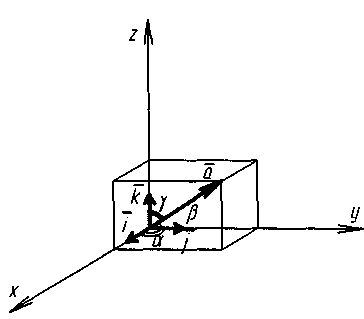
а = ах+ау +аг - диагональ пааллелепипеда,
Проекції
вектора на вісі:
Радіус
– вектор
точки А – це вектор
Розкладання вектора
В просторі
- довільний вектор простору
,
,
Існує завжди розкладання: = α + β + γ
Скалярний добуток векторів
1)
2)
3)
Властивості:
1)
2)
3)
4)
5) Умова перпендикулярності:
6) Умова паралельності:
Скалярний добуток використовується для знаходження кута між векторами:
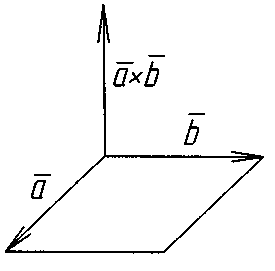
Векторний добуток векторів
Df
Векторний
добуток
двох векторів
–
це
інший вектор
,
перпендикулярний площині, що утримує
вектори
1)
Довжина
дорівнює
добутку
довжин
векторів
2) Вектор векторного добутку =
перпендикулярний
обом векторам
3)
спрямований
так,
що
вектори
Властивості:
|
|
Векторний
добуток використовується для обчислення
площі паралелограма побудованого
на двох неколінеарних векторах:
|
|
Умова колінеарності:
=
0
,
Вектор, перпендикулярний до площини, в якій розташовані , спрямований в сторону, суміщення одного вектора з другим буде здаватися минаючим проти годинникової стрілки (величина його чисельно дорівнює площі паралелограма на векторах). |
Трійка векторів – три вектора, для яких визначений порядок наступності.
Трійка
некомпланарних векторів
трійка
|
Змішаний добуток трьох векторів:
це скалярно - векторний добуток трійки векторів. ( )∙
Результат
скалярного
множення
векторного
добутку
двох векторів на
третій.
,
,
(
)∙
=
Властивості:
1. Порядок множників важливий: при круговій перестановці векторів їх добуток незмінний, при перестановці двох множників – змінює знак на протилежний.
2.
Умова компланарності:
є
ортогональним площині векторів
,
тобто
3. = 0, якщо хоча б один вектор дорівнює нулю.
4.
=
Праві системи координат – системи, базисні вектори яких утворюють праву трійку. |
Геометричний сенс:
|
Змішаний добуток використовується для обчислення об’єму паралелепипеда, побудованого на трьох некомпланарних векторах.
|
Рівняння лінії на площині – це рівняння із змінними х та у, якому задовольняють координати будь-якої точки цієї лінії і не задовольняють координати точки, що не належить лінії.
Найпростіша лінія на площині – пряма.
Вектор, що не дорівнює 0, спрямований вздовж прямой – (т,п) - її направляючий вектор.
Вид рівняння
1.
2. ах + bу + с = 0
3.
4.
5.
6. у – у0 = k(х – х0) пучок прямих М0 – центр пучка
7. у = kх + b
8.
9.
Рівняння лінії в просторі – це рівняння із змінними х, у, z, якому задовольняють координати будь-якої точки цієї лінії і не задовольняють координати точки, що не належить площині.
Вид рівняння
1.
2. ах + bу + сz + d = 0
3.
4.
=
5.
6.
7. а1 х + b1 у + с1 z + d 1 + + (а2х + b2у+ с2z + d2)= 0
Вид рівняння
1.
2. Ах + Ву + Сz + D = 0
3.
4.
5.
6.
7.
|
ПРЯМА НА ПЛОЩИНІ
Пряма на площині визначається точкою та напрямком.
Напрямок задається:
1)
Нормальним
вектором
2)
Напрамляючим
вектором
Назва та позначення
Рівняння
прямої, що проходе через
точку
Загальне рівняння прямої, де а,b – координати перпендикуляра до прямої.
Канонічне рівняння прямої.
Рівняння
прямої, що проходе через
дві
точки
Рівняння прямої в відрізках. На
вісі ОХ відрізок а*=
Рівняння
прямої, що проходе через
точку
з
кутовим коефіцієнтом
Рівняння прямої з кутовим коефіцієнтом , де b – відрізок, який відтинає пряма на вісі ОУ.
Параметрична форма, де t – параметр, , напрамляючий вектор (m,n).
Нормальне
рівняня прямої,
де
Перехід від (2) до (9):
Необходно (2) домножити на
N
= а,b,с
–
числа,
ПРЯМА В ПРОСТОРІ
Пряма в просторі визначається точкою та напрямком. Напрямок задається:
Найпростіша лінія в просторі – пряма.
Назва та позначення
Рівняння
прямої, що проходе через
точку
Загальне рівняння прямої, де а, b, с – координати перпендикуляра до прямої
Канонічне рівняння прямої.
Рівняння
прямої, що проходе через
дві
точки
Параметрична форма, де t – параметр, , напрамляючий вектор (m,n,р).
Векторне рівняня прямої.
Рівняння пучка прямих (через точку перетину двох прямих) з центром в М.
ПЛОЩИНА В ПРОСТОРІ
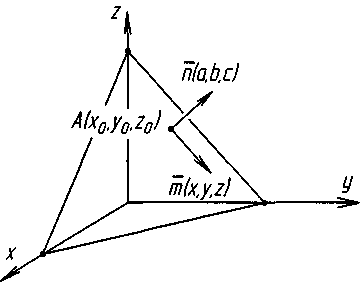
Площина в просторі визначається точкою та напрямком. Напрямок задається нормальним вектором (а,b,с), перпендикулярним до площини.
Назва та позначення
Рівняння прямої, що проходе через точку перепендикулярно нормальному вектору (А,В,С).
Загальне рівняння прямої, де а, b, с – координати перпендикуляра до прямої прямої. У
векторній формі, де
р
–
довжина перпендикуляра із О(0,0,0) на
площину α.
Через норміруючий множник
Рівняння
прямої
в відрізках. На
вісі ОХ відрізок а*=
Рівняння
площини,
що проходе через точку
,
паралельно двом некомпланарним
векторам
Рівняння
площини,
що проходе через 3 точки
,
та
що не належать одній прямій.
|
1. А1 х + В1 у + С1 z + d1 + + (А2х + В2у+ C2z + D2) = 0 Для кожного конкретного це рівняння визначає деяку пряму,що проходе через пряму .
Просторова теорема Піфагора:
2.
3.
4.
Ах + Ву + Сz + D = 0
На площині
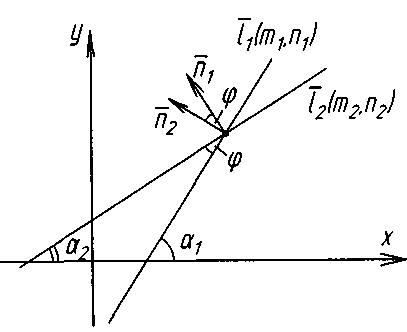
Між
прямими
між
їх нормальними або напрямляючими
векторами:
Якщо
На площині
Прямі:
Якщо
Якщо
На площині
Прямі:
,
то
Якщо
Якщо
,
то
На площині
Від точки до прямої ах + bу + с = 0
Відхилення:
ГМТ – фігура, яка складається із усих точок площини або простора, що мають властивості певні.
Коло- частковий випадок еліпса з рівними осями і фокусами в одній точці – центрі кола.
Фокальні
радіуси
-вектори
(
1)
або 2)
Будуємо
прямокутник
діагоналі - асимптоти, а потім гіперболу, яка перетинає дійсну вісь.
Відстань точки М(х,у) від її фокусів – це фокальні радіус-вектори данної точки.
у2 = 2рх - симетрична відносно ОХ.
х2 = 2qу - симетрична відносно ОУ.
Вершина – в початку системи координат фокальний радіус -вектор.
-
рівняння сфери
з центром С
Приклади: 1.
2.
3.
4.
навколо ОУ). |
ПРЯМА І ПЛОЩИНА У ПРОСТОРІ
Рівняння
пучка площин (через
лінію перетину двох площин)
α2: А2 х + В2у + C2z + D2= 0
Пряма належить площині : Ах + В у + C z + D = 0,
Площина
утримує точку
Нормальний
вектор
Дві прямі належать одній площині
Якщо
Дослідження загального рівняня площини:
1) D = 0 => Ax + By + Cz = 0 – площина проходе через початок координат.
2) A = 0 => By + Cz + D = 0 площина параллельна вісі ОХ.
3) B
= 0
=>
Ax
+ Cz
+ D
= 0
площина
4) C
= 0
=>
Ax
+ By
+ D
= 0
площина
5)
6)
7)
8)
9)
10)
Якщо в рівнянні площини відсутня координата, то площина паралельна цій вісі. КУТИ
У просторі
Між прямими – між їх нормальними або напрямляючими векторами
, .
Між площинами – між їх нормальними векторами: : А1 х + В1 у + C1 z + D1 = 0 α2: А2 х + В2у + C2z + D2 = 0
=
Між прямою та площиною – між прямою і її проекцією на площину.
: Ах + В у + C z + D = 0, .
УМОВА ПАРАЛЕЛЬНОСТІ
У просторі
Прямих:
,
якщо
, . Площин:
: А1 х + В1 у + C1 z + D1 = 0 α2: А2 х + В2у + C2z + D2= 0 Прямої
та площини:
: Ах + В у + C z + D = 0,
УМОВИ ПЕРПЕНДИКУЛЯРНОСТІ
У просторі
Прямі:
,
якщо
, .
Площини:
: А1 х + В1 у + C1 z + D1 = 0 α2: А2 х + В2у + C2z + D2= 0
Прямої
та площини:
,
: Ах + В у + C z + D = 0,
ВІДСТАНЬ
У просторі
Від
точки
до
ах
+ bу + сz + d = 0
прямої.
Від точки до площини :
Ах
+ В
у
+
C
z
+ D
=
0.
Відхилення:
Норміруючий
множник
КРИВІ 2 ПОРЯДКУ
Це лінії, координати точок яких задовольняють рівнянням другого степеня.
Коло
Це
геометричне місце точок площини
(ГМТ), рівновіддалених від однієї
точки – центра.
Коло з центром в початку координат 0(0,0)
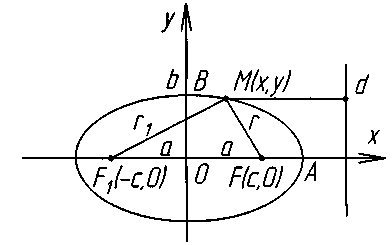
Еліпс
Це геометричне місце точок (ГМТ), сума відстаней яких від двох точок F и f1 (фокусів) є величина постійна. С - центр, а, b – піввісі. а – велика (на ОХ), b – мала (на ОУ).
1)
Якщо
а
>
b,
то
F
и f1
на
вісі
ОХ на відстані
с
=
2)
Якщо а
<
b,
то
F
и f1
на
вісі
ОУ на відстані
с
=
Директриси
еліпса
Ексцентриситет
еліпса
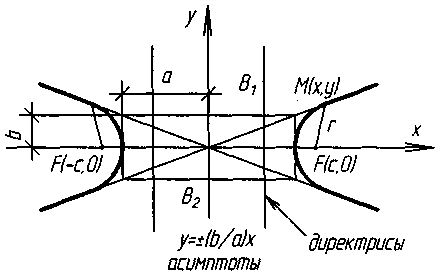
Гіпербола
Це геометричне місце точок площини (ГМТ), різниця відстаней яких від двох даних точок F и f1 (фокусів), є величина постійна: 2а (0 < 2а < FF1). а, b – піввісі.
F(с; о) і f1 (- с; о) - фокуси. |FF1| = 2с.
1)
а – на
дійсній
піввісі ОХ; х =
2)
b
– на
дійсній
піввісі ОУ; вершина гіперболи у =
а
– на
мнімій
піввісі ОХ. с =
с – відстань фокуса від початку координат. а – велика (на ОХ), b – мала (на ОУ). = |- а + х|, = |а + х| - фокальні радіус-вектори асимптоти.
Ексцентриситет
гіперболи
Якщо а = b, то гіпербола рівнобічна х2 - у2 = а2. Асимптоти: у = х, х = у.
Сполучені:
Парабола
Це геометричне місце точок площини, рівновіддалених від данної точки - фокуса і від данної прямой - директриси.
Фокус
не належить директрисі.
Якщо
Директриса
паралельна ОХ, то у =
Якщо
- гілки догори, - гілки донизу.
,
- координати вершини
Директриса паралельна ОУ, то х =
Для визначення геометричного образу, який описує алгебраічне рівняння вигляду
Ах2 + Ву2 + Сх + Dу + F = 0
треба звести його до одного з каноничних рівнянь ліній другого порядку шляхом виділення повних квадратів:
ПОЛЯРНА СИСТЕМА КООРДИНАТ.
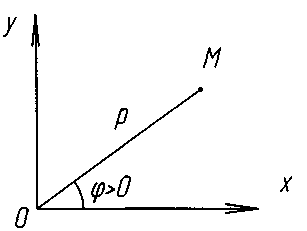
Беремо довільну точку О – полюс та одиницю масштабу. З неї виходе півпряма - полярна вісь. ОР - промінь. Положення точки М на площині визначається двома величинами: 1) р - радіус – вектор > 0, відстань від М до полюса О: ρ = ОМ.
2) φ
– полярний
кут - величина
кута,
утвореного
[ОМ] з
віссю
Якщо
0
Для полюса ρ = 0, кут φ – будь-який.
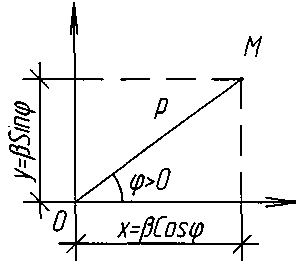
Зв’язок ПОЛЯРНИХ і прямокутних декартових координат.
Відстань
між точками:
Приклади:
1. ρ = а = Const - коло з центром в О і ρ = а, х2+у2 = а2
2. ρ = аφ - спіраль Архимеда.
3. ρ = 2acosφ - коло з центром в точці ρ0 = а, φ = 0, R = a.
4.
5.
ρ
= 2acos
3 6. ρ = a(1 + cosφ) - кардіоіда ПОВЕРХНІ 2 ПОРЯДКУ
Це такі поверхні, рівняння яких містять хоча б одну з координат х, у, z у 2 степені. Конічна – поверхня, яка утворена прямою лінією (твірною), що проходить через задану точку (вершину поверхні) і перетинає задану лінію (напрямну лінію). Циліндрична – поверхня, яка утворена прямою лінією (твірною), що проходить паралельно до заданої прямої L (вісі поверхні) і яка проходить через задану лінію (напрямну лінію).
1.Твірна
паралельна ОZ,
2.
3.
Твірна паралельна ОУ,
4.
Твірна паралельна ОХ,
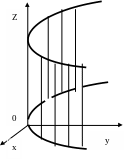
Правило знаходження рівняня проверхні обертання:
незмінною координату, одноіменну з віссю обертання.
обертання
замінити на
Застосовується метод перерізу. Застосування кривих та поверхонь обертання:
радіощогл (однополостні гіперболоіди).
радіолокаторів (параболоіди обертання).
(коло, еліпс, парабола, гіпербола в залежності від швидкості і відстані)… |
Конспект – схема лекції
„Вступ до математичного аналізу”
1. Основні поняття.
2. Множини.
2. Функція однієї змінної.
3. Теорія границь.
5. Неперервність функції.


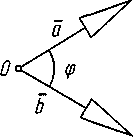
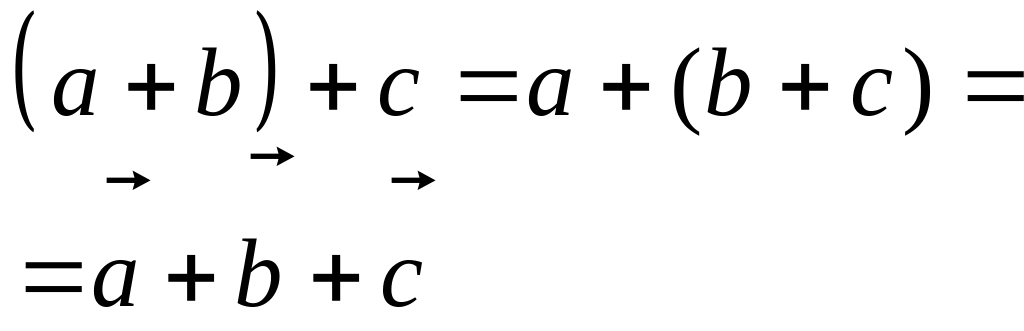
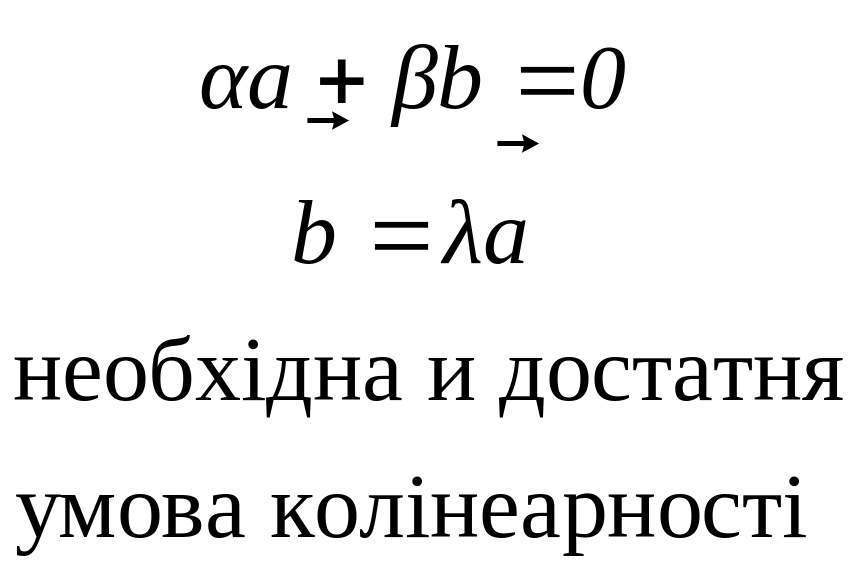

 )
)



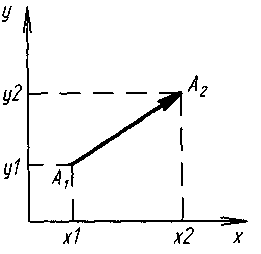
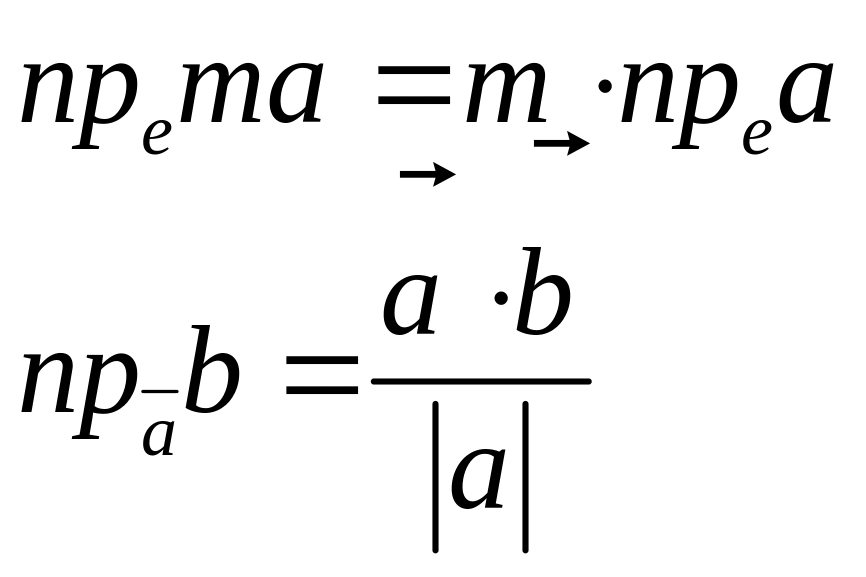




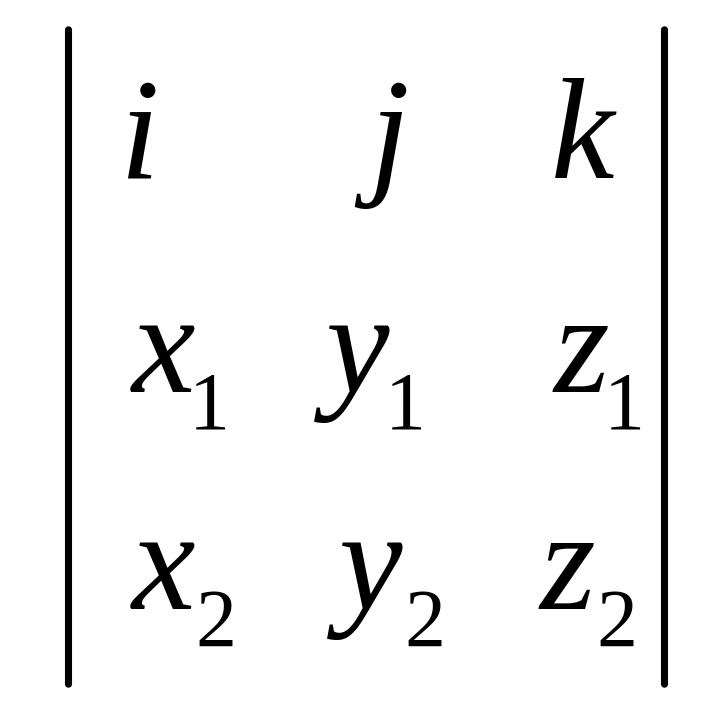 .
.
 ожний
вектор
ожний
вектор
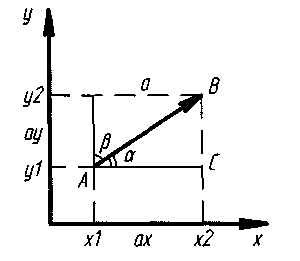
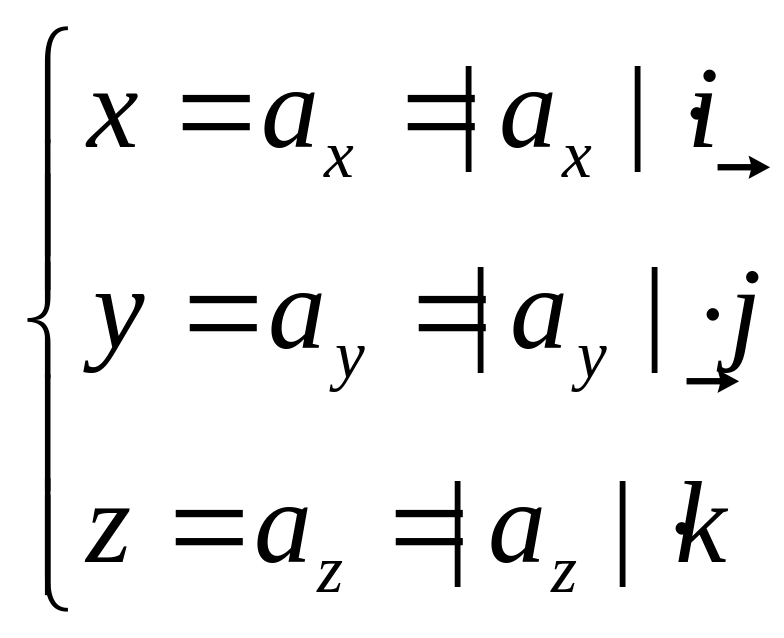
 .
.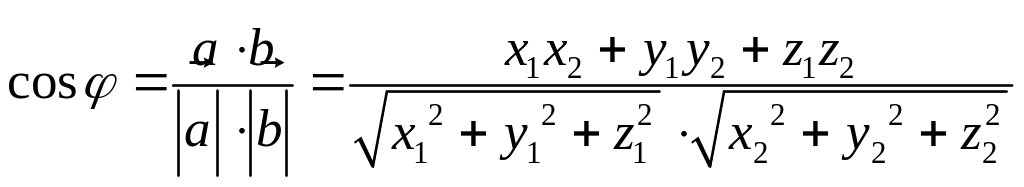
 права
права ліва
ліва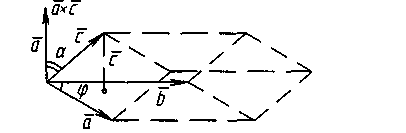
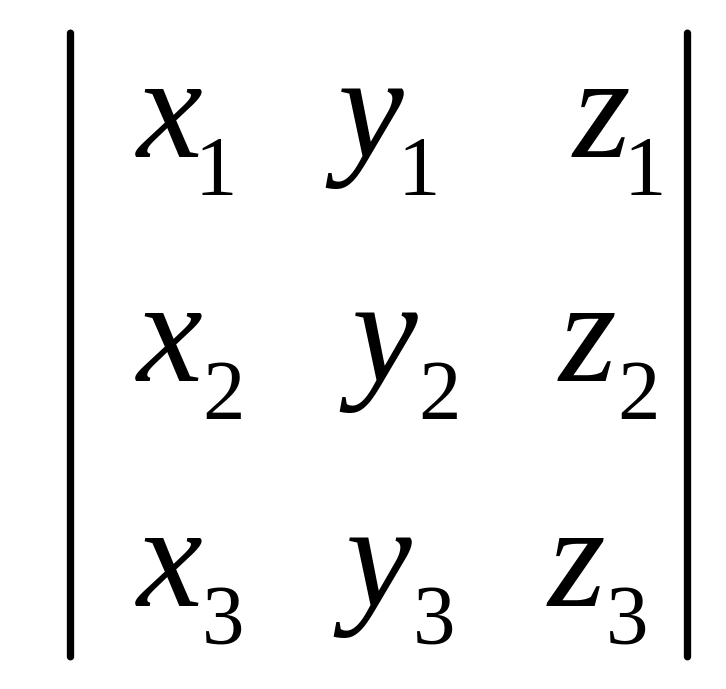 =
=
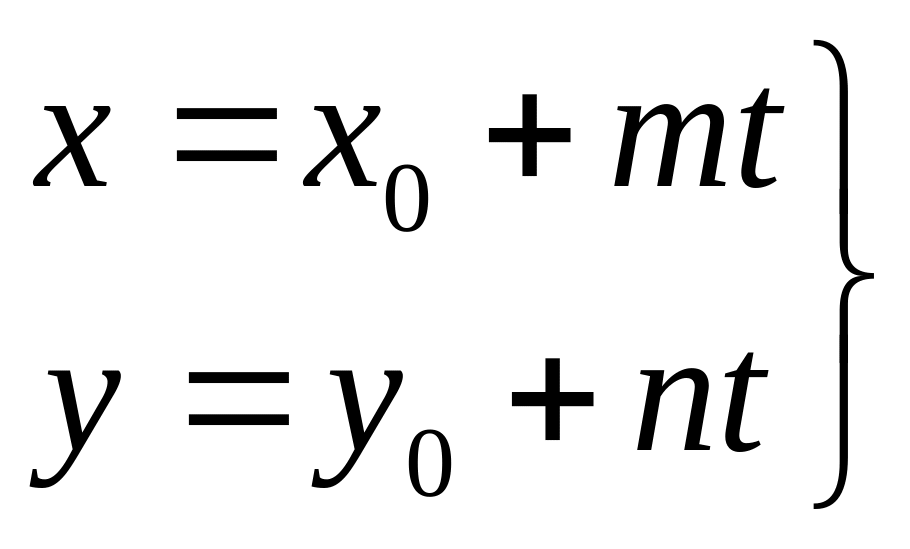
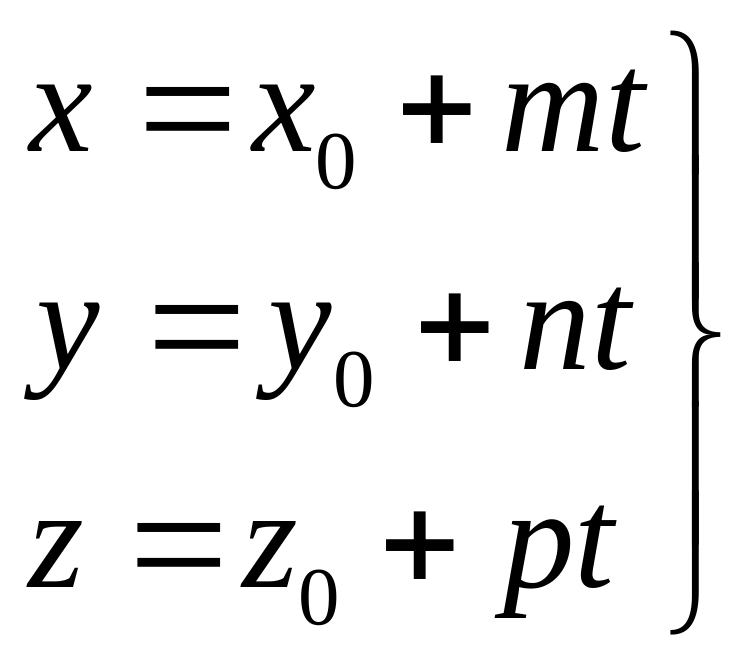
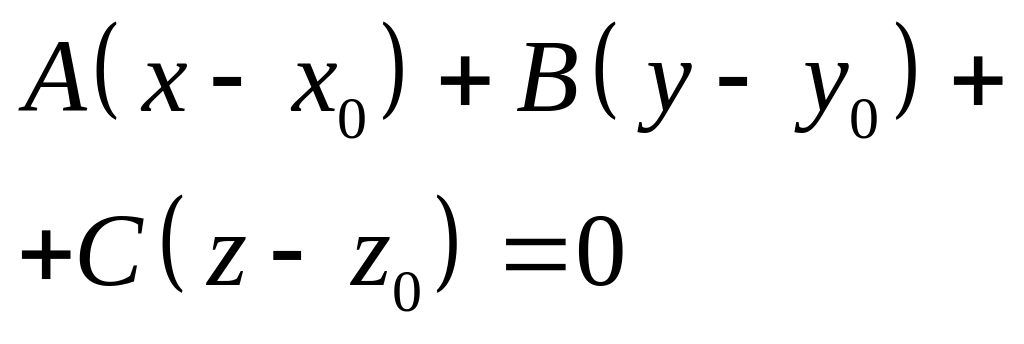
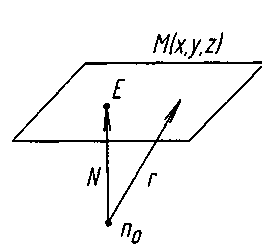
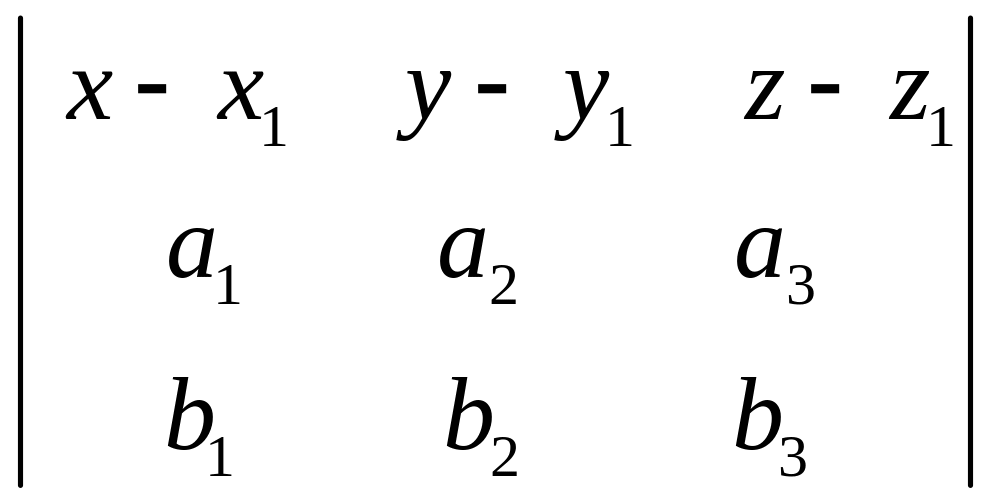 =
0
=
0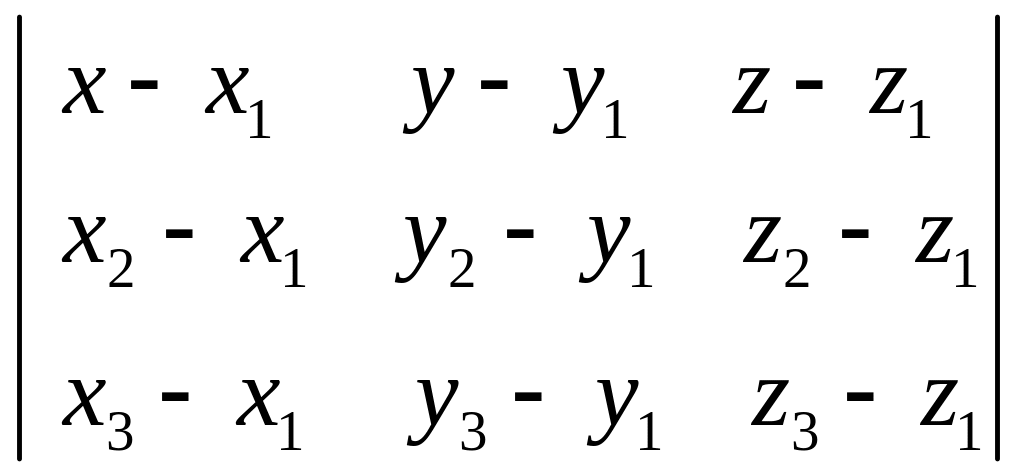 =
0
=
0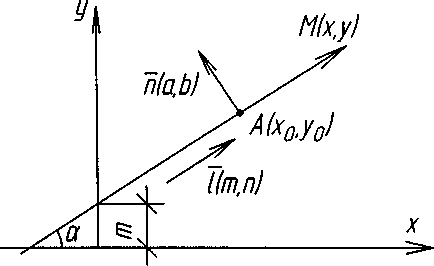
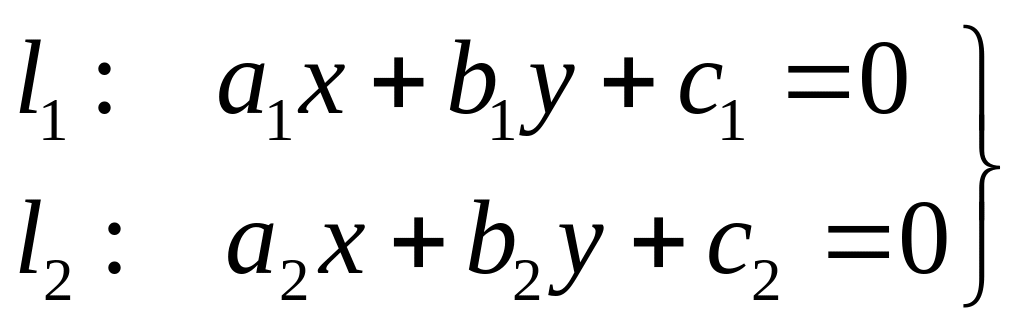
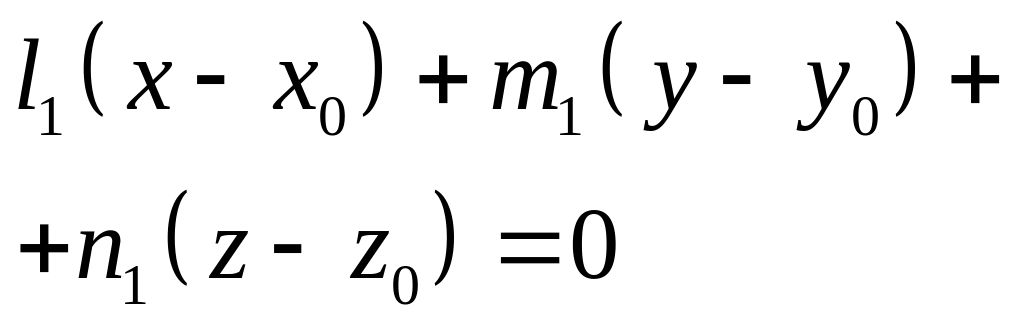
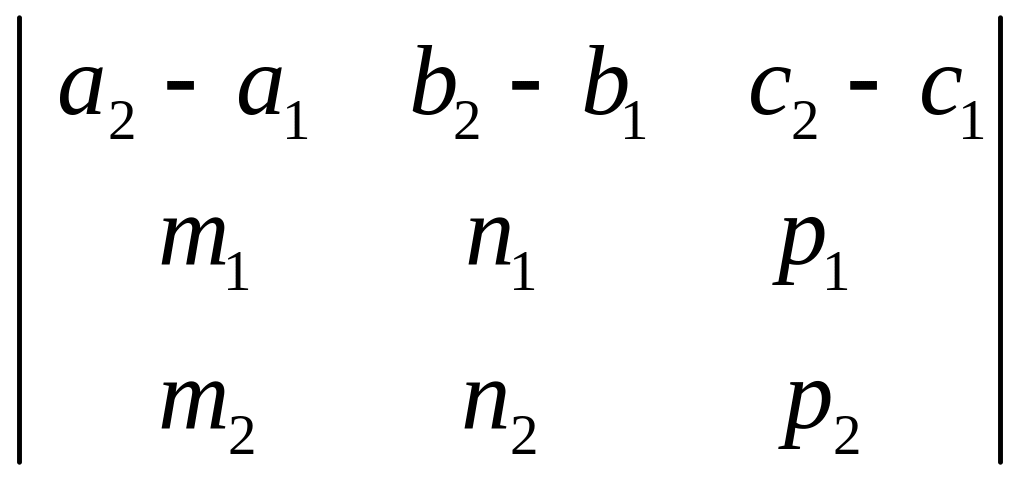 =
0
=
0