
- •І. Загальні положення
- •Уміння, на формування яких націлене навчання:
- •Стисла робоча програма (осінній семестр)
- •Тематика лекцій
- •2.2 Тематика практичних занять
- •Разом: 64 годин
- •Питання для самоперевірки
- •Навчальна література
- •Опорний конспект лекції „Визначники”
- •Характеристики визначників:
- •Властивості визначників:
- •Обчислення визначників
- •Конспект – схема лекції „Матриці”
- •Матриці
- •Характеристики матриць:
- •Властивості матриць:
- •Алгоритми знаходження оберненої матриці:
- •Ранг матриці
- •Методи визначення рангу матриць
- •Властивості рангу матриць:
- •Лінійна залежність
- •Конспект – схема лекції
- •Лінійні рівняння
- •Системи лінійних рівнянь
- •Види систем:
- •Елементарні перетворення системи
- •Критерій сумісності системи рівнянь
- •Методи розв’язання систем
- •Конспект – схема лекцій з
- •Вектори
- •Основні поняття
- •Характеристики змінних величин
- •Множини.
- •Дії над множинами
- •Область визначення (існування) функції – одз
- •Характеристики функцій:
- •Теорія границь
- •Означення границі
- •Властивості границь
- •Основні теореми про границі функцій
- •Нескінченно малі та нескінченно великі
- •Властивості еквівалентних функцій
- •Обчислення границь
- •Неперервність функцій
- •Точки розриву функції
- •Класифікація точок розриву
- •Правила відшукання точок розриву:
- •Модуль №1. Елементи лінійної алгебри
- •3.1.2. Практичні заняття
- •Методи цілеспрямованого формування у студентів уміння
- •Аналіз конкретних ситуацій.
- •Метод еврестичного дослідження (когнітивний).
- •11. Проблемний метод.
- •3.2. Види організації самостійної роботи, що виконуються студентами у позаурочний час.
- •Самостійні домашні роботи
- •Корекція самостійної роботи
- •Атестаційне тестування
- •Тест № 1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 7
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •1.Визначте вид матриці (прямокутна , квадратна другого порядку, діагональна третього порядку, одинична третього порядку, нульова , матриця-стовпець, матриця-рядок):
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест № 1
- •Тест № 6
- •Тест № 7
- •5. Знайти геометричне місце точок, рівновіддалених від точок :
- •Тест № 8
- •Тест № 9
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест №1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 15
- •Тест № 16
- •Тест № 17
- •Тест № 19
- •Тест № 20
- •Тест № 21
- •Тест № 22
- •2. Встановити, якою є функція (неперервною чи розривною)
- •Тест № 23
- •Тест № 24
- •Тест № 26
- •Тест № 27
- •Тест № 28
- •Тест № 29
- •Завдання 2.
- •Завдання 3.
- •2) По правилу трикутника:
- •3) По правилу Саруса:
- •4) Штучного доповнення:
- •Завдання 6.
- •Завдання 7.
- •Завдання 8.
- •Завдання 9.
- •Завдання 10.
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Додаток 3. Допуск (перевірка готовності) до лекцій:
- •Тема „Матриці”
- •Тема „Системи лінійних алгебраічних рівнянь”
Тест № 8
Продовжить формулювання: „Функція називається неперервною справа (зліва) в точці , якщо ..”.
Встановити, якою є функція
 (неперервною
чи розривною) для кожного з заданих
значень аргументу
(неперервною
чи розривною) для кожного з заданих
значень аргументу
 .
.при х=3 функція неперервна, х=4 – розрив ІІ-го роду.
при х=4 функція неперервна, х=3 – розрив ІІ-го роду.
при х=4 функція неперервна, х=3 – розрив І-го роду.
при х=3, х=4 – розриви ІІ-го роду.
3. Обчислити границі з невизначеністю типу та :
а)
 б)
б)

1. а)
|
2. а)
|
3. а)
|
4.Інша відповідь |
4. Обчислити границі
із застосуванням першої та другої
цікавих границь а)
![]() ;
б)
;
б)
![]()
1.а)
|
2.а) 1; б) |
3. а)
;
б)
|
4.Інша відповідь |
Тест № 9
Продовжить формулювання:
„Точка називається точкою усуненого розриву, що функції , якщо ..”.
Встановити, якою є функція
 (неперервною
чи розривною) для кожного з заданих
значень аргументу
(неперервною
чи розривною) для кожного з заданих
значень аргументу
 .
.при х=-3 функція неперервна, х=1 – розрив ІІ-го роду.
при х=1 функція неперервна, х=-3 – розрив І-го роду.
при х=1 , х=-3 – розриви ІІ-го роду.
при х=1 функція неперервна, х=-3 – розрив ІІ-го роду.
3. Обчислити границі з невизначеністю типу та :
а)
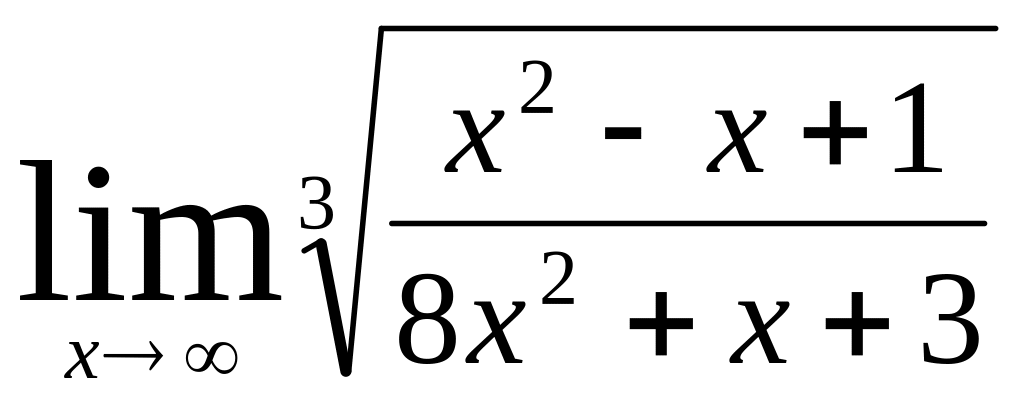 ;
б)
;
б)
![]()
|
2. а)
;
б)
|
3. а)
|
4. Інша відповідь |
4. Обчислити границі
із застосуванням першої та другої
цікавих границь а)
![]() ;
б)
;
б)
![]()
1. а)
|
2. а) ; б) |
3. а)
1; б)
|
4.Інша відповідь |
Тест № 10
1.
Продовжить твердження: „Границя
функції
![]() в точці
в точці
![]() ..”.
..”.
2.
Встановити, якою є функція
![]() (неперервною
чи розривною) для кожного з заданих
значень аргументу
(неперервною
чи розривною) для кожного з заданих
значень аргументу
![]() .
.
при х=5 функція неперервна, х=1 – розрив ІІ-го роду.
при х=1 функція неперервна, х=5 – розрив І-го роду.
при х=1 функція неперервна, х=5 – розрив ІІ-го роду.
при х=1 , х=5 – розриви ІІ-го роду.
3. Обчислити границі з невизначеністю типу та :
а)
 ;
б)
;
б)
![]()
1.а)
|
2.а) ; б) 1 |
3.а) |
4.Інша відповідь |
4. Обчислити границі
із застосуванням першої та другої
цікавих границь а)
![]() ;
б)
;
б)
![]()
1. а) -6; б) |
2. а) -5; б) |
3. а) ; б) |
4. Інша відповідь |
Тест № 11
1.Продовжить
твердження: „Границя
функції
![]() при
при
![]() існує.
існує.
2.
Встановити, якою є функція
![]() (неперервною
чи розривною) для кожного з заданих
значень аргументу
(неперервною
чи розривною) для кожного з заданих
значень аргументу
![]() .
.
при х=5 функція неперервна, х=-3 – розрив ІІ-го роду.
при х=-3 функція неперервна, х=5 – розрив І-го роду.
при х=-3 функція неперервна, х=5 – розрив ІІ-го роду.
при х=-3 , х=5 – розриви ІІ-го роду.
3. Обчислити границі з невизначеністю типу та :
а)
 ;
б)
;
б)
![]()
1. а)1; б) |
2. а) ; б) 1 |
3. а)
|
4. Інша відповідь |
4.
Обчислити границі із застосуванням
першої та другої цікавих границь а)
![]() ;
б)
;
б)
![]()
|
2.а) 5;
б)
|
3.а) ; б) |
4.Інша відповідь |
