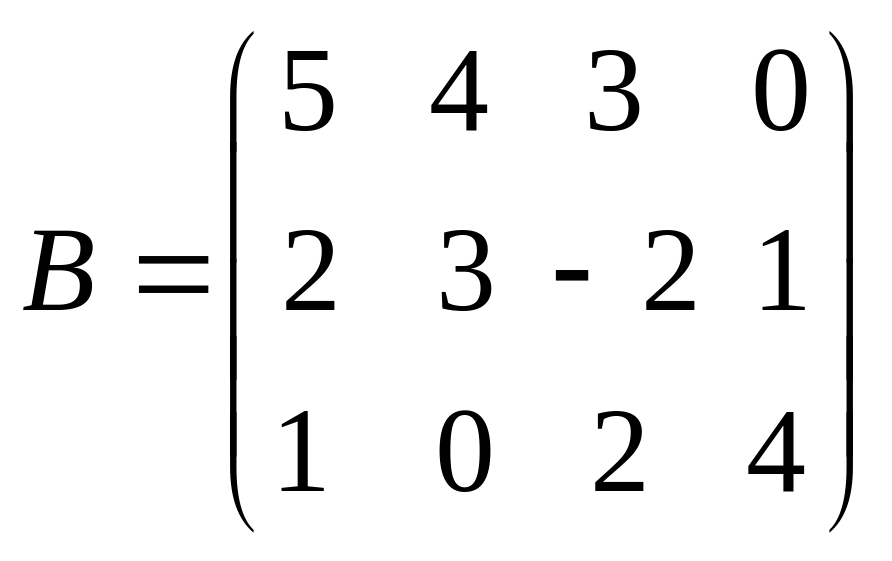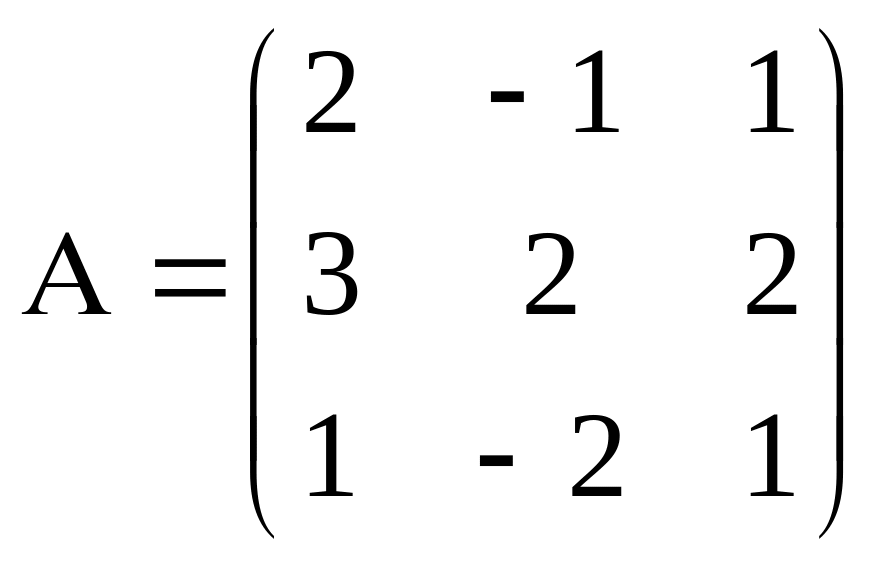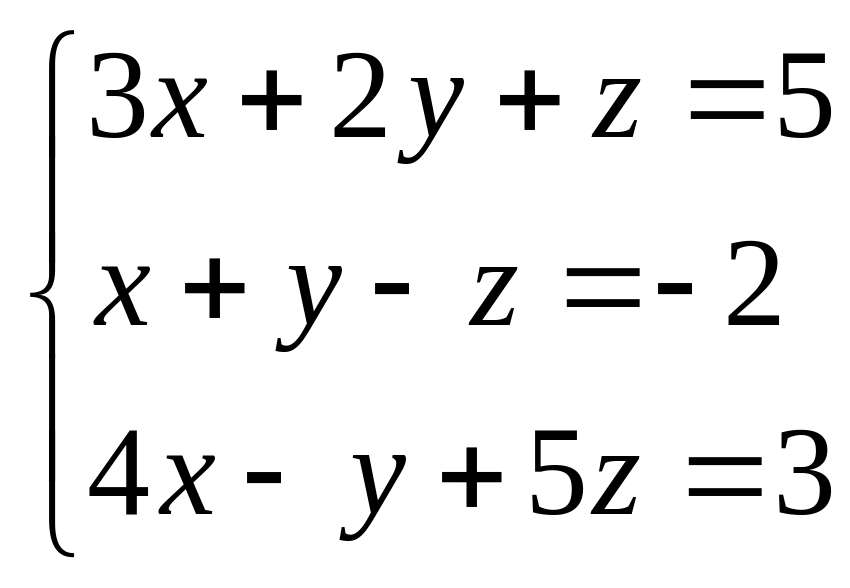- •І. Загальні положення
- •Уміння, на формування яких націлене навчання:
- •Стисла робоча програма (осінній семестр)
- •Тематика лекцій
- •2.2 Тематика практичних занять
- •Разом: 64 годин
- •Питання для самоперевірки
- •Навчальна література
- •Опорний конспект лекції „Визначники”
- •Характеристики визначників:
- •Властивості визначників:
- •Обчислення визначників
- •Конспект – схема лекції „Матриці”
- •Матриці
- •Характеристики матриць:
- •Властивості матриць:
- •Алгоритми знаходження оберненої матриці:
- •Ранг матриці
- •Методи визначення рангу матриць
- •Властивості рангу матриць:
- •Лінійна залежність
- •Конспект – схема лекції
- •Лінійні рівняння
- •Системи лінійних рівнянь
- •Види систем:
- •Елементарні перетворення системи
- •Критерій сумісності системи рівнянь
- •Методи розв’язання систем
- •Конспект – схема лекцій з
- •Вектори
- •Основні поняття
- •Характеристики змінних величин
- •Множини.
- •Дії над множинами
- •Область визначення (існування) функції – одз
- •Характеристики функцій:
- •Теорія границь
- •Означення границі
- •Властивості границь
- •Основні теореми про границі функцій
- •Нескінченно малі та нескінченно великі
- •Властивості еквівалентних функцій
- •Обчислення границь
- •Неперервність функцій
- •Точки розриву функції
- •Класифікація точок розриву
- •Правила відшукання точок розриву:
- •Модуль №1. Елементи лінійної алгебри
- •3.1.2. Практичні заняття
- •Методи цілеспрямованого формування у студентів уміння
- •Аналіз конкретних ситуацій.
- •Метод еврестичного дослідження (когнітивний).
- •11. Проблемний метод.
- •3.2. Види організації самостійної роботи, що виконуються студентами у позаурочний час.
- •Самостійні домашні роботи
- •Корекція самостійної роботи
- •Атестаційне тестування
- •Тест № 1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 7
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •1.Визначте вид матриці (прямокутна , квадратна другого порядку, діагональна третього порядку, одинична третього порядку, нульова , матриця-стовпець, матриця-рядок):
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест № 1
- •Тест № 6
- •Тест № 7
- •5. Знайти геометричне місце точок, рівновіддалених від точок :
- •Тест № 8
- •Тест № 9
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест №1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 15
- •Тест № 16
- •Тест № 17
- •Тест № 19
- •Тест № 20
- •Тест № 21
- •Тест № 22
- •2. Встановити, якою є функція (неперервною чи розривною)
- •Тест № 23
- •Тест № 24
- •Тест № 26
- •Тест № 27
- •Тест № 28
- •Тест № 29
- •Завдання 2.
- •Завдання 3.
- •2) По правилу трикутника:
- •3) По правилу Саруса:
- •4) Штучного доповнення:
- •Завдання 6.
- •Завдання 7.
- •Завдання 8.
- •Завдання 9.
- •Завдання 10.
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Додаток 3. Допуск (перевірка готовності) до лекцій:
- •Тема „Матриці”
- •Тема „Системи лінійних алгебраічних рівнянь”
11. Проблемний метод.
3.2. Види організації самостійної роботи, що виконуються студентами у позаурочний час.
Самостійні домашні роботи
Кожний студент отримує індивідуальний варіант роботи, іноді поетапно. Завдання відповідають змісту модулів і розраховані на відпрацювання певних математичних операцій і дій, на закріплення означень і понять, властивостей і особливостей, а також мають місце і завдання творчого характеру. Після перевірки робіт, студенти мають можливість покращати результати шляхом роботи над помилками самостійно або за допомогою товаришів, які при умові позитивного результату теж отримують заохочуючу оцінку.
№ |
ДЗ №1 |
ДЗ №2 |
ДЗ №3 |
1. |
Навести конкретні приклади до усих властивостей визначників і довести їх. |
1.Дани
координати вершин піраміди
|
1. Визначити ОДЗ функції: а)
|
2. |
Довести властивість 9 для будь-яких стовпців (рядків) в загальному вигляді. |
Знайти: 1)довжину ребра АВ. |
б)
с)
|
3. |
Обчислити визначник (по будь-якому рядку(стовпцю) штучного доповнення, правило трикутника, правило Сарюса) - 4
способами:
|
2)Кут між ребрами АВ і АД.
3) Кут між ребром АД і гранню АВС.
4)Кут між гранями АВС та АДС. |
2. Обчислити границі: 1)
2)
3)
|
4. |
Обчислити визначник будь-яким способом:
|
5) Площу грані АВС.
6) Об’єм піраміди.
7) Довжину висоти із Д на грань АВС. |
4)
5)
6)
|
5. |
Розв’язати нерівність:
|
8) Проекцію точки Д на грань АВС. Рівняння прямих: 9) Через вершину |
7)
8)
|
6. |
Знайти А·В та В·А, якщо: А= |
С паралельно АД -ребру.
10) Через точку В перпендикулярно грані АДС. |
9)
10)
|
7. |
Знайти
ранг матриці двома способами: А= |
11) Скласти рівняння площини, що проходе через вершину С, перпендикулярно |
3. Визначити неперервність функції: |
8. |
Розв’язати рівняння: 5А
+ 2Х – В = 0, якщо
|
ребру АВ.
12) Побудувати піраміду в просторі. |
1)
в точках х = 1 та х = 2.
|
9. |
Знайти обернену матрицю двома способами:
|
2. Визначити та побудувати лінію, рівняння якої має вигляд:
|
2)
f(x) = = |
10 |
Розв’язати систему лінійних алгебраічних рівнянь 3 способами (метод Гауса, правило Крамера, за допомогою оберненої матриці):
|
3.
Дослідити лінійну залежність векторів:
|
|
4.Скласти рівняння ГМТ, для яких сума відстаней до точок А(2;3) і В(4;5)дорівнює 54.
|


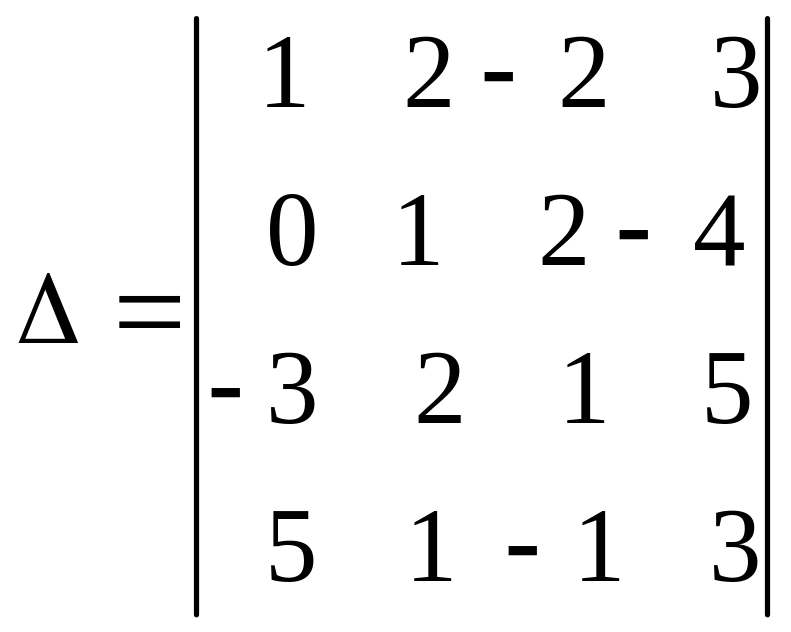
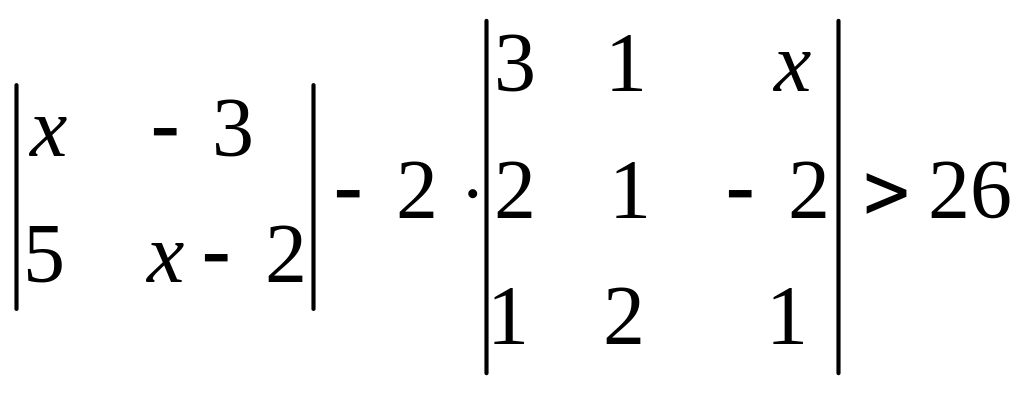
 ,
В =
,
В =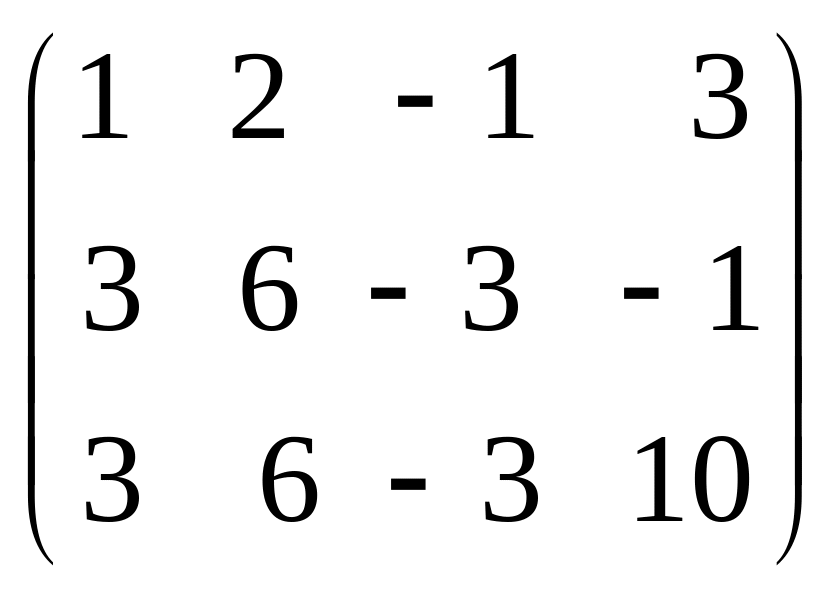
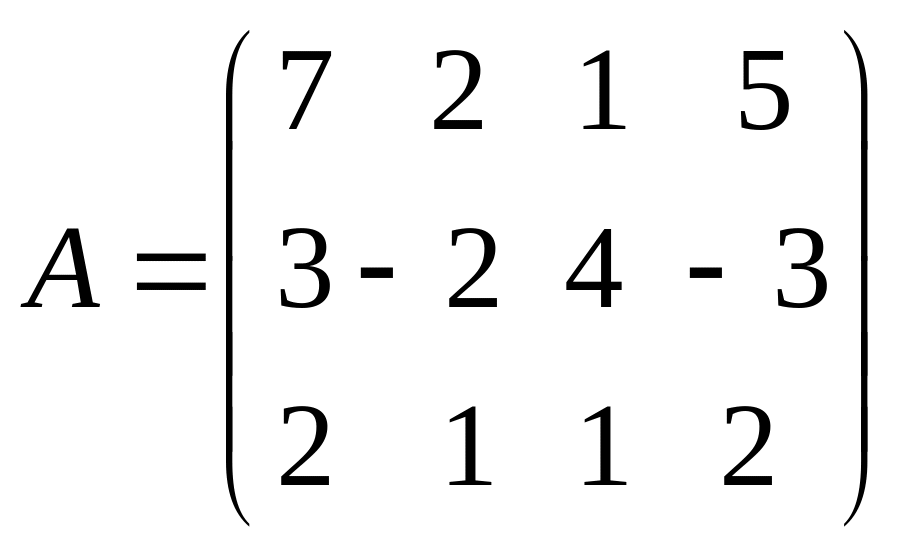 ,
,