
- •І. Загальні положення
- •Уміння, на формування яких націлене навчання:
- •Стисла робоча програма (осінній семестр)
- •Тематика лекцій
- •2.2 Тематика практичних занять
- •Разом: 64 годин
- •Питання для самоперевірки
- •Навчальна література
- •Опорний конспект лекції „Визначники”
- •Характеристики визначників:
- •Властивості визначників:
- •Обчислення визначників
- •Конспект – схема лекції „Матриці”
- •Матриці
- •Характеристики матриць:
- •Властивості матриць:
- •Алгоритми знаходження оберненої матриці:
- •Ранг матриці
- •Методи визначення рангу матриць
- •Властивості рангу матриць:
- •Лінійна залежність
- •Конспект – схема лекції
- •Лінійні рівняння
- •Системи лінійних рівнянь
- •Види систем:
- •Елементарні перетворення системи
- •Критерій сумісності системи рівнянь
- •Методи розв’язання систем
- •Конспект – схема лекцій з
- •Вектори
- •Основні поняття
- •Характеристики змінних величин
- •Множини.
- •Дії над множинами
- •Область визначення (існування) функції – одз
- •Характеристики функцій:
- •Теорія границь
- •Означення границі
- •Властивості границь
- •Основні теореми про границі функцій
- •Нескінченно малі та нескінченно великі
- •Властивості еквівалентних функцій
- •Обчислення границь
- •Неперервність функцій
- •Точки розриву функції
- •Класифікація точок розриву
- •Правила відшукання точок розриву:
- •Модуль №1. Елементи лінійної алгебри
- •3.1.2. Практичні заняття
- •Методи цілеспрямованого формування у студентів уміння
- •Аналіз конкретних ситуацій.
- •Метод еврестичного дослідження (когнітивний).
- •11. Проблемний метод.
- •3.2. Види організації самостійної роботи, що виконуються студентами у позаурочний час.
- •Самостійні домашні роботи
- •Корекція самостійної роботи
- •Атестаційне тестування
- •Тест № 1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 7
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •1.Визначте вид матриці (прямокутна , квадратна другого порядку, діагональна третього порядку, одинична третього порядку, нульова , матриця-стовпець, матриця-рядок):
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест № 1
- •Тест № 6
- •Тест № 7
- •5. Знайти геометричне місце точок, рівновіддалених від точок :
- •Тест № 8
- •Тест № 9
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 14
- •Тест № 15
- •Тест №1
- •Тест № 2
- •Тест № 3
- •Тест № 4
- •Тест № 5
- •Тест № 6
- •Тест № 8
- •Тест № 9
- •Тест № 10
- •Тест № 11
- •Тест № 12
- •Тест № 13
- •Тест № 15
- •Тест № 16
- •Тест № 17
- •Тест № 19
- •Тест № 20
- •Тест № 21
- •Тест № 22
- •2. Встановити, якою є функція (неперервною чи розривною)
- •Тест № 23
- •Тест № 24
- •Тест № 26
- •Тест № 27
- •Тест № 28
- •Тест № 29
- •Завдання 2.
- •Завдання 3.
- •2) По правилу трикутника:
- •3) По правилу Саруса:
- •4) Штучного доповнення:
- •Завдання 6.
- •Завдання 7.
- •Завдання 8.
- •Завдання 9.
- •Завдання 10.
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Розв’язання:
- •Додаток 3. Допуск (перевірка готовності) до лекцій:
- •Тема „Матриці”
- •Тема „Системи лінійних алгебраічних рівнянь”
Методи розв’язання систем
Назва, сутність |
Формули та пояснення |
Пекреваги та недоліки |
Метод Гауса – метод послідов-ного виключен-ня невідомих |
Елементарними перетвореннями система зводиться до еквівалентної ступінчатого виду (трикутного або трапеціідального):
Існує 3 способа:
через інші і підставляють його в інші рівняння, доки не отримають 1 рівняння з 1 невідомим.
допомогою розширеної матриці системи, зводячи її поступово до діагональної матриці.
приравнюючи коефіцієнти при 1 з невідомих і потім складаючи або віднімаючи одне рівняння з іншим (2 рази почленно).
|
Переваги:
1. Можливість використовувати при розв’язанні і однорідних, і неоднорідних систем з будь- яким співвідношенням числа невідомих і числа рівнянь. 2. Система легко піддається дослідженню. 3. Не треба попередньо досліджувати умову сумісності системи рівнянь.
Недоліки: немає |
Різновиди метода Гауса |
1. Метод головних елементів – якщо система розв’язується наближено (на кожному кроці вибирають головний елемент - найбільший по модулю в підсистемі коефіцієнт). 2. Метод Жордано - Гауса – метод повного виключення ведучого невідомого на кожному кроці з рівнянь підсистеми і з ведучих рівнянь попередніх кроків.
|
Недолік: Великий обсяг роботи.
Переваги: Можна розв’язувати системи з багатьма невідомими. |
Метод Крамера – складання і обчис-лення 4 визначни-ків |
∆= головний Допоміжні: ∆х
= ∆z
= Висновок: 1)
2) ∆ = 0, а хоча б 1 з ∆і 0 рішень немає. 3) ∆ = 0, ∆і = 0 система сумісна або має безліч рішень.
|
Недолік:
Лише для систем n лінійних рівнянь з n невідомими. |
За допо-могою оберненої матриці – розв’язан-ня матрич-ного рівняння |
А-1 = = , =
|
Недолік: Труднощі - в знаходженні оберненої матриці, якщо n > 3. Лише для систем n лінійних рівнянь з n невідомими. |

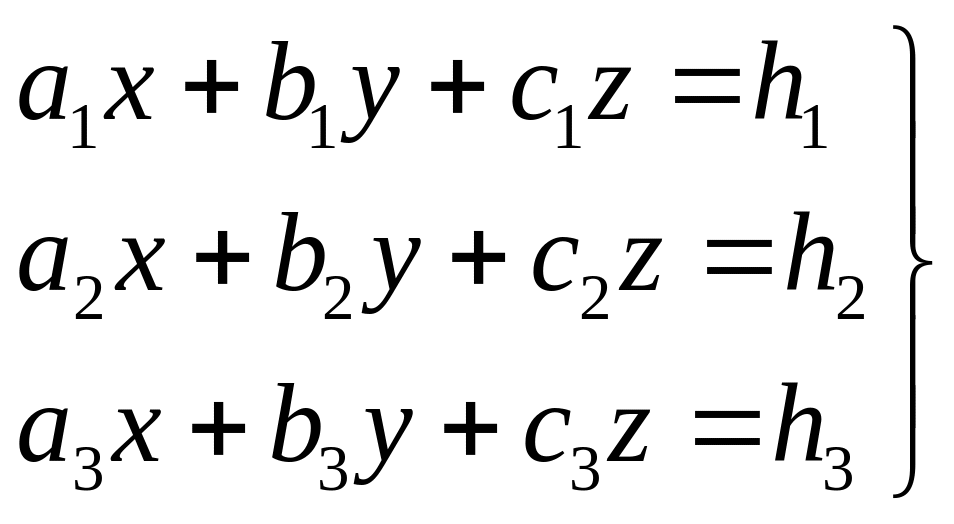
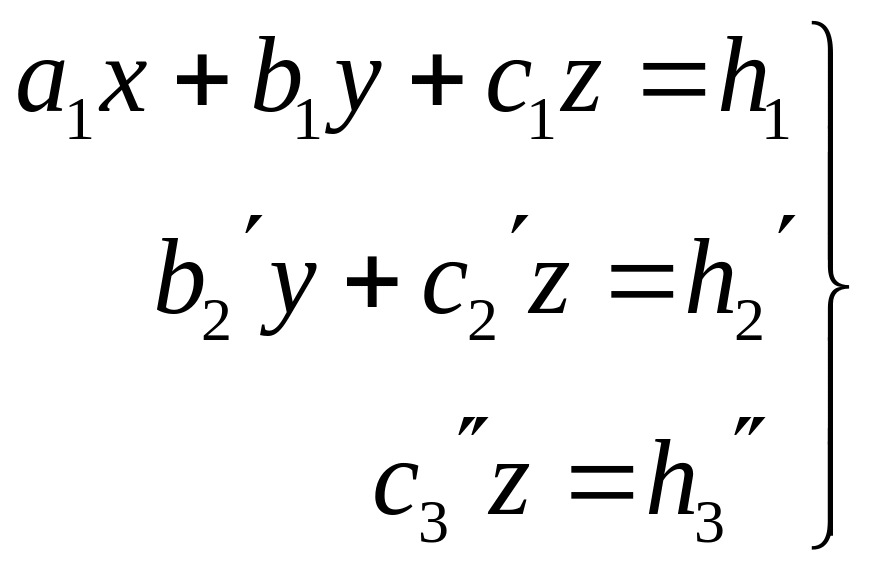
 ,
∆у
=
,
∆у
=
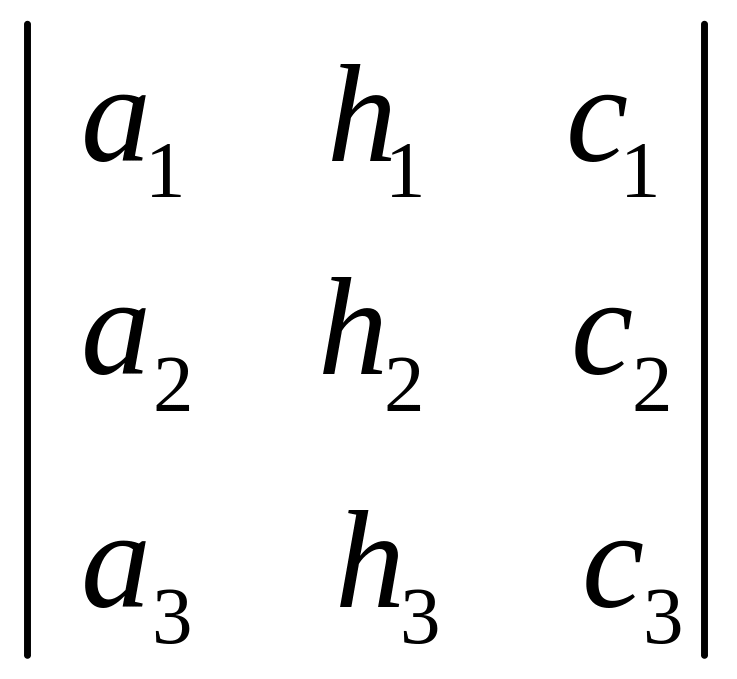
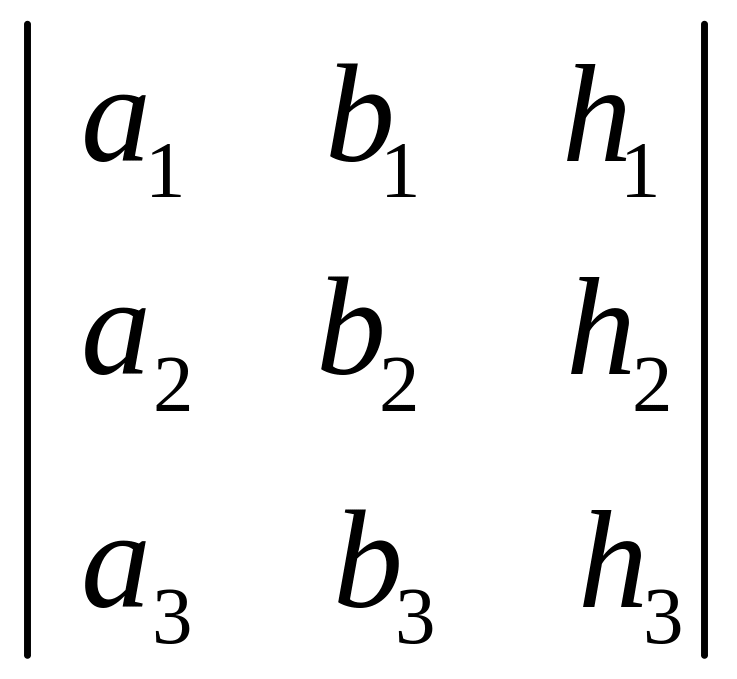 .
х =
.
х =
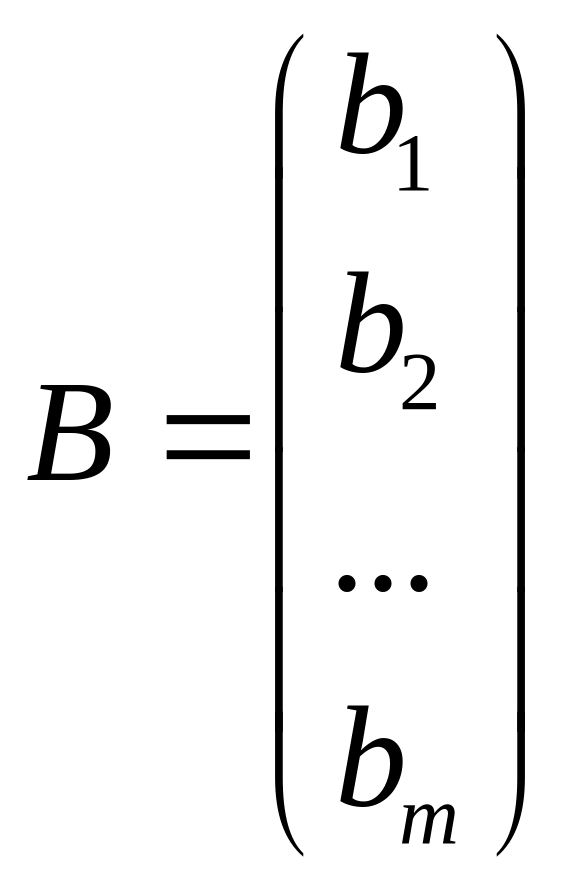 ,
,
 ,
АХ = В, Х = А-1В,
,
АХ = В, Х = А-1В,