13.2. Количественные характеристики размеров макромолекул

Благодаря гибкости и тепловому движению сегментов макромолекула принимает в растворе множество конформаций. Конформацией называется пространственное расположение атомов в молекуле. Охарактеризовать каждую из этих конформаций нельзя, но, так как конформаций бесчисленной множество, для их характеристики можно применить статистические методы, теорию вероятностей. Применение статистических методов к гибкой макромолекуле позволяет охарактеризовать ее средние размеры двумя геометрическими параметрами: среднеквадратичным расстоянием между концами и средним радиусом инерции (рис. 13.3). Возьмем некоторый контур, разобьем его на произвольное число равных элементов, и из центра инерции 0 проведем радиусы к середине каждого отрезка. Легко видеть, что , где – число сегментов. Среднеквадратичное расстояние между концами цепи характеризует степень свернутости макромолекулы. При большом значении макромолекула сильно вытянута, тогда как при малом значении макромолекула сильно свернута.

Рис. 13.3. ( ) - Среднеквадратичное расстояние между концами цепи; (б) средний радиус инерции макромолекулы.

13.3. Свойства Гауссова клубка

Набор конформаций гибкой макромолекулы в растворе характеризуется гауссовой функцией распределения расстояний между концами цепи: (рис. 13.4.).

означает вероятность конформации с расстоянием между концами цепи. Согласно формуле Гаусса, эта вероятность определяется выражением:

(13.3)

Рис. 13.4. Распределение макромолекул по среднеквадратичным расстояниям между концами цепи.

Анализ этой функции показывает, что сильно свернутые конформации с малым мало вероятны. То же самое можно сказать о сильно вытянутых конформациях со средним значение .

Молекулярный клубок, характеризующийся гауссовой функцией распределения расстояния между концами цепи, называется гауссовым клубком. Гауссов клубок обладает еще одним свойством, описываемым гауссовой функцией. Плотность сегментов в клубке максимальна в центре, и убывает к периферии и характеризуется гауссовой функцией распределения по радиусу инерции (рис. 13.5).

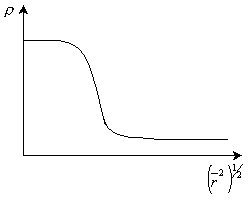
Рис.13. 5. Функция распределения плотности сегментов по радиусу инерции.

Таким образом, гауссов клубок – это облако сегментов, распределенных вокруг центра инерции по гауссову закону. Гауссов клубок имеет форму эллипсоида вращения, близкого к бобу. Следовательно, гауссова функция описывает как множество клубков (по распределению расстояний между концами цепи), так и отдельный клубок (по распределению плотности сегментов относительно центра инерции)

Статистическая теория приводит к простым соотношениям между параметрами, характеризующими размеры цепи, и величиной сегмента: . Если полную контурную длину цепи обозначить через , то и ; .

Эти соотношения справедливы для линейных цепей с гауссовым распределением звеньев при условии .

13.4. Состояния полимеров в растворе

Если минимально различимые детали цепи много меньше персистентной длины, то фотографии участка полимерной цепи, сделанные при разном увеличении, будут выглядеть похожими. Это свойство называется масштабной инвариантностью.

Гауссов клубок характеризуется единственным макроскопическим пространственным масштабом. Это означает, что все характеристики его макроскопических размеров, т. е. радиус инерции, гидродинамический радиус, расстояние между концами цепи совпадает по порядку величины, все они порядка радиуса корреляции. С единственностью масштаба связано свойство масштабной инвариантности гауссова клубка.

Гауссов клубок является очень рыхлым и относится к сильно флуктуирующим системам. К таким системам относится раствор полимера в хорошем растворителе при малой концентрации. Сильно флуктуирующие системы, в том числе раствор полимера, характеризуется критическими показателями, которые универсальны, т. е. не зависят от конкретного химического строения макромолекул и определяются лишь самыми общими их свойствами – цепным строением, разветвленностью и т. д.

Масштабная инвариантность, т. е. единственность характерного размера, требует единственности характерной концентрации полимерного раствора. По мере концентрирования полимерный раствор проходит через три качественно различных состояния: разбавленный, где отдельные клубки не перекрываются; полуразбавленный, где клубки сильно перекрываются, но объемная доля полимера в растворе мала; концентрированный, где объемная доля полимера порядка единицы.

Объемная доля полимера в растворе , равна произведению концентрации звеньев на собственный объем звена :

Между разбавленными и полуразбавленными растворами лежит граничная концентрация , по порядку величины совпадающая с концентрацией звеньев внутри отдельной макромолекулы.