3.10. Кинетика адсорбции
Кинетика адсорбции
подчиняется уравнению первого порядка.
Чем больше насыщение поверхности, т. е.
меньше разность (
),
тем меньше скорость адсорбции.
С повышением температуры скорость адсорбции увеличивается, а равновесная адсорбция уменьшается (рис. 3.13).
Рис. 3. 13. Кинетика адсорбции.
Константа зависит от теплоты адсорбции, температуры и коэффициента диффузии адсорбата. Температурный коэффициент адсорбции мал, т. к. энергия активации физической адсорбции равна 0.
3.11. Классическая теория адсорбции
Ленгмюр и Поляни одновременно в 1915 году разработали теории адсорбции. Эти теории являются ограниченными. Они применяются в зависимости от природы адсорбента и адсорбата и условий адсорбции. Теория Ленгмюра рассматривает физическую и химическую адсорбцию при малом давлении и температуре ниже критической. Она неприменима к тонкопористым сорбентам. Теория Поляни применима только к физической адсорбции.
3.11.1. Теория мономолекулярной адсорбции Ленгмюра
Теория Ленгмюра учитывает ограниченность поверхности адсорбента, что приводит к адсорбционному насыщению поверхности по мере увеличения концентрации адсорбата.
При разработке этой теории Ленгмюром были сделаны следующие допущения:
Адсорбция локализована, адсорбционные силы близки к химическим.
Адсорбция происходит на активных центрах адсорбента, которые энергетически эквивалентны.
Радиус действия адсорбционных сил мал, и один активный центр адсорбирует одну молекулу адсорбата, причем образуется мономолекулярный адсорбционный слой.
Устанавливается динамическое равновесие адсорбция десорбция.
Между адсорбированными молекулами отсутствует взаимодействие, вследствие чего время пребывания на поверхности не зависит от того, занят соседний активный центр или нет.
Вывод уравнения Ленгмюра.
Ленгмюр рассматривал адсорбцию как квазихимическую реакцию между газом и активными центрами с образованием адсорбционного комплекса.
Обозначим давление
газа через
,
концентрацию свободных активных центров
через
,
концентрацию занятых активных центров
через
.
Тогда константа равновесия
.
;
;
;
;
Очевидно, величина равна поверхностной концентрации адсорбата, т. е. количеству адсорбированного вещества а, т.к. один активный центр занимает одна молекула адсорбата.
;
Иногда числитель и знаменатель этого
выражения делят на
.
.
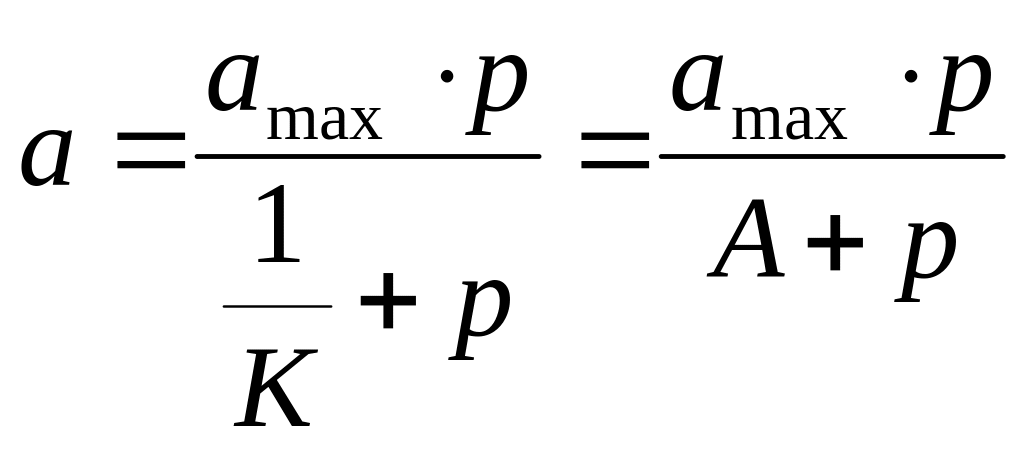Константы уравнения
Ленгмюра имеют следующий смысл.
- это максимальная адсорбция при
образовании мономолекулярного слоя,
т. е. емкость монослоя.
- константа адсорбционного равновесия,
связанная с теплотой адсорбции. К
характеризует энергию взаимодействия
адсорбата с адсорбентом, т. е. химическое
сродство. Для любой химической реакции
справедливо выражение
;
;
;
Анализ уравнения Ленгмюра
Рассмотрим насколько хорошо описывает уравнение Ленгмюра изотерму адсорбции на всех ее участках.
На изотерме адсорбции,
изображенной на рис. 3.10 можно выделить
три участка. При малых значениях
всегда можно подобрать такое значение
,
когда значение
,
и уравнение Ленгмюра принимает вид:
,
То есть
пропорциональна
,
что соответствует начальному линейному
участку кривой. При больших значениях
можно подобрать такие значения
,
когда величина
и
,
что соответствует третьему участку
изотермы. Второй криволинейный участок
изотермы описывается полным уравнением
Ленгмюра. Таким образом, это уравнение
хорошо описывает всю изотерму адсорбции,
в отличие от уравнения Фрейндлиха.
Существует два способа графического решения уравнения Ленгмюра (рис 3.14).
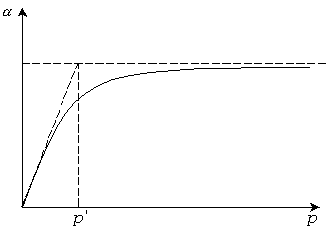
Рис. 3.14. Решение уравнения Ленгмюра.
По первому способу по
изотерме находят значение
.
Затем продолжают начальный прямолинейный
участок изотермы до пересечения с линией
и из точки пересечения опускают
перпендикуляр до точки
на оси абсцисс. При малых
значение
,
и им знаменателе можно пренебречь. Тогда
уравнение принимает вид:
.
При
.
Отсюда
.
Второй способ решения уравнения Ленгмюра применяется, когда экспериментальная изотерма не имеет третьего линейного участка, т. е. значение неизвестно. Уравнение преобразуется в уравнение прямой:
;
;
Рис.3.15.
Решение уравнения Ленгмюра
;
Уравнение Ленгмюра позволяет определить удельную поверхность адсорбента.
Действительно,
произведение
равно числу
молекул, приходящихся на 1 см2
поверхности. Умножив это значение на
площадь, занимаемую одной молекулой
получим величину удельной поверхности
.
Рис. 3.16. Изотерма полимолекулярной адсорбции.
Часто изотермы адсорбции имеют вид, отличающийся от ленгмюровской изотермы, а именно -образный вид (Рис. 3.16). Это объясняется полимолекулярной адсорбцией, или капиллярной конденсацией. Изотермы адсорбции полимеров, как правило, не являются ленгмюровскими, т. к. одна макромолекула занимает несколько активных центров адсорбента, т. е. предпосылки, положенные в основу уравнения Ленгмюра, не соблюдаются.