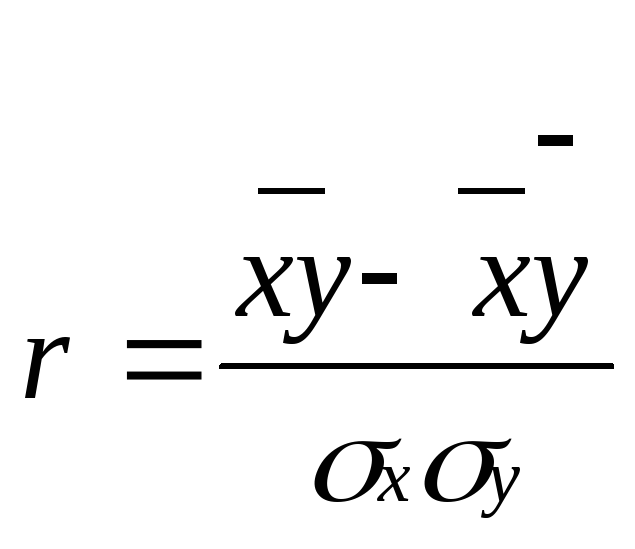Контрольні завдання

Тестові завдання зазначені після даної теми методичних рекомендацій до самостійної роботи.

Ситуаційна вправа

Задача 1. Підприємство для виробництва трьох видів продукції має три види матеріальних ресурсів: виду А – 1000 кг, виду В – 500 кг, виду С – 600 кг (див.табл.3.1)

Таблиця 3.1

Витрати матеріальних ресурсів

Вид матеріальних ресурсів	Витрати матеріальних ресурсів на один вироб типу “Д”, кг	Витрати матеріальних ресурсів на один вироб типу “Л”, кг	Витрати матеріальних ресурсів на один вироб типу “М”, кг	Всього матеріалів по видам ресурсів, кг
А	2,0	0,0	4,0	1000
В	1,0	5,0	0,0	500
С	2,0	2,0	1,0	600
Прибуток від реалізації одного виробу, тис.грн..	4,0	5,0	6,0	-

Враховуючи обмежену кількість матеріальних ресурсів, розрахуйте при якому обсязі виробництва підприємство матиме максимальний прибуток і яке буде його значення.

Бібліографічний список:

6,12,13,17,19,21,27

Практичне заняття № 2

Тема 2: Зміст финансового планування і прогнозування.

План заняття

1. Методи фінансового планування.

2. Економетричні моделі і прогнози як інструменти планування.

3. Основні етапи складання фінансового плану.

Навчальні цілі

Цілями проведення практичного заняття є: Закріпити теоретичні знання і сформувати практичні навики з використання кореляційно-регресійного аналізу у фінансовому плануванні

Обладнання, яке потрібне для проведення практичного заняття

1. Методичні рекомендації.

2.Контрольні завдання.

3.Мікрокалькулятори.

Методичні рекомендації до практичного заняття

Методи фінансового планування - це конкретні прийоми й способи техніко-економічних розрахунків і обґрунтування планових завдань та їх ув'язування.

У процесі фінансового планування найчастіше використовуються такі методи планування, як нормативний, розрахунково-аналітичний, балансовий, оптимізації планових завдань, економіко-математичне моделювання, експертних оцінок, коефіцієнтів і програмно-цільовий.

Нормативний метод ґрунтується на використанні науково обґрунтованих норм і нормативів, цін, тарифів, ставок, розцінок, затверджених відповідно до чинного законодавства, для техніко-економічного обґрунтування планових завдань.

Нормативний метод застосовується:

• при плануванні витрат (норми витрачання сировини, матеріалів, палива, теплової і електричної енергії на одиницю продукції, ставки розцінки з оплати праці, відсоткові ставки відрахувань у державні цільові фонди, норми амортизаційних відрахувань тощо);

• при плануванні валового і чистого прибутку (розрахункові норми надбавок (націнок) і рентабельності, ставки податків і зборів тощо);

• при нормуванні запасів оборотних засобів (норми запасів сировини, матеріалів, палива, готової продукції, товарів в днях обороту);

• при прогнозуванні використання чистого прибутку (відсотки відрахувань на виплату дивідендів, поповнення статутного і резервного капіталу, на реальні інвестиції, на цільове спрямування соціального призначення тощо);

• при розрахунку інших показників фінансового плану.

Розрахунково-аналітичний метод передбачає використання даних економічного аналізу, коли на підставі фактично досягнутих показників, прийнятих за базу, і прогнозованого індексу їх зміни визначаються планові завдання. Цей метод застосовується за відсутності техніко-економічних норм і нормативів. Він базується на глибокому всебічному аналізі й оцінці звітних даних за останні два-три роки, експертній оцінці досягнутого і визначенні перспектив подальшого розвитку.

В умовах економічної нестабільності розрахунково-аналітичний метод широко застосовується при плануванні окремих статей витрат, валового прибутку, розрахункового рівня рентабельності, нормативу оборотних коштів та багатьох інших показників фінансового плану.

Метод оптимізації планових завдань — це метод багатоваріантних розрахунків, що передбачає вибір кращої з них. Критерії вибору можуть бути різними, залежно від поставленої мети. Ними можуть бути: мінімум затрат; максимум доходу і прибутку на вкладені ресурси; мінімум приведених затрат; мінімум часу на оборот капіталу; оптимальна величина оборотних коштів тощо.

Метод оптимізації планових завдань застосовується при економічному обґрунтуванні планових витрат, прогнозуванні фінансових можливостей господарюючого суб'єкта, прогнозуванні структури розміщення власного капіталу тощо.

Балансовий метод є одним із основних методів фінансового планування. З його допомогою ув'язуються поточні витрати з валовим прибутком та прогнозується беззбиткова робота структурних підрозділів і організації та підприємства в цілому. З допомогою балансового методу досягається ув'язування прогнозованих видатків з наявними фінансовими ресурсами та прогнозованим їх приростом і забезпечується ресурсне збалансування плану економічного і соціального розвитку (бізнес-плану) з основних напрямів діяльності. Зведений фінансовий план складається у формі балансу доходів і видатків.

Балансовим методом складається прогнозний баланс активів і пасивів підприємства, баланс грошових потоків тощо.

Метод експертних оцінок — це метод перевірки ймовірності виконання планових завдань під впливом обчислення можливих типів ризику, з якими може зіткнутися господарюючий суб'єкт. Експертна оцінка доповнює економіко-математичне моделювання і проводиться з метою визначення ступеня ризику під впливом тих чи інших причин, пошуку шляхів запобігання ризику, розробки альтернативних програм тощо. Після експертних оцінок можливе коригування розроблених планових завдань і прогнозів.

Метод коефіцієнтів - це метод, з допомогою якого оцінюється склад, структура, раціональність розміщення та ефективність використання капіталу, вкладеного в активи підприємства, проводиться експрес-аналіз і оцінка фінансового стану підприємства. Комплексний аналіз коефіцієнтів дає можливість розробити нормативні еталонні показники щодо забезпечення фінансової стійкості та отримання прогнозованого економічного ефекту на вкладений капітал.

Програмно-цільовий метод - це метод, який передбачає розробку фінансового плану, виходячи з мети і завдань, передбачених планом (програмою) економічного і соціального розвитку підприємства. Розробка цільових програм і завдань підпорядковується основній меті - ресурсному збалансуванні потреби підприємства в капіталі для забезпечення виконання прогнозованих бізнес-планом обсягів операційної, інвестиційної та інших видів діяльності та отриманню прибутку, достатнього для нарахування прогнозованих дивідендів власникам капіталу та забезпечення економічного і соціального розвитку підприємства в поточному і наступному періодах.

Економіко-математичне моделювання — це метод, з допомогою якого вивчаються взаємозв'язки між економічними процесами, визначається вплив тих чи інших чинників, встановлюється закономірність зміни економічних явищ під впливом низки чинників.

Економіко-математичні моделі можна будувати за функціональним або кореляційним зв'язками.

У процесі фінансового аналізу і планування на рівні господарюючого суб'єкта найчастіше застосовують моделі функціонального зв'язку. Функціональний зв'язок можна алгебраїчно відобразити функцією (формулою), що встановлює повну відповідність між факторною і результативною ознаками.

Кореляційний зв'язок виявляється при великій кількості виборок і лише через середні величини. Тому моделі кореляційного зв'язку можуть застосовуватися лише в процесі фінансового аналізу і прогнозування за наявності даних значної кількості однорідних підприємств.

Економіко-математичне моделювання нерідко застосовується при аналізі ефективності використання матеріальних, трудових і фінансових ресурсів, дає можливість з певною ймовірністю визначити динаміку показників залежно від зміни чинників, що впливають на розвиток фінансових процесів у майбутньому. Результати скономіко-математичного моделювання кладуться в основу техніко-економічних розрахунків планових завдань і прогнозів.

В основі будь–якого наукового дослідження лежить вивчення зв’язків між явищами. Закони, що відкриваються наукою, являють собою вираз цих зв`язків, об`єктивних, внутрішніх зв`язків світу. Жодне явище, чи то в суспільстві, чи то в природі, не може бути вивченим поза зв’язку з іншими явищами.

Характерною особливістю кореляційної форми зв’язку є його прояв у змінах таких узагальнюючих статистичних характеристиках як середні величини. Цим кореляційні зв’язки відрізняються від стохастичних (ймовірнисних). При стохастичних зв’язках середні можуть залишатися сталими, якщо навіть розподіл окремих значень ознаки змінюються.

Подаючи ймовірнісний зв`язок між явищами, кореляція передбачає, що розподіл обох корельованих ознак повинен носити ознаки випадковості.

Вивчення кореляційних зв`язків передбачає рішення задачі визначення тісноти цих зв`язків, а також їх форми.

Під формою кореляційного зв`язку розуміють ту тенденцію, яка проявляється в змінах ознаки, що вивчається, у зв`язку із змінами ознаки-фактора. Якщо спостерігається тенденція рівномірного зростання або спадання значень ознаки, то зв`язок називається прямолінійним. При тенденції нерівномірних змін цих значень зв`язок носить назву - криволінійний.

Лінія на графіку, що відображає тенденцію зміни ознаки, яка корелює з ознакою фактором, називається лінією регресії. Така лінія і є графічним виразом форми зв’язку.

Лінія регресії показує такі зміни середніх значень однієї із випадкових змінних, які б відбулися із зміною значень іншої, при умові ізольованості від стороннього впливу.

Очевидним є те, що лінія регресії повинна проходити максимально близько до ламаної лінії, яка представляє дані, одержані в результаті статистичного спостереження. Математично ця задача вирішується за допомогою багатьох способів, найпоширенішим з яких є – метод найменших квадратів (МНК).

Даний метод встановлює конкретні правила, які дозволяють із множини різних оцінок одним шляхом вибрати систему параметрів. При застосуванні МНК висувається вимога, щоб сума квадратів різниць між значеннями ознаки “по лінії регресії” і її емпіричними значеннями була мінімальною.

За напрямом зв’язок між корелюючими величинами може бути прямим і оберненим. При прямому зв’язку із збільшенням факторної ознаки збільшується і результативна. Якщо ж із збільшенням факторної ознаки спостерігається зменшення результативної ознаки такий зв’язок називається оберненим.

Прямолінійну регресію виражають рівнянням прямої лінії

y = b₀ + b₁x, (10)

де у – теоретичне значення ознаки; b₀ і b₁ – параметри рівняння; х – значення фактора.

З

{

находження параметрівb₀ і b₁ за методом найменших квадратів зводиться до рішення системи рівнянь, які носять назву нормальних:

y = b₀*n + b₁x; (11)

yx = b₀x + b₁x²;

Після визначення невідомих параметрів регресійної моделі оцінюють щільність зв’язку між залежною величиною у і незалежною х.

Одним із критеріїв, який кількісно оцінює цей вплив є коефіцієнт кореляції:

(12)

Він може бути розрахованим і за іншими формулами:

Коефіцієнт кореляції знаходиться в межах від 0 до 1. Якщо його значення додатнє, то це свідчить про прямий зв’язок між показниками, якщо від’ємне – зворотній. Знак коефіцієнта кореляції завжди збігається із знаком коефіцієнта регресії.

Якщо r < 0,3  – зв’язку не існує;

0,3  r < 0,5 - зв’язок слабкий;

0,5  r < 0,7 - зв’язок середній;

r  0,7 - зв’язок високий.

Повну характеристику лінійного зв’язку можна одержати, користуючись критерієм лінійної кореляційної залежності.

Піднесений до квадрата коефіцієнт кореляції називають коефіцієнтом детермінації (R). Він показує, яка частка загальної варіації ознаки обумовлена фактором, що вивчається. Його часто виражають у процентах. Величина R завжди знаходиться у проміжку від 0 до +1.

При криволінійному кореляційному зв’язку однаковим змінам середніх значень факторної ознаки відповідають різні зміни середніх значень результативної ознаки. Криволінійний зв’язок визначають за рівнянням кривої лінії.

В статистичному аналізі при нелінійній формі зв’язку найчастіше використовують параболічну і гіперболічну форми кривої.

Якщо криволінійна залежність має форму параболи другого порядку, то зв’язок виражають рівнянням:

y_x = b₀ + b₁ + b₂x² (13)

Параметри b₀ ,b₁, b₂ визначають складанням і рішенням системи із трьох рівнянь:

y =nb₀ + b₁ x+ b₂x²

yx= b₀ x+ b₁ x²+ b₂x³

yx²= b₀ x²+ b₁ x³+ b₂x⁴

Коли залежність між корелюючими величинами має гіперболічний характер її встановлюють за рівнянням гіперболи:

y_x = b₀ + b₁/x (14)

При цьому для розрахунку параметрів b₀ і b₁ застосовують систему рівнянь:

y =nb₀ + b₁ 1/x

y/x= b₀ 1/x+ b₁ 1/x²

В залежності від кількості факторних ознак кореляцію поділяють на просту (парну) і множинну. При парній кореляції аналізують зв’язок між факторною і результативною ознаками. На практиці економічні процеси змінюється під впливом багатьох факторів. Тому для їх аналізу застосовують частіше множинну кореляцію, яка характеризується наявністю двох і більше факторних ознак.

Узагальнена багатофакторна лінійна регресійна модель має вигляд:

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ +...+ b_nx_n (15)

Таким чином дана багатофакторна лінійна модель має n незалежних змінних, або факторів, які впливають на залежну змінну у.

Складність узагальнення інформації та розрахунків призводять до необхідності застосування обчислювальної техніки. Побудова та аналіз багатофакторних моделей базується на використанні відповідних програмних продуктів (BMDP Statistical Software, SAS, SPSS, RATS, STATGRAPHICS, STATISTICA та ін.).

Використання системи STATІSTICA

STATІSTICA є інтегрованою системою статистичного аналізу і обробки даних. Вона складається із слідуючи основних компонентів:

• електронні таблиці для введення даних, а також спеціальних таблиць для виведення результатів аналізу;

• графічна система для візуалізації даних і результатів статистичного аналізу;

• статистичні модулі, в яких зібрані групи статистичних процедур;

• інструментарій для підготовки звітів;

• вбудована мова програмування.

STATІSTICA включає в себе слідуючи спеціальні статистичні модулі: Основні статистики і таблиці, Непараметрична статистика, Дисперсійний аналіз, Множинна регресія, Факторний аналіз, Аналіз часових рядів і прогнозування та ін.

Модуль Множинна регресія включає в себе вичерпний набір засобів множинної лінійної та фіксованої нелінійної регресії, включаючи покрокові методи, ридж–регресію та ін. Система дозволяє розрахувати всебічний набір статистик і розширеної діагностики, включаючи повну регресійну таблицю, кореляції і коваріації, матриці прогонки, статистику Турбіна–Ватсона і т.д. Допускається до 300 змінних в процедурі регресії.

Данні в STATІSTICA організовані у вигляді електронної таблиці – Spreadeheet. Вони можуть містити як числову так і текстову інформацію. Система дає можливість автоматичного створення відповідних звітів.

Статистичний обробіток даних в системі STATІSTICA складається із слідуючи основних кроків:

• введення даних в електронну таблицю системи;

• попереднє перетворення даних перед безпосереднім застосуванням конкретного статистичного методу;

• візуалізація даних за допомогою того чи іншого типу графіків;

• статистичний аналіз за допомогою конкретного статистичного методу. Підбір моделі і задання необхідних параметрів в статистичних процедурах;

• виведення числових, текстових і графічних результатів, як на екран так і в файл із звітом;

• аналіз результатів.

Після запуску програми на екрані з’являється Перемикач модулів (Module Switcher), за допомогою якого можна вибрати необхідний для роботи модуль. Для проведення кореляційно–регресійного аналізу в меню вибирають – Multiple Regression (Множинна регресія). В результаті на екрані відкривається головне вікно системи STATІSTICA. Якщо запускається STATІSTICA в перше, то при цьому відкривається файл з вихідними даними, який називається Adstudy.sta. Разом з цим на моніторі з’являється Стартова панель модуля, яка містить основні операції і яка дозволяє визначити основні параметри налізу.

Вибираючи потрібні пункти Стартової панелі можна відкрити необхідний файл даних для аналізу, вибрати необхідні підмножини випадків і змінні для аналізу.

Змінні в електронній таблиці системи можуть приймати як текстові, так і числові значення. Крім цього таблиця може включати і додаткову інформацію.

Для використання графічних можливостей пакета STATІSTICA існує меню Graphics (Графіка). В діалоговому вікні Variables (Змінні) вибирають змінні, які необхідно відобразити графічно, а також відповідний тип графіка.

Починають статистичний аналіз із виклику Стартової панелі модуля і вибору залежної і незалежних змінних (кнопка Variables) у вікні Select dependet and independet variable list (Вибір залежної змінної і списку незалежних змінних). Натиснувши ОК дослідник потрапляє знову в Стартову панель модуля Множинна регресія.

Після натиснення ОК на Стартовій панелі починається процес обчислення і виведення результатів на екран. При цьому, результати аналізу мають таку структуру: верхня частина вікна – інформаційна, нижня – містить функціональні кнопки, які дозволяють всебічно переглянути результати аналізу.

В модулі Множинна регресія в STATІSTICA залишки досліджуються в спеціальному вікні Аналіз залишків. Досліджуючи залишки можна оцінити ступінь адекватності моделі. Для цього необхідно натиснути у вікні Результати множинної регресії кнопку Residual analysis (Аналіз залишків). За допомогою функціональних кнопок у новому вікні можна всебічно переглянути залишки моделі як у графічному вигляді, так і в електронних таблицях.