
- •Общая информация
- •Методические указания
- •Комплект поставки, требования к системе, процедура запуска
- •Принцип построения и структура
- •Знакомство с ЭУМК
- •Рекомендации для преподавателя
- •Лекции
- •Организация практических занятий
- •Тесты
- •Рекомендации для студента
- •Изучение теоретического материала
- •Практические занятия
- •Тесты
- •Типовые программы курсов
- •Указатель по направлениям и специальностям
- •Список учебных программ
- •Рекомендуемая литература
- •Часть I. Теория
- •Глава 1. Аналитическая геометрия
- •1.1. Прямая на плоскости
- •1.1.1. Декартовы координаты
- •1.1.2. Уравнение прямой с угловым коэффициентом
- •1.1.3. Уравнение прямой по точке и угловому коэффициенту
- •1.1.4. Уравнение прямой, проходящей через две данные точки
- •1.1.5. Общее уравнение прямой
- •1.1.7. Угол между двумя прямыми
- •1.1.8. Условия параллельности и перпендикулярности двух прямых
- •1.1.9. Расстояние от точки до прямой
- •1.1.10. Взаимное расположение двух прямых на плоскости
- •1.2. Кривые второго порядка
- •1.2.1. Окружность
- •1.2.2. Эллипс
- •1.2.3. Гипербола
- •1.2.4. Парабола
- •1.2.5. Кривые второго порядка со смещенным центром
- •Глава 2. Предел последовательности и функции
- •2.1. Предел числовой последовательности
- •2.1.1. Числовая последовательность
- •2.1.2. Предел последовательности
- •2.1.3. Бесконечно малые последовательности
- •2.1.4. Бесконечно большие последовательности
- •2.1.5. Сходящиеся последовательности
- •2.1.6. Предельный переход в неравенствах
- •2.1.7. Монотонные последовательности
- •2.1.8. Непрерывное начисление процентов
- •2.2. Функциональная зависимость
- •2.2.1. Понятие функции
- •2.2.2. Способы задания функции.
- •2.2.3. Основные характеристики функций
- •2.2.4. Понятие обратной и сложной функции
- •2.2.5. Элементарные функции
- •2.2.6. Построение графиков функций
- •2.2.7. Функциональная зависимость в экономике
- •2.3. Предел функции. Два замечательных предела
- •2.3.1. Предел функции по Гейне
- •2.3.2. Предел функции по Коши
- •2.3.3. Односторонние пределы
- •2.3.4. Бесконечно малые функции
- •2.3.5. Бесконечно большие функции
- •2.3.6. Свойства предела функции
- •2.3.7. Признак существования предела функции
- •2.3.8. Замечательные пределы
- •2.3.9. Эквивалентные бесконечно малые функции
- •2.4. Непрерывные функции
- •2.4.1. Непрерывность функции в точке
- •2.4.2. Теоремы о непрерывных в точке функциях
- •2.4.3. Точки разрыва и их классификация
- •2.4.4. Непрерывность элементарных функций
- •2.4.5. Теоремы о непрерывных на отрезке функциях
- •Глава 3. Теория дифференцирования
- •3.1. Производная. Вывод таблицы
- •3.1.1. Понятие производной
- •3.1.2. Геометрический смысл производной
- •3.1.3. Физический смысл производной
- •3.1.4. Правила дифференцирования
- •3.1.5. Таблица производных основных элементарных функций. Производная сложной и обратной функции
- •3.1.6. Логарифмическая производная
- •3.1.7. Производная неявной функции
- •3.1.8. Производные высших порядков
- •3.1.9. Применения производной в экономике
- •3.2.1. Понятие дифференцируемости функции в точке
- •3.2.2. Дифференциал функции и приближенные вычисления с помощью дифференциала
- •3.2.3. Геометрический смысл дифференциала
- •3.2.4. Теоремы о среднем
- •3.3. Правила Лопиталя. Формула Тейлора
- •3.3.1. Правила Лопиталя
- •3.3.2. Формула Тейлора
- •3.4. Исследование функции с помощью производной
- •3.4.1. Условие постоянства функции.
- •3.4.2. Достаточное условие монотонности функции.
- •3.4.3. Необходимые и достаточные условия локального экстремума
- •3.4.4. Наибольшее и наименьшее значения функции
- •3.4.5. Выпуклые функции
- •3.4.6. Асимптоты графика функции
- •3.4.7. Общая схема исследования поведения функций и построения графиков функций
- •Глава 4. Теория интегрирования
- •4.1. Неопределенный интеграл
- •4.1.1. Первообразная
- •4.1.2. Неопределенный интеграл
- •4.1.3. Таблица интегралов
- •4.1.4. Простейшие методы интегрирования
- •Метод интегрирования подстановкой (замена переменной)
- •Метод интегрирования по частям
- •Интегрирование простейших рациональных дробей
- •4.2. Интегрирование классов функций
- •4.2.1. Интегрирование рациональных функций
- •4.2.2. Интегрирование иррациональных функций
- •Простейшие случаи
- •Более сложные случаи
- •4.2.3. Тригонометрические интегралы
- •4.3. Определенный интеграл
- •4.3.1. Задача о вычислении площади криволинейной трапеции
- •4.3.2. Свойства определенного интеграла
- •4.3.3. Оценки интегралов. Теорема о среднем значении.
- •4.3.4. Необходимое условие интегрируемости функции
- •4.3.5. Достаточные условия интегрируемости
- •4.3.6. Интеграл с переменным верхним пределом. Существование первообразной для непрерывной функции.
- •4.3.8. Замена переменной и интегрирование по частям в определенном интеграле.
- •4.4.1. Площадь криволинейной трапеции.
- •4.4.2. Длина дуги кривой
- •4.4.3. Объем тела вращения
- •4.4.4. Использование понятия определенного интеграла в экономике
- •4.5. Несобственные интегралы.
- •4.5.1. Несобственный интеграл с бесконечными пределами интегрирования.
- •4.5.2. Несобственные интегралы от неограниченных функций.
- •Глава 5. Дифференцирование функций двух переменных
- •5.1. Функция двух переменных. Дифференциал
- •5.1.1. Определения
- •5.1.2. Предел функции двух переменных
- •5.1.3. Непрерывность функции двух переменных
- •5.1.4. Частные производные
- •Геометрический смысл частных производных
- •5.1.5. Частные производные высших порядков
- •5.1.6. Дифференцируемость и дифференциал
- •5.1.7. Производная сложной функции
- •5.1.8. Производная по направлению. Градиент
- •5.1.9. Производственная функция Кобба — Дугласа
- •5.2. Экстремум функции двух переменных
- •5.2.1. Локальный экстремум
- •5.2.2. Глобальный экстремум
- •5.2.3. Условный экстремум
- •5.2.4. Метод множителей Лагранжа
- •5.2.5. Экстремум выпуклых функций
- •5.2.6. Функция полезности
- •Глава 6. Дифференциальные уравнения
- •6.1.1. Общее дифференциальное уравнение (ДУ) первого порядка.
- •6.1.2. Составление дифференциальных уравнений.
- •6.1.3. ДУ с разделяющимися переменными.
- •6.2. Дифференциальные уравнения первого порядка и их решение
- •6.2.1. Однородные ДУ первого порядка.
- •6.2.2. Линейные дифференциальные уравнения первого порядка.
- •6.2.3. Уравнение Бернулли.
- •Глава 7. Ряды
- •7.1. Числовые ряды
- •7.1.1. Понятие числового ряда.
- •7.1.2. Необходимое условие сходимости числового ряда.
- •7.1.3. Достаточные условия сходимости.
- •7.1.4. Абсолютная и условная сходимость.
- •7.2. Функциональные ряды. Область сходимости
- •7.3. Степенные ряды. Формула Тейлора
- •Глава 8. Линейная алгебра
- •8.1. Матрицы и определители
- •8.1.1. Понятие матрицы. Виды матриц
- •8.1.2. Операции над матрицами
- •8.1.3. Определители
- •8.1.4. Свойства определителей
- •8.1.5. Элементарные преобразования
- •8.1.6. Обратная матрица
- •8.1.7. Матричные уравнения
- •8.1.8. Ранг матрицы
- •8.2. Системы линейных алгебраических уравнений
- •8.2.1. Основные понятия
- •8.2.2. Матричный метод
- •8.2.3. Метод Крамера
- •8.2.4. Метод Гаусса
- •8.2.5. Критерий Кронекера — Капелли
- •8.2.6. Экономическая модель Леонтьева
- •8.3. Векторная алгебра
- •8.3.1. Векторы в пространстве
- •8.3.2. Скалярное произведение векторов
- •8.3.4. Линейная зависимость векторов
- •8.3.5. Базис и ранг системы векторов
- •8.3.6. Ортогональные системы векторов
- •8.3.7. Фундаментальные системы решений
- •8.3.8. Собственные векторы и значения
- •Предметный указатель
- •Другие
- •Определения
- •Абсолютно сходящийся ряд
- •Абсолютно сходящийся функциональный ряд
- •Алгебраическое дополнение
- •Арифметические операции с последовательностями
- •Асимптоты гиперболы
- •Базисный минор
- •Бесконечно большая последовательность
- •Бесконечно большие функции
- •Бесконечно малая последовательность
- •Бесконечно малые функции
- •Бюджетное множество
- •Вектор валового выпуска
- •Вектор конечного продукта
- •Вектор предельных полезностей
- •Вектор-столбец и вектор-строка
- •Вертикальная асимптота
- •Вершина параболы
- •Вершины гиперболы
- •Вершины эллипса
- •Возрастающая и убывающая последовательности
- •Возрастающая и убывающая функции
- •Второй замечательный предел
- •Выпуклая вверх (выпуклая) функция
- •Выпуклая вниз (вогнутая) функция
- •Выпуклое множество
- •Выпуклые функции
- •Гаусса метод
- •Гипербола
- •Градиент
- •График функции двух переменных
- •График функции
- •Диагонали матрицы
- •Диагональная матрица
- •Директриса параболы
- •Дифференциал функции двух переменных
- •Дифференциал
- •Дифференциальное уравнение Бернулли
- •Дифференциальное уравнение первого порядка
- •Дифференциальное уравнение с разделенными переменными
- •Дифференциальное уравнение с разделяющимися переменными
- •Дифференциальный бином
- •Дифференцирование
- •Дифференцируемая функция
- •Дифференцируемость функции двух переменных
- •Единичная матрица
- •Задача Коши
- •Знакочередующийся ряд
- •Изокванты
- •Интеграл с переменным верхним пределом
- •Интегральная кривая дифференциального уравнения
- •Интегральная кривая
- •Интегральная сумма
- •Интегрирование дифференциального уравнения
- •Интервал монотонности
- •Интервал сходимости
- •Касательная
- •Квадратная матрица
- •Классификация точек разрыва
- •Крамера метод и формулы
- •Кривые безразличия
- •Критическая точка
- •Левый предел
- •Линейное дифференциальное уравнение
- •Линии первого порядка
- •Линии уровня
- •Линия на плоскости
- •Логарифмическая производная
- •Локальные минимум и максимум функции двух переменных
- •Локальный максимум
- •Локальный минимум
- •Локальный экстремум функции двух переменных
- •Локальный экстремум
- •Матрица прямых затрат
- •Матрицы
- •Матричная форма системы линейных уравнений
- •Матричные уравнения
- •Матричный метод решения системы линейных уравнений
- •Минор матрицы
- •Минор элемента матрицы
- •Многочлен Тейлора
- •Многочлен от квадратной матрицы
- •Монотонная последовательность
- •Монотонная функция
- •Наклонная асимптота
- •Направление
- •Направляющие косинусы
- •Невырожденная и вырожденные матрицы
- •Неограниченная последовательность
- •Неограниченная функция
- •Неопределенный интеграл
- •Неправильная рациональная функция
- •Непрерывная в области функция
- •Непрерывная на отрезке функция
- •Непрерывность функции двух переменных по одной из переменных
- •Непрерывность функции двух переменных
- •Непрерывность функции на языке приращений
- •Непрерывность функции
- •Непрерывность функций двух переменных на языке приращений
- •Непрерывные справа и слева функции
- •Несобственный интеграл второго рода
- •Несобственный интеграл первого рода
- •Неэлементарные функции
- •Неявная функция
- •Нормаль
- •Нулевая матрица
- •Нулевое решение однородной системы линейных уравнений
- •Область сходимости
- •Обратная матрица
- •Обратная функция
- •Общее решение дифференциального уравнения
- •Общее уравнение прямой
- •Общий интеграл
- •Ограниченная последовательность
- •Ограниченная функция
- •Одноресурсная производственная функция
- •Однородная функция
- •Однородное дифференциальное уравнение
- •Однородные и неоднородные системы линейных уравнений
- •Однородные функции
- •Односторонние пределы на бесконечности
- •Односторонние пределы
- •Окрестность точки на плоскости
- •Окрестность точки
- •Окружность
- •Определённая и неопределённая системы
- •Определенный интеграл
- •Определители второго порядка
- •Определители первого порядка
- •Определители третьего порядка
- •Определитель произвольного порядка
- •Оси гиперболы
- •Оси эллипса
- •Основная матрица системы
- •Основной прямоугольник гиперболы
- •Особое решение дифференциального уравнения
- •Остаток числового ряда
- •Остаточный член в форме Лагранжа
- •Ось параболы
- •Парабола
- •Параметр параболы
- •Первообразная
- •Первый замечательный предел
- •Перестановочные матрицы
- •Периодическая функция
- •Полное приращение функции
- •Полуоси гиперболы
- •Полуоси эллипса
- •Последовательность числовая
- •Постоянная последовательность
- •Постоянная функция
- •Правильная рациональная функция
- •Правый предел
- •Предел последовательности
- •Предел функции двух переменных на языке окрестностей
- •Предел функции двух переменных по Гейне
- •Предел функции двух переменных по Коши
- •Предел функции на бесконечности
- •Предел функции на языке окрестностей
- •Предел функции по Гейне
- •Предел функции по Коши
- •Предельная производительность труда
- •Предельная фондоотдача
- •Предельные полезности
- •Приращение аргумента и функции
- •Приращение функции по направлению
- •Присоединённая матрица
- •Произведение матриц
- •Произведение матрицы на число
- •Производная второго порядка
- •Производная по направлению
- •Производная
- •Производственная функция Кобба — Дугласа
- •Производственная функция
- •Простейшие рациональные дроби
- •Противоположная матрица
- •Равенство матриц
- •Равнобочная гипербола
- •Равномерно сходящийся функциональный ряд
- •Радиус сходимости
- •Разность матриц
- •Ранг матрицы
- •Расширенная матрица системы
- •Рациональные функции
- •Решение дифференциального уравнения
- •Решение системы уравнений
- •Ряд матрицы
- •Система линейных уравнений
- •Сложная функция
- •Смешанные производные
- •Совместные и несовместные системы уравнений
- •Согласованные матрицы
- •Соотношения баланса
- •Сопряженные гиперболы
- •Стационарная точка
- •Стационарные точки функции двух переменных
- •Степенной ряд
- •Степень квадратной матрицы
- •Строго возрастающая и строго убывающая последовательности
- •Строго возрастающие и строго убывающие функции
- •Строго монотонная последовательность
- •Строго монотонная функция
- •Ступенчатая матрица
- •Сумма матриц
- •Сходимость в точке
- •Сходящаяся и расходящаяся последовательности
- •Сходящийся несобственный интеграл
- •Сходящийся числовой ряд
- •Таблица эквивалентностей
- •Точка безубыточности
- •Точка перегиба
- •Точка разрыва функции двух переменных
- •Точка рыночного равновесия
- •Точка спроса
- •Точки локального условного максимума и минимума
- •Точки разрыва
- •Транспонированная матрица
- •Треугольная матрица
- •Угловой коэффициент прямой
- •Угол между прямыми
- •Угол наклона прямой
- •Уравнение линии
- •Уравнение прямой в отрезках
- •Уравнение прямой с угловым коэффициентом
- •Уравнение, записанное в дифференциалах
- •Уравнение, разрешенное относительно производной
- •Условно сходящийся ряд
- •Условный экстремум
- •Фокальные радиусы гиперболы
- •Фокальные радиусы эллипса
- •Фокальный радиус параболы
- •Фокус параболы
- •Фокусы гиперболы
- •Фокусы эллипса
- •Формула Маклорена
- •Формула Тейлора
- •Функции спроса и предложения
- •Функциональный ряд
- •Функция Лагранжа
- •Функция выручки
- •Функция двух переменных
- •Функция издержек
- •Функция полезности двух товаров
- •Функция полезности
- •Функция прибыли
- •Функция спроса на товары
- •Функция
- •Центр гиперболы
- •Центр эллипса
- •Частичная сумма ряда
- •Частное и общее решения системы уравнений
- •Частное приращение функции
- •Частное решение дифференциального уравнения
- •Частные производные второго порядка
- •Частные производные
- •Четные и нечетные функции
- •Числовая функция
- •Числовой ряд
- •Эквивалентные бесконечно малые функции
- •Эквивалентные матрицы
- •Эквивалентные системы уравнений
- •Эксцентриситет гиперболы
- •Эксцентриситет эллипса
- •Эластичность функции двух переменных
- •Эластичность
- •Элементарные преобразования
- •Элементарные функции
- •Элементы матрицы
- •Эллипс
- •Эпсилон-окрестность на плоскости
- •Доказательства теорем
- •Часть II. Задачи
- •Глава 1. Аналитическая геометрия
- •1.1. Прямая на плоскости
- •1.1.1. Общие задачи
- •1.1.2. Экономика
- •1.2. Кривые второго порядка
- •1.2.1. Общие задачи
- •Глава 2. Теория пределов
- •2.1. Последовательность. Предел числовой последовательности
- •2.2. Функциональная зависимость
- •2.2.1. Общие задачи
- •2.2.2. Экономика
- •2.3. Предел функции. Два замечательных предела
- •2.4. Непрерывные функции
- •Глава 3. Теория дифференцирования
- •3.1. Производная. Вывод таблицы
- •3.3. Правила Лопиталя. Формула Тейлора
- •3.4. Исследование функции с помощью производной
- •Глава 4. Теория интегрирования
- •4.2. Интегрирование классов функций
- •4.3. Определенный интеграл
- •Глава 5. Дифференцирование функций двух переменных
- •5.1. Функция двух переменных. Дифференциал
- •5.1.1. Общие задачи
- •5.1.2. Экономический профиль
- •5.2. Экстремум функции двух переменных
- •5.2.1. Общие задачи
- •5.2.2. Экономический профиль
- •Глава 6. Дифференциальные уравнения
- •6.2. Дифференциальные уравнения первого порядка и их решение
- •Глава 7. Ряды
- •7.1. Числовые ряды
- •7.2. Функциональные ряды. Область сходимости
- •7.3. Степенные ряды. Формула Тейлора
- •Решения и указания
- •Ответы к задачам
- •Часть III. Тесты
- •Глава 1. Аналитическая геометрия
- •1.1. Прямая на плоскости
- •1.2. Кривые второго порядка
- •Глава 2. Теория пределов
- •2.1. Последовательности
- •2.2. Предел, непрерывность точки разрыва функции одной переменной
- •Глава 3. Теория дифференцирования
- •3.1. Дифференцирование функций одной переменной
- •3.2. Исследование функции одной переменной
- •Глава 4. Теория интегрирования
- •4.1. Неопределённый интеграл
- •4.2. Определённый интеграл с приложениями
- •Глава 5. Функции двух переменных
- •Глава 6. Дифференциальные уравнения
- •6.1. Элементарные дифференциальные уравнения
- •6.2. Линейные уравнения с постоянными коэффициентами
- •Глава 7. Ряды
- •7.1. Числовые ряды
- •7.2. Функциональные и степенные ряды
- •Глава 8. Линейная алгебра
- •8.1. Матрицы, определители, обратная матрица, системы уравнений
- •8.2. Векторная алгебра

Часть II. Задачи Решения и указания
Меню |
Назад Вперёд |
Решения и указания

Часть II. Задачи Решения и указания
Глава 1. Аналитическая геометрия
Меню |
Назад Вперёд |
Глава 1. Аналитическая геометрия

Часть II. Задачи Решения и указания
Глава 1. Аналитическая геометрия
Меню Решение задачи 2 Назад Вперёд
Решение задачи 2
Искомая точка имеет координаты (0; ). Применяя формулу (1.1) для нахождения расстояния между двумя точками, получаем и решаем уравнение для нахождения :
√
5 = (3 − 0)2 + (−8 − )2, 25 = 9 + (8 + )2, (8 + )2 = 16, |8 + | = 4.
Имеем два решения: 1 = −4 и 2 = −12. Итак, условию задачи удовлетворяют две точки: 1(0; −4) и 2(0; −12). [Вернуться к условию]

Часть II. Задачи Решения и указания
Глава 1. Аналитическая геометрия
Меню Решение задачи 10 Назад Вперёд
Решение задачи 10
Как известно, диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Тогда точка ( ; ) пересечения диагоналей может быть найдена как середина отрезка по формулам (1.3):
= |
2 + (−6) |
= |
− |
2, |
= |
4 + 6 |
= 5. |
|
2 |
2 |
|||||||
|
|
|
|
|
Обозначим через ( ; ) четвертую вершину параллелограмма. Тогда найденная точка (−2; 5) делит пополам диагональ . Применяя формулы середины отрезка (1.3), составляем и решаем уравнения для определения координат точки :
|
−3 + |
= |
− |
2, |
− |
3 + = |
− |
4, = 1; |
7 + |
= 5, |
7 + = 10, = 3. |
|
2 |
2 |
|||||||||||
|
|
|
− |
|
|
|||||||
Итак, четвертая вершина (−1; 3). |
|
|
[Вернуться к условию] |
|||||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Указание к задаче 13 |
Назад Вперёд |
Указание к задаче 13
Воспользуйтесь тем, что точка пересечения медиан делит медианы в отношении 2 : 1. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Указание к задаче 15 |
Назад Вперёд |
Указание к задаче 15
Воспользуйтесь тем, что по свойству биссектрисы внутреннего угла тре-
угольника |
|
= |
|
. |
[Вернуться к условию] |
|
|
||||
|
|
|
|
||

Часть II. Задачи Решения и указания
Глава 1. Аналитическая геометрия
Меню Решение задачи 18 Назад Вперёд
Решение задачи 18
Воспользуемся формулой (1.4) и найдем площадь треугольника с вершинами в данных точках:
1 |
|
|
1 |
|
|
|
||
= |
|
(5 − 2)(15 − 3) − (11 − 2)(7 − 3) = |
|
|
3 · 12 − 9 · 4 = 0. |
|
||
2 |
2 |
|
||||||
Площадь треугольника |
равна нулю. Это и означает, |
что его вершины |
лежат |
|||||
на одной прямой. |
|
|
|
|
[Вернуться к условию] |
|||

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 22.3 |
Назад Вперёд |
Решение задачи 22.3
Угол наклона данной прямой к оси равен 4 . Значит угловой коэффициент = tg 4 = 1. В уравнение прямой с угловым коэффициентом (1.5) подставляем значения = 1 и = −2:
= 1 · + (−2), |
= − 2. |
[Вернуться к условию]

Часть II. Задачи Решения и указания
Глава 1. Аналитическая геометрия
Меню Решение задачи 24 Назад Вперёд
Решение задачи 24
Угловой коэффициент данной прямой = tg arctg 3 = 3. Подставляем значение и координаты точки в уравнение (1.6):
− |
2 |
= 3( + 2), |
5 − 2 = 15 + 30, |
15 − 5 + 32 = 0. |
5 |
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 28.1 |
Назад Вперёд |
Решение задачи 28.1
Подставляем координаты точек и в уравнение (1.8): |
|
|
||||||||||||
|
− 7 |
= |
|
− 4 |
, |
− 7 |
= |
|
− 4 |
, |
− 7 |
= |
− 4 |
, |
|
4 − 7 |
|
−3 |
|
1 |
4 |
||||||||
|
|
−8 − 4 |
|
|
−12 |
|
|
|||||||
|
|
|
4( − 7) = − 4, |
|
4 − − 24 = 0. |
|
|
|||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 36.1 |
Назад Вперёд |
Решение задачи 36.1
Приведём данное уравнение к уравнению прямой с угловым коэффициентом:
|
|
|
|
2 |
|
1 |
|
||||
5 = −2 + 1, |
|
= − |
|
|
+ |
|
|
. |
|||
|
5 |
5 |
|||||||||
Из (1.5) следует, что |
2 |
|
|
1 |
|
|
|
|
|
||
= − |
, |
= |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
5 |
5 |
|
|
|
|
||||||
[Вернуться к условию]
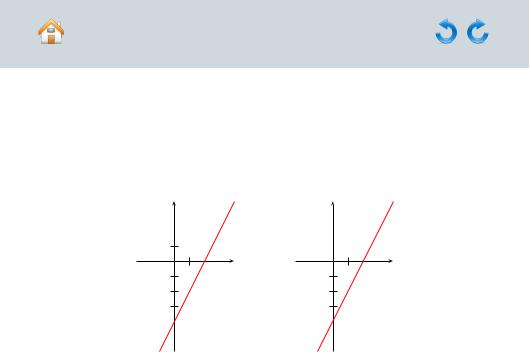
Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 40.1 |
Назад Вперёд |
Решение задачи 40.1
Чтобы построить прямую, достаточно знать координаты любых ее двух точек. Полагая = 0, получаем = −4, полагая = 1, получаем = −2. Имеем две точки (0, −4) и (1, −2). Проводим через них прямую (рисунок Р.1).
y |
|
1 |
|
O |
x |
b |
B |
b A |
|
Рисунок Р.1 |
|
y |
|
|
|
2 |
|
|
b |
x |
O |
|
|
−4 |
b |
|
|
|
|
Рисунок Р.2 |
|
|
Задачу можно решить иначе, преобразуя данное уравнение к уравнению прямой в отрезках:
2 − − 4 = 0, |
2 − = 4, |
2 |
− |
|
= 1, |
|
+ |
|
= 1. |
|||
|
|
|
|
|
|
|
||||||
4 |
4 |
2 |
−4 |
|||||||||
Теперь на оси отложим 2 единицы вправо, а на оси — 4 единицы вниз. Получаем две точки на осях координат, через которые проводим прямую (рисунок Р.2). [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 51.1 |
Назад Вперёд |
Решение задачи 51.1
Преобразуем данные уравнения прямых к уравнениям с угловым коэффициентом:
2 − 3 + 10 = 0, |
= |
2 |
+ |
10 |
; |
|
5 |
− + 4 = 0, |
= 5 + 4. |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
3 |
|
|
||||||||||||||
Выписываем угловые коэффициенты: 1 |
= |
2 , 2 = 5. Тогда по форму- |
||||||||||||||||||
ле (1.11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
5 |
− |
|
|
|
13 |
|
|
||||
tg = |
|
|
− 1 |
|
= |
|
|
|
|
|
|
= |
|
|
= 1. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 + 1 2 |
|
|
|
|
1 + 2 |
|
5 |
|
|
13 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Значит, угол между прямыми = |
|
. |
|
|
|
|
|
|
|
|
[Вернуться к условию] |
|||||||||
4 |
|
|
|
|
|
|
|
|||||||||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 59.1 |
Назад Вперёд |
Решение задачи 59.1
В силу параллельности искомая прямая и прямая имеют общий угловой коэффициент , который может быть вычислен по координатам точек ииз формулы (1.7):
= |
−1 − (−2) |
= |
1 |
= 1. |
|||
|
− |
|
|||||
|
4 |
− |
5 |
|
1 |
− |
|
|
|
|
|
||||
Итак, нам известны угловой коэффициент и точка искомой прямой. Выписываем ее уравнение по формуле (1.6):
− 1 = −1( − 3), |
+ − 4 = 0. |
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 60.1 |
Назад Вперёд |
Решение задачи 60.1
По формуле (1.7) вычисляем угловой коэффициент прямой :
= |
−5 − (−4) |
= |
−1 |
= 1. |
|
−4 − (−3) |
−1 |
||||
|
|
|
Согласно условию перпендикулярности двух прямых (1.13) угловой коэффициент искомого перпендикуляра
= − |
1 |
= − |
1 |
= −1. |
|
|
|
|
|||
|
1 |
||||
Зная точку и угловой коэффициент, выписываем искомое уравнение по формуле (1.6):
− 1 = −1( + 1), |
+ = 0. |
[Вернуться к условию]

Часть II. Задачи Решения и указания
Глава 1. Аналитическая геометрия
Меню Решение задачи 61 Назад Вперёд
Решение задачи 61
По формуле (1.7) находим угловой коэффициент стороны :
= |
5 − (−6) |
= |
|
11 |
. |
|
8 − 6 |
2 |
|||||
|
|
|
||||
Тогда угловой коэффициент искомой высоты
= − 1 = − 2 .
11
Зная угловой коэффициент и точку высоты, по формуле (1.6) выписываем ее уравнение:
− (−3) = − |
2 |
( − 2), |
11 + 33 = −2 + 4, |
2 + 11 + 29 = 0. |
11 |
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 67.1 |
Назад Вперёд |
Решение задачи 67.1
Найдем уравнение стороны по формуле (1.8):
− (−2) |
= |
− 5 |
, |
+ 2 |
= |
− 5 |
, |
+ 2 = |
− |
5, |
− |
+ 7 = 0. |
||||||||
|
|
|
− |
|
|
|||||||||||||||
− |
5 |
− |
− |
|
2 |
− |
5 |
|
|
|
− |
3 |
|
|
|
|
||||
|
|
( 2) |
|
|
|
3 |
|
|
|
|
|
|
|
|||||||
По формуле (1.14) вычислим высоту как расстояние от точки до пря-
мой : |
|
|
− √−12 + 12 |
|
|
√2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
8 (−5) + 7 |
= |
4 |
|
= 2√2. |
||||||
|
|
|
|
|||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию] |
||

Часть II. Задачи Решения и указания
Глава 1. Аналитическая геометрия
Меню Решение задачи 76 Назад Вперёд
Решение задачи 76
Обозначим первую из данных прямых через 1, а вторую — через 2. Пусть точка ( ; ) лежит на одной из искомых биссектрис. Тогда по свойству биссектрисы расстояние 1 от точки до прямой 1 равно расстоянию 2 от точки до прямой 2. По формуле (1.14) расстояния от точки до прямой
|
|
= |
|3 + 4 − 1| |
= |
|3 + 4 − 1| |
, |
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
√32 |
+ 42 |
|
|
|
|
|
5 |
|
|
||
|
|
= |
|5 + 12 − 2| |
= |
|
|5 + 12 − 2| |
. |
|||||||
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
√52 |
+ 122 |
|
|
|
|
13 |
|
|
|||
Тогда условие 1 = 2 порождает уравнение
|
|
|3 + 4 − 1| |
= |
|5 + 12 − 2| |
. |
|
|
|
|||||
|
|
|
|
|
5 |
|
|
|
13 |
|
|
|
|
Решаем его: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13|3 + 4 − 1| = 5|5 + 12 − 2|, |
|
|
|
||||||||
13(3 + 4 |
− |
1) |
= 5(5 + 12 − 2), |
14 − |
8 − 3 = 0, |
||||||||
[13(3 + 4 |
1) |
= |
− |
5(5 + 12 |
− |
2), |
[64 + |
112 |
− |
23 = 0. |
|||
|
− |
|
|
|
|
|
|
|
|
|
|||
Итак, мы нашли две биссектрисы: |
|
|
|
|
|
|
|
|
|||||
14 − 8 − 3 = 0, |
64 + 112 − 23 = 0. |
|
|
||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Указание к задаче 77 |
Назад Вперёд |
Указание к задаче 77
Найдите обе биссектрисы углов, образованных прямыми и . Затем выберите ту, от которой точки и находятся по разные стороны.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 79.1 |
Назад Вперёд |
Решение задачи 79.1
Найдем уравнение диагонали как уравнение прямой (1.8), проходящей через две точки:
|
− (−10) |
= |
|
− (−16) |
, |
|
+ 10 |
= |
+ 16 |
, |
|
+ 10 |
= |
|
+ 16 |
, |
||||||||||||
|
|
|
|
|
|
7 |
|
|
|
1 |
|
|
|
|
4 |
|||||||||||||
|
−3 − (−10) |
12 − (−16) |
28 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
4( + 10) = + 16, |
4 − + 24 = 0. |
|
|
|
|
|
|
|
|
|||||||||||||||
Аналогично найдем уравнение диагонали : |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
− (−15) |
|
= |
− (−2) |
, |
|
|
+ 15 |
= |
+ 2 |
, |
+ 15 |
= |
|
+ 2 |
, |
|
||||||||||
|
20 − (−15) |
|
|
|
|
|
5 |
|
|
|
||||||||||||||||||
|
|
|
19 − (−2) |
35 |
21 |
|
|
|
|
|
|
|
3 |
|
|
|||||||||||||
|
|
|
3( + 15) = 5( |
+ 2), |
3 − 5 + 35 = 0. |
|
|
|
|
|
|
|
|
|||||||||||||||
Для нахождения общей точки диагоналей составим из полученных уравнений систему, а затем решим ее:
|
4 − + 24 = 0, |
4 − + 24 = 0, |
|||||
Отсюда |
|
− |
5 + 35 = 0, |
− |
17 |
− |
85 = 0. |
|
3 |
|
|
|
|||
= −5, = 4 + 24 = 4 · (−5) + 24 = 4.
Итак, точка пересечения диагоналей четырехугольника имеет координаты (−5, 4). [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 102.1 |
Назад Вперёд |
Решение задачи 102.1
По условию ежегодная амортизация составляет 2,4 тыс. у. е. Тогда стоимость автомобиля через лет
12( ) = 24 − 5 .
Соответственно через 5 лет стоимость автомобиля будет равна
(5) = 24 − 125 · 5 = 12 тыс. у. е.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 106 |
Назад Вперёд |
Решение задачи 106
Для нахождения требуемого расстояния приравниваем транспортные расходы:
20 + 100 = 25 + 70, |
5 = 30, |
= 6. |
Итак, при перевозке на = 6 сотен километров транспортные расходы совпадают и составляют = 20 · 6 + 100 = 220 денежных единиц. Поэтому, начиная с 600 км, более экономичным становится первый вид транспорта.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 108 |
Назад Вперёд |
Решение задачи 108
По формуле (1.8) построим функцию издержек ( ), где — количество произведенной продукции, как прямую, проходящую через точки 1(8, 635)
и 2(13, 750):
( ) − 635 |
= |
− 8 |
, |
( ) − 635 |
= |
− 8 |
, |
( ) − 635 |
= |
− 8 |
, |
|
750 − 635 |
|
13 − 8 |
|
|
115 |
|
5 |
|
23 |
|
1 |
|
( ) − 635 = 23( − 8), |
( ) = 23 − 184 + 635 = 23 + 451. |
|
||||||||||
Функция выручки по условию имеет вид ( ) = 64 . Находим точку безубыточности как абсциссу точки пересечения линий издержек и выручки:
23 + 451 = 64 , |
41 = 451, |
= 11. |
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 112.1 |
Назад Вперёд |
Решение задачи 112.1
Равновесие на рынке определяется равенством спроса и предложения. С геометрической точки зрения точка рыночного равновесия — это точка пересечения линий спроса и предложения (смотрите рисунок Р.3):
+ 3 = −2 + 12, |
3 = 9, |
= 3. |
Таким образом, равновесная цена 0 = 3 денежные единицы, равновесный объем продаж 0 = 6 единиц.
y 
S
Q0 = 6
|
D |
|
|
|
|
O p0 = 3 |
x |
|
Рисунок Р.3 |
|
|
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 112.2 |
Назад Вперёд |
Решение задачи 112.2
Закон спроса не изменится, а закон предложения примет вид:
1 = + 3 = + 6.
Находим точку рыночного равновесия в новых условиях:
+ 6 = −2 + 12, |
3 = 6, |
= 2. |
Получена новая точка равновесия ′(2, 8). Следовательно, после введения налога равновесная цена увеличится на 2 единицы, а равновесный объем уменьшится на 1 единицу.
y |
|
|
S1 |
|
|
||||
|
|
|
||
Q0 = 8 |
|
|
S |
|
|
|
|
||
|
|
|
D |
|
|
|
|
|
|
O |
|
p0 = 2 |
x |
|
Рисунок Р.4 |
|
|
||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Указание к задаче 112.3 |
Назад Вперёд |
Указание к задаче 112.3
После введения субсидии закон спроса не изменится, а закон предложения примет вид:
= + 3 − .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Указание к задаче 112.4 |
Назад Вперёд |
Указание к задаче 112.4
Если налог составляет 20 %, то вся рыночная цена составляет 120 %, из них 100 % получают поставщики товара, 20 % — государство. После введения данного налога закон спроса не изменится, а закон предложения примет
вид:
120= 100( + 3).
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 119.2 |
Назад Вперёд |
Решение задачи 119.2
Выделяем полные квадраты в левой части уравнения:
( 2 −4 + 4) −4 + ( 2 + 8 + 16) −16 −16 = 0, ( −2)2 + ( + 4)2 −36 = 0.
Таким образом, центр окружности находится в точке (2, −4), ее радиус равен 6. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 126.2 |
Назад Вперёд |
Решение задачи 126.2
Найдем квадрат большой полуоси :
2 = 2 + 2 = 62 + |
(2) |
|
= 36 + 4 = |
4 |
= |
( 2 ) |
= 6,52. |
||
|
5 |
|
2 |
25 |
|
169 |
|
13 |
2 |
Следовательно, уравнение эллипса имеет вид:
2 |
2 |
|
|
|
+ |
|
= 1. |
6,52 |
62 |
||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 127.4 |
Назад Вперёд |
Решение задачи 127.4
Преобразуем уравнение к каноническому виду:
|
24 2 |
49 2 |
2 |
2 |
2 |
|
|
2 |
|
||||||||||||
|
|
+ |
|
= 1, |
|
+ |
|
= 1, |
|
|
+ |
|
|
|
|
= 1. |
|
|
|||
1176 |
1176 |
49 |
24 |
72 |
|
(2√ |
|
)2 |
|
||||||||||||
|
|
6 |
|
||||||||||||||||||
Отсюда следует, что |
|
|
|
|
|
|
|
|
√25 = 5, = |
= 7. |
|||||||||||
= 7, = 2√6, = √ 2 − 2 = √49 − 24 = |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
Координаты фокусов: 1(−5, 0), 2(5, 0). |
|
|
|
[Вернуться к условию] |
|||||||||||||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Указание к задаче 136.2 |
Назад Вперёд |
Указание к задаче 136.2
Касательной к эллипсу называется прямая, пересекающая эллипс в единственной точке. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 142.1 |
Назад Вперёд |
Решение задачи 142.1
Выделим полный квадрат по переменным и : |
|
|
|
|||||||
16( 2 |
− 4 + 4) − 64 − 9( 2 |
+ 6 + 9) + 81 − 161 = 0, |
||||||||
16( |
− |
2)2 |
− |
9( + 3)2 = 144, |
|
( − 2)2 |
− |
( + 3)2 |
= 1. |
|
9 |
16 |
|||||||||
|
|
|
|
|||||||
Отсюда следует, что центр гиперболы находится в точке (2; −3), действи-
√ √
тельная полуось = 9 = 3, мнимая полуось = 16 = 4.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 152.1 |
Назад Вперёд |
Решение задачи 152.1
Преобразуем данное уравнение к равносильному виду:
= 3√ |
|
, |
2 = 9 , |
|
|||
|
|
|
|
|
|
|
> 0. |
Полученная система уравнений определяет часть параболы 2 = 9 , лежащую в верхней полуплоскости, а точнее в первом квадранте.
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 154 |
Назад Вперёд |
Решение задачи 154
Проверим, нет ли у данных параболы и прямой общих точек. Для точек прямой имеет место равенство 4 = −3 − 44. Подставляя его в уравнение параболы, получим:
2 = 16 · (4 ), |
2 = 16(−3 − 44), |
2 + 48 + 704 = 0. |
Дискриминант данного квадратного уравнения, очевидно, отрицательный. Таким образом, данные парабола и прямая не пересекаются. В таком случае ближайшая к прямой точка параболы является общей точкой этой параболы и ее касательной, параллельной данной прямой. Такая касательная имеет уравнение
4 + 3 + = 0,
где константа подлежит определению. Касательная — это прямая пересекающая параболу в единственной точке, называемой точкой касания. Чтобы найти касательную, подберем число так, чтобы система уравнений
2 = 64 ,
4 + 3 + = 0
имела единственное решение. Из второго уравнения находим: 4 = −3 − . Подставляя это значение в первое уравнение, получим:
2 = 16(−3 − ), |
2 + 48 + 16 = 0. |
Данное квадратное уравнение имеет единственное решение, если его дискриминант равен нулю. На этом основании вычисляем :
242 − 16 = 0, = 242 = 42 · 62 = 36. 16 16
Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 154 |
Назад Вперёд |
Подставляя полученное значение обратно в квадратное уравнение, находим его решение:
2 + 48 + 16 · 36 = 0, ( + 24)2 = 0, = −24.
Подставляя найденное значение |
в уравнение параболы, находим : |
|
(−24)2 = 64 , |
82 · 32 = 64 , |
= 9. |
Итак, ближайшей к прямой 4 +3 +44 = 0 точкой параболы 2 = 64 является точка 0(9, −24). Вычисляем расстояние от точки 0 до данной
прямой: |
|4 · 9 + 3 · (−24) + 44| |
|
8 |
|
|||
= |
= |
. |
|||||
|
|
|
|
||||
|
√42 + 32 |
|
5 |
||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 159.1 |
Назад Вперёд |
Решение задачи 159.1
Выделяем полные квадраты и проводим преобразования:
( 2 + 2 + 1) − 1 − 9( 2 − 4 + 4) + 36 − 44 = 0,
( + 1)2 |
|
9( |
|
2)2 = 9, |
( + 1)2 |
( − 2)2 |
= 1. |
||
− |
− |
9 |
− |
1 |
|||||
|
|
|
|
||||||
Получили каноническое уравнение гиперболы с центром в точке (−1; 2). [Вернуться к условию]
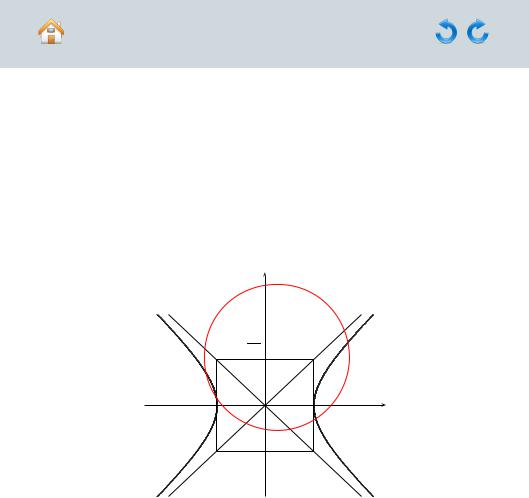
Часть II. Задачи Решения и указания
Глава 1. Аналитическая геометрия
Меню Решение задачи 160.1 |
Назад Вперёд |
Решение задачи 160.1
Приведем данное уравнение гиперболы к каноническому виду:
|
|
2 |
|
|
2 |
2 |
2 |
||||||||||
|
|
|
|
− |
|
|
= 1, |
|
|
− |
|
|
= 1. |
|
|
|
|
|
3648 |
|
3648 |
64 |
57 |
||||||||||||
|
57 |
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, для данной гиперболы |
|
|
|
|
|
|
|
|
|
||||||||
2 = 64, |
2 = 57, |
|
= √ |
|
= √ |
|
= √ |
|
= 11. |
||||||||
|
2 + 2 |
||||||||||||||||
|
64 + 57 |
121 |
|||||||||||||||
Значит, правый фокус гиперболы 2 = (11; 0) (смотрите рисунок Р.5).
y |
|
|
|
√57 |
C |
|
|
|
b |
|
|
|
8 |
F2 |
|
|
|
b |
|
O |
|
11 |
x |
|
|
|
|
Рисунок Р.5 |
|
|
|
Окружность с центром в точке (2; 8) имеет уравнение:
( − 2)2 + ( − 8)2 = 2,

Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 160.1 |
Назад Вперёд |
где радиус подлежит определению. Подставим в это уравнение координаты найденной ранее точки 2 по условию принадлежащей окружности:
(11 − 2)2 + (0 − 8)2 = 2, |
81 + 64 = 2, |
2 = 145. |
Итак, искомое уравнение окружности ( − 2)2 + ( − 8)2 = 145. [Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 161.2 |
Назад Вперёд |
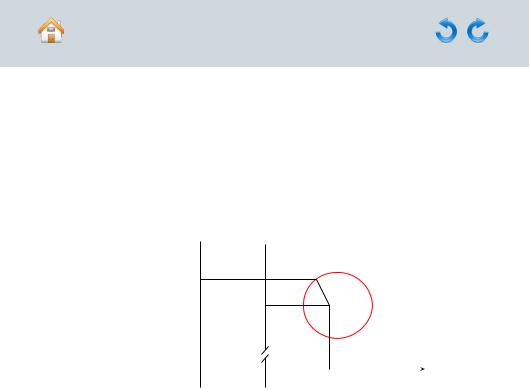
Решение задачи 161.2
расстояние между точками ( ; ) и , а также расстояние от точки до прямой = −1 могут быть вычислены по формулам:
|
|
|
|
|
|
= √ |
|
|
|
|
|
|
, |
|
= | + 1|. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
( − 1)2 + ( − 5)2 |
|
|
|
|
|
|||||||||||||||||||||||||||
Так как по условию 4 = , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
16(( − 1)2 + ( − 5)2) = ( + 1)2, |
||||||||||||||||||||||||||
4 ( − 1)2 |
+ ( − 5)2 = | + 1|, |
||||||||||||||||||||||||||||||||||||
√ |
16( |
2 |
|
|
+ 1 |
) |
− ( |
2 + 2 + 1 |
+ 16( |
|
5)2 |
= 0, |
|
||||||||||||||||||||||||
|
|
|
|
− |
2 |
2 |
|
|
|
|
|
|
) |
|
|
2 |
|
− |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
15 |
|
|
− 34 + 15 + 16( − 5) |
|
|
= 0, |
|
|
|
|
|
|
||||||||||||||||
15 |
( 2 − 2 · 15 + |
( |
15) ) |
− 15 |
|
+ 15 + 16( − 5)2 = 0, |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
17 |
|
2 |
172 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
2) |
|
|
|
|
|
|
|
|||
|
− |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
15 |
|
|
|
|
|
|
|
|
|
|
15 |
|
|
8 |
|
|
|
|
|
2 |
2 |
|
||||||||||||||
|
|
|
|
|
) |
2 |
+ 16( |
|
|
5)2 = |
64, |
|
|
|
15 |
1517 |
2 |
+ |
( |
√15 |
5)2 |
= 1. |
|||||||||||||||
|
15 |
|
17 |
|
|
|
|
|
− |
− |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
|
|
|
|
( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получено каноническое уравнение эллипса со следующими полуосями и цен-
тром: |
= √15, |
|
(15; 5). |
||||
= 15, |
|||||||
8 |
|
2 |
|
|
17 |
|
|
|
|
|
|
|
|
|
|
Чертеж полученного эллипса изображен на рисунке Р.6.
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 1. Аналитическая геометрия |
|
Меню Решение задачи 161.2 |
Назад Вперёд |
y 
dM
|
b |
r |
|
|
|
5 |
b |
b O |
|
|
A |
|
|
|
|
|
|
|
|
−1 |
O |
1 |
x |
|
|
Рисунок Р.6 |
|
|
|

Часть II. Задачи Решения и указания Глава 2. Теория пределов
Меню |
Назад Вперёд |
Глава 2. Теория пределов

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 162.2 |
Назад Вперёд |
Решение задачи 162.2
Подставляя в формулу общего члена значения = 1, 2, 3, 4, последовательно находим
|
|
= |
(−1)1 |
= |
− |
1, |
|
|
= |
(−1)2 |
= |
1 |
, |
|||
1 |
1 |
2 |
2 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
(−1)3 |
= |
− |
|
1 |
, |
|
|
= |
(−1)4 |
= |
1 |
. |
|
3 |
3 |
3 |
4 |
4 |
4 |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 162.8 |
Назад Вперёд |
Решение задачи 162.8
Общий член последовательности = ! представляет собой произведение всех натуральных чисел от 1 до :
! = 1 · 2 · 3 · . . . · ( − 2) · ( − 1) · .
Поэтому
1 = 1, |
2 = 1 · 2 = 2, |
3 = 1 · 2 · 3 = 6, |
4 = 1 · 2 · 3 · 4 = 24. |
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 162.11 |
Назад Вперёд |
Решение задачи 162.11
Данная последовательность задана рекуррентно: каждый последующий член последовательности вычисляется через предыдущий. Имеем:
1 = 1, |
2 = 1 + 2 = 1 + 2 = 3, |
3 = 2 + 2 = 3 + 2 = 5, |
4 = 3 + 2 = 5 + 2 = 7. |
|
[Вернуться к условию] |

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 164.8 |
Назад Вперёд |
Решение задачи 164.8
Так как для всякого N верно, что ограничена снизу. Так как, кроме того,
= |
+ 1 |
= 1 + |
1 |
|
|
|
|
||
|
|
|||
> 0, то последовательность { }
6 1 + 1 = 2,
то { } также ограничена сверху и, следовательно, ограничена. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 165.1 |
Назад Вперёд |
Решение задачи 165.1
В данном случае для всех натуральных
+1 = 2( + 1) + 1 = 2 + 3 > 2 + 1 = .
Поэтому последовательность строго возрастающая.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 165.2 |
Назад Вперёд |
Решение задачи 165.2
Найдём три первые элемента: |
|
|
|
|
|
|
1 = −1, |
2 = |
1 |
|
3 = − |
1 |
|
|
, |
|
. |
|||
2 |
3 |
|||||
Отсюда видно, что с одной стороны 1 < 2, а с другой — 2 > 3. Значит, данная последовательность не является монотонной.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 165.3 |
Назад Вперёд |
Решение задачи 165.3
Так как |
1 |
|
1 |
|
|
|
+1 = |
< |
|
= , |
|||
|
|
|
|
|||
( + 1)2 |
2 |
|||||
то данная последовательнось строго убывает. |
[Вернуться к условию] |
|||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 165.5 |
Назад Вперёд |
Решение задачи 165.5
В данном случае для всех натуральных |
|
|
+1 = [√ + 1] |
> [√ ] |
= . |
Следовательно, последовательность { } возрастает. Отсутствие строгого возрастания следует из того, что 1 = 2 = 1. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 169.1 |
Назад Вперёд |
Решение задачи 169.1
Пусть — произвольное положительное число. Тогда требование | | |
< |
|||||||||||||
влечёт за собой неравенства |
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
1 |
|
|
||||||
|
|
|
|
|
< , |
> |
|
|
. |
|
||||
|
|
|
|
|
||||||||||
Так как номер должен быть натуральным числом, положим |
|
|||||||||||||
|
|
|
= |
[ ] + 1. |
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
При > будем иметь |
[ |
] |
|
|
|
|
|
|
|
|
||||
|
|
+ 1 |
|
|
|
|||||||||
|
1 |
6 |
|
|
1 |
|
< |
1 |
= . |
|
||||
|
1 |
|
|
|
1 |
|
||||||||
Это и означает, что последовательность бесконечно малая.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 171.1 |
Назад Вперёд |
Решение задачи 171.1
Зададимся произвольным положительным числом и обозначим = |
|
. |
|||||||||||||||||||||||||||||||
−1 |
|||||||||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
− |
|
|
|
|
− |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||
| − | |
− |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 = |
|
|
|
|
|
1 |
|
= |
|
|
|
|
− 1) |
|
= |
|
|
− |
, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
1 |
|
|
|
|
|
||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
| − 1| < , |
|
|
1 |
|
|
|
|
|
|
|
− |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|||||||||
|
|
|
< , |
|
1 > |
|
, |
|
> 1 + |
|
. |
|
|
||||||||||||||||||||
|
|
− 1 |
|
|
|
|
|
|
|||||||||||||||||||||||||
Если теперь положить |
|
|
|
|
= |
[ |
] + 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то при всех > |
|
|
|
|
|
||||||||||||||||||||||||||||
окажется, что | − 1| |
|
< . А это и доказывает, что |
|||||||||||||||||||||||||||||||
последовательность сходится к единице. |
|
|
|
|
|
|
|
[Вернуться к условию] |
|||||||||||||||||||||||||
Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 172.4 |
Назад Вперёд |
Решение задачи 172.4
Вынесем из числителя и знаменателя в старшей, в данном случае второй, степени:
3 2 − + 2 |
|
2 |
|
3 − 1 + |
2 |
|
|
3 − 1 + |
2 |
|
. |
||||
= |
2 |
|
= |
2 |
|||||||||||
5 2 + 2 |
2 |
5 + |
2 |
|
|
|
5 + |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
||||||||
Теперь мы можем применить свойство 4 сходящихся последовательностей:
lim 3 2 − + 2 = lim |
3 − 1 + 22 |
= |
|
→∞ ( |
|
− |
|
|
|
2 ) |
= |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
3 |
|
1 |
+ |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
→∞ 5 2 + 2 |
|
|
|
2 |
|
|
|
|
|
|
→∞ (5 + 2 ) |
|
|
|
||||||||||||
→∞ |
5 + |
2 |
|
|
|
|
|
|
|
|
lim |
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
lim |
3 − lim |
1 |
+ |
lim |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
3 |
− |
0 + 0 |
|
3 |
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||
= |
|
→∞ |
→∞ |
|
|
|
|
|
|
→∞ |
|
|
= |
|
|
|
|
= |
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
5 + 0 |
5 |
|||||||||||||||
|
|
|
|
|
lim 5 + |
|
lim |
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
→∞ |
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Мы воспользовались тем, что предел константы — константа, а последовательности {1 } и { 12 } — бесконечно малые. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 172.14 |
Назад Вперёд |
Решение задачи 172.14
Используя определение факториала из задачи 162.8, разделим числитель и знаменатель на ( + 1)!:
lim |
( + 1)! + ( + 2)! |
= |
lim |
|
1 + ( + 2) |
= |
|
|
|
|
|
|
|
|||||
( + 3)! |
|
|
|
|
|
|
|
|
|
|
|
|||||||
→∞ |
|
|
→∞ ( + 2)( + 3) |
1 |
|
3 |
|
|
|
|
|
|
||||||
|
|
|
|
+ 3 |
|
|
|
|
+ |
|
|
|
|
0 + 0 |
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
= lim |
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
= |
|
= 0. |
|
|
|
|
|
|
|
|
|
|
5 + |
|
6 |
|
|
|||||
|
→∞ 2 |
+ 5 + 6 |
→∞ 1 + |
|
|
1 + 0 + 0 |
|
|||||||||||
|
2 |
|
||||||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 172.31 |
Назад Вперёд |
Решение задачи 172.31
Домножим и разделим выражение под знаком предела на сопряжённое к
нему, после чего применим к числителю формулу разности квадратов: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
+ 1 − + 1 = |
|
( |
|
|
|
|
|
|
|
− |
√ + 1)+( |
√ − 1 |
|
|
|
|
|
|
) |
= |
|
|
|
|
|
|||||||||||||||||||||||||
√ |
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
√ |
+ 1 |
|
|
√ |
− 1 |
|
√ |
+ 1 |
+ √ |
− 1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
( |
|
√ +)1 + |
( |
|
|
− 1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 1 + − 1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ 1 + − 1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
= |
|
|
√ |
+ 1 |
2 |
|
− |
|
√ |
− 1 |
|
2 |
= ( + 1) |
− ( − 1) |
= |
|
|
|
|
2 |
|
|
|
. |
|||||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
√ |
|
|
|
|
|
|
√ |
|
|
|
√ |
|
|
|
||||||
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
→∞ √ + 1 + √ − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
→∞ |
|
|
|
|
|
|
|
|
|
|
− |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||
lim |
|
√ |
+ 1 |
|
|
|
√ |
|
|
|
|
1 |
|
= |
|
lim |
2 |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
· √1 + 0 + √1 − 0 |
|
|
· |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
→∞ √ √1 + 1 + √1 − 1 |
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 |
|
|
= 0. |
|||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 172.34 |
Назад Вперёд |
Указание к задаче 172.34
Дополнить данное выражение до разности кубов, умножив и разделив его на сопряжённое ему выражение. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 172.38 |
Назад Вперёд |
Решение задачи 172.38
Вынесем, как всегда, из числителя и знаменателя в старшей степени:
|
√ |
|
|
|
3/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|||||||
lim |
√ |
|
|
= lim |
|
|
|
|
|
|
= lim |
· |
lim |
|
|
|
|
= ∞ · 1 = ∞. |
||
|
+ 1 |
1/2 |
|
|
1 |
|
|
1 |
|
|
||||||||||
|
|
|
||||||||||||||||||
→∞ |
|
|
|
|
|
→∞ |
|
1 + |
√ |
|
|
→∞ |
|
→∞ 1 + |
√ |
|
|
|||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 172.46 |
Назад Вперёд |
Указание к задаче 172.46
Привести дроби к общему знаменателю. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 172.51 |
Назад Вперёд |
Решение задачи 172.51
Применив формулу суммы арифметичекой прогрессии
1 + 2 + 3 + · · · + = ( + 1), 2
получим: |
+ 2· · · |
|
− 2 ) |
→∞ (2( + 2) |
|
− 2( + 2) ) |
|
|
|
|
|
||||||||||
→∞ ( |
+ |
|
= |
|
|
|
|||||||||||||||
|
1 + 2 + 3 + |
|
|
|
|
( + 1) |
|
|
( + 2) |
|
|
|
|
|
|||||||
lim |
|
|
|
|
= |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
− |
|
= lim |
|
−1 |
= |
−1 |
|
= |
− |
1 |
. |
|||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
→∞ 2 + 4 |
→∞ 2 + 4 |
2 + 0 |
|
2 |
|
|||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 172.54 |
Назад Вперёд |
Указание к задаче 172.54
Воспользуйтесь формулой
1 + 4 + 9 + · · · + 2 = ( + 1)(2 + 1). 6
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 172.58 |
Назад Вперёд |
Указание к задаче 172.58
Примените формулу суммы геометрической прогрессии
1 + + 2 + · · · + = 1 − +1 . 1 −
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 179 |
Назад Вперёд |
Решение задачи 179
Выясним, является ли эта последовательность монотонной. Действительно, запишем ( + 1)-й член:
∑+1 1
+1 = =1 + 1 + .
Сравним члены и +1. С этой целью преобразуем их следующим образом:
+1 |
1 |
|
|
|
|
−1 |
1 |
|
|
|
|
|
1 |
1 |
|
|
|||||
∑ |
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 = |
+ (1 + ) |
|
= |
|
+ (1 + ) |
+ |
|
2 + 1 |
+ |
2 + 2 |
, |
|
|||||||||
=1 |
1 |
|
|
−1 |
|
=1 |
|
|
1 |
|
|
−1 |
1 |
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|||||||||||||
∑ |
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
= |
|
|
= |
|
|
|
|
|
= |
|
|
|
+ |
|
. |
||||||
+ |
|
|
+ (1 + ) |
+ 1 |
+ (1 + ) |
||||||||||||||||
=1 |
|
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
Остается заметить, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
+ |
|
1 |
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
> |
|
. |
|
|
|
|
|||||||||
|
|
|
2 + 1 |
2( + 1) |
+ 1 |
|
|
|
|
||||||||||||
Таким образом, N < +1, т.е. последовательность возрастающая. Покажем, что она ограничена. Во-первых, очевидно, что N > 0.
Во-вторых, N |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
1 |
|
|
∑ |
|
|
∑ |
|
|
|
|
= |
+ |
< |
=1 |
|
= |
|
= 1. |
=1 |
|
|
|
|
|
|
|
Значит, N 0 < < 1.
Следовательно, последовательность { } является возрастающей, ограниченной и имеет предел. [Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 180 |
Назад Вперёд |
Решение задачи 180
Поскольку
√ √ √ √ √ √ √ √
= + + . . . + + 0 < + + . . . + + = +1,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 1 корней |
|||||
|
+ 1 |
корней |
|||||||
|
|
|
|||||||
то последовательность возрастает.
Докажем что ограничена сверху, например, числом деле, для первого элемента это верно:
√ √
1 = < + 1.
Для N имеет место представление
√
+1 = + ,
и, если предположить, что 6 √ + 1, то
+1 6 √ + √ + 1 < √ + 2√ + 1 = √(√ + 1)2
√ + 1. В самом
(Р.1)
√
=+ 1,
что и доказывает ограниченность всех элементов последовательности.
По теореме 2.4 возрастающая и ограниченная последовательность сходится. Обозначим ее предел через . Факт существования предела последовательности делает возможным предельный переход при → ∞ в рекуррентном равенстве (Р.1). В результате получаем и решаем уравнение отностительно :
= √ |
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
, |
2 = + , |
2 |
− |
|
− |
|
|
1 ± 1 + 4 |
. |
|||
+ |
|
= 0, |
= |
||||||||||
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 180 |
Назад Вперёд |
Итак, предел необходимо равен одному из двух полученных значений. Так как отрицательное значение не подходит, то
|
1 + √ |
|
. |
|
= |
1 + 4 |
|||
2 |
||||
|
|
|||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 184.1 |
Назад Вперёд |
Решение задачи 184.1
Подставим значение = 0 в аналитическое выражение данной функции:
√ √
(0) = 1 + 02 = 1 = 1.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 185.5 |
Назад Вперёд |
Решение задачи 185.5
В выражении функции заменяем на 1 :
|
( ) |
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
||||
|
1 |
|
|
1 |
+ 3 |
|
|
+ 3 2 |
3 2 |
+ |
|||||||||||
|
|
|
= |
|
|
|
|
|
|
= |
|
|
|
= |
|
|
|
|
|
. |
|
|
|
( |
1 |
) |
2 |
− |
|
|
− |
2 |
|
− |
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 186.5 |
Назад Вперёд |
Решение задачи 186.5
Заменяем на 3 в выражении функции ( ):
(3 ) = (3 )3 · 23 = 33 · 3 · (23) = 27 3 · 8 .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 187.2 |
Назад Вперёд |
Решение задачи 187.2
Так как логарифм задан для положительных значений аргумента, то область определения находится из условия:
2 +
2 −
> 0.
Этому условию удовлетворяет интервал (−2, 2). |
[Вернуться к условию] |

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 188.1 |
Назад Вперёд |
Решение задачи 188.1
Выделим полный квадрат:
= 2 + 4 + 4 − 3 = ( + 2)2 − 3.
Множеством значений функции = ( + 2)2 является промежуток [0, +∞). Так как ( ) = ( ) − 3, то для функции множество значений= [−3, +∞). [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 189.1 |
Назад Вперёд |
Решение задачи 189.1
Область определения ( ) = (−∞, +∞) симметрична относительно начала координат, и
( |
− |
) = |
(− )3 |
= |
− 3 |
= |
− |
( ). |
|
(− )2 + 1 |
2 + 1 |
||||||||
|
|
|
|
|
|||||
Следовательно, функция ( ) нечетная. |
|
|
|
[Вернуться к условию] |
|||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 189.3 |
Назад Вперёд |
Решение задачи 189.3
Здесь ( ) = (−∞, ∞), и
(− ) = − − 2 ̸= ± ( ).
Значит, функция ( ) не является как четной, так и нечетной, то есть имеет общий вид. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 190.1 |
Назад Вперёд |
Решение задачи 190.1
Основной период функции sin равен 2 . Функция ( ) = sin 4 получается из нее путем сжатия в 4 раза вдоль оси . Следовательно, функция ( ) периодическая, и ее основной период = 14 · 2 = 2 .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 190.2 |
Назад Вперёд |
Решение задачи 190.2
Так как |
|
|
1 + cos 10 |
|
1 |
|
|
1 |
|
|
|
|
|
|
cos2 |
5 = |
= |
+ |
|
cos 10 , |
|||||||
|
|
|
|
|
|
||||||||
|
2 |
2 |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|||
то функция |
периодическая и ее период = |
|
|
· 2 = |
|
. |
|||||||
10 |
5 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию] |
||

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 190.4 |
Назад Вперёд |
Указание к задаче 190.4
Убедитесь, период суммы двух периодических функций равен наименьшему общему кратному их периодов. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 191.4 |
Назад Вперёд |
Решение задачи 191.4
Функции ( ) определена на всей вещественной оси. Её областью значений является интервал (− 2 , 2 ). Выразим аргумент через значение функции :
= arctg 3 , |
tg = 3 , |
= |
1 |
tg . |
|||
|
|||||||
3 |
|||||||
Таким образом, = |
1 |
tg является искомой обратной функцией. |
|||||
3 |
|||||||
|
|
|
|
|
[Вернуться к условию] |
||
|
|
|
|
|
|
||

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 192.1 |
Назад Вперёд |
Решение задачи 192.1
Вычисляем искомые суперпозиции:
( ( )) = √ 2 = | |, ( ( )) = (√ )2 = , > 0.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 193.2 |
Назад Вперёд |
Решение задачи 193.2
Данная функция является суперпозицией линейной функции = 3 , тригонометрической функции = tg и логарифмической функции = lg .
[Вернуться к условию]
|
Часть II. Задачи |
|
|
|
|
|
|
Решения и указания |
|
|
|
|
|
|
Глава 2. Теория пределов |
|
|
|
|
|
Меню |
Решение задачи 194.11 |
|
|
|
Назад |
Вперёд |
|
Решение задачи 194.11 |
|
|
|
|
|
В качестве исходного возьмем график функции = cos (см. рисунок Р.7). |
||||||
|
y |
1 |
y |
= cos x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
π |
π |
|
|
|
|
|
2 |
|
|
|
|
|
O |
−1 |
3π |
5π |
x |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
Рисунок Р.7 |
|
|
|
|
|
С помощью сдвига вправо на величину = 4 получаем график функции = cos( − 4 ) (см. рисунок Р.8).
y |
|
y = cos(x − π4 ) |
|
|
1 |
3π |
5π |
|
|
|
4 |
4 |
|
|
O |
π |
7π |
11π |
x |
|
4 |
4 |
4 |
|
Рисунок Р.8 |
|
|
|
|
Растягивая полученный график в 2 раза вдоль оси , получаем требуемый график функции = 2 cos( − 4 ) (см. рисунок Р.9).
[Вернуться к условию]
Часть II. Задачи Решения и указания Глава 2. Теория пределов
Меню Решение задачи 194.11 |
Назад Вперёд |
y |
|
y = 2 cos(x − π4 ) |
|
|
2 |
|
|
|
|
|
3π |
5π |
|
|
|
4 |
4 |
|
|
O |
π |
7π |
11π |
x |
|
4 |
4 |
4 |
|
−2 |
|
|
|
|
Рисунок Р.9 |
|
|
|
|

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 194.16 |
Назад Вперёд |
Указание к задаче 194.16
Выделить полный квадрат в выражении под знаком модуля.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 194.19 |
Назад Вперёд |
Указание к задаче 194.19
Через [ ] обозначают целую часть числа . Для |
[ , + 1), где Z, |
целая часть [ ] = . |
[Вернуться к условию] |
Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 194.20 |
Назад Вперёд |
Решение задачи 194.20
Дробная часть числа определяется как разность самого числа и его целой части:
{ } = − [ ].
Так как значение дробной части не изменяется при изменении числа на любое целое значение, то достаточно построить часть графика функции= { } на полуинтервале [0, 1), а затем путём сдвигов влево и вправо на целочисленные значения аргумента получить весь график. Если [0, 1), то [ ] = 0 и потому { } = . На рисунке Р.10 изображён получающийся в итоге график. [Вернуться к условию]
y |
|
|
|
|
1 |
|
|
|
|
−4 −3 −2 −1 O 1 |
2 |
3 |
4 |
x |
|
||||
Рисунок Р.10 |
|
|
|
|

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 194.22 |
Назад Вперёд |
Указание к задаче 194.22
Воспользуйтесь тем, что cos2 = 12 (1 + cos 2 ). [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 194.23 |
Назад Вперёд |
Указание к задаче 194.23
Воспользуйтесь тем, что
sin4 + cos4 = (sin2 + cos2 )2 − 2 sin2 cos2 .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 194.26 |
Назад Вперёд |
Указание к задаче 194.26
Проведите построение графика |
отдельно для промежутков (−∞, −2], |
[−2, −1], [−1, 0] и [0, +∞). |
[Вернуться к условию] |

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 195.6 |
Назад Вперёд |
Указание к задаче 195.6
См. задачу 194.19. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 196 |
Назад Вперёд |
Решение задачи 196
Находим равновесную цену:
( 0) = |
( 0), |
|
|
25 0 |
+ 4 02 |
= |
20 + 4 02 |
, |
|
|
|
|
|||||||||||||||
|
|
|
1 + 10 0 |
|
|
1 + 10 0 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
25 + 4 2 |
= 20 + 4 2 |
, |
|
25 |
|
= 20, |
|
= |
4 |
. |
|
||||||||||||||||
0 |
|
|
|||||||||||||||||||||||||
0 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
5 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Находим равновесный объем продаж: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
20 + 4 |
( |
4 |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
500 + 64 |
|
|
|
564 |
|
|
188 |
|
||||||||||||||
0 = ( 0) = |
5 |
|
= |
|
= |
= |
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
4 |
|
|
|
|
225 |
75 |
|||||||||||||||||
|
|
|
|
|
|
|
|
25 + 200 |
|
|
|
|
|
||||||||||||||
|
|
|
1 + 10 · |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 199.1 |
Назад Вперёд |
Решение задачи 199.1
Зафиксируем произвольное > 0 и найдём такое > 0, что для всех , удовлетворяющих условию 0 < | − 0| < , выполнялось бы неравенство
|
(2 + 1) − 5 < . |
|
|
|
|
|
|
|||
Решая последнее неравенство, |
получаем, |
что |
|
|
|
|
|
|
||
|
|
|
|
< , |
|
|
|
|||
|
|
|
|
|||||||
|
|
|||||||||
2 − 4 < , |
2( − |
2) |
− 2 < |
2. |
||||||
Для завершения доказательства достаточно принять = |
|
|
. |
|||||||
2 |
||||||||||
|
|
|
|
|
|
[Вернуться к условию] |
||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 199.11 |
Назад Вперёд |
Указание к задаче 199.11
Воспользуйтесь тем, что по определению предела, стремясь к числу = 1, переменная не принимает этого значения. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 200.1 |
Назад Вперёд |
Решение задачи 200.1
Рассмотрим функцию ( ) = 3 2 + 2 − 1. Выберем произвольным образом последовательность { } такую, что
lim = 2, ̸= 2 ( N).
→∞
Найдем предел последовательности ( ), пользуясь свойством 4 сходящихся последовательностей:
lim ( ) = |
lim (3 2 + 2 − 1) = |
|
|
|
→∞ |
→∞ |
|
→∞ − 1 = 3 · 2 + 2 · 2 − 1 = 15. |
|
|
( →∞ ) |
2 |
||
|
= 3 lim |
+ 2 lim |
2 |
|
|
|
|||
В силу произвольности выбора последовательности { } искомый предел равен 15. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 201.1 |
Назад Вперёд |
Решение задачи 201.1
Рассмотрим последовательности |
= 2 и |
= + 2 , сходящиеся к |
0 = ∞. Для них |
|
|
lim ( ) = |
lim cos 2 = |
lim 1 = 1, |
|
|
|
|
||
→∞ |
→∞ |
( |
→∞ |
→∞ |
− |
|
− |
|
→∞ ( ) = |
→∞ |
) |
1) = |
1. |
||||
lim |
lim cos |
+ 2 = |
lim ( |
|
|
|||
Пределы последовательностей { ( )} и { ( )} оказались различными. Это значит, что предел функции не существует. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 202.2 |
Назад Вперёд |
Решение задачи 202.2
По свойствам предела арифметических операций
|
|
3 2 |
− |
1 |
|
|
lim1(3 2 − 1) |
|
|
|
|
|
|
|
|||||
lim |
|
|
|
= |
|
|
→− |
|
|
|
= |
|
|
|
|
|
|||
|
|
|
|
|
lim (4 2 |
+ 5 + 2) |
|
|
|
|
|
||||||||
→−1 4 2 + 5 + 2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
lim1 3 2 − |
|
→−1 |
|
|
|
|
lim1 · |
|
|
− 1 |
|
||||||
|
|
lim1 1 |
|
|
|
3 |
lim1 |
|
|||||||||||
= |
|
→− |
|
|
|
→− |
|
= |
|
|
→− |
→− |
|
|
= |
||||
lim1 4 2 |
+ lim1 |
5 + lim1 2 |
4 lim1 |
· lim1 |
+ 5 |
lim1 + 2 |
|||||||||||||
|
|
→− |
|
→− |
|
|
|
→− |
|
|
→− |
→− |
|
|
|
→− |
|
||
|
|
|
|
|
|
= |
|
|
3 · (−1) · (−1) − 1 |
|
= |
|
3 − 1 |
= 2. |
|||||
|
|
|
|
|
|
|
4 · (−1) · (−1) + 5 · (−1) + 2 |
4 − 5 + 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 202.6 |
Назад Вперёд |
Решение задачи 202.6
Свойство предела частного здесь неприменимо, поскольку в точке = 3 знаменатель обращается в нуль. Числитель не обращается в нуль в этой точке, что позволяет найти предел «перевернутой дроби»:
lim |
− 3 |
= |
0 − 3 |
= 0. |
|
2 + 5 |
2 · 3 + 5 |
||||
→3 |
|
|
Итак, мы доказали, что функция ( ) = 2 −+53 бесконечно малая. Тогда по теореме 2.7 функция 1/ ( ), то есть функция под знаком предела, является бесконечно большой, и ее предел равен ∞.
Вышесказанное позволяет при решении примеров для сокращения записи проводить формальное деление ненулевой константы на нуль, получая в результате бесконечность:
lim |
2 + 5 |
= |
2 · 3 + 5 |
= |
11 |
= . |
|||||
|
− |
|
|
|
|||||||
→ |
3 |
|
3 |
|
3 |
− |
3 |
|
0 ∞ |
||
|
|
|
|
|
|||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 202.11 |
Назад Вперёд |
Решение задачи 202.11
В точке = 2 как числитель, так и знаменатель обращаются в нуль. Это значит, что мы имеем неопределённость вида 00 . Для её раскрытия разложим числитель и знаменатель на множители, а затем сократим их общий множитель:
lim |
2 − 4 |
= lim |
( − 2)( + 2) |
= lim |
+ 2 |
. |
2 − 5 + 6 |
( − 2)( − 3) |
|
||||
→2 |
→2 |
→2 |
− 3 |
|||
Знаменатель последней дроби теперь не обращается в нуль, что позволяет применить свойства предела арифметических операций:
|
+ |
2 |
|
lim ( + |
2) |
2 |
+ 2 |
|
4 |
|
|||||||
|
|
→2 |
|
|
|
= −4. |
|||||||||||
lim2 |
|
|
|
= |
|
|
= |
|
|
|
= |
|
|
||||
|
− |
3 |
lim ( |
− |
3) |
2 |
− |
3 |
− |
1 |
|||||||
→ |
|
|
|
|
→ |
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 202.15 |
Назад Вперёд |
Решение задачи 202.15
Здесь, очевидно, имеем неопределенность вида 00 . Для ее раскрытия разложим числитель и знаменатель на множители:
lim |
4 2 + 23 + 15 |
= lim |
|
( + 5)(4 + 3) |
|
|
= |
|
|
|
|
|
|
|
|
|
||||||||||
−7 2 − 36 − 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
→−5 |
→−5 ( + 5)(−7 − 1) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
= lim |
|
|
4 + 3 |
= |
4 · (−5) + 3 |
= |
−17 |
= |
|
1 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
→− |
5 |
− |
7 |
− |
1 |
− |
7 |
· |
( |
− |
5) |
− |
1 |
34 |
|
−2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 202.31 |
Назад Вперёд |
Решение задачи 202.31
В точке = 1 числитель и знаменатель рассматриваемой дроби обращаются в нуль, поэтому имеем неопределенность вида 00 . Так как число = 1 является корнем многочленов в числителе и знаменателе, то последние делятся без остатка на − 1. Выполним деление «уголком»:
|
3 2 − − 2 |
|
− 1 |
|
|
3 − 2 + 4 − 4 |
|
− 1 |
|||||||
− |
3 2 − 3 |
|
|
− 3 − 2 |
|
|
|||||||||
|
3 + 2 |
|
2 + 4 |
||||||||||||
|
− |
2 − 2 |
|
|
|
|
|
− 4 − 4 |
|
|
|
||||
|
|
2 − 2 |
|
|
|
|
|
|
|
4 − 4 |
|
|
|
||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
3 2 |
− − 2 |
= lim |
( − 1)(3 + 2) |
= |
|
|
||||||
|
|
|
|
|
|||||||||||
|
|
3 − 2 + 4 − 4 |
|
|
|
|
|||||||||
|
→1 |
|
→1 |
( − 1)( 2 + 4) |
|
|
|||||||||
|
|
|
|
|
|
= lim |
3 + 2 |
= |
3 · 1 + 2 |
= 1. |
|||||
|
|
|
|
|
|
2 + 4 |
|
||||||||
|
|
|
|
|
|
→1 |
12 + 4 |
|
|
|
|||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 202.39 |
Назад Вперёд |
Решение задачи 202.39
Подставляя значение = 1 в числитель и знаменатель, убеждаемся, что имеем неопределённость вида 00 . Для её раскрытия избавимся от иррациональности в числителе, домножая числитель и знаменатель на выражение, сопряжённое числителю:
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
)( |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
||||
→ |
|
|
|
|
|
|
→ |
|
|
|
|
( 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
lim |
√ |
+ 8 |
− 3 |
|
= lim |
|
√ |
+ 8 |
− 3 |
|
|
√ + 8 + 3 |
= |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
− |
1 |
|
|
+ 8 |
|
|
9− |
|
( |
|
|
|
|
|
|
|
|
) |
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
√ + 8 + 3 |
|
|
(√1 + 8 + 3) |
|
|
|
|
|
|||||||||||||||
|
|
|
→1 |
( − 1) |
(√ + 8 + 3) |
|
1 →1 ( − 1) |
1 |
|
1 |
|
|||||||||||||||||||||||||||||
|
|
= lim |
|
|
|
|
|
|
|
− |
|
|
|
|
√ |
|
|
= lim |
|
|
√ |
|
− |
|
|
|
= |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
= lim1 |
|
|
|
|
= |
|
|
|
= |
|
|
= |
|
|
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + 3 |
6 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
+ 8 + 3 |
1 + 8 + 3 |
|
|
||||||||||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 202.51 |
Назад Вперёд |
Решение задачи 202.51
Имеем неопределенность вида 00 . Избавимся от иррациональности в числителе, разложим на множители знаменатель и сократим общий множитель:
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
)( |
|
|
|
|
|
|
|
|
|
|
|
) |
|||||||||
|
|
|
|
|
|
|
|
|
( + 2)( + 3) |
|
|
|
|
|
|
+ 7 |
|||||||||||||||||||||||
√ |
2 + 9 |
− √ |
+ 7 |
= |
|
√2 + 9 − √ + 7 |
|
|
|
√2 + 9 + |
√ + 7 |
|
= |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
= |
|
|
|
(2 + 9) − (( + 7) |
+ 9 + √ |
|
= |
) |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
+ 5 + 6 |
|
|
|
|
|
|
|
|
|
|
|
|
√2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
( + 2 |
( |
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
+ 2)( + 3) |
|
√2 + 9 + |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
= |
|
(√ |
|
+ √ |
|
) |
|
= |
( + 3) |
(√ |
|
+ √ |
|
) |
||||||||||||||||||||||||
|
( + 2)( + 3) |
2 + 9 |
+ 7 |
|
2 + 9 |
+ 7 |
|||||||||||||||||||||||||||||||||
Полученная дробь не содержит неопределенности, так что нахождение предела сводится к простой подстановке значения = −2:
√√
lim |
2 + 9 − |
+ 7 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 + 5 + 6 |
|
|
|
|
|
|
|
|
|||||||||
→−2 |
|
|
|
|
|
|
|
|
|
√ |
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
1 |
|
5 |
|
|
||||
|
= |
|
|
|
|
|
|
= |
|
2√ |
|
= |
|
. |
|||
|
(−2 + 3) (√ |
|
+ √ |
|
) |
10 |
|||||||||||
|
|
|
|
|
5 |
||||||||||||
|
|
2 · (−2) + 9 |
|||||||||||||||
|
|
|
−2 + 7 |
|
|||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 202.59 |
Назад Вперёд |
Указание к задаче 202.59
Положить = 12. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 202.60 |
Назад Вперёд |
Указание к задаче 202.60
Пользуясь формулой
3 − 3 = ( − )( 2 + + 2),
дополнить числитель до разности кубов. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 202.62 |
Назад Вперёд |
Решение задачи 202.62
В данном случае имеем неопределённость вида ∞∞ . Для её раскрытия применим стандартный приём. Вынесем из числителя и знаменателя в старшей степени, а затем воспользуемся тем, что функции 1 и 12 бесконечно малые при → ∞:
|
1 + − 2 |
|
|
|
2 |
|
|
1 |
+ 1 − 1 |
= lim |
|
|
1 |
+ 1 − 1 |
= |
|
|||||||||||||
lim |
= |
|
lim |
|
2 |
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
→∞ |
2 2 + 3 |
|
→∞ |
2 |
|
|
|
|
2 + 3 |
) |
→∞ |
|
2 + 3 |
|
|
|
|
|
|||||||||||
|
|
|
|
lim |
( |
1 |
|
+ 1 − 1 |
lim |
1 |
+ lim |
1 − |
lim 1 |
||||||||||||||||
|
|
= |
|
|
2 |
|
|
= |
2 |
||||||||||||||||||||
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
|
|
→∞ |
|
|
|
→∞ = |
|||||
|
|
|
|
0 + 0 |
|
(1 |
|
3 |
)1 |
|
|
|
|
→∞ |
|
→∞ |
1 |
|
|||||||||||
|
|
|
|
lim |
|
2 + |
|
|
|
|
|
|
lim 2 + 3 lim |
|
|||||||||||||||
|
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= |
|
|
− |
|
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 + 3 |
· |
0 |
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 202.75 |
Назад Вперёд |
Решение задачи 202.75
Выражение в скобках представляет собой неопределенность вида ∞ − ∞. Умножим и разделим функцию под знаком предела на выражение, сопряженное разности в скобках:
|
→ ∞ |
|
(√ |
|
|
|
|
|
) |
|
|
|
→ ∞ |
( |
|
|
|
|
|
+)( |
|
|
|
|
|
|
|
) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
√ 2 + 1 |
− |
|
|
√ 2 |
+ 1 + |
|
|
|
|
|
||||||||||||||
|
lim |
|
|
|
2 |
|
|
|
|
= |
lim |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
+ 1 |
− |
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|||||||||||||
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
2 |
|
1 + |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
= lim |
( |
|
+ 1 − |
) |
= lim |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
→+∞ |
√ 2 + 1 + |
|
|
|
→+∞ √ 2 + 1 + |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
= |
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= →+∞ √1 + 1/ 2 + 1 = √1 + 0 + 1 |
2. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 203.1 |
Назад Вперёд |
Решение задачи 203.1
Приведём данный предел к первому замечательному:
lim |
sin 2 |
= lim 2 |
sin 2 |
= 2 lim |
sin 2 |
. |
|
2 |
|
||||
→0 |
→0 |
→0 |
2 |
|||
Так как при → 0 функция 2 является бесконечно малой, то последний предел является первым замечательным и, таким образом,
lim |
sin 2 |
= 1. |
|
2 |
|||
→0 |
|
||
Значит, искомый предел равен 2. |
|
[Вернуться к условию] |

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 203.2 |
Назад Вперёд |
Решение задачи 203.2
Воспользуемся первым замечательным пределом и свойствами пределов:
|
|
6 |
sin 6 |
|
|
sin 6 |
|
|
lim |
sin 6 |
|
|
|
|
||
|
sin 6 |
6 |
|
|
|
6 |
|
6 |
|
1 |
|
|||||
lim |
= lim |
|
|
= lim 3 |
|
|
= 3 |
→0 |
= 3 |
= 3. |
||||||
|
|
|
|
|
|
|
|
|
||||||||
→0 sin 2 |
→0 2 |
sin 2 |
|
→0 |
sin 2 |
|
|
lim |
sin 2 |
|
1 |
|
||||
2 |
|
|
2 |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
→0 |
|
|
|
|
|||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 203.3 |
Назад Вперёд |
Решение задачи 203.3
Сделаем замену = arcsin . Так как |
= sin и → 0 |
при → 0, то |
|||||||||||||||
lim |
arcsin |
= lim |
|
= lim |
1 |
|
|
= |
|
1 |
|
|
= |
1 |
= 1. |
||
|
|
|
sin |
|
|
sin |
|
|
|||||||||
→0 |
|
→0 sin |
→0 |
|
|
lim |
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
→0 |
|
|
|
|
|
|
||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 203.5 |
Назад Вперёд |
Указание к задаче 203.5
Представить тангенс как отношение синуса и косинуса и воспользоваться тем, что
lim cos = 1.
→0
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 203.6 |
Назад Вперёд |
Указание к задаче 203.6
Воспользоваться формулой 1 − cos = 2 sin2 2 . [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 203.7 |
Назад Вперёд |
Решение задачи 203.7
Данное выражение содержит неопределенность вида 0 |
. Преобразуем его к |
|||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
виду, содержащему первый замечательный предел: |
|
|
|
|
|
|
||||||||
lim |
cos 5 − cos3 5 |
= lim |
cos 5 (1 − cos2 5 ) |
|
= lim |
cos 5 sin2 5 |
= |
|||||||
2 |
|
|
2 |
|
|
|||||||||
→0 |
|
→0 |
2 |
→0 |
|
|
|
|
||||||
|
= →0 |
|
· |
(5 )2 |
→0 |
· ( →0 |
|
5 |
) |
2 |
|
|
||
|
lim 25 cos 5 |
|
sin2 5 |
= lim 25 cos 5 |
lim |
sin 5 |
|
= |
|
|||||
|
|
|
|
|
|
|
|
|
||||||
= 25 cos 0 · 12 = 25.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 203.11 |
Назад Вперёд |
Решение задачи 203.11
Воспользуемся формулой
|
|
|
cos |
− |
cos = |
− |
2 sin |
+ |
sin |
− |
. |
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
Тогда имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
lim |
cos 5 − cos 3 |
= lim |
−2 sin 4 sin |
= |
− |
8 lim |
sin 4 sin |
= |
− |
8. |
||||||||||||
2 |
|
4 |
|
|
||||||||||||||||||
|
→ |
0 |
|
|
→ |
0 |
|
2 |
|
|
|
0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 203.15 |
Назад Вперёд |
Решение задачи 203.15
Имеем неопределенность вида |
0 |
. Избавимся от иррациональности в числи- |
|||||||||||||||||||||||
теле: |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2 sin2 |
|
|
|
|
||
|
cos − 1 |
|
|
|
|
cos |
− 1 |
|
|
|
|
|
|
||||||||||||
lim |
|
= lim |
|
|
= lim |
|
|
|
|
2 |
|
= |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
→0 |
= 1 |
lim |
|
sin(2 |
|
|
|
lim |
|
) |
1 |
= |
( |
1 |
12 |
+ 1 |
)1 |
= 1. |
|||||||
|
2 |
−2 |
→0 |
2 |
√cos + 1 |
|
→0 |
2 |
√cos |
|
|
−4 |
|||||||||||||
|
|
|
→0 |
( |
2 |
|
) |
2 |
→0 |
√cos + 1 |
|
− |
2 · |
|
· √1 + 1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 203.19 |
Назад Вперёд |
Решение задачи 203.19
Выполним замену переменной = − 2 . Новая переменная , как того и требует первый замечательный предел, будет стремится к нулю. Поэтому
|
|
2 |
|
|
|
→ |
2 |
( |
2 |
|
) |
→ |
|
|
|
→ |
|
|
|
|
|
lim |
cos |
= lim |
cos |
|
+ |
2 |
= lim |
− sin |
= |
1 |
lim |
sin |
= |
|
1 |
. |
|||||
|
− |
|
( |
|
|
) |
− |
|
|
|
|
||||||||||
|
→ |
2 |
|
0 |
+ |
0 |
2 |
−2 0 |
|
−2 |
|||||||||||
|
|
|
|
|
|
||||||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 203.25 |
Назад Вперёд |
Указание к задаче 203.25
Положить = arctg − 2 . [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 204.1 |
Назад Вперёд |
Решение задачи 204.1
Имеем неопределённость 1∞. Чтобы привести данный предел ко второму замечательному (2.7), выполним замену = . Ясно, что → 0 при → ∞. Тогда имеем
→∞ (1 + ) |
= |
→0 |
( →0 |
) |
|
|
|
|
|
|
1 |
|
|
lim |
|
|
lim (1 + ) = |
lim (1 + ) |
|
= . |
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 204.2 |
Назад Вперёд |
Указание к задаче 204.2
Обозначить = . [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 204.3 |
Назад Вперёд |
Решение задачи 204.3
Приводим данный предел ко второму замечательному:
→0 |
|
→0 |
= →0 |
( →0 |
|
) |
||
lim √ |
|
|
|
|
|
|
5 |
|
|
1 |
lim (1 + 5 ) |
1 |
·5 = |
lim (1 + 5 ) |
1 |
. |
|
1 + 5 = lim (1 + 5 ) |
5 |
5 |
||||||
Так как функция ( ) = 5 бесконечно малая при → 0, то по формуле (2.7)
1 |
|
|
|
lim (1 + 5 ) |
5 |
= . |
|
→0 |
|
|
|
А это значит, что искомый предел равен 5. |
[Вернуться к условию] |
||

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 204.6 |
Назад Вперёд |
Решение задачи 204.6
Приведём данный предел к отношению двух вторых замечательных, поделив числитель и знаменатель на , и воспользуемся задачей 204.1:
→∞ |
( − 2) |
|
lim |
+ 3 |
|
|
|
|
|
|
|
1 + |
3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
= lim |
|
|
|
|
= lim |
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
→∞ |
|
|
|
|
|
|
|
→∞ |
||||||
|
|
1 − |
|
|
|
|
|
||||||||
= →∞ (1 + ) |
|
= 3 |
|||||||||||||
|
|
lim |
|
|
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
( |
|
|
|
|
) |
|
|
|
−2 |
|||||
|
|
lim |
1 + |
−2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
(1 |
+ ) |
= |
|||
|
|
3 |
|
|
|
(1 |
− ) |
|
|
||
|
2 |
|
|
|
|
= 5.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 204.12 |
Назад Вперёд |
Решение задачи 204.12
Имеем неопределенность вида 1∞. Выражение в скобках преобразуем к сумме единицы и БМФ, что позволит нам воспользоваться вторым замечательным пределом в форме (2.7):
→∞ |
( − 3) |
|
|
= |
→∞ ( |
|
− 3 |
− 1) |
= |
|
|
|
|
|
|
|
|||||||||
lim |
|
+ 5 |
2 +7 |
|
lim |
|
1 + |
+ 5 |
|
|
2 +7 |
|
|
|
|
|
|
|
|||||||
|
→∞ ( |
|
|
|
|
( |
|
|
− 3) |
|
|
|
|
|
|
|
|||||||||
|
|
|
− 3) |
|
|
= →∞ |
|
|
8 |
|
· −3 |
· |
|
= |
|||||||||||
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
+7 |
|
|
|
|
|
|
|
−3 |
|
8 |
|
(2 +7) |
|
||
|
= lim |
|
1 + |
|
|
|
|
|
|
|
lim |
1 + |
|
|
|
|
|
|
|
|
|
lim |
16 +56 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
8 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
1 + |
|
|
|
−8 3 →∞ |
−3 . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||||||||||
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|||
Так как функция ( ) = |
|
|
является бесконечно |
малой при → ∞, то |
|||||||||||||||||||||
− |
3 |
||||||||||||||||||||||||
по формуле (2.7) предел в основании степени равен . Предел в показателе степени, очевидно, равен 16. Значит, искомый предел равен 16.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 204.22 |
Назад Вперёд |
Указание к задаче 204.22
Сделать замену = sin . [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 204.23 |
Назад Вперёд |
Указание к задаче 204.23
Воспользоваться формулой
cos 2 = 1 − 2 sin2 .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 205.1 |
Назад Вперёд |
Решение задачи 205.1
Так как функция ( ) = является бесконечно малой при → 0, то
lim |
− 1 |
= lim |
· |
− 1 |
= lim |
− 1 |
= |
· |
1 = . |
|||||
|
|
|
||||||||||||
|
→ |
0 |
0 |
|
→ |
0 |
|
|
||||||
|
|
|
→ |
|
|
|
|
|
|
|
|
|||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 205.2 |
Назад Вперёд |
Решение задачи 205.2
Воспользуемся следствиями первого и второго замечательного предела:
|
|
|
|
3 |
− 1 |
|
|
|
|
|
3 |
− 1 |
|
|
|
|
|
3 |
− 1 |
|
|
|
|
|
|
|
|
|
|
lim |
|
|
= 6 lim |
|
|
2 |
|
= 6 lim |
|
lim |
2 |
|
= 6 |
· |
1 |
· |
1 = 6. |
||||||||||||
|
tg |
|
3 |
tg |
|
|
3 |
|
|
||||||||||||||||||||
|
→ |
0 |
|
|
→ |
0 |
|
0 |
|
→ |
0 tg |
|
|
|
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
→ |
|
|
|
|
|
2 |
|
|
|
|
|
||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 205.5 |
Назад Вперёд |
Указание к задаче 205.5
В знаменателе вынести за скобки . [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 205.10 |
Назад Вперёд |
Решение задачи 205.10
Преобразуем данное выражение: |
|
|
|
|
|
|
|
|
|
|||||
= lim1 |
ln 2 |
|
= lim1 |
ln( 2 − 1 + 1) |
|
= |
lim1 |
ln(( 2 − 1) + 1) |
|
2 − 1 |
= |
|||
− 1 |
|
|
2 |
− 1 |
||||||||||
→ |
→ |
− 1 |
|
|
→ |
− 1 |
|
|
||||||
= lim1 |
ln(( 2 |
− 1) + 1) |
lim1 |
2 − 1 |
. |
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|||||||
→ |
− 1 |
→ |
− 1 |
|
|
|
|
|
|
|
||||
Так как функция ( ) = 2 − 1 является бесконечно малой при → 1, то искомый предел
= 1 · lim ( + 1) = 2.
→1
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 205.17 |
Назад Вперёд |
Решение задачи 205.17
Воспользуемся тем, что ( ) = − 1 — БМФ при → 1: |
|
|
|
|
|
|||||||||||||||||||||||||
→1 |
2 |
−1 |
= →1 √ |
|
|
|
|
|
|
|
− |
|
|
2 |
− 1 = |
|
|
|
|
|
||||||||||
|
|
− |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
= lim |
√3 |
|
|
1 |
|
lim |
|
3 |
|
( |
|
1) + 1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
||||||
√ |
|
− |
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
− |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
→1 |
|
|
− |
|
1 |
|
|
|
→1 |
2− |
1 |
|
|
3 · |
→1 + 1 3 |
· 2 |
6 |
|||||||||||||
|
3 ( |
|
1) + 1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
1 |
|
|
1 |
1 |
1 |
|||||||||
= lim |
|
|
|
|
|
− |
|
|
|
|
|
|
lim |
|
|
− |
|
= |
|
|
lim |
|
= |
|
|
= |
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 205.19 |
Назад Вперёд |
Указание к задаче 205.19
√
В числителе вынести за скобку 4 1 + 2. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 206.1 |
Назад Вперёд |
Решение задачи 206.1
Так как sign = 1 при > 0 |
и sign = −1 |
при < 0, то |
|||||||
→+0(2 sign |
− |
1) = →+0( |
2 |
· |
1 |
− |
1 |
) |
|
lim |
|
) |
lim |
|
|
= 1, |
|||
→−0( |
− |
→−0(2 · (−1) − 1) = −3. |
|||||||
lim 2 sign |
|
1 |
= lim |
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 206.6 |
Назад Вперёд |
Решение задачи 206.6
Для данной функции
1 |
0 |
1 0 |
( |
− |
2) = 1 |
− |
2 = |
− |
lim |
( ) = |
lim |
|
|
1, |
|||
→ − |
|
→ − |
|
|
|
|
|
|
lim ( ) = |
lim |
ln = ln 1 = 0. |
|
|||||
→1+0 |
→1+0 |
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 207.1 |
Назад Вперёд |
Решение задачи 207.1
Находим предел отношения данных функций, используя первый замечательный предел:
→0 |
2 |
→0 |
2 |
→0 |
( |
2 |
|
) |
2 |
|
( →0 |
2 |
|
) |
2 |
|
|
lim |
1 − cos |
= lim |
2 sin2 2 |
= lim |
|
sin |
2 |
|
= |
lim |
sin |
2 |
|
= 1. |
|||
2 |
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как предел равен 1, то 1−cos |
2 |
при → 0. |
[Вернуться к условию] |
||||||||||||||
2 |
|||||||||||||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 208.1 |
Назад Вперёд |
Решение задачи 208.1
Так как функции 4 и 3 являются бесконечно малыми при → 0, то sin 4 4 и sin 3 3 при → 0. Поэтому
lim |
sin 4 |
= lim |
4 |
= |
|
4 |
. |
|
3 |
3 |
|||||
→0 sin 3 |
→0 |
|
|
||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 208.12 |
Назад Вперёд |
Решение задачи 208.12
Так как 1 = ln , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ln − 1 = ln − ln = ln = ln (1 + − 1). |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Функция |
( ) = |
− 1 |
бесконечно малая при |
→ , поэтому |
|||||||||||||||||
|
|
||||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
ln |
(1 + − 1) − 1, |
→ . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Значит, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ln − 1 |
|
|
|
− 1 |
|
= |
1 |
. |
|
||||||
|
|
|
|
|
lim |
|
= lim |
|
|
||||||||||||
|
|
|
|
|
− |
− |
|
|
|||||||||||||
|
|
|
|
→ |
→ |
|
|||||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 208.16 |
Назад Вперёд |
Указание к задаче 208.16
Воспользоваться тем, что arctg( − 2) − 2 при → 2.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 208.18 |
Назад Вперёд |
Решение задачи 208.18
Воспользуемся таблицей эквивалентностей и задачей 207.1:
lim |
( 2 − 1) |
= lim |
· 2 |
= lim |
|
3 |
|
|
= 1. |
2 sin − sin 2 |
2 sin (1 − cos ) |
|
|
2 |
|||||
→0 |
→0 |
→0 |
· · |
|
|||||
|
|
|
|
2 |
|
|
|
||
|
|
|
|
2 |
|
|
|||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 212.1 |
Назад Вперёд |
Решение задачи 212.1
Будучи элементарной, данная функция непрерывна во всех точках своей области определения, т.е. в точке = 0. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 212.2 |
Назад Вперёд |
Решение задачи 212.2
Область определения данной функции ( ) = R. Поскольку функция ( ) является элементарной, то она непрерывна для всех ( ) = R.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 213.1 |
Назад Вперёд |
Решение задачи 213.1
Найдём односторонние пределы в точке 0 и сравним их со значением ( 0):
|
lim |
0 |
( ) = |
lim0 0 = 0 ̸= (0), |
|
lim |
( ) = |
|
lim 1 = 1 = (0). |
||
→− |
→ |
+0 |
→ |
+0 |
|||||||
|
|
|
→− |
|
|
|
|
|
|||
Отсюда следует, что функция ( ) |
непрерывна справа в точке 0. В силу |
||||||||||
различия значений односторонних пределов она не является непрерывной в этой точке. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 214.1 |
Назад Вперёд |
Решение задачи 214.1
Находим односторонние пределы в точке 0:
( 0 − 0) = (−0) = |
1 |
= −1, |
( 0 + 0) = (+0) = (0 + 1)2 = 1. |
0 − 1 |
Оба предела существуют и конечны, но различны. Следовательно 0 является точкой конечного скачка, причём скачёк равен
(+0) − (−0) = 2.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Указание к задаче 214.12 |
Назад Вперёд |
Указание к задаче 214.12
Символом [ ] обозначается целая часть числа . [Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 217.1 |
Назад Вперёд |
Решение задачи 217.1
Если | |
|
| |
< |
, то ( ) совпадает с элементарной функцией |
= sin и по- |
||
|
|
2 |
|
функция ( ) также непрерывна, поскольку |
|||
тому непрерывна. Для | | > |
2 |
||||||
совпадает с элементарной функцией = 1/2. Таким образом, исследовать
на непрерывность |
функцию ( ) следует в точках = |
± |
. |
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|
||
В точке = |
2 |
|
|
|
|
|
|
|
|
|
|
lim ( ) = |
lim sin = 1, |
lim ( ) = |
|
lim |
1 |
= |
1 |
. |
|||
|
|
|
|
||||||||
|
|
|
|
→ |
|
2 |
2 |
||||
→ 2 −0 |
|
→ 2 −0 |
→ 2 +0 |
2 +0 |
|||||||
Итак, односторонние пределы в точке = 2 существуют, конечны и не равны между собой. Следовательно функция ( ) в этой точке терпит конечный
разрыв со скачком |
( |
|
− 0) − |
( |
|
+ 0) = |
1 − 2 |
= 2. |
||
= |
2 |
2 |
||||||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Аналогичным образом убеждаемся, что в точке = − 2 функция ( ) также имеет конечный разрыв со скачком = 1/2. Строим график (рисунок Р.11).
|
|
y |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
− |
π |
O |
π |
x |
2 |
|
2 |
|
|
|
|
−1 |
|
|
|
|
Рисунок Р.11 |
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 217.12 |
Назад Вперёд |
Решение задачи 217.12
Если | | < 1, то |
|
lim |
|
|
|
|
|
0 |
|
|
|
|
|
||||
( ) = |
|
→∞ |
= |
|
|
|
= 0. |
||||||||||
|
|
|
|
|
|
||||||||||||
|
1 + 0 |
||||||||||||||||
|
|
1 + lim |
|
|
|
|
|
|
|
||||||||
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||
Если | | > 1, то |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
( ) = lim |
|
|
|
|
|
= |
|
|
|
|
= 1. |
||||||
|
|
|
|
|
0 + 1 |
||||||||||||
→∞ 1/ + 1 |
|
|
|
|
|
|
|||||||||||
При = 1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
||
( ) = lim |
= |
|
|
|
= |
. |
|||||||||||
|
|
1 + 1 |
|
2 |
|||||||||||||
|
→∞ 1 + 1 |
|
|
|
|
|
|
|
|||||||||
При = −1 знаменатель задающей функцию ( ) дроби для нечетных обращается в нуль. Значит, в этой точке предел не существует, и функция( ) не определена.
Итак, мы доказали, что
0 |
при | | < 1, |
|
|
|
|
|
|
( ) = 1/2 |
при = 1, |
|
|
|
при | | > 1. |
1 |
Так как
(1 − 0) = 0, |
(1 + 0) = 1, |
(−1 − 0) = 1, |
(−1 + 0) = 0, |
то эта функция в точках = ±1 терпит конечный разрыв со скачком = 1. В остальных точках функция ( ) совпадает с постоянной функцией и потому непрерывна. Строим чертеж (рисунок Р.12).
[Вернуться к условию]

Часть II. Задачи Решения и указания Глава 2. Теория пределов
Меню Решение задачи 217.12 |
Назад Вперёд |
|
y |
|
|
|
1 |
|
|
|
1 |
|
|
|
2 |
|
|
−1 |
O |
1 |
x |
|
|
||
Рисунок Р.12 |
|
|
|

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 218.1 |
Назад Вперёд |
Решение задачи 218.1
При = 0 функция ( ) совпадает с элементарной функцией 2−1/ 2 и потому |
|||||||
̸ |
|
|
|
|
|
|
|
непрерывна. Исследуем функцию ( ) на непрерывность в точке = 0: |
|||||||
lim ( ) = lim 2− |
1 |
= 2−∞ = 0 = 2 = (0). |
|||||
2 |
|||||||
|
→ |
0 |
|
→ |
0 |
|
̸ |
|
|
|
|||||
Итак, предел функции ( ) в точке = 0 существует, но не равен значению функции в этой точке. Таким образом, в точке = 0 данная функция имеет устранимый разрыв. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 2. Теория пределов |
|
Меню Решение задачи 221 |
Назад Вперёд |
Решение задачи 221
Функция ( ) = 4−3 2+2 −1 является многочленом и потому непрерывна на отрезке [1; 2]. Найдем ее значения на концах этого отрезка:
(1) = 1 − 3 + 2 − 1 = −1 < 0, (2) = 16 − 12 + 4 − 1 = 7 > 0.
Полученные значения имеют разные знаки, поэтому по первой теореме
Больцано—Коши существует точка |
(1; 2), в которой ( ) = 0. Число |
и есть корень данного уравнения. |
[Вернуться к условию] |

Часть II. Задачи Решения и указания
Глава 3. Теория дифференцирования
Меню |
Назад Вперёд |
Глава 3. Теория дифференцирования

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 229.1 |
Назад Вперёд |
Решение задачи 229.1
Воспользовавшись правилами дифференцирования суммы и разности, производной степенной функции, получим
′ = ( 3 + 3 2 − 4)′ = ( 3)′ + (3 2)′ − (4)′ = 3 2 + 3( 2)′ − 0 =
=3 2 + 3 · 2 = 3 2 + 6 .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 230.1 |
Назад Вперёд |
Решение задачи 230.1
Воспользуемся правилом дифференцирования сложной функции и таблицой производных. Получим
′ = (tg2 |
3 )′ = 2 tg 3 · (tg 3 )′ = 2 tg 3 · |
1 |
|
· (3 )′ = |
|
|
||
|
|
|
|
|||||
cos2 3 |
|
|
||||||
|
= 2 tg 3 · |
1 |
· 3 = |
6 tg 3 |
||||
|
|
|
|
. |
||||
|
|
cos2 3 |
cos2 3 |
|||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 231.1 |
Назад Вперёд |
Решение задачи 231.1
Применим формулу
′ = · (ln )′.
Найдем логарифмическую производную. При этом воспользуемся свойством логарифма.
ln = ln(sin ) = · ln sin ;
(ln )′ = ( · ln sin )′ = ′ · ln sin + · (ln sin )′ = ln sin + · cossin .
Подставим в исходную формулу
′ = (sin ) (ln sin + ctg ).
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 232.1 |
Назад Вперёд |
Решение задачи 232.1
Пользуясь правилами дифференцирования и таблицей производных, найдем:
′ = |
((4 − 3 5)5 + 4 ln 4) |
= |
5(4 − 3 5)− 5 |
· (−15 4) + 4 ln 4 · ln 4 = |
||||||||||||
|
1 |
2 |
|
|
′ |
1 |
|
|
4 |
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 4 |
||
|
|
|
|
|
|
|
= − |
|
|
+ 2 · 4 . |
||||||
|
|
|
|
|
|
|
√5 |
|
||||||||
Теперь вместо подставим 1: |
|
|
|
|
(4 − 3 5)4 |
|||||||||||
|
′(1) = |
|
3 · 14 |
+ 2 |
|
41 |
= |
|
3 + 8 = 5. |
|
|
|||||
|
−√5 (4 − 3 · 15)4 |
· |
− |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 233.1 |
Назад Вперёд |
Решение задачи 233.1
Найдем производную первого порядка:
′ = (3 2 − + 5)′ = 6 − 1.
Производную второго порядка найдем по определению
′′ = ( ′)′ = (6 − 1)′ = 6.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 234.1 |
Назад Вперёд |
Решение задачи 234.1
Используя определение, находим последовательно производные:
′ = (5 2 − 104 − 3)′ = 10 − 104,
′′ = ( ′)′ = (10 − 104)′ = 10,
′′′ = ( ′′)′ = (10)′ = 0.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 235.1 |
Назад Вперёд |
Решение задачи 235.1
Найдем первую и вторую производные указанной функции:
′ = ( − )′ = − − ,
′′ = (− − )′ = − .
Несложно сделать предположение, что
( ) = (−1) − .
Проверим справедливость этой формулы методом математической индукции.
При = 1 формула очевидно верна.
Пусть это равенство выполняется при = , т.е.
( ) = (−1) − .
Проверим его при = + 1, т.е. покажем, что
( +1) = (−1) +1 − .
Действительно,
( +1) = ( ( ))′ = ((−1) − )′ = (−1) · (−1) − = (−1) +1 − .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 236.1 |
Назад Вперёд |
Решение задачи 236.1
Прежде всего заметим, что
|
′ = 1, |
( )( ) = 0, = 2, 3, . . . , |
|||||
|
(sin )( ) = sin ( + |
|
). |
|
|
||
|
2 |
|
|
||||
Тогда, применяя формулу Лейбница, получим |
|
||||||
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
( sin )(100) = |
100( )( )(sin )(100− ) = |
|
|
||||
|
=0 |
|
|
|
|
|
|
|
= 1000 (sin )(100) + 1001 ′(sin )(99) = |
||||||
= sin( + 50 ) + 100 sin ( + 2 |
) |
= sin − 100 cos . |
|||||
|
|
|
|
99 |
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 237.1 |
Назад Вперёд |
Решение задачи 237.1
Уравнение касательной имеет вид:
= ′( 0)( − 0) + ( 0).
В нашем случае
′( ) = (ln )′ = 1 ,
′( 0) = ′(1) = 11 = 1,
( 0) = (1) = ln 1 = 0.
Подставив полученные результаты в уравнение касательной, получим
= 1 · ( − 1) + 0, |
т.е. |
= − 1. |
||||||
Уравнение нормали имеет вид: |
|
|
|
|
||||
1 |
|
|
|
|
|
|||
= − |
|
( |
− 0) + ( 0). |
|||||
′( 0) |
||||||||
Значит, в нашем случае уравнение нормали |
|
|
|
|||||
1 |
|
|
|
т.е. |
|
|
|
|
= − |
|
( − 1) + 0, |
= − + 1. |
|||||
1 |
||||||||
Определим угол наклона касательной |
|
|
|
|||||
tg = ′( 0) = 1 |
= |
|
||||||
|
. |
|||||||
4 |
||||||||
Сделаем рисунок.
[Вернуться к условию]
Часть II. Задачи Решения и указания
Глава 3. Теория дифференцирования
Меню Решение задачи 237.1 |
Назад Вперёд |
y |
y = x − 1 |
|
|
|
|
|
|
||
|
|
y = ln x |
|
|
|
b |
|
|
|
O |
1 |
y = |
−x |
x |
|
|
+ 1 |
||
|
Рисунок Р.13 |
|
||
Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 258.1 |
Назад Вперёд |
Решение задачи 258.1
Углом между кривыми в точке их пересечения называется угол между касательными к этим кривым в указанной точке.
Вначале определим точки пересечения данных кривых. Для этого ре-
шим систему уравнений
2 = 2 ,
2 + 2 = 8,
откуда получим точки (2; 2), (2; −2).
Рассмотрим вначале точку (2; 2). Для того, чтобы найти угол между касательными, достаточно знать их угловые коэффеценты в этой точке. Для
кривой 2 = 2 получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
||
2 · ′ = 2, |
|
′ = |
|
, |
|
|
1 |
= ′(2; 2) = |
|
|
. |
|||||
|
|
|
2 |
|||||||||||||
Для кривой 2 + 2 = 8 имеем |
|
|
|
|
|
|
|
|
|
|
|
|||||
2 + 2 · ′ = 0, |
′ = − |
|
, |
2 = ′(2; 2) = −1. |
||||||||||||
|
||||||||||||||||
|
||||||||||||||||
Значит для искомого угла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
1 |
= |
|
2 − 1 |
= |
|
−1 − 21 |
= |
− |
1, |
|
|
|
|||
|
|
1 + 21 |
|
|
|
|||||||||||
|
|
1 − 1 2 |
|
|
|
|
|
|
|
|||||||
т.е. острый угол между данными кривыми в точке (2; 2) равен |
. |
|||
Поступая аналогично для точки (2; −2), будем иметь |
4 |
|||
|
||||
1 |
|
|
|
|
1 = − |
|
, |
2 = 1, |
|
2 |
|
|||

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 258.1 |
Назад Вперёд |
|
1 + 1 |
|
|
|
|
tg 2 = |
2 |
= 1 |
2 = |
|
. |
1 + 1 |
4 |
||||
|
2 |
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 259.1 |
Назад Вперёд |
Решение задачи 259.1
Функция средних издержек выражается соотношением:
( ).
В данном случае
( ) = 50 − 0, 05 3 = 50 − 0, 05 2.
При = 10 средние издержки равны
( ) = 50 − 0, 05 · 102 = 45.
Функция предельных издержек выражается производной:
( ) = ′( ).
В данном случае
( ) = (50 − 0, 05 3)′ = 50 − 0, 15 2.
При = 10 предельные издержки равны
( ) = 50 − 0, 15 · 102 = 35.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 260.1 |
Назад Вперёд |
Решение задачи 260.1
Эластичность определяется с помощью следующей формулы:
|
|
|
|
|
|
( ) = |
|
′. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Значит, в данном случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
( ) = |
|
|
( |
− |
0, 5 + 80)′ = |
|
−0, 5 |
= |
|
|
|
. |
|||||||
|
0, 5 + 80 |
|
0, 5 + 80 |
|
|
|||||||||||||||
|
|
− |
|
|
|
|
|
|
|
|
− |
|
− |
160 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При = 60 эластичность себестоимости равна |
|
|
|
|
|
|
||||||||||||||
|
|
|
60( ) = |
|
60 |
|
|
= −0, 6. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
60 |
− |
160 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 261.1 |
Назад Вперёд |
Решение задачи 261.1
Производительность труда определяется производной от объема продукции:
( ) = ′( ).
Скорость изменения производительности выражается производной от производительности труда:
( ) = ′( ).
Темп изменения производительности равен логарифмической производной от производительности труда:
|
|
|
|
|
( ) = (ln ( ))′ = |
|
′( ) |
. |
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|||||
Значит, в данном случае |
+ 100 + 50) |
|
|
= −2 2 + 15 + 100, |
||||||||||||||
( ) = |
(−6 3 |
+ 2 2 |
′ |
|||||||||||||||
|
|
5 |
|
15 |
|
|
|
|
5 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
+ 15 + 100) |
|
|
|
|
|
||||
|
( ) = |
(−2 |
2 |
|
= −5 + 15, |
|||||||||||||
|
|
|
|
5 |
|
|
|
|
|
′ |
|
|||||||
|
( ) = |
|
−5 + 15 |
= |
|
2 − 6 |
. |
|||||||||||
|
|
|
2 − 6 − 40 |
|||||||||||||||
|
|
|
|
−25 |
2 + 15 + 100 |
|
|
|
|
|
||||||||
Через час после начала работы, т.е. при = 1, указанные параметры равны
5(1) = −2 + 15 + 100 = 112, 5,
(1) = −5 + 15 = 10,
(1) = |
|
2 − 6 |
= |
4 |
. |
1 |
− 6 − 40 |
|
|||
|
|
45 |
|||

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 261.1 |
Назад Вперёд |
За час до окончания работы, т.е. при = 8 − 1 = 7, указанные параметры равны
|
5 |
· 72 + 15 · 7 + 100 = 82, 5, |
||||||||
(7) |
= − |
|
||||||||
2 |
||||||||||
|
(7) = −5 |
· 7 |
+ 15 = −20, |
|||||||
|
(7) = |
2 |
· 7 |
− 6 |
= |
− |
8 |
. |
||
72 − 6 · 7 − 40 |
33 |
|||||||||
|
|
|
|
|
||||||
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 262.1 |
Назад Вперёд |
Решение задачи 262.1
Равновесная цена определяется из условия = . Поэтому, решив уравнение
+ 8
+ 2 = + 0, 5,
получим = 2, т.е. равновесная цена равна 2. Эластичность спроса определяется формулой
( ) = ′( ) = |
|
( + 2) |
′ |
= −( + 2)( + 8). |
||
|
|
|
+ 8 |
|
6 |
|
Эластичность предложения определяется формулой
( ) = |
|
′( ) = |
|
( + 0, 5)′ = |
|
|
= |
2 |
. |
|
|
|
+ 0, 5 |
2 + 1 |
|||||||
|
|
|
|
|
||||||
Значит, эластичность спроса и предложения для равновесной цены= 2 равна
|
( ) = |
− |
6 · 2 |
= |
− |
0, 3; |
( ) = |
|
2 · 2 |
= 0, 8. |
|
2 |
|
(2 + 2)(2 + 8) |
|
2 |
|
2 |
· |
2 + 1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 263.1 |
Назад Вперёд |
Решение задачи 263.1
Найдем производную: |
|
|
|
|
|
|
|
|
|
|
|
|
′ = (arcsin 2 )′ = |
√ |
1 |
|
|
|
· (2 )′ = |
√ |
2 |
|
. |
||
|
|
|
|
|||||||||
1 − 4 |
2 |
1 − 4 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
||||
Значит, дифференциал функции будет равен |
|
|
|
|
|
|
||||||
= ′ = |
√ |
2 |
|
. |
|
|
|
|||||
1 − 4 |
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 264.1 |
Назад Вперёд |
Решение задачи 264.1
Воспользуемся формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( + |
) − ( ) ≈ ′( ) · . |
|
|
|
|||||||||||||||||||
В этом случае ( ) = √ |
|
, ′( ) = |
1 |
|
|
|
. При применении указанной формулы |
||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2√ |
|
|
|
|
|
|
|
|
√ |
|
|
|||
важно правильно выбрать точку и |
|
|
. Легко вычислить |
25 |
= 5. Поэтому, |
||||||||||||||||||
в качестве положим 25, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
= 25, |
= 26 − 25 = 1. |
|
|
|
|
||||||||||||||||
Подставив их в формулу, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
√ |
|
|
|
|
|
√ |
|
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
25 + 1 − |
25 ≈ |
2√ |
|
· 1. |
|
|
|
|
||||||||||||
|
|
|
25 |
|
|
|
|
||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
√ |
|
|
√ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
26 = 25 + 1 ≈ |
|
+ 5 = 5, |
1. |
|
|
|
||||||||||||||||
|
10 |
|
|
|
|||||||||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 264.2 |
Назад Вперёд |
Решение задачи 264.2
Воспользуемся формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
( + |
) − ( ) ≈ ′( ) · . |
||||||||||||||||
В этом случае ( ) = √ |
|
, ′( ) = |
|
1 |
|
|
. При применении указанной формулы |
||||||||||
|
|||||||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
2√ |
|
. Легко вычислить √ |
|
|
||||||
важно правильно выбрать точку и |
|
1 |
= 1. Поэтому, |
||||||||||||||
в качестве положим 1, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 1, |
|
|
= 1, 2 − 1 = 0, 2. |
||||||||||||||
Подставив их в формулу, получим |
|
|
|
|
|
|
|
|
|||||||||
√ |
|
|
|
|
√ |
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||||
|
|
1 + 0, 2 − |
1 ≈ |
2√ |
|
· 0, 2. |
|||||||||||
|
|
1 |
|||||||||||||||
Тогда |
√ |
|
|
|
|
|
|
|
|
1, 2 ≈ 0, 1 + 1 = 1, 1. |
|
|
|
|
[Вернуться к условию] |
Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 264.3 |
Назад Вперёд |
Решение задачи 264.3
Воспользуемся формулой |
|
|
|
|
( + |
) − ( ) ≈ ′( ) · . |
|||
В этом случае ( ) = log2 , ′( ) = |
1 |
|
. При применении указанной фор- |
|
ln |
2 |
|||
мулы важно правильно выбрать точку |
и . Легко вычислить log2 2 = 1. |
|||
Поэтому, в качестве положим 2, т.е. |
|
|
||
= 2, |
= 1, 9 − 2 = −0, 1. |
|||
Подставив их в формулу, получим
1
log2(2 − 0, 1) − log2 2 ≈ 2 ln 2 · (−0, 1).
Тогда
1 log2 1, 9 ≈ 1 − 20 ln 2.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 266.1 |
Назад Вперёд |
Решение задачи 266.1
Так как sin 2 · 0 = 0, 3 · 0 = 0, то применим правило Лопиталя:
lim |
sin 2 |
= lim |
(sin 2 )′ |
lim |
2 cos 2 |
= |
2 cos 0 |
= |
2 |
. |
||||||
3 |
(3 )′ |
3 |
|
3 |
|
|
||||||||||
|
→ |
0 |
|
→ |
0 |
0 |
|
|
|
3 |
||||||
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 267.1 |
Назад Вперёд |
Решение задачи 267.1
Область определения данной функции ( ) = (−∞, +∞). Найдем производную
′ = ( 3 − 5 2 + 6 − 7)′ = 2 − 5 + 6. 3 2
Область определения производной ( ′) = (−∞, +∞). Приравняв производную к нулю
′ = 0 |
2 − 5 + 6 = 0, |
найдем критические точки
|
|
|
1 = 2, |
2 = 3. |
|
|
||||
Составим таблицу |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(−∞; 2) |
|
2 |
|
(2; 3) |
3 |
(3; +∞) |
|
|
|
|
|
|
−37 |
|
|
|
−25 |
|
|
|
′ |
+ |
|
0 |
|
− |
|
0 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
Значит, |
|
|
|
|
|
|
|
|
|
|
1 = 2 — точка максимума, max = −5 |
37 ; |
|
|
|
||||||
2 = 3 — точка минимума, min = −2 |
; |
|
|
|
||||||
функция возрастает при (−∞; 2], [3; +∞); |
||||||||||
функция убывает при [2; 3]. |
|
|
|
[Вернуться к условию] |
||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 268.1 |
Назад Вперёд |
Решение задачи 268.1
Область определения данной функции ( ) = (−∞, +∞). Найдем производную вторую производную
′ = ( 4 − 4 3 + − 1)′ = 4 3 − 12 2 + 1,
′′ = (4 3 − 12 2 + 1)′ = 12 2 − 24 .
Область определения второй производной ( ′′) = (−∞, +∞). Приравняв ′′ к нулю
|
|
|
′′ = 0 |
12 2 − 24 = 0, |
|||||
найдем точки |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
= 0, |
2 = 2. |
|
|||
Составим таблицу |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
(−∞; 0) |
|
0 |
|
(0; 2) |
2 |
(2; +∞) |
|
|
|
′′ |
|
|
−1 |
|
|
−15 |
|
|
|
|
|
|
|
|
|||
|
|
|
+ |
|
0 |
|
− |
0 |
+ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Значит, (0; −1), (2; −15) — точки перегиба;
функция выпукла (выпукла вверх) при [0; 2]; функция вогнута (выпукла вниз) при (−∞0], [2 + ∞).
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 269.1 |
Назад Вперёд |
Решение задачи 269.1
Функция = 3 − 3 непрерывна на отрезке [0; 2]. Найдем производную
′ = ( 3 − 3 )′ = 3 2 − 3.
Производная ′ непрерывна на отрезке [0; 2]. Приравняв производную к нулю
′ = 0 |
3 2 − 3 = 0, |
|
найдем критические точки |
|
|
1 = −1, |
2 = 1. |
|
Точка 1 = −1 ̸ [0; 2], а 2 = 1 [0; 2].
Вычислим значения функции в полученной точке и на концах отрезка:
(1) = −2, |
(0) = 0, |
(2) = 2. |
Значит, наибольшее значение функции
наиб = (2) = 2;
наименьшее значение функции
наим = (1) = −2.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 270.1 |
Назад Вперёд |
Решение задачи 270.1
Найдем вертикальные асимптоты.
Область определения функции ( ) = (∞; −1) (1; +∞). Поскольку
|
|
|
|
1 0 |
|
3 |
|
|
−∞ |
|
|
|
|
|
|
|
|
||
|
|
|
|
( + 1)2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
lim |
|
|
= |
|
|
, |
|
|
|
|
|
|
|
|||
|
|
|
→− ± |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то = −1 — вертикальная асимптота. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Найдем наклонные асимптоты = + . При → +∞ |
|
|
|||||||||||||||||
|
= |
lim |
( ) |
|
= lim |
|
|
|
3 |
|
|
= 1, |
|
|
|
|
|||
|
|
|
( + 1)2 |
|
|
|
|
||||||||||||
→+∞ |
− |
|
→+∞ |
→+∞ |
|
|
|
|
|
− |
|
||||||||
|
→+∞ ( |
( + 1)2 |
− |
|
) |
|
→+∞ −( + 1)2 |
|
|||||||||||
= lim ( ( ) |
|
) = lim |
3 |
|
|
|
= |
|
lim |
|
2 2 − 2 |
= |
|
2. |
|||||
|
|
|
|
|
|
|
|
|
|||||||||||
Значит, = − 2 — наклонная асимптота. |
|
|
|
|
|
|
|
|
→ −∞ прямая |
||||||||||
Аналогичным образом можно получить, что при |
|||||||||||||||||||
= − 2 также является наклонной асимптотой. |
|
[Вернуться к условию] |
|||||||||||||||||
Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 271.1 |
Назад Вперёд |
Решение задачи 271.1
Область определения ( ) = (−∞; +∞). Найдем пределы при , стремящимся к концам промежутков области определения
|
|
|
lim |
( ) = |
lim |
1 |
( |
3 |
+ 3 |
2 |
− 9 + 1) = +∞, |
|
||
|
|
4 |
|
|
|
|||||||||
|
+ |
∞ |
+ |
∞ |
|
|
|
|||||||
|
|
|
→ |
|
→ |
1 |
|
|
|
|
|
|
||
|
|
|
lim |
( ) = |
lim |
( 3 |
+ 3 2 |
− 9 + 1) = −∞. |
|
|||||
|
|
|
|
|||||||||||
|
4 |
|
||||||||||||
|
|
|
→−∞ |
|
→−∞ |
|
|
|
|
|
|
|
||
Так как ( ) = (−∞; +∞), то вертикальных асимптот нет. |
||||||||||||||
Функция не является ни четной, ни нечетной, т.к. |
+ 9 + 1). |
|||||||||||||
(− ) = 4((− )3 + 3(− )2 − 9(− ) + 1) |
= 4( − 3 + 3 2 |
|||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
Функция не является периодической.
Точки пересечения с осями координат. С осью : = 0. Получим уравнение
3 + 3 2 − 9 + 1 = 0.
Это уравнение достаточно сложное для решения, поэтому пропустим этот пункт.
С осью : = 0. Тогда
= 14(03 + 3 · 02 − 9 · 0 + 1) = 14.
Получили точку (0; 1).
Исследуем функцию на монотонность и экстремум. Найдем производ-
ную
′ = 14( 3 + 3 2 − 9 + 1)′ = 34 2 + 32 − 94.

Часть II. Задачи |
|
|
|
|
|
|
|
|
|
|
|
|
||
Решения и указания |
|
|
|
|
|
|
|
|
|
|
|
|||
Глава 3. Теория дифференцирования |
|
|
|
|
|
|
|
|
|
|||||
Меню Решение задачи 271.1 |
|
|
|
|
|
|
|
|
|
|
Назад Вперёд |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Область определения производной ( ′) = ( |
−∞ |
, + |
∞ |
). |
|
|||||||||
Приравняв производную к нулю |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
′ = 0 |
|
3 2 |
+ 6 |
− |
9 = 0, |
|
|
||||
найдем критические точки |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Составим таблицу |
1 = −3, |
2 = 1. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(−∞; −3) |
−3 |
(−3; 1) |
|
|
1 |
|
|
(1; +∞) |
|
||
|
|
|
|
7 |
|
|
|
−1 |
|
|
|
|
||
|
′ |
|
+ |
0 |
|
− |
|
|
0 |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значит,
1 = −3 — точка максимума, max = 7;
2 = 1 — точка минимума, min = −1;
функция возрастает при (−∞; −3], [1; +∞); функция убывает при [−3; 1].
Определим интервалы выпуклости и точки перегиба. Найдем вторую
производную |
|
1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
||||
|
′′ |
(3 2 + 6 − 9)′ = |
|
|
||||||||||||||||
|
= |
|
|
+ |
|
|
. |
|||||||||||||
4 |
2 |
2 |
||||||||||||||||||
Область определения ′′: ( ′′) = ( |
|
|
, + |
∞ |
). |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|||||
Приравняв вторую производную к нулю |
|
|
|
|
|
|||||||||||||||
|
|
|
′′ = 0 |
3 |
|
+ |
3 |
= 0, |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
2 |
|
|
|
|||||||||||||
найдем точку = −1. Составим таблицу |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
(−∞; −1) |
−1 |
(−1; +∞) |
||||||||||||||||
|
|
′′ |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
− |
|
|
0 |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
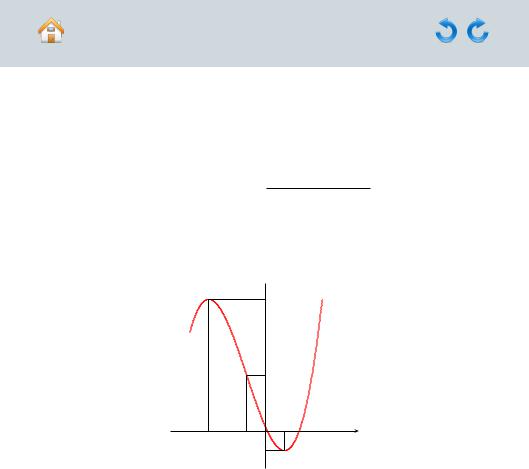
Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 271.1 |
Назад Вперёд |
Значит, (−1; 3) — точка перегиба;
функция выпукла при (−∞; −1]; функция вогнута при [−1 + ∞).
Найдем наклонные асимптоты = + . При → +∞
= |
lim |
( ) |
= |
|
lim |
3 + 3 2 − 9 + 1 |
= |
∞ |
. |
|||
|
|
|
||||||||||
|
+ |
∞ |
|
+ |
∞ |
|
|
|||||
|
→ |
|
|
|
→ |
|
|
|
|
|||
Значит, наклонных асимптот нет.
Множество значений функции ( ) = (−∞; +∞). Построим график.
y 
b7
b3
|
−1 |
1 |
|
b |
|
−3 |
O |
x |
−1 |
b |
|
|
|
|
|
Рисунок Р.14 |
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 272.1 |
Назад Вперёд |
Решение задачи 272.1
Доход, который можно получить, продав единиц продукции по цене ( ) равен ( ) = ( ). Поэтому функция прибыли будет иметь вид
Π( ) = ( ) − ( ) = ( ) − ( ) = |
|
|
|
|
|
|
|
|
− 10 2 |
− 800. |
||||||||||||||||||
|
|
= (50 − 10) − 50 |
|
− 15 − 800 = 50 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1749 |
|
1 |
|
|
|||||||
Исследуем функцию прибыли на максимальное значение при > 0. |
||||||||||||||||||||||||||||
Найдем производную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Π′( ) = ( |
1749 |
1 |
2 − 800) |
′ |
|
|
1749 |
|
|
1 |
|
|
|
|
|||||||||||||
|
|
|
− |
|
|
= |
|
|
− |
|
|
. |
|
|||||||||||||||
50 |
10 |
|
50 |
5 |
|
|||||||||||||||||||||||
Приравняем Π′( ) к нулю: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Π′( ) = 0 |
1749 |
− |
|
1 |
= 0. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
50 |
|
5 |
|
|
|
|
|
|
||||||||||||||||
Отсюда = 174, 9. Составим таблицу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
0 |
|
(0; 174, 9) |
|
|
174, 9 |
|
|
|
(174, 9; +∞) |
|
|
||||||||||||||
|
Π |
|
−800 |
|
|
|
|
|
2259, 001 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Π′ |
|
|
|
|
|
+ |
|
|
|
|
0 |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Значит, прибыль максимальна при продаже max = 174, 9 единиц продукции и составляет Πmax = 2259, 001.
Отметим, что если по смыслу задачи — целое, то для нахождения решения задачи дополнительно нужно вычислить значение функции Π( ) в ближайших к полученному max целых числах. В нашем случае
Π(174) = 2258, 92; Π(175) = 2259.

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 272.1 |
Назад Вперёд |
Поэтому при условии целочисленности , прибыль максимальна при продажеmax = 175 единиц продукции и составляет Πmax = 2259.
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 273.1 |
Назад Вперёд |
Решение задачи 273.1
b
b
ϕ |
|
b |
b |
Рисунок Р.15 |
|
Обозначим через — точку железной дороги, ближайшую к , — точку между и , где подъездной путь будет пересекать железную до-
рогу (см. рисунок |
Р.15). Пусть = , тогда по теореме Пифагора |
|||
= √ |
|
= √ |
|
— длина подъездного пути к железной до- |
2 + 2 |
64 + 2 |
|||
роге. Кроме того, = − = 15 − — длина пути по железной дороге. Учитывая стоимость провоза груза по подъездному пути и по железной дороге, найдем общую стоимость транспортировки:
√
= ( ) = · + · = 4 64 + 2 + 2(15 − ).
По смыслу задачи [0; 15]. Исследуем функцию ( ) на наименьшее зна-
чение на этом отрезке. Найдем производную |
|
= √64 + 2 − 2. |
||||||||||||
′( ) = (4√64 + 2 + 2(15 − ))′ |
||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
||||
Приравняв производную к нулю, найдем критические точки: |
||||||||||||||
|
|
|
|
|
|
|
8√ |
|
|
|
||||
′( ) = 0 |
√ |
4 |
|
|
|
3 |
|
|||||||
|
− 2 = 0 |
|
= |
|
|
[0; 15]. |
||||||||
3 |
||||||||||||||
64 + 42 |
||||||||||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 273.1 |
Назад Вперёд |
Найдем значения функции ( ) в найденной точке и на концах отрезка [0; 15]:
( |
|
√ |
|
|
|
) ≈ 57, 7; |
|
|
|
|
|
|
|
|
|
||
8 |
|
3 |
(0) = 62; |
|
(15) = 68. |
||||||||||||
|
3 |
|
|
|
|||||||||||||
Значит, наим = ( |
|
√ |
|
) ≈ 57, 7, а для нахождения угла поступим так: |
|||||||||||||
8 |
|
|
3 |
||||||||||||||
|
3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
8 |
|
|
|
√ |
|
|
||
|
|
|
|
|
|
|
tg = |
|
= |
|
8√ |
|
|
= 3. |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
3 |
||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
Поэтому, = . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию] |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Часть II. Задачи |
|
Решения и указания |
|
Глава 3. Теория дифференцирования |
|
Меню Решение задачи 274.1 |
Назад Вперёд |
Решение задачи 274.1
Пусть млрд. руб. инвестируется в производство, тогда 1 − млрд. руб. размещается в банк. Размещенный в банк капитал через год будет равен
б( ) = (1 − ) |
(1 + 100) |
= (1 − ) (1 + |
100) |
= |
2 |
− 2 |
, |
||
|
|
1 |
|
50 |
|
|
3 |
3 |
|
а капитал, вложенный в производство
пр( ) = |
(1 + 100) |
= (1 + |
100) |
= 2 . |
|
|
|
2 |
|
100 |
|
По условию задачи издержки составят ( ) = 2 = 3 2, т.е. прибыль от вложения в производство Π1( ) = ( ) − ( ) = 2 − 3 2. Налоги составят
( ) = Π1( )1003 = (2 − 3 2) · 0, 1.
Таким образом, чистая прибыль от вложения средств в производство составит
Πпр( ) = Π1( ) − ( ) = 2 − 3 2 − (2 − 3 2) · 0, 1 = 0, 9(2 − 3 2).
Значит суммарная прибыль составит
Π( ) = б( ) + Πпр( ) = 32 − 32 + 0, 9(2 − 3 2) = 0, 3 − 2, 7 2 + 1, 5.
Исследуем функцию Π( ) на наибольшее значение при [0; 1]. Найдем производную
Π′( ) = (0, 3 − 2, 7 2 + 1, 5)′ = 0, 3 − 5, 4 .

Часть II. Задачи |
|
|
|
|
|
Решения и указания |
|
|
|
|
|
Глава 3. Теория дифференцирования |
|
|
|
|
|
Меню Решение задачи 274.1 |
|
|
|
|
Назад Вперёд |
|
|
||||
Приравняв производную к нулю, отыщем критические точки |
|||||
Π′( ) = 0 |
0, 3 − 5, 4 = 0 |
|
1 = |
1 |
. |
|
|||||
18 |
|||||
Найденная точка принадлежит отрезку исследования. Осталось вычислить значения данной функции в критических точках и на концах отрезка
|
|
Π ( |
|
Π(0) = 1, 5; |
|
|
|
|||
|
|
18) = 120 ≈ 1, 508; |
|
|||||||
|
|
|
1 |
|
181 |
|
|
|
|
|
|
|
Π(1) = |
0, 3 − 2, 7 + 1, 5 = −0, 9. |
|
||||||
Значит, наибольшее значение функции Πнаиб = Π |
1 |
= 120181 . Таким обра- |
||||||||
18 |
||||||||||
зом, для получения максимальной прибыли в |
производство следует вложить |
|||||||||
( |
) |
|||||||||
1 = |
1 |
млрд. рублей, а в банк — 2 |
= 17 млрд. рублей. |
|||||||
18 |
||||||||||
|
|
|
|
18 |
|
|
|
|
||
[Вернуться к условию]

Часть II. Задачи Решения и указания
Глава 4. Теория интегрирования
Меню |
Назад Вперёд |
Глава 4. Теория интегрирования

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 302.1 |
Назад Вперёд |
Решение задачи 302.1
Воспользуемся формулой возведения в квадрат, свойством линейности неопределенного интеграла и таблицей интегралов:
∫ |
(2 + 1)2 = ∫ |
(4 2 + 4 + 1) = ∫ |
4 2 + ∫ |
4 + ∫ |
= |
|||||||
= 4 |
∫ |
2 + 4 ∫ |
+ ∫ |
= 4 |
3 |
+ 4 |
2 |
+ + = |
3 3 + 2 2 + + . |
|||
|
|
|
|
|
|
3 |
|
2 |
4 |
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 303.1 |
Назад Вперёд |
Решение задачи 303.1
Выполнив замену 3 = , сведем интеграл к табличному: |
|
|
|||||||||||||
∫ |
|
3 = |
1 |
|
|
|
∫ |
3 |
|
|
|
|
|||
cos 3 = |
|
|
3 |
|
|
= |
|
cos 1 = |
|
|
|
|
|||
|
3 = , |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
= |
|
∫ |
cos = |
|
sin + = |
|
sin 3 + . |
|||
|
|
|
|
3 |
3 |
3 |
|||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 303.2 |
Назад Вперёд |
Решение задачи 303.2
Выполнив замену sin 5 = , сведем интеграл к табличному: |
|
||||||||||||||||||||||||||
∫ |
√sin3 5 |
|
|
sin 5 = , |
1 |
|
|
|
|
∫ |
√ 3 5 |
5 |
∫ |
|
|||||||||||||
|
cos 5 |
= |
|
5 cos 5 = , |
|
= |
|
1 |
|
|
1 |
= |
1 |
|
− 23 = |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
5 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 5 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 − 2 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
= |
|
|
|
+ = − |
5√ |
|
|
+ = − |
5√ |
|
+ . |
|||||||||||
|
|
|
|
|
5 |
−21 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
sin 5 |
|||||||||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 303.3 |
Назад Вперёд |
Решение задачи 303.3
Выполнив замену ctg 4 = , сведем интеграл к табличному:
|
√ |
|
|
|
|
|
ctg 4 = , |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||
|
ctg 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
= |
|
|
4 |
|
|
|
|
= , |
= |
|
√ |
− |
= |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2 |
|
|
|
|
2 |
4 |
|
|
4 |
||||||||||||||||||||||||||
∫ |
sin |
4 |
|
|
|
−sin |
|
|
|
|
1 |
|
|
|
∫ |
|
|
|
|
( |
) |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
sin 4 |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
= − |
|
∫ |
2 |
= − |
|
|
|
|
+ = − |
|
√ 3 + |
= − |
|
√ctg3 4 + . |
|||||||||||||||||||
|
|
|
4 |
4 |
23 |
6 |
6 |
|||||||||||||||||||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 303.4 |
Назад Вперёд |
Решение задачи 303.4
Выполнив замену arctg = , сведем интеграл к табличному:
∫ |
|
|
|
1+ |
||
|
|
|
|
arctg = , |
||
(1 + 2)√arctg |
= |
|
|
1 2 = |
||
|
|
|||||
|
|
|
|
|
|
|
∫ 1
= √ =
√
= 2 + = 2 arctg + .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 303.5 |
Назад Вперёд |
Решение задачи 303.5
Выполнив замену 5 − 2 2 = , сведем интеграл к табличному:
2 |
|
5 − 2 2 = , |
|
∫ (− |
1 |
|
) |
|
|
|
|
|
|
|
|||||
∫ |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
4 |
|
|
|
|
|
|
|
||||||||
5−2 = |
|
|
|
|
4 |
|
|
= |
|
|
|
= |
|
|
|
|
|
||
|
|
4 = , |
|
|
|
|
|
|
|
|
|
||||||||
|
|
= |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
5 |
|
2 2 |
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
+ = − |
|
|
− |
|
+ . |
|
|
|
|
|
|
|
4 |
|
4 |
|
||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 303.6 |
Назад Вперёд |
Решение задачи 303.6
Разобъем интеграл на два |
∫ |
|
|
− ∫ |
|
|
|
||
∫ |
2 + 16 |
2 + 16 |
|
2 + 16 |
|
||||
|
2 − 4 |
= |
|
2 |
|
|
4 |
|
. |
|
|
|
|
|
|
|
|||
Второй интеграл в правой части является табличным:
∫
41
2 + 16 = 4 · 4 arctg 4 + = arctg 4 + .
Впервом интеграле выполним замену 2 + 16 = :
∫ |
2 + 16 |
= |
|
2 = |
|
= ∫ |
|
= ln | | + = ln( 2 + 16) + . |
||
|
2 |
|
|
2 + 16 = , |
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончательно получим |
|
|
|
|
|
|||||
∫ |
2 + 16 |
|
− |
|
4 |
|
|
|
2 − 4 |
|
= ln( 2 + 16) |
|
arctg |
|
+ . |
|
|
|
|
||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 304.1 |
Назад Вперёд |
Решение задачи 304.1
Воспользуемся формулой интегрирования по частям. Получим
∫ |
|
|
= ln( + 8), |
|
|
|
|
|
|
|
|
|
|||||
|
= +8 , |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
= , |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln( + 8) |
= |
|
|
1 |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
− ∫ |
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
+ 8 |
|
|
|
|
− |
+ 8 |
8 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
+ 8 |
|
|
||||
= ln( + 8) |
|
|
|
|
|
|
= ln( + 8) |
|
|
|
|
− |
|
= |
|||
|
|
|
|
|
|
|
+ 8 = |
|
|||||||||
|
= ln( + 8) − ∫ |
+ 8 + ∫ |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
+ 8 |
|
|
8 |
|
|
|
|
||
= ln( + 8) − + 8 ln | + 8| + = ( + 8) ln( + 8) − + .
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 304.2 |
Назад Вперёд |
Решение задачи 304.2
Воспользуемся формулой интегрирования по частям ∫ |
= − ∫ |
: |
||||||||||||||||||||||||||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
|
= ln , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
− |
|
|
|
|
|
|
|
|
= , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
+ 1) |
, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
= ( 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
( |
|
|
+ 1) ln = |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
− |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
· |
( |
3 |
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
− |
2 |
|
|
) − ∫ |
( |
3 − 2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
|
1 |
|
|
|
||||
|
|
|
= ln |
|
|
|
|
|
|
2 |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
= |
|
|||
|
|
|
|
|
3 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
= |
( |
|
|
|
|
|
+ )ln − ∫ ( 3 |
− 2 + 1) |
= |
|
|
||||||||||||||||||||
|
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
( 3 2 ) 3 2
= 3 − 2 + ln − 9 + 4 − + .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 304.3 |
Назад Вперёд |
Решение задачи 304.3
|
|
|
|
|
|
|
|
|
|
|
|
интегрирования по частям |
∫ |
= |
|
: |
|||||||||||||||||||||||||||||||||||||||
Воспользуемся формулой |
|
|
|
|
|
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
∫ |
||||||||||||||||||||
|
∫ |
|
|
|
|
|
|
|
= ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
− |
|
|
|
= |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
= (3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
(3 |
|
|
2) ln = |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 ln − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= 2 |
|
|
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
= ln2 · ( |
|
|
|
|
|
|
|
|
|
|
( |
2 |
|
− 2 ) |
|
|
|
|
= |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
− 2 ) − ∫ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
2 ln |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
2 |
|
− 2 )ln2 − 2 ∫ |
(32 − 2)ln . |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Последний интеграл также возмем по частям: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= ln , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∫ ( |
|
− ) |
|
|
|
|
|
|
|
|
|
( , |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
= |
|
2 |
|
|
|
|
|
|
2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
32 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
2 ln = |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
4 |
|
|
|
− |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
· ( |
|
|
|
|
|
|
|
) |
|
|
( |
4 |
|
− |
) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
− |
|
|
|
|
|
|
− ∫ |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
= ln |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
= |
|
|
|
|
|
||||||||||
|
(34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= |
|
− 2 )ln − ∫ ( |
|
4 − 2) = ( |
4 |
|
|
− 2 )ln − 8 |
+ 2 + . |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
||||||||
Окончательно получим |
|
|
|
|
|
|
|
− 2 )ln2 − ( |
|
|
|
|
|
− 4 )ln + 34 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
∫ |
(3 − 2) ln2 = ( |
2 |
|
2 |
|
|
|
|
+ 4 + . |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 304.4 |
Назад Вперёд |
Решение задачи 304.4
Воспользуемся |
|
формулой |
интегрирования |
|
по частям. |
|
Положим |
||||||||||||||||||||||||||||||||||||||||
= arcsin 2 , = |
√ |
|
|
|
|
|
. Тогда = |
√ |
2 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2 |
|
1−4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1−4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
√1 4 2 |
|
− |
|
|
|
|
|
|
|
|
|
|
|
−8 |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− 4 2 = |
, |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
= |
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
8 |
, |
|
= |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
8 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
4 |
√ |
+ = |
− |
4 |
√ |
1 |
− |
4 + . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Поэтому, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫ √1 − 4 2 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
arcsin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= arcsin 2 · |
(−4 |
|
1 − 4 2) − ∫ (−4 |
|
|
|
1 − 4 2) √1 |
2 |
|
4 2 |
|
= |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
√ |
|
|
|
∫ |
|
|
|
1 |
√ |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
= −4 |
√1 − 4 2 arcsin 2 + 2 |
= −4 |
|
|
|
|
|
2 + . |
|||||||||||||||||||||||||||||||||||||||
√1 − 4 2 arcsin 2 + |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 304.5 |
Назад Вперёд |
Решение задачи 304.5
Воспользуемся формулой интегрирования по частям. В этом случае
∫ |
|
|
|
|
|
= + 8, |
|
|
|
|
|
|
||||
|
|
|
|
= , |
|
|
|
|
|
|||||||
|
|
|
|
|
|
= sin 3 , |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( + 8) sin 3 = |
|
|
|
|
|
1 |
|
= |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
1 |
|
− |
|
|
1 |
|
1 |
|
||
|
|
|
|
|
= |
|
3 cos 3 |
|
|
|
||||||
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
|
|
3 |
∫ |
|
|
−3 |
|
9 |
|
||||
= |
|
|
( |
+ 8) cos 3 |
+ |
|
|
|
cos 3 = |
|
|
( + 8) cos 3 + |
|
sin 3 + . |
||
|
|
|
|
|
|
|
|
|||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 304.6 |
Назад Вперёд |
Решение задачи 304.6
Воспользуемся формулой интегрирования по частям дважды. Имеем
∫ |
|
|
− |
|
|
= 2 − 3, |
|
|
|
|
|
= 2 , |
|
||||
|
|
2 |
|
|
|
= cos , |
|
|
|
|
|
|
|
|
|
||
|
( |
|
|
3) cos = |
|
|
|
= |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= , |
|
|
|
|
|
|
= sin |
|
|
|
|
|
|
|
|
|
|
|
|
− |
− |
∫ |
|
|
|
= , |
|
|
|
|||
|
2 |
|
|
|
|
|
|
= sin , |
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
= ( |
|
|
3) sin |
2 |
sin = |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
− |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
cos |
|
|
|
|
= ( 2 − 3) sin − 2 |
(− cos + |
∫ |
cos ) |
= |
|
|||||||||
= ( 2 − 3) sin − 2(− cos + sin ) + = ( 2 |
− 5) sin |
+ 2 cos + . |
||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 304.7 |
Назад Вперёд |
Решение задачи 304.7
Воспользуемся формулой интегрирования по частям. В этом случае
∫ |
− |
|
|
|
|
= , |
|
|
|
|
|
|
|
|
|
|
|
|
= , |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
= cos( |
|
4) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||
cos( |
|
4) = |
|
|
|
|
|
= |
|
|
|
|
|||
|
|
|
− |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= sin( |
|
4) |
|
|
|
|
|
|
|
= sin( |
− |
4) |
− ∫ |
− |
4) = |
sin( |
− |
4) + cos( |
− |
4) + . |
|||||
|
sin( |
|
|
|
|||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 305.1 |
Назад Вперёд |
Решение задачи 305.1
Выпишем знаменатель и выделим в нем полный квадрат:
|
|
|
|
|
|
|
2 + 2 + 2 = ( + 1)2 + 1. |
|
|
|
|
||||||||||||
Подставим в исходный интеграл и сделаем замену: |
|
∫ |
|
|
|||||||||||||||||||
∫ |
( + 1)2 + 1 |
|
|
|
= |
|
|
|
∫ |
2 + 1 |
|
2 + 1 |
|||||||||||
|
2 − 3 |
= |
|
+ 1 = , |
|
= |
|
|
2( − 1) − 3 = |
|
2 − 5 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее разобъем подынтегральную |
дробь |
на две и воспользуемся известными |
|||||||||||||||||||||
методами: |
∫ |
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
||||
∫ |
2 + 1 |
2 |
+ 1 |
|
− |
|
|
2 + 1 |
|
|
− |
|
|
|
|||||||||
|
2 − 5 |
= |
|
2 |
|
|
|
5 |
|
|
|
|
1 |
|
|
= ln( 2 + 1) |
|
5 arctg + = |
|||||
|
|
|
|
|
|
|
|
|
= ln( 2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 2 + 2) − 5 arctg( + 1) + . |
||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 305.2 |
Назад Вперёд |
Решение задачи 305.2
Так как степень числителя подынтегральной функции равна степени знаменателя, то, разделив числитель на знаменатель, получим
|
|
|
3 + 2 2 + 2 + 3 |
= 1 + |
|
|
3 2 − + 6 |
. |
|
|||
Значит, |
|
|
3 − 2 + 3 − 3 |
|
|
3 − 2 + 3 − 3 |
||||||
|
|
|
|
|
|
|||||||
|
|
− 2 |
+ 3 − 3 = + |
∫ |
3 − 2−+ 3 − 3 . |
|||||||
∫ |
3 |
|
||||||||||
|
3 |
+ 2 2 |
+ 2 + 3 |
|
|
|
3 2 |
+ 6 |
|
|
||
Для вычисления интеграла в правой части, вначале разложим на множители знаменатель:
3 − 2 + 3 − 3 = 2( − 1) + 3( − 1) = ( 2 + 3)( − 1).
Теперь разложим подынтегральную дробь на простейшие дроби, воспользовавшись методом неопределенных коэффициентов. Имеем,
3 2 − + 6 |
= |
+ |
+ |
|
= |
|
|
|
|
( 2 + 3)( − 1) |
|
2 + 3 |
− 1 |
|
2 − + − + 2 + 3 |
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|
( 2 + 3)( − 1) |
|
Приравнивая коэффициенты при одинаковых степенях в конечном и начальном числителе, получим систему
+ = 3,
− + = −1,
− + 3 = 6,

|
Часть II. Задачи |
|
|
|
|
|
|
|
|
|
|
|
||
|
Решения и указания |
|
|
|
|
|
|
|
|
|
||||
|
Глава 4. Теория интегрирования |
|
|
|
|
|
|
|||||||
Меню |
Решение задачи 305.2 |
|
|
|
|
|
|
|
|
Назад Вперёд |
||||
|
|
|
|
|
|
|
|
|
|
|
||||
решая которую, найдем |
|
|
= 1, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2. |
|
|
|
|
||
Возвращаясь к вычислению |
интеграла, будем иметь |
|
||||||||||||
|
|
|
∫ |
|
|
|
|
|||||||
∫ |
( 2 + 3)( − 1) |
|
∫ |
2 + 3 |
|
− 1 |
|
|
||||||
|
3 2 |
− + 6 |
|
|
= |
|
|
+ |
2 |
= |
|
|||
|
|
|
|
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
= |
ln( 2 + 3) + 2 ln |
| − 1| + . |
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|||||
Окончательно, |
+ 3 − 3 |
= + 2 ln( 2 + 3) + 2 ln | − 1| + . |
||||||||||||
|
∫ |
3 |
− 2 |
|||||||||||
|
|
3 |
+ 2 2 |
+ 2 + 3 |
|
|
1 |
|
|
|
|
|
||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 306.1 |
Назад Вперёд |
Решение задачи 306.1
Сделаем замену: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
√4 |
|
= , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∫ |
√2 |
|
1 |
|
√2 |
|
1 |
|
|
2 − 1 |
|
∫ |
|
|
|
|
|
∫ |
|
|
|
1 |
|
||||||||
− |
− |
− |
|
= 2 ( 4 |
− |
1), |
|
− |
− |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 = 4, |
|
|
2 3 |
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
= |
|
|
|
−1 |
|
|
|
|
|
= |
|
2 |
|
|
|
= 2 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Получили интеграл от рациональной функции. Для вычисления отнимем и добавим в числителе единицу, разобъем интеграл на сумму интегралов и воспользуемся таблицей интегралов:
∫ |
− 1 |
∫ |
− 1 |
∫ ( |
− 1) |
|||
2 |
2 |
= 2 |
2 |
− 1 + 1 |
= 2 |
+ 1 + |
1 |
= |
|
|
|
|
|||||
( 2 )
= 2 2 + + ln | − 1| + =
= √2 − 1 + 2√4 2 − 1 + ln (√4 2 − 1 − 1)2 + .
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 306.2 |
Назад Вперёд |
Решение задачи 306.2
Сделаем замену: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∫ |
√ + 2 |
|
|
|
|
|
|
|
− |
|
|
|
∫ |
|
|
|
|
|
· − |
|
|
|
|
||||||||||
|
− 1 = |
|
|
√ |
|
+ 2 = , |
|
= |
( − 2)2 − 1 |
|
2( |
2) = |
|||||||||||||||||||||
|
|
= ( 2)2, |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
= 2 |
|
|
3 |
− |
|
|
2 |
|
|
− |
|
. |
|
|
|
|
|
|
|
|
|
|
|
= 2( |
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
6 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 11 |
|
|
||||||
Разобъем на сумму интегралов: |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|||||||||||||||||
2 ∫ |
|
|
|
− |
|
|
|
|
|
− |
|
= 2 ∫ ( |
|
− 6 |
|
+ 11 − 6 |
= |
|
|
|
|||||||||||||
|
3 |
|
6 2 |
+ 11 |
|
|
6 |
|
|
|
3 |
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
= 2 ∫ |
2 − 12 ∫ |
+ 22 ∫ |
|
− 12 |
= |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
=23 3 − 6 2 + 22 − 12 ln | | + =
=23(√ + 2)3 − 6(√ + 2)2 + 22(√ + 2) − 12 ln(√ + 2) + =
=23√ 3 − 2 + 6√ − 12 ln(√ + 2) + .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 307.1 |
Назад Вперёд |
Решение задачи 307.1
Для |
вычисления |
|
интеграла |
применим |
|
формулу |
|||||
sin cos = 1 |
(sin( + ) + sin( + )). Тогда |
|
|
|
|
||||||
∫ |
2 |
|
|
|
∫ |
(sin 5 − sin ) = |
|
|
|
|
|
sin 2 cos 3 = 2 |
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
= 2 |
∫ sin 5 − 2 |
∫ sin = −10 cos 5 + |
2 cos + . |
||||||
|
|
1 |
|
|
|
1 |
|
1 |
|
1 |
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 307.2 |
Назад Вперёд |
Решение задачи 307.2
Произведем замену: |
|
|
|
∫ |
sin2 cos = |
|
sin = , |
cos = |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫ |
2 = 3 |
+ = 3 sin3 + . |
|||
|
|
3 |
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию] |
||

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 307.24 |
Назад Вперёд |
Решение задачи 307.24
При помощи универсальной тригонометрической подстановки сведем данную задачу к интегрированию рациональной функции. Имеем,
∫ |
|
|
|
tg |
|
= , |
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
= |
|
|
|
1+ |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= |
|
2 |
|
|
1 2 |
|
|
= |
|
|
|
1 |
|
|
|
|
2 |
|
= 2 |
|
|
2 . |
|||||||||
|
|
cos |
= |
1+− 2 |
, |
|
|
|
1 |
|
2 |
|
|
|
2 |
|
|
||||||||||||||||
2 + cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + − |
2 |
|
1 + |
|
|
|
3 + |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вычисляя последний |
интеграл с помощью |
таблицы интегралов, |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
∫ |
|
3 + 2 = |
√3 arctg |
√3 |
+ , |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и производя обратную замену, окончательно получим |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
∫ |
|
|
= |
|
arctg ( |
3 |
tg |
|
|
) + . |
|
|
|
|
|||||||||||||||||
|
|
|
2 + cos |
|
3 |
|
3 |
2 |
|
|
|
|
|||||||||||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 308.1 |
Назад Вперёд |
Решение задачи 308.1
Воспользуемся свойством линейности определенного интеграла и применим формулу Ньютона–Лейбница:
∫ |
(6 2 |
− 5) = 6 |
∫ |
2 − 5 |
∫ |
= 6 33 0 − 5 0 = |
||||||||
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
2 |
|
2 |
0 |
|
|
0 |
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
= 6 |
( |
|
− 0) − 5(2 − 0) = 16 − 10 = 6. |
||||||
|
|
|
|
|
3 |
|||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.1 |
Назад Вперёд |
Решение задачи 309.1
Вычислим этот интеграл, произведя подходящую замену. При этом дополнительно следует проконтролировать, как изменятся границы интегрирования. Именно,
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
= , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 = , |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
0 |
|
|
− |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|||||||||
0 |
2 |
|
|
|
= |
|
, |
|
0 |
1 |
|
1 |
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
= |
|
1 |
|
1 |
2 |
|
|
= |
|
|
= |
|
|
|
= ( 1). |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию] |
|||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.2 |
Назад Вперёд |
Решение задачи 309.2
Выполним замену ln = . Получим
|
|
|
|
ln = , |
|
|
||
|
|
|
1 = , |
|
||||
|
|
|
|
|
1 |
|||
∫ |
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
1 |
|
|||||
1 |
sin(ln ) |
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
|
|||||
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
sin = − cos |
|
|
= |
0 |
|||
|
|
|
|
= − cos 1 + cos 0 = 1 − cos 1.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.3 |
Назад Вперёд |
Решение задачи 309.3
Воспользуемся свойством четности подынтегральной функции. Имеем
|
|
|
|
1 |
|
(1 2)√1 |
|
|
2 |
= 2 |
∫ |
1 |
(1 2)√1 |
|
|
2 . |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
∫1 |
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2 |
|
|
− |
|
|
|
|
|
|
− |
|
|
|
|
|
0 |
|
|
|
− |
|
|
− |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь выполним замену = sin . Получим |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= sin |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
2 |
√ |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
(1 |
) 1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
2 |
− |
|
|
− |
|
|
|
|
|
|
|
= cos , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
6 |
(1 |
|
|
sin2 |
) |
|
1 |
|
sin2 |
= |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
− |
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
= 2 |
∫ |
|
cos2 = 2 tg 0 |
= 2 |
tg 6 − tg 0 |
= |
3 . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
2√3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.4 |
Назад Вперёд |
Решение задачи 309.4
√
Выполним замену 4 + sin = . Получим
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|||
|
|
|
|
= |
|
4 + √sin = , |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|||
|
|
|
|
sin = ( 4)2 |
, |
|
|
||||||||
∫ |
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 + sin |
|
|
|
|
|
|
|
|
|
||||||
0 |
|
cos |
|
|
|
|
|
|
|
|
|
|
4) , |
||
|
|
|
|
cos = 2( |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
∫ |
− 4 ∫ |
|
|
|
|||||
|
|
|
|
= 2 |
|
|
= 2 |
||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
5 |
|
− |
|
|
= |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
4 |
|
2( |
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
5 |
|
|
|
|
4 |
− 4 ln | | 4) |
= 2 − 8 ln |
|
|||||||
( |
4. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.5 |
Назад Вперёд |
Решение задачи 309.5
Преобразуем подынтегральную функцию следующим образом:
∫3 |
2 + 3 + 4 |
|
∫3 |
2 + 3 + 4 |
|
|
|
|
|
|||
2 |
( − 1)2 |
|
|
2 |
2 − 2 + 1 |
|
|
|
|
|
|
|
− 2 |
|
= |
− 2 |
= |
|
|
|
|
|
|||
∫3 |
|
|
∫3 |
− |
∫3 |
2 + 3 + 4 |
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
2 + 3 + 4 |
|
||||||||
|
2 |
( 2 + 3 + 4) − (5 + 3) |
|
2 |
|
2 |
5 + 3 |
|
||||
|
= |
= |
|
|
|
. |
||||||
|
|
|
|
|
||||||||
|
− 2 |
|
|
|
|
|
|
− 2 |
|
− 2 |
|
|
Первый из полученных интегралов вычисляется элементарно:
∫ |
= 2 + 2 |
= 2. |
2 |
3 |
7 |
−32
Взнаменателе подынтегральной функции второго интеграла выделим полный квадрат:
2 + 3 + 4 = 2 + 2 · · 2 |
+ 4 |
− 4 + 4 = ( + |
2) |
2 |
+ 4. |
|
3 |
9 |
9 |
|
3 |
7 |
|
Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.5 |
Назад Вперёд |
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 3 |
= , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
5 + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
∫3 |
|
|
|
|
|
|
|
3 |
|
2 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
+ |
2 |
|
|
|
+ 4 |
|
|
|
|
|
|
|
|
|
|
2 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
− |
2 |
|
( |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
5 |
|
− |
+ 3 |
|
|
|
|
|
|
|
5 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
= |
|
|
|
|
2 |
= |
|
|
|
|
|
2 |
|
|
|
= 5 |
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
( |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|||||||||||||||||||||||||||||
|
|
∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫0 |
|
|
|
|
|
|
2 ∫0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 +)4 |
|
|
|
|
|
|
|
|
|
|
|
2 |
+ |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + |
4 − |
|
|
2 + |
4 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
2 |
|
2 + |
7 |
|
|
9 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
= |
|
|
|
∫ |
|
|
|
(2 + 474 ) |
|
− |
|
· |
|
|
√ |
|
arctg |
√ |
|
|
|
0 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
7 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
5 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
2 |
9 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 ln ( 2 + |
4)0 |
− √7 arctg √7 |
0 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9√ |
|
|
|
|
|
|
|||||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
7 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= |
|
|
|
|
|
ln 14 |
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
(arctg √7 |
|
|
|
|
arctg 0) = |
|
|
ln 8 |
|
|
|
|
|
|
|
|
|
arctg √7. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
( |
|
|
|
− |
|
|
|
4) − √7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
2 |
|
|
− |
|
7 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
Окончательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∫3 |
2 + 3 + 4 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
( − 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9√ |
|
arctg √ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− 2 |
|
|
|
= |
7 |
|
|
|
|
|
|
|
|
15 |
ln 2 + |
7 |
7 |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.6 |
Назад Вперёд |
Решение задачи 309.6
Воспользуемся методом интегрирования рациональных функций. Для этого разложим знаменатель на множители. Получим
3 − 1 = ( − 1)( 2 + + 1).
Разобъем подынтегральную дробь на простейшие. Имеем
|
= |
|
+ |
+ |
= |
|
|
|
|||
( − 1)( 2 + + 1) |
− 1 |
2 + + 1 |
= 2 + + + 2 + − − .
( − 1)( 2 + + 1)
Приравнивая коэффициенты в последнем и первом числителе, составим и решим систему:
+ = 0, |
|
= − , |
|
|
= |
31 ,1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
− + = 1, |
|
= , |
|
|
|
= −3 |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− = 0; |
|
+ + = 1; |
= |
3 . |
|
|||||||||
Таким образом, |
исходный интеграл равен |
∫ |
|
|
|
|
|
|||||||
|
∫ 3 − 1 3 |
∫ |
|
− 1 − |
3 |
2 |
+ + 1 |
|
|
|
||||
|
0 |
|
|
1 |
0 |
|
1 |
0 |
|
− 1 |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
. |
|
|
−1 |
−1 |
|
−1 |
|
|
|
|
|
||||||
Вычислим каждый из интегралов в правой части последнего равенства. Имеем
∫0 |
|
|
|
= ln | − 1| 0 |
1 = ln 1 − ln 2 = − ln 2, |
|
|
− |
1 |
||||
− |
1 |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.6 |
Назад Вперёд |
∫0
−1
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
+ |
1 |
= , |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
+ + 1 |
|
|
|
|
|
+ |
1 |
|
2 |
+ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
= |
|
1 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||||
|
|
|
− |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
= |
|
|
( |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
= |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
− |
|
|
|
− |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
2 |
+ |
43 |
|
|
|
2 |
|
|
2 + 43 |
|
|
2 |
|
|
|
43 |
|
|
|
|
|
|
|
|||||||||||
|
|
∫1 |
|
|
|
∫1 |
|
|
− 2 ∫1 |
2 + |
|
|
|
|
|
|
|
|||||||||||||||||||||
= |
|
|
|
|
− |
23 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
= |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
− 2 |
|
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 − 3 · √ |
|
|
arctg √ |
|
|
0 |
= |
−2√3 arctg 1√3 = −2√3 · |
6 |
|||||||||||||||||||||||||||||
3 |
3 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√
= − 3 3.
Заметим, что при вычислении использовалось свойство четности подынтегральной функции. Окончательно,
∫ |
3 − 1 = |
3 (− ln 2 + |
3 |
|
) = |
9 3 − 3 ln 2. |
||||||
0 |
|
|
|
|
√ |
|
|
√ |
|
|
|
|
|
|
1 |
3 |
|
1 |
|||||||
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.7 |
Назад Вперёд |
Решение задачи 309.7
Воспользуемся формулой понижения степени для тригонометрических функций. Имеем
∫0 |
|
|
|
|
|
|
(1 − |
|
2 |
|
|
|
) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
sin6 |
= ∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|
cos 2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
8 |
|
∫ |
|
|
|
− |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
− ∫ |
|
|
|
|
. |
|||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||
|
|
= |
1 |
|
|
|
|
|
3 |
|
cos 2 + 3 |
cos2 |
2 |
|
|
cos3 2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вычислим каждый из полученных интегралов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫0 |
|
|
|
|
2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∫ |
|
cos 2 = |
2 sin 2 0 |
= |
|
2(sin − sin 0) = 0, |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
( + 4 sin 4 )0 |
= |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
cos2 2 = 2 |
(1 + cos 4 ) = |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
0 |
2 |
|
|
|
|
|
1 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
( |
2 |
+ |
|
4 sin 2 ) |
− 2 |
(0 + 4 sin 0) |
= |
4 , |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
Часть II. Задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решения и указания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Глава 4. Теория интегрирования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Меню |
Решение задачи 309.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Назад Вперёд |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫0 |
|
|
cos2 |
2 · cos 2 = |
2 |
∫0 |
|
|
|
|
|
|
|
|
|
|||||||
cos3 2 = |
∫0 |
(1 − sin2 2 ) (sin 2 ) = |
|
|||||||||||||||||||
|
2 |
2 |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
(sin 2 − |
|
3 |
|
)0 |
= 0. |
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
sin |
3 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончательно получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∫ |
|
|
|
|
|
2 − 0 + 3 · 4 |
− 0 = |
32 . |
|
|
|
|
|
||||||||
|
sin6 = 8 |
( |
|
|
|
|
|
|||||||||||||||
|
0 |
2 |
|
|
1 |
|
|
|
|
|
|
|
) |
5 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.10 |
Назад Вперёд |
Решение задачи 309.10
Воспользуемся формулой интегрирования по частям для определенного интеграла. Получим
∫ |
|
= , |
|
|
|
− |
0 |
− |
∫ |
− |
|
|
|
|
||
= , |
|
|
|
|
|
|||||||||||
|
|
= sin , |
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
= |
cos |
|
|
0 |
|
cos ) = |
||||
sin = |
|
|
− |
|
|
|
|
|
( |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −( · (−1) − |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
0) + sin 0 |
= |
+ 0 = . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться |
к условию] |
|||

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.11 |
Назад Вперёд |
Решение задачи 309.11
Воспользуемся методом интегрирования по частям. Получим
|
0 |
|
|
|
|
|
= − 2, |
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
||
∫ |
− |
|
|
|
= , |
|
|
|
− − |
|
|
|
3 |
∫ |
|
|
||||||||
|
3 |
|
|
3 |
|
|
= − |
|
|
|
|
|
|
|
|
3 |
− |
|
|
3 |
3 |
|
||
|
|
|
|
|
|
3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
( |
|
2) − |
|
= |
|
|
|
|
= 3( |
|
2) − |
|
|
|
+ 3 |
|
− |
|
= |
||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
= 3 − 3 |
|
|
|
|
|
|
|
|
− |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
= 6 − 15 − 9 − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
− 15 − 9 + 9 |
= −6 − 3. |
||||||||||||||
|
|
|
|
|
|
0 |
= 6 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию] |
||||||||
Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.12 |
Назад Вперёд |
Решение задачи 309.12
Разделим числитель и знаменатель подынтегральной дроби на √3 + 2. Получим
|
2 |
|
|
|
|
4√ |
|
|
− √ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4√ |
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32−+2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
2 − |
3 + 2 |
|
|
|
|
|
= |
|
|
|
|
|
. |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
∫ |
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
( |
|
|
|
|
|
|
|
|
− |
|
) |
|
|
|
|
|
|
|
|
|
|
|
∫ |
1 + 4 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 |
|
|
√3 + 2 + 4√2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
√ |
3 +2 |
|
(3 |
+ 2) |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(3 + 2) |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Выполним замену: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32−+2 |
|
|
= ,2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− |
2 |
|
2 2 |
|
|
|
+ 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −2 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
√ |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
+1 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∫ |
|
|
|
|
− |
|
(3 + 2) |
|
|
|
|
|
|
|
|
3 + 2 = |
|
3 2 |
+1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 + 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
4 |
|
3 −+2 |
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= (3−2+1)2 |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
3 +2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫1 |
|
1 + 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3 2 |
+ 1)2 |
|
|
|
|
|
|
|
4 ∫0 |
|
4 + 1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
4 |
|
|
|
(3 |
2 |
+ 1) |
2 |
|
|
|
16 |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
|
|
|
− |
|
|
|
|
|
|
|
|
1 4 |
|
− |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 309.12 |
Назад Вперёд |
Разделив числитель на знаменатель, получим |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
4 ∫0 |
4 + 1 |
|
4 |
∫0 |
( |
− 2 4 + 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
|
2 |
− |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 4 |
|
= |
1 |
|
|
|
1 |
+ |
2 |
|
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − 2 + 8 ln 5) = 32 . |
|||||||||||||||||||||
|
|
|
|
|
= 4 |
( |
2 |
|
− 2 + 8 ln |4 + 1|)0 |
= 4 |
( |
||||||||||||||||||||||||
|
|
|
|
|
|
|
1 2 |
|
|
1 |
|
|
1 |
1 1 1 1 |
ln 5 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию] |
|||||||
Часть II. Задачи Решения и указания
Глава 4. Теория интегрирования
Меню Решение задачи 310.1 |
Назад Вперёд |
Решение задачи 310.1
Сделаем рисунок.
y |
|
|
1 |
y = sin x |
|
|
|
|
O |
π |
x |
|
Рисунок Р.16 |
|
Воспользуемся формулой для вычисления площади криволинейной
трапеции |
∫ |
sin = − cos 0 |
= −(cos − cos 0) = −(−1 − 1) = 2. |
|
= |
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]
Часть II. Задачи Решения и указания
Глава 4. Теория интегрирования
Меню Решение задачи 311.1 |
Назад Вперёд |
Решение задачи 311.1
Сделаем рисунок.
y |
A |
y = √x3 |
b |
|
|
1 |
x |
|
|
O |
|
Рисунок Р.17 |
|
Для нахождения длины дуги кривой воспользуемся формулой (??). |
||||||||||||||||||||||||||||||||||
При этом ′ = ( 3/2)′ |
= 23 1/2. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 + 9 |
= , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
49 = , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫ √ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
= |
|
, |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||
= |
1 + |
|
|
|
= |
|
|
|
|
|
|
9 |
|
|
|
= |
|
|
|
√ |
|
|
|
|
= |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
4 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
4 |
|
∫ |
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
1 |
|
8 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(10√10 |
|
||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
1/2 = |
|
|
· |
|
|
· 3/2 |
= |
|
− 1). |
||||||||||||||
|
|
|
|
|
|
|
|
9 |
|
9 |
3 |
27 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]
Часть II. Задачи Решения и указания
Глава 4. Теория интегрирования
Меню Решение задачи 312.1 |
Назад Вперёд |
Решение задачи 312.1
Сделаем рисунок.
|
y |
|
|
|
y = 1 |
|
|
x |
|
|
x |
O |
1 |
4 |
|
|
Рисунок Р.18 |
Для вычисления объема тела, полученного вращением этой криволинейной трапеции вокруг оси , применим формулу (??):
= |
∫ |
( ) |
|
= − 1 = − (4 − 1) = 4 . |
||||||||||
|
4 |
1 |
|
2 |
1 |
|
4 |
1 |
3 |
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 313.1 |
Назад Вперёд |
Решение задачи 313.1
Среднее значение издержек можно вычислить по формуле
ср = 2 |
− 1 ∫1 |
( ) . |
||
|
|
1 |
2 |
|
Подставляя исходные значения в указанную формулу, получим
ср = 3 1 0 |
∫ |
(3 2 |
+ 4 + 2) = ( 3 + 2 2 |
+ 2 ) 0 = |
||
|
|
3 |
|
|
|
3 |
|
− |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 = 3(27 + 12 + 6 − 0) = 15.
Для того, чтобы найти объем продукции, при котором издержки принимают значение, равное 15, следует решить уравнение:
( ) = 15 |
|
3 2 + 4 + 2 = 15. |
||
Корнями этого уравнения являются числа 1 = |
5 |
и 2 = −3. По смыслу |
||
|
||||
3 |
||||
задачи искомый объем равен |
5 |
. |
|
[Вернуться к условию] |
3 |
|
|||
|
|
|
|
|

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 314.1 |
Назад Вперёд |
Решение задачи 314.1
Объем продукции , произведенной рабочим за промежуток времени от 1 до 2 выражается формулой
|
|
|
|
|
= ∫1 |
( ) . |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
В данном случае |
= ( |
3 ln |3 + 3| + 3 )1 |
|
|
|
|
|
|||||||||||
= |
∫ |
( |
3 + 4 + 3) |
= |
|
|
|
|
||||||||||
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
2 |
10 |
|
||
|
|
|
|
|
|
= |
|
ln 10 − |
|
ln 7 + 6 − 3 = |
|
ln |
|
+ 3. |
||||
|
|
|
|
|
|
3 |
3 |
3 |
7 |
|||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 315.1 |
Назад Вперёд |
Решение задачи 315.1
Несложно вычислить, |
|
что |
капиталовложения |
задаются |
функцией |
|||||||||||||||||||
( ) = + = |
10 + . В силу того, что |
дисконтированный доход |
||||||||||||||||||||||
за время вычисляется по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
= ∫0 |
|
( ) − 100 , |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в данном случае получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
∫ |
|
|
|
|
|
= 10 + , |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
= , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 |
0,08 |
|
|
|
= −0,08 , |
|
|
|
|
|
|
|
|||||||||||
= |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(10 + ) − |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
− |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
= |
|
12, 5 − |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0,08 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= −12, 5(10 + ) −0,08 0 |
+ 12, 5 |
∫ |
−0,08 = |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −162, 5 −0,24 + 125 − 156, 25 −0,08 0 |
= |
≈ |
|
||||||||||||||||||||
|
= |
− |
162, 5 − |
|
+ 125 |
− |
156, 25 − |
|
+ 156, 25 |
30, 5. |
||||||||||||||
|
|
0,24 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,24 |
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 316.1 |
Назад Вперёд |
Решение задачи 316.1
Pапас товаров на складе, образуемый за дней, можно вычислить с помощью формулы
∫
= ( ) .
0
В данном случае |
∫ |
|
+ 3 + 4) = ( 3 |
|
2 2 + 4 )0 |
|
|||
= |
(3 2 |
+ |
= 22. |
||||||
|
2 |
|
|
|
3 |
|
2 |
|
|
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 317.1 |
Назад Вперёд |
Решение задачи 317.1
По определению несобственного интеграла с бесконечным пределом интегрирования имеем:
∫ |
3 = |
→+∞ |
∫ |
− |
|
= |
→+∞ ( |
|
2 |
1 ) |
= →+∞ ( |
|
2 2 |
+ 2) |
= |
2. |
|||||
+∞ |
|
|
|
3 |
|
|
−2 |
|
|
|
− |
1 |
1 |
|
1 |
||||||
1 |
|
|
|
1 |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
lim |
|
|
|
|
lim |
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 317.3 |
Назад Вперёд |
Решение задачи 317.3
По определению несобственного интеграла с бесконечным пределом интегрирования имеем:
∫0 cos 3 = →+∞ |
∫0 |
cos 3 = |
|
|
|
|
|
|
|
|||
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
→+∞ ( 3 |
1 ) = 3 →+∞ |
|
|
||||||
|
|
|
− |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
1 |
sin 3 |
|
|
|
1 |
lim (sin 3 |
|
sin 3). |
|
|
|
|
|
|
|
|
|
|||||
Так как lim |
sin 3 не существует, то данный |
несобственный интеграл рас- |
||||||||||
→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
ходится. |
|
|
|
|
|
|
|
|
|
[Вернуться к условию] |
||

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 317.4 |
Назад Вперёд |
Решение задачи 317.4
По определению несобственного интеграла с бесконечным пределом интегрирования имеем:
|
|
∫1 |
(1 + 9 2) arctg2 3 |
= →+∞ |
∫1 |
|
(1 + 9 2) arctg2 3 . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Выполним замену arctg 3 = . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
arctg 3 = , |
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
= , |
|
|
|
|
|
|
|
|
arctg 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
∫1 |
(1 + 9 |
|
) arctg |
|
3 |
|
|
|
1+9 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||
|
|
|
|
|
|
|
|
|
− 3 |
· |
|
|
|
− 3 |
(arctg 3 − |
) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значит, исходный интеграл равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 3 |
( − ) |
|
|
||||||||||||||||||||||||||
∫1 |
(1 + 9 2) arctg2 |
3 = − |
3 →+∞ (arctg 3 − ) |
3 |
|||||||||||||||||||||||||||||||||||||||||
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
4 |
|
|
|
|
|
|
2 4 |
|
|
|
|
2 |
|
||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 318.1 |
Назад Вперёд |
Решение задачи 318.1
Подынтегральная функция ( ) = |
1 |
является неограниченной в любой |
||||||||||||||||
√ |
|
|||||||||||||||||
|
||||||||||||||||||
окрестности точки |
= 0. По определению несобственного интеграла от |
|||||||||||||||||
неограниченной функции имеем: |
(2 |
) |
→+0 2 − 2 |
|
|
|
||||||||||||
∫ √ |
→+0 |
∫ √ |
= →+0 |
|
= 2. |
|||||||||||||
1 |
|
|
|
1 |
|
|
|
√ |
|
|
1 |
|
√ |
|
|
|||
|
|
|
= |
lim |
|
|
|
lim |
|
|
|
= lim |
) |
|||||
0 |
|
|
|
|
|
|
|
|
|
|
( |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 318.2 |
Назад Вперёд |
Решение задачи 318.2
Найдим область определения подынтегральной функции. Для этого приравняем знаменатель к нулю:
9 2 |
− |
9 + 2, |
= 81 |
− |
72 |
− |
9, = |
9 − 3 |
= |
1 |
, |
|
= |
9 + 3 |
= |
2 |
. |
18 |
3 |
|
18 |
|
|||||||||||||
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|||||||
Таким образом заключаем, что подынтегральная функция является неограниченной в любой окрестности точки = 13 . Тогда, по определению несобственного интеграла от неограниченной функции имеем:
|
∫ |
1 |
9 |
|
|
|
9 + 2 |
|
9 → 31 − ∫ |
|
3 |
|
|
3 |
|
|
|
|
|
|||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
− |
|
|
|
|
|
1 |
|
|
|
|
|
− |
|
)( |
− |
|
) |
|
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
( |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
lim |
|
|
|
|
|
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|||||
Разложим подынтегральную дробь на простейшие: |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
= |
|
|
+ |
|
|
|
= |
− 32 + − 31 |
. |
|||||||||||||
( |
|
)( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
− 31 |
− 32 |
|
− 31 |
|
|
|
− 32 |
|
( |
− 31 |
)( |
− 32 |
) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Сравнивая коэффициенты в последнем и исходном числителе, составим и решим систему:
|
|
|
|
|
+ = 0, |
|
|
|
|
|
|
2= − 1, |
|
|
|
|
|
|
|
= −3, |
|
|
|
|
|
|
|||||||||||||
Тогда, |
|
|
2 |
|
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
− |
3 |
|
3 |
= 1; |
|
|
− |
3 |
|
+ 3 = 1; |
|
|
|
|
= 3; |
|
|
|
|
|
|
||||||||||||||||
∫ |
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
∫ |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
= 3 |
− |
|
|
|
|
|
|
+ |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
− |
)( |
|
− |
) |
|
|
|
|
0 |
|
− |
|
|
0 |
|
|
− |
|
|
|
|
1 |
|
|
2 |
|
|
2 |
||||||||
( |
|
|
|
1 |
0 |
|
− |
2 |
0) = 3 |
(− ln |
− |
1 |
|
+ ln |
|
− |
|
− ln |
|||||||||||||||||||||
= 3 (− ln |
− |
|
3 |
+ ln |
3 |
3 |
3 + ln |
3 |
3). |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 318.2 |
Назад Вперёд |
Окончательно, для исходного интеграла будем иметь
∫ |
1 |
9 2 |
|
9 + 2 |
|
3 → 31 − (− |
|
|
|
− |
3 |
3 |
|
|
|
− 3 − 3) |
|
∞ |
||||||||||
3 |
|
|
|
|
|
|
|
|||||||||||||||||||||
0 |
|
− |
|
= 1 lim |
|
|
|
|
1 |
|
+ ln 1 |
|
|
|
2 |
|
|
2 |
|
|
|
|||||||
|
|
|
|
ln |
|
|
|
|
+ ln |
|
|
|
ln |
|
= |
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. исходный интеграл расходится. |
|
|
|
|
|
|
|
|
[Вернуться к условию] |
|||||||||||||||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 4. Теория интегрирования |
|
Меню Решение задачи 318.5 |
Назад Вперёд |
Решение задачи 318.5
Подынтегральная функция ( ) = |
1 |
является неограниченной в любой |
( −3)2 |
окрестности точки = 3. По определению несобственного интеграла от неограниченной функции имеем:
∫0 |
( − 3)2 |
= →3−0 |
∫0 |
( − 3)2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
= →3−0 (− |
|
3 |
0) |
→3−0 (− |
|
3 − 3) = ∞. |
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
− |
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
lim |
|
1 |
|
|
|
= lim |
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Значит, данный интеграл расходится. |
|
|
|
[Вернуться к условию] |
|||||||||||||

Часть II. Задачи Решения и указания
Глава 5. Дифференцирование функций двух переменных
Меню |
Назад Вперёд |
Глава 5. Дифференцирование функций двух переменных

Часть II. Задачи Решения и указания
Глава 5. Дифференцирование функций двух переменных Меню Решение задачи 319.1 Назад Вперёд
Решение задачи 319.1
Подставляем в функцию абсциссу точки вместо , и ординату — вместо
: |
(2, 3 ) |
= 22 cos |
3 |
= 4 · 2 |
= 2. |
||||
|
|||||||||
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 320.1 |
Назад Вперёд |
Решение задачи 320.1
Область определения функции состоит из всех точек плоскости, для которых
1 − 2 − 2 > 0, |
2 + 2 6 1, |
и потому представляет собой круг с центром в начале координат и единичным радиусом, включающий свою границу — окружность.
[Вернуться к условию]

Часть II. Задачи Решения и указания
Глава 5. Дифференцирование функций двух переменных Меню Решение задачи 320.2 Назад Вперёд
Решение задачи 320.2
Координаты точек области определения удовлетворяют условию
− |
1 6 + 6 1, |
+ > 1, |
|
+ 6 1. |
|
Эта область представляет собой полосу, ограниченную параллельными пря- |
||
мыми + + 1 = 0 и + − 1 = 0. |
[Вернуться к условию] |
|

Часть II. Задачи Решения и указания
Глава 5. Дифференцирование функций двух переменных Меню Решение задачи 321.1 Назад Вперёд
Решение задачи 321.1
Являясь элементарной, данная функция непрерывна на всей своей области определения. Единственная точка разрыва — это нуль знаменателя, расположенный в начале координат (0; 0). [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 322.1 |
Назад Вперёд |
Решение задачи 322.1
Дифференцируем функцию по каждой из её переменных, считая другую переменную постоянной:
∂ |
= 4 3 cos2 , |
∂ |
= 4 · 2 cos (− sin ) = − 4 sin 2 . |
|
|
||
∂ |
∂ |
||
|
|
|
[Вернуться к условию] |

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 322.2 |
Назад Вперёд |
Решение задачи 322.2
Дифференцируем функцию по переменной , считая постоянной, а затем по переменной , считая постоянной:
∂ |
= 6 2 − 12 , |
∂ |
= −6 2 + 3 2. |
|
|
||
∂ |
∂ |
||
|
|
|
[Вернуться к условию] |

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 322.19 |
Назад Вперёд |
Решение задачи 322.19
При нахождении частных производных по каждой из трех переменных считаем остальные две переменные постоянными:
∂ |
= 2 2 ln , |
∂ |
= 2 2 ln , |
∂ |
= 2 2−1. |
|
∂ |
∂ |
∂ |
||||
|
|
|
||||
|
|
|
|
|
[Вернуться к условию] |

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 327.1 |
Назад Вперёд |
Решение задачи 327.1
Сначала находим частные производные первого порядка:
∂ |
= 4 3 + 8 3 + 7 , |
∂ |
= 12 2 2 + 7 . |
|
∂ |
∂ |
|||
|
|
Затем находим частные производные второго порядка:
∂2 |
= 12 2 |
+ 8 3, |
∂2 |
= |
∂2 |
= 24 2 |
+ 7, |
∂2 |
= 24 2 |
. |
|
∂ 2 |
∂ ∂ |
∂ ∂ |
∂ 2 |
||||||||
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 328.1 |
Назад Вперёд |
Решение задачи 328.1
Находим частные производные функции :
∂ |
= |
2 |
|
|
∂ |
= ln( 2 − 2) − |
2 2 |
|
|
|
, |
|
|
|
. |
||
∂ |
2 − 2 |
∂ |
2 − 2 |
|||||
Подставляем найденные выражения в левую часть уравнения:
2 − 2 |
+ |
(ln( 2 − 2) − 2 − 2 ) |
= |
|
|
|
|
|
|
|
||||||
1 2 |
1 |
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
||
|
|
= |
|
2 |
+ ln( 2 − 2) |
− |
2 |
= |
ln( 2 − 2) |
= |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − 2 |
|
|
|
2 − 2 |
|
|
2 |
|
2 |
||||
Получили, что левая часть уравнения тождественно равна правой. А это и значит, что функция удовлетворяет данному уравнению.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 331.1 |
Назад Вперёд |
Решение задачи 331.1
Находим частные производные:
∂ |
= |
|
|
|
|
, |
|
∂ |
= |
|
|
− |
. |
|
|
|
|
|
|
|
|
||||||
∂ |
|
√ 2 − 2 |
|
|
∂ |
|
√ 2 − 2 |
||||||
Выписываем полный дифференциал в виде (5.4):
= |
− |
. |
||
|
|
|
||
|
√ 2 − 2 |
|||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 331.18 |
Назад Вперёд |
Решение задачи 331.18
Находим частные производные:
′ |
= |
1 |
, ′ |
= |
|
|
− |
, ′ |
= |
|
|
− |
. |
||
|
|
|
|
|
|
|
|||||||||
|
|
√ 2 + 2 |
|
|
√( 2 + 2)3 |
|
|
√( 2 + 2)3 |
|||||||
Выписываем полный дифференциал (5.4):
= |
|
|
− |
+ |
|||
|
|
|
|
|
. |
||
√ |
|
√ |
|
|
|||
2 + 2 |
( 2 + 2)3 |
||||||
|
|
|
|
|
|
[Вернуться к условию] |
|

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 333.1 |
Назад Вперёд |
Решение задачи 333.1
Число 1,073,97 представляет собой |
значение |
функции |
( , ) |
= при |
|||||
= 1,07 и = 3,97. Легко вычислить, что при 0 = 1 и 0 = 4 |
|
||||||||
( 0; 0) = 14 = 1. |
|
|
|
|
|||||
Находим приращения переменных: |
|
|
|
|
|
|
|
|
|
= − 0 = 1,07 − 1 = 0,07, |
= − 0 = 3,97 − 4 = −0,03. |
||||||||
Вычисляем частные производные в точке ( 0; 0): |
|
|
|
|
|||||
′ = −1, |
′( |
0 |
, |
0 |
) = 4 |
· |
14−1 |
= 4, |
|
|
|
|
|
|
|
|
|||
′ = ln , |
′( |
0 |
, |
0 |
) = 14 ln 1 = 0. |
|
|||
|
|
|
|
|
|
|
|
||
Находим приближённое значение ( , ), заменяя приращение функции полным дифференциалом:
( , ) = ( 0, 0) + ≈ ( 0, 0) + =
=( 0, 0) + ′( 0, 0)Δ + ′( 0, 0)Δ =
=1 + 4 · 0,07 + 0 · (−0,03) = 1 + 0,28 = 1,28.
[Вернуться к условию]

Часть II. Задачи Решения и указания
Глава 5. Дифференцирование функций двух переменных Меню Указание к задаче 333.6 Назад Вперёд
Указание к задаче 333.6
Принять = 3,14. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Указание к задаче 333.9 |
Назад Вперёд |
Указание к задаче 333.9
Выразить приращения аргументов в радианах, считая, что = 3,14. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 334.1 |
Назад Вперёд |
Решение задачи 334.1
Не прибегая к формуле (5.5) производной сложной функции, просто подставим и в :
( ) = 2 cos2 + 2 sin2 = 2(cos2 +sin2 ) = 2 .
Так как производная постоянной равна нулю, то окончательно получаем:
|
|
= 0. |
[Вернуться к условию] |
|
|
||
|
|
|

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 334.4 |
Назад Вперёд |
Решение задачи 334.4
Здесь непосредственная подстановка приводит к усложнению выкладок и результата. Применяем формулу (5.5) для производной сложной функции:
|
= |
∂ |
+ |
∂ |
= (5 4 |
+ 2 )(−2 sin 2 ) + (2 − 3 2) |
1 |
= |
||||
|
|
|
|
|
|
|
|
|||||
|
∂ |
∂ |
1 + 2 |
|||||||||
=−2(5 4 + 2 ) sin 2 + 2 − 3 2 . 1 + 2
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 334.8 |
Назад Вперёд |
Решение задачи 334.8
По формуле (5.5) производной сложной функции
|
= |
|
∂ |
+ |
∂ |
+ |
∂ |
= ( + ) cos + ( + ) |
1 |
+ ( ) = |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∂ |
∂ |
∂ |
|
|||||||||||||||||
|
|
|
= (1 + ) |
( cos + ) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 335.1 |
Назад Вперёд |
Решение задачи 335.1
Выписываем направляющие косинусы заданного направления: |
|
|
|||||||||||||
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
||||
cos = cos |
|
= |
|
|
|
, |
cos = cos ( |
|
− |
|
) = cos |
|
= |
|
. |
3 |
2 |
2 |
3 |
6 |
2 |
||||||||||
Находим частные производные функции в точке :
∂ |
= 2 , |
∂ |
(1; 1) = 2, |
∂ |
= 2 , |
∂ |
(1; 1) = 2. |
|
|
|
|
||||
∂ |
∂ |
∂ |
∂ |
√
Тогда по формуле (5.7) ∂∂ = 2· 23 +2· 12 = √3+1. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 340.1 |
Назад Вперёд |
Решение задачи 340.1
Находим частные производные функции и их значения в точке :
′ |
= 2 , |
′ |
(2; |
− |
1) = 4, |
|
′ |
= 4 , |
′ |
(2; |
− |
1) = |
− |
4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда grad = ( ′ |
( ); ′ ( )) |
= (4; −4). |
|
|
|
[Вернуться к условию] |
|||||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 341.1 |
Назад Вперёд |
Решение задачи 341.1
По определению
grad = ( ′ , ′ , ′ ) = (2 , 2 3, 3 2 2).
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 342.1 |
Назад Вперёд |
Решение задачи 342.1
По определению градиента
grad = ( ′ , ′ , ′ ) = (2 − 1, −2 + , ) .
Подставим координаты точки :
grad ( ) = (2 · 1 − 1, −2 · 0 + (−1), 0) = (1, −1, 0) .
Находим модуль градиента, определяющий значение максимального роста
функции : √ √
| grad | = 12 + (−1)2 + 02 = 2.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 344 |
Назад Вперёд |
Решение задачи 344
Производная
′ = 2
показывает, что при одном и том же расстоянии между городами увеличение потока пассажиров пропорционально удвоенному числу жителей. Производ-
ная
′ = − 22
показывает, что при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 345.2 |
Назад Вперёд |
Решение задачи 345.2
Выполняем дифференцирование:
′ |
= |
1 |
(1 |
− |
|
)( |
− |
|
)− 1 |
= |
− 1 , |
|
1 − 1 |
||||||||||||
|
|
|
1 |
|
1 |
|
1 |
|
||||
′ |
= |
2 |
(1 |
− |
|
)( |
− |
|
)− 2 |
= |
− 2 . |
|
1 − 2 |
||||||||||||
|
|
|
2 |
|
2 |
|
2 |
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 348.1 |
Назад Вперёд |
Решение задачи 348.1
В данном случае
|
|
ln |
|
|
|
ln |
|
|
|
ln |
|
|
|
ln |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ln |
−1 |
= − |
ln |
= − |
|
(ln − ln |
) |
= |
ln |
= 1. |
||||||||||
= − |
−1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 349.1 |
Назад Вперёд |
Решение задачи 349.1
Находим частные производные:
′ |
= 2 + |
− |
2, |
′ |
= + 2 |
− |
3. |
|
|
|
|
|
|
Находим подозрительные на экстремум, то есть стационарные, точки:
Отсюда |
′ = 0, |
2 + − 2 = 0, |
2 + − 2 = 0, |
||||||||||
|
|
|
− |
|
− |
|
|
|
|||||
|
′ = 0, |
|
+ 2 |
|
3 = 0, |
|
3 + 1 = 0. |
||||||
|
|
1 |
|
|
|
|
2 |
4 |
|
||||
|
|
= |
|
, |
|
= 2 − 2 |
= 2 − |
|
|
= |
|
. |
|
|
|
3 |
3 |
3 |
|||||||||
Таким образом, единственной стационарной точкой функции является
точка 0(13 , 43 ).
Находим частные производные второго порядка:
′′ |
= 2, ′′ = 1, |
′′ |
= 2. |
|
|
|
|
Отсюда имеем, что в точке 0 |
|
|
|
= ′′ ( 0) = 2, |
= ′′ ( 0) = 1, |
= ′′ ( 0) = 2, |
|
|
= − 2 = 3. |
|
|
Так как > 0 и > 0, то согласно теореме 5.8 в точке 0 данная функция имеет минимум, причём
min = |
( |
3 |
, |
3) |
= |
9 |
+ 9 |
+ |
9 |
− 3 |
− 4 = |
3 |
− 4 = −3. |
|
|
|
1 |
|
4 |
|
1 |
4 |
|
16 |
2 |
|
5 |
7 |
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 350.1 |
Назад Вперёд |
Решение задачи 350.1
Находим частные производные функции :
= 2 2 |
− |
3 |
− |
2 2, |
′ |
= 4 |
− |
3 2 |
|
− |
2 2, |
′ |
= 2 2 |
− |
3 |
− |
2 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ищем стационарные точки внутри треугольника :
′ |
|
|
|
2 |
− 33 |
−2 |
2 |
|
− |
|
− |
|
|
= 0, |
|
4 |
2 |
2 2 = 0, |
(4 |
|
3 |
|
2 ) = 0, |
||
|
|
|
− − 2 = 0, |
|
(2 |
− − 2 ) = 0. |
||||||
′ = 0, |
2 |
|
|
|||||||||
Внутри треугольника , где > 0 и > 0, полученная система равносильна следующей:
4 − 3 − 2 = 0, |
= 2 − 2 , |
= 2 − 2 , |
||||
|
− |
− 2 |
= 0, |
|
0 |
|
2 |
4 |
− 3(2 − 2 ) − 2 = 0, |
4 = 2. |
|||
Отсюда имеем стационарную точку (1; 1/2), очевидно, лежащую внутри
треугольника (рисунок Р.19). Для этой точки |
|
4. |
||
( 0) = 12 · 2 · (2 − 1 − 2) |
= |
|||
1 |
|
1 |
|
1 |
Исследуем функцию на границе |
области. |
На сторонах = 0 и |
||
= 0 треугольника функция принимает нулевые значения. На стороне+ = 6, воспользовавшись тем, что = 6 − , представим функцию как функцию 1( ) одной переменной , заданную на отрезке [0; 6]:
1( ) = 2(6 − )(2 − − (6 − )) |
= (6 2 − 3) · (−4) = 4 3 − 24 2. |
||||||
Ищем стационарные точки функции 1( ): |
|
|
|
||||
′ ( ) = 0, |
12 2 |
− |
48 = 0, |
( |
− |
4) = 0. |
|
1 |
|
|
|
|
|
||
Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 350.1 |
Назад Вперёд |
y 
6
O
x
+ y
= 6
M1
b
M0
b
6 x
Рисунок Р.19
Имеем два корня: = 0 и = 4. Из них только = 4 лежит внутри интервала (0; 6). Ему соответствуют точка 1(4; 2), в которой
( 1) = 1(4) = 4 · 43 − 24 · 42 = 16(16 − 24) = −128.
На концах отрезка [0; 6], соответствующих вершинам (6; 0) и (0; 6) треугольника , функция 1( ), очевидно, обращается в нуль.
Мы доказали, что наименьшее и наибольшее значения функции в треугольнике может достигаться либо на сторонах = 0 и = 0, где она обращается в нуль, либо в точках 0 и 1. Следовательно,
min = ( 1) = −128, |
max = ( 0) = |
1 |
. |
|
|||
4 |
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 351.1 |
Назад Вперёд |
Решение задачи 351.1
Найдем стационарные точки функции : |
= 2, |
|||
′ = 0, |
2 − 4 = 0, |
|||
|
|
|
− |
1. |
′ = 0, |
2 + 2 = 0, |
= |
|
|
Имеем единственную стационарную точку 0(2, −1), которая принадлежит области . Вычисляем значение функции в этой точке:
( 0) = 4 + 1 − 8 − 2 = −5.
Для поиска максимума и минимума на границе применим метод множителей Лагранжа. Строим функцию Лагранжа:
|
|
|
( , , ) = 2 |
|
+ 2 − 4 + 2 + ( 2 |
+ 2 − 45). |
|
|
||||||||||||||||||||
Находим стационарные точки функции Лагранжа: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
′ = 0, |
|
|
2 − 4 + 2 = 0, |
|
|
|
= 1+2 1, |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
||||
′ = 0, |
|
|
2 |
+ 2 + 2 |
= 0, |
|
|
|
= − |
|
, |
|
|
|
|
|||||||||||||
|
|
|
|
1+ |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
+ − 45 = 0, |
|
|
|
|
|
+ − 45 = 0, |
||||||||||||||||
′ = 0, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Подставляем значения и из двух первых уравнений в третье: |
|
|
||||||||||||||||||||||||||
|
4 |
|
+ |
|
1 |
|
|
= 45, |
|
5 |
|
|
|
= 45, (1 + )2 = |
1 |
. |
||||||||||||
(1 + |
)2 |
|
(1 + )2 |
(1 + |
)2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
||||||||||||
Отсюда имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 + |
1 = |
|
, |
1 + |
2 = − |
|
, |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
||||||||||||||
1 = |
2 |
= 6, |
1 = − |
1 |
= −3, |
2 = |
|
2 |
= −6, 1 |
= − |
1 |
= 3. |
||||||||||||||||
1 |
1 |
1 |
1 |
|||||||||||||||||||||||||
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
−3 |
|
|
||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 351.1 |
Назад Вперёд |
Итак, на границе обнаружены две стационарные точки функции Лагранжа:1(6, −3) и 2(−6, 3). В этих точках
( 1) = 36 + 9 − 24 − 6 = 15, |
( 2) = 36 + 9 + 24 + 6 = 75. |
Сравнивая значения функции в точках 0, 1 и 2, приходим к |
|
выводу, что |
|
min = (2, −1) = −5, |
max = (−6, 3) = 75. |
|
[Вернуться к условию] |

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 353.1 |
Назад Вперёд |
Решение задачи 353.1
Приравнивая ординаты данных двух линий, приходим квадратному уравнению
2 = − 5, 2 − + 5 = 0,
не имеющему решений. Это значит, что данные парабола и прямая не имеют общих точек, что также видно из рисунка Р.20.
Возьмем произвольную точку ( ; 2) параболы и ( ; − 5) прямой. Тогда квадрат расстояния между этими точками, который мы будем обозначать через ( , ), может быть вычислен по формуле
( , ) = ( − )2 + ( 2 − + 5)2.
Для решения поставленной задачи достаточно найти минимум функции
( , ).
Находим стационарные точки функции :
′ = 0, |
|
2( |
− |
) + 4 ( 2 |
− |
+ 5) = 0, |
|||
|
− |
|
|
|
|
|
|||
|
|
− |
) |
− |
2( 2 |
− |
+ 5) = 0. |
||
′ = 0, |
|
2( |
|
|
|
||||
Сложим оба уравнения:
(4 − 2)( 2 − + 5) = 0.
Если бы выполнялось равенство 2 − + 5 = 0, то из второго уравнения системы следовало бы, что и − = 0. А это бы значило, что парабола и прямая имеют общую точку, что, как мы уже знаем, неверно. Таким образом,
4 − 2 = 0, |
= |
1 |
. |
|
|||
2 |
Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 353.1 |
Назад Вперёд |
Подставим полученное значение во второе уравнение системы:
−2 |
(2 |
− ) − 2 |
(4 − + 5) |
= 0, |
4 = 2 , |
= 8 . |
|
|
1 |
|
1 |
|
23 |
|
23 |
Делаем вывод, что единственной стационарной точкой функции ( , ) является точка 0(1/2; 23/8).
y 
y = x2
|
|
x − y − 5 = 0 |
b12 ; 14
O |
|
|
|
x |
|
8 ; − |
8 |
|
|
b |
|
|
|
|
|
23 |
|
17 |
|
Рисунок Р.20
Из геометрических соображений (рисунок Р.20) ясно, минимум функции ( , ) достигается в некоторой точке, которая согласно необходимому условию локального экстремума является стационарной точкой функции( , ). Этой точкой будет 0, поскольку других стационарных точке функция ( , ) не имеет. Итак, расстояние между данными параболой и прямой

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 353.1 |
Назад Вперёд |
совпадает с расстоянием между их точками (1/2; 1/4) и (23/8; −17/8) и равно
√ ( 0) = |
√(2 − |
8 ) |
|
+ (4 − |
|
8 + 5) |
= |
||||||||||||
|
|
|
|
1 |
|
23 |
2 |
|
|
1 |
23 |
|
|
2 |
|||||
|
√( |
|
|
|
|
|
8 ) |
|
|
|
|
|
|
|
|
||||
= |
8 ) |
+ ( |
= |
8 . |
|
||||||||||||||
|
|
|
|
19 |
|
2 |
|
|
19 |
|
2 |
|
19√ |
2 |
|
|
|||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 355 |
Назад Вперёд |
Решение задачи 355
Прибыль равна разности выручки и издержек:
( , ) = 8 + 10 − 2 − − 2.
Ищем стационарные точки функции прибыли: |
= 2, |
|
|
|
|||||||
8 − 2 − = 0, |
8 − 2 − = 0, |
|
· |
|
|||||||
|
− |
|
− |
2 = 0, |
− |
6 + 3 = 0, |
|
− |
2 |
2 = 4. |
|
10 |
|
|
|
= 8 |
|
|
|||||
Имеем стационарную точку 0(2, 4). Вычисляем вторые производные функции ( , ):
= ′′ |
= |
− |
2, |
= ′′ |
= |
− |
1, |
= ′′ |
= |
− |
2. |
|
|
|
|
|
|
|
|
|
Так как = − 2 = 3 > 0 и < 0, то по теореме 5.8 точка 0 является точкой локального максимума прибыли, причем
max = ( 0) = 8 · 2 + 10 · 4 − 22 − 2 · 4 − 42 = 28.
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 357 |
Назад Вперёд |
Решение задачи 357
Обозначим через м, м и м длину, ширину и глубину бассейна. По условию
32
= = м.
Определим, при каких значениях и площадь бассейна
= + 2 + 2 = + |
64 |
+ |
64 |
||
|
|
|
|
||
|
|
|
|
||
будет минимальной. Находим частные производные площади = ( , ):
′ |
= |
− |
64 |
, |
′ |
= |
− |
64 |
. |
2 |
|
||||||||
|
|
|
|
|
2 |
||||
Находим стационарные точки функции ( , ) при > 0 и > 0:
′ |
|
|
|
|
− |
|
|
|
2 |
|
||
|
|
|
= 0, |
|
− |
642 |
= 0, |
|
2 |
= 64, |
||
( |
|
) = 0, |
|
|
|
|
|
|||||
′ |
|
= 0, |
|
|
642 |
= 0, |
|
|
= 64, |
|||
|
2 |
|
− |
|
|
|
|
3= , |
|
|
= 4, |
|
|
|
= 64, |
|
|
|
= 64, |
|
|
|
|||
|
|
|
|
|
|
|
= 4. |
|||||
Имеем единственную стационарную точку 0(4, 4). Из практических соображений ясно, что функция ( , ) достигает своего минимума в некоторой конечной точке, лежащей внутри первой координатной четверти (попытайтесь доказать это строго математически). Эта точка является стационарной и, следовательно, совпадает с 0.
Таким образом бассейн должен иметь длину и ширину, равные 4 метра. Его глубина
3232
= = 4 · 4 = 2 м.

Часть II. Задачи |
|
Решения и указания |
|
Глава 5. Дифференцирование функций двух переменных |
|
Меню Решение задачи 357 |
Назад Вперёд |
[Вернуться к условию]

Часть II. Задачи Решения и указания
Глава 5. Дифференцирование функций двух переменных Меню Указание к задаче 365 Назад Вперёд
Указание к задаче 365
Смотри задачу 353.1. [Вернуться к условию]

Часть II. Задачи Решения и указания
Глава 6. Дифференциальные уравнения
Меню |
Назад Вперёд |
Глава 6. Дифференциальные уравнения

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 366.1 |
Назад Вперёд |
Решение задачи 366.1
Продифференцируем по данное равенство:
′ = .
Подставим вместо в исходное равенство:
= ′ |
или ′ − = 0. |
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 366.5 |
Назад Вперёд |
Решение задачи 366.5
Продифференцируем по данное равенство:
2 ′ = 2 |
или |
= ′. |
Подставим вместо в исходное равенство: |
||
2 = 2 ′ |
или |
= 2 ′ . |
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 367.1 |
Назад Вперёд |
Решение задачи 367.1
Это уравнение вида ′′′ = ( ). Интегрируя, получим |
|
|||||||
|
|
′′ = ∫ |
6 |
= −3 −2 + 1, |
|
|||
|
3 |
|
||||||
|
′ = ∫ |
(−3 −2 + 1) = + 1 + 2, |
||||||
|
|
|
|
|
3 |
|
|
|
= ∫ |
( + 1 |
+ 2) = 3 ln | | + 2 1 2 |
+ 2 + 3. |
|||||
|
3 |
|
|
1 |
|
|||
или
= 3 ln | | + 1 2 + 2 + 3.
[Вернуться к условию]

Часть II. Задачи Решения и указания
Глава 6. Дифференциальные уравнения Меню Решение задачи 367.4 Назад Вперёд
Решение задачи 367.4
Это уравнение вида ′′ = ( ). Интегрируя, получим
|
′ = ∫ |
3 sin2 cos = 3 |
∫ |
sin2 (sin ) = sin3 + 1, |
|
|||
= ∫ |
(sin3 + 1) = 1 − ∫ |
(1 − cos2 ) (cos ) = |
|
|||||
|
|
|
|
|
1 |
cos3 + 1 |
|
|
|
|
|
|
|
= − cos + |
|
+ 2. |
|
|
|
|
|
|
3 |
|||
Для нахождения частного решения, воспользуемся начальными условиями
1 |
= −1 + |
1 |
+ 2 |
, |
|
|
|||
3 |
3 |
|||
|
0 = 0 + 1. |
|
||
Отсюда, 1 = 0, 2 = 1. Окончательно,
= − cos + 13 cos3 + 1.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 368.1 |
Назад Вперёд |
Решение задачи 368.1
Это уравнение с разделяющимися переменными. Поэтому,
|
+ ( + 1) = 0 |
( + 1) = − . |
||||||
Разделим переменные. Получим |
|
|
|
|||||
|
|
|
|
|
= − |
|
||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
+ 1 |
|||
Проинтегрируем обе части уравнения. Имеем |
||||||||
∫ = − ∫ |
+ 1 |
ln | | = − + ln | + 1| + ln | |. |
||||||
|
|
|
|
|
|
|
||
Преобразуем полученное равенство, воспользовавшись свойствами логарифмов:
= ( + 1) − .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 368.6 |
Назад Вперёд |
Решение задачи 368.6
Это уравнение с разделяющимися переменными. Поэтому,
|
|
|
|
|
|
= (2 + 1). |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разделим переменные. Получим |
|
|
||||||
|
|
|
|
|
= (2 + 1) . |
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
Проинтегрируем обе части уравнения. Имеем |
||||||||
∫ |
|
= ∫ |
(2 + 1) |
ln | | = 2 + + ln | |. |
||||
|
||||||||
Преобразуем полученное равенство, воспользовавшись свойствами лога-
рифмов:
= 2+ .
Найтем частное решение, удовлетворяющее данному начальному условию:
1 = 0.
Откуда = 1. Осталось подставить найденное значение в общее решение:
= 2+ .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 369.1 |
Назад Вперёд |
Решение задачи 369.1
Это однородное уравнение. Сделаем замену: = , = + . Подставим в исходное уравнение:
( + ) − (1 + ) = 0,
+ − (1 + ) = 0.
Получили уравнение с разделяющимися переменными. Перенесем слагаемые, содержащие вправо:
= (1 + ) − ,
= .
Разделим переменные и проинтегрируем:
|
= |
|
, |
|
|
|
|
||
|
|
|||
∫ |
= |
∫ |
|
. |
|
Откуда = ln | | + . Учитывая замену, получим общее решение уравнения:
= (ln | | + ).
Для нахождения частного решения используем начальное условие:
2 = 1 · (ln 1 + ).
Значит, = 2. Тогда частное решение имеет вид:
= (ln | | + 2).
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 369.2 |
Назад Вперёд |
Решение задачи 369.2
Это однородное уравнение. Сделаем замену: = , ′ = ′ + . Подставим в исходное уравнение:
′ + = ln ,
′ + = ln .
Получили уравнение с разделяющимися переменными. Произведем необходимые преобразования:
|
|
|
|
= ln − , |
||||||||
|
|
|
|
|
||||||||
|
|
|||||||||||
|
|
|
= (ln − 1). |
|||||||||
|
|
|
||||||||||
|
|
|||||||||||
Разделим переменные и проинтегрируем: |
|
|
|
|
|
|||||||
|
|
|
|
|
|
= |
|
|
|
, |
|
|
|
|
|
|
|
|
|
||||||
∫ |
(ln − 1) |
|
|
|
||||||||
(ln − 1) |
= |
∫ |
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Откуда
ln | ln − 1| = ln | | + ln | |, ln = + 1, = +1.
Учитывая замену, получим общее решение уравнения:
= +1.

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 369.2 |
Назад Вперёд |
Для нахождения частного решения используем начальное условие:
1 = 1 · +1.
Значит, = −1. Тогда частное решение имеет вид:
= 1− .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 369.12 |
Назад Вперёд |
Решение задачи 369.12
Представим уравнение в виде:
′ = + 2 + 1. 2 − 3
Это уравнение можно привести к однородному. Для этого решим систему:
+ 2 + 1 = 0,
2 − 3 = 0.
3 |
= − |
5 |
. Сделаем замену |
|||||||||||
Решение этой системы 0 = 2 , 0 |
4 |
|||||||||||||
= + 0, |
|
= + 0, |
|
|||||||||||
т.е. |
3 |
|
|
|
|
|
|
|
5 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
= + |
|
|
, |
|
= |
− |
|
. |
|
|||||
2 |
|
4 |
|
|||||||||||
Получим |
|
|
|
|
|
|
23 |
|
|
3) |
|
|||
|
2 +( |
|
|
|
||||||||||
′ = |
+ |
23 + 2 |
|
− 45 + 1 |
, |
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
′ |
|
( + 2) |
− |
|
|
|
|
||||||
|
= |
|
|
2 |
|
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Получили однородное уравнение. Решим его стандартным образом. Пусть
= , ′ = ′ + . Тогда
′ + = |
+ 2 |
, |
||||||
|
|
2 |
|
|||||
|
|
|
|
|
|
|
||
′ + = |
1 + 2 |
, |
|
|||||
|
2 |
|
||||||
|
|
|
|
|
|
|
||
|
|
= |
1 |
|
|
|||
|
|
|
|
. |
|
|
||
|
2 |
|
|
|||||

Часть II. Задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решения и указания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Глава 6. Дифференциальные уравнения |
|
|
|
|
|
|
|
|
|||||||||||
Меню Решение задачи 369.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Назад Вперёд |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разделим переменные и проинтегрируем: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||||
|
|
∫ |
|
2 |
|
|
|
|
|
|
|||||||||
|
|
= |
∫ |
2 . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Откуда |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
| | + . |
|
|
|
|
|
|||||||||
|
|
= |
|
|
ln |
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
||||||||||||||
Произведем обратные замены: |
(2 ln | | + ), |
|
|
||||||||||||||||
|
|
= |
|
|
|||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
и окончательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ) |
|
||
+ 4 = ( − 2)(2 ln − 2 |
, |
||||||||||||||||||
|
5 |
3 |
|
|
|
1 |
|
|
3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 + 5 = (2 − 3) (ln |
|
3 |
|
|
|
||||||||||||||
− |
2 |
+ ). |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 370.1 |
Назад Вперёд |
Решение задачи 370.1
Это линейное уравнение. Решим его двумя способами.
1 способ (метод Лагранжа). Найдем сначала общее решение соответствующего однородного уравнения
|
′ − = 0, |
|
|
|
||||
|
|
|
|
= . |
||||
|
|
|||||||
Разделяя переменные и интегрируя, получим |
|
|||||||
|
|
= , |
∫ |
|
= ∫ |
. |
||
|
|
|
||||||
Откуда ln | | = + ln | | или = . Общее решение заданного уравнения ищем в виде
= ( ) ,
где ( ) — некоторая функция. Найдем
′ = ′( ) + ( ) .
Подставим в исходное уравнение
′( ) + ( ) − ( ) = .
Отсюда, ′( ) = 1 или ( ) = + . Следовательно, общее решение данного уравнения
= ( + ) .
2 способ (метод Бернулли). Полагаем = , где = ( ), = ( ) — некоторые функции от , тогда ′ = ′ + ′ . Подставим в данное уравнение
′ + ′ − = , ′ + ( ′ − ) = .

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 370.1 |
Назад Вперёд |
Подберем функцию = ( ) так, чтобы выражене в скобках равнялось нулю, т.е. решим уравнение с разделяющимися переменными
′ − = 0, |
|
= , |
|
= . |
|
|
|||
|
|
Откуда ln | | = + ln | | или = . Поскольку нам достаточно какогонибудь одного ненулевого решения уравнения, то возьмем = (положили= 1). Подставим найденное в последнее уравнение
′ = , |
′ = 1. |
Значит, = + . Производя обратную замену, получим общее решение исходного уравнения
= ( + ) .
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 370.5 |
Назад Вперёд |
Решение задачи 370.5
Запишем уравнение в виде
2 ′ − = 2.
Это уравнение Бернулли. С помощью замены = 1 его можно свести к линейному, однако удобнее сразу решать его методом Бернулли.
Полагаем = , где = ( ), = ( ) — некоторые функции от , тогда ′ = ′ + ′ . Подставим в данное уравнение
2( ′ + ′ ) − = 2 2, 2 ′ + ( ′ − ) = 2 2.
Подберем функцию = ( ) так, чтобы выражене в скобках равнялось нулю, т.е. решим уравнение с разделяющимися переменными
′ − = 0, |
|
|
= , |
|
= |
|
||
|
|
|
|
|
. |
|||
|
|
|
||||||
Откуда ln | | = ln | | + ln | | или = . Поскольку нам достаточно какогонибудь одного ненулевого решения уравнения, то возьмем = (положили= 1). Подставим найденное в последнее уравнение
|
|
3 ′ = 2 2, |
|
|
|
= |
|
. |
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
||||
Значит, |
1 |
|
|
|
|
|
|
1 |
|
|
− |
= ln | | − , |
= |
|
|
. |
|||||
|
|
|
||||||||
|
− ln | | |
|||||||||
Производя обратную замену, получим общее решение исходного уравнения
= − ln .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 370.13 |
Назад Вперёд |
Решение задачи 370.13
Данное уравнение не является линейным относительно и ′, но является таковым относительно и ′. Поэтому преобразуем его следующим образом
+ 2 + ′ = 0, ′ + = − 2.
Решим это уравнение методом Бернулли. Полагаем = , где = ( ),= ( ) — некоторые функции от , тогда ′ = ′ + ′ . Подставим в данное уравнение
′ + ′ + = − 2, ′ + ( ′ + ) = − 2.
Подберем функцию = ( ) так, чтобы выражене в скобках равнялось нулю, т.е. решим уравнение с разделяющимися переменными
′ + = 0, |
|
= − , |
|
= − . |
|
|
|||
|
|
Откуда ln | | = − + ln | | или = − . Поскольку нам достаточно какогонибудь одного ненулевого решения уравнения, то возьмем = − (положили = 1). Подставим найденное в последнее уравнение
′ − = − 2, |
= − 2 . |
Значит,
= − 2 + 2 − 2 + .
Производя обратную замену, получим общее решение исходного уравнения
= (− 2 + 2 − 2 + ) − = − − 2 + 2 − 2.
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 371 |
Назад Вперёд |
Решение задачи 371
Модель роста в условиях конкурентного рынка в данном случае задается уравнением
′ = (2 − ) .
Разделяя переменные и интегрируя, получим
( |
− |
2) |
|
|
|
|
|
− |
| | |
|
|
|
= , |
ln |
|
− 2 |
|
= 2 + ln . |
|||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Откуда
− 2 = −2
или
2
= 1 −
Принимая во внимание начальное условие, найдем константу :
1 |
= |
2 |
= −3. |
|
|
|
|
||
2 |
1 − 0 |
|||
Таким образом, объем реализованной продукции описывается равенством
2= 1 + 3 −2 .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 372 |
Назад Вперёд |
Решение задачи 372
В данном случае функция дохода удовлетворяет уравнению
( ) = 12 ′( ) + 2
или
′( ) − 2 ( ) = −4 .
Полученное уравнение является линейным неоднородным уравнением первого порядка. Положим = , ′ = ′ + ′. Тогда
′ + ′ − 2 = −4 , |
′ + ( ′ − 2 ) = −4 . |
||||||
Определим функцию : |
|
|
|
|
|
||
|
|
|
|
ln | | = 2 , |
|||
|
|
|
= 2 , |
|
= 2 , |
||
|
|
|
|||||
откуда = 2 . Осталось определить функцию : |
|||||||
|
|
|
′ 2 = −4 , |
′ = −4 −2 . |
|||
Интегрируя, получим
= 2 −2 + −2 + .
Значит,
= = (2 −2 + −2 + ) 2 = 2 + 1 + 2 .
Используя начальное условие (0) = 2, найдем постоянную :
2 = 1 + ,
откуда = 1. Окончательно, функция дохода имеет вид
= 2 + 1 + 2 .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 373 |
Назад Вперёд |
Решение задачи 373
Решим уравнение
′ = 101 .
Разделяя переменные и интегрируя, получим
|
= |
1 |
, |
ln | | = |
1 |
+ ln | |, |
|
|
|
|
|
||||
|
10 |
10 |
|||||
откуда = 10 . Так как первоначальная сумма равна , то
= 0, |
= , |
т.е. = 10 . Теперь найдем момент времени, когда сумма вклада удвоится, т.е. станет равной 2 :
2 = |
|
, |
|
|
= 2. |
10 |
10 |
Значит,
= 10 · ln 2 ≈ 6, 93.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 374.1 |
Назад Вперёд |
Решение задачи 374.1
Составим и решим характеристическое уравнение:
|
2 − 5 + 4 = 0, |
|
||
|
= 25 − 16 = 9, |
|
||
1 = |
5 − 3 |
= 1, 2 = |
5 + 3 |
= 4. |
2 |
|
|||
|
2 |
|
||
Значит, общее решение запишется в виде
= 1 + 2 4 .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 374.2 |
Назад Вперёд |
Решение задачи 374.2
Составим и решим характеристическое уравнение:
2 − 6 + 9 = 0,
= 36 − 36 = 0,
6= 1 = 2 = 2 = 3.
Значит, общее решение запишется в виде
= 1 3 + 2 3 .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 374.3 |
Назад Вперёд |
Решение задачи 374.3
Составим и решим характеристическое уравнение:
2 + 8 + 25 = 0,
= 64 − 100 = −36,
1,2 = −8 ± 6 = −4 ± 3 . 2
Значит, общее решение запишется в виде
= −4 ( 1 cos 3 + 2 sin 3 ).
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 375.1 |
Назад Вперёд |
Решение задачи 375.1
Выполним подстановку = . Тогда |
|
|
|
|
|
|
|
( 2 − |
). |
||||||||||||||
′ = |
= − , |
′′ = |
2 = |
−2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
||||
Значит исходное уравнение примет вид |
|
|
|
|
− 6 = 0, |
||||||||||||||||||
2 |
−2 |
( 2 − |
) |
+ 2 − |
|
||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
+ |
|
|
|
− 6 = 0. |
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||
Составим и решим характеристическое уравнение: |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
2 + − 6 = 0, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
= 1 + 24 = 25, |
|
|
|
||||||||||||
|
|
1 |
= |
−1 − 5 |
|
= |
− |
3, |
2 |
= |
−1 + 5 |
= 2. |
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||
Значит, общее решение запишется в виде
= 1 −3 + 2 4 .
Возвращаясь к переменной , получим
= 31 + 2 2.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 375.5 |
Назад Вперёд |
Решение задачи 375.5
Выполним подстановку 2 + 1 = , = 12 ( − 1). Тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
′ = |
= |
|
|
|
= 2 − |
, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
′′ = |
|
= |
|
= |
− |
) |
|
= 4 −2 |
|
− |
|
. |
||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
( |
|
) |
||||
|
′ |
|
′ |
|
2 |
|
|
2 − |
|
|
|
|
2 |
|
|
|||||||
Значит исходное уравнение примет вид |
− + 4 = 0, |
|
|
|||||||||||||||||||
|
2 4 −2 |
( 2 − |
|
) − 4 |
|
|
||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
− 2 |
|
+ |
= 0. |
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||
Составим и решим характеристическое уравнение:
2 − 2 + 1 = 0,
= 4 − 4 = 0,
−2
= 1 = 2 = 2 = 1.
Значит, общее решение запишется в виде
= 1 + 2 .
Возвращаясь к переменной , получим
= 1(2 + 1) + 2(2 + 1) ln(2 + 1).
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 376.1 |
Назад Вперёд |
Решение задачи 376.1
Составим и решим характеристическое уравнение:
2 + 4 = 0,2 = −4,
1,2 = ±2 .
Значит, общее решение однородного уравнения запишется в виде
|
|
|
|
|
|
|
|
|
|
0 |
= 1 cos 2 + 2 sin 2 , |
|
|
|
|||||||||||||||||
а фундаментальными решениями будут |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
= cos 2 , |
2 = sin 2 . |
|
|
|
||||||||||||||||
Вычислим определитель Вронского |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
1 |
2 |
|
|
|
− |
|
|
|
|
|
|
|
sin 2 |
|
|
|
|
|
|
|
|
|
|||||||
|
1′ |
|
2′ |
|
|
|
|
|
2 sin 2 |
|
2 cos 2 |
|
|
= 2 cos2 2 + 2 sin2 2 = 2, |
|||||||||||||||||
= |
|
|
= |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и дополнительные |
определители |
( ( ) — правая |
часть исходного уравнения) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
sin 2 |
|
|
|
|
|
|
|
|
|
||||||
1 = |
|
(0 ) |
|
2′ |
= |
|
|
1 |
|
|
2 cos 2 |
|
|
= 0 |
− tg 2 = − tg 2 , |
||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
cos 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
cos 2 |
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
2 |
|
′ |
( ) |
|
= |
|
|
2 sin 2 |
|
|
|
1 |
|
|
|
− 0 = 1. |
|||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
= 1 |
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2 |
|
|
|
||||||||
Определим функции |
|
|
|
|
|
|
|
|
|
∫ |
cos 2 |
|
|
4 ln | cos 2 | + 1, |
|||||||||||||||||
1( ) = ∫ |
|
|
1 = ∫ |
|
− |
|
2 |
|
= −2 |
= |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
tg 2 |
|
|
|
|
1 |
|
|
|
sin 2 |
|
1 |
||||||||
|
|
|
|
|
|
2( ) = ∫ |
2 = |
∫ |
2 |
|
= 2 + 2. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|

Часть II. Задачи |
|
|
|
|
|
|
|
||
Решения и указания |
|
|
|
|
|
|
|
||
Глава 6. Дифференциальные уравнения |
|
|
|
|
|
|
|
||
Меню Решение задачи 376.1 |
|
|
|
|
|
|
Назад Вперёд |
||
|
|
|
|
|
|
|
|
||
Значит, общее решение неоднородного уравнения примет вид |
|||||||||
= 1( ) cos 2 + 2( ) sin 2 = |
( |
2 + 2)sin 2 = |
|||||||
= ( |
4 ln | cos 2 | + 1)cos 2 + |
||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
= 1 cos 2 + 2 sin 2 + |
1 |
sin 2 + |
1 |
cos 2 ln | cos 2 |. |
|||
|
|
|
|
|
|||||
|
|
2 |
4 |
||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 377.1 |
Назад Вперёд |
Решение задачи 377.1
Составим и решим характеристическое уравнение:
2 + 2 + 1 = 0,
= 4 − 4 = 0,
= 1 = 2 = −1.
Значит, общее решение однородного уравнения запишется в виде
0 = 1 − + 2 − .
Правая часть исходного уравнения имеет специальный вид 0( ) , где 0 = 1 — многочлен нулевой степени, а = 1 не является корнем характеристического уравнения. Поэтому частное решение неоднородного уравнения следует искать в виде
( ) = .
Найдем производные
′( ) = , |
′′( ) = . |
Подставим в исходное уравнение вместо и найдем
+ 2 + = , |
4 = 1, |
= |
1 |
. |
|
4 |
|||||
|
|
|
|
Значит, ( ) = 14 , а общее решение неоднородного уравнения запишется в виде
= 0 + = 1 − + 2 − + 14 .
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 377.6 |
Назад Вперёд |
Решение задачи 377.6
Составим и решим характеристическое уравнение:
|
2 + 3 − 4 = 0, |
|
|||||
|
= 9 + 16 = 25, |
|
|||||
= |
−3 − 5 |
= |
− |
4, |
= |
−3 + 5 |
= 1. |
1 |
2 |
|
|
2 |
2 |
|
|
Значит, общее решение однородного уравнения запишется в виде
0 = 1 + 2 −4 .
Правая часть исходного уравнения имеет специальный вид 1( ) , где 1 = + 1 — многочлен первой степени, а = 1 является корнем характеристического уравнения кратноти 1. Поэтому частное решение неоднородного уравнения следует искать в виде
( ) = ( + ) · 1 = ( 2 + ) .
Найдем производные
′( ) = (2 + ) + ( 2 + ) = ( 2 + + 2 + ),
′′( ) = ( 2 + + 2 + ) + (2 + + 2 ) = = ( 2 + 4 + + 2 + 2 ).
Подставим в исходное уравнение вместо
( 2+4 + +2 +2 )+3 ( 2+ +2 + )−4( 2+ ) = ( +1) .

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 377.6 |
Назад Вперёд |
Сократим это уравнение на и приведем подобные слагаемые
10 + 2 + 5 = + 1.
Приравнивая коэффициенты при одинаковых степенях , получим систему
10 = 1,
Откуда = |
1 |
, = |
4 |
|
. |
2 + 5 = 1. |
|
|
|
|
||||
10 |
25 |
|
|
|
|
|||||||||
Значит, ( ) = |
|
1 |
2 + |
4 |
, а общее решение неоднородного урав- |
|||||||||
|
10 |
25 |
||||||||||||
нения запишется в |
виде |
|
|
) |
|
|
|
|
||||||
|
( |
|
|
|
25 ) |
|
||||||||
|
= 0 + = 1 + 2 −4 + (10 2 |
+ |
. |
|||||||||||
|
|
|
|
|
|
|
1 |
|
|
4 |
|
|
||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 377.10 |
Назад Вперёд |
Решение задачи 377.10
Составим и решим характеристическое уравнение:
|
2 − 5 + 6 = 0, |
|
|||||
|
= 25 |
− 24 = |
1, |
|
|||
1 = |
5 − 1 |
= 2, |
2 = |
5 + 1 |
= 3. |
||
2 |
|
2 |
|||||
|
|
|
|
||||
Значит, общее решение однородного уравнения запишется в виде
0 = 1 2 + 2 3 .
Правая часть исходного уравнения имеет специальный вид 0( ) sin , где 0 = 13 — многочлен нулевой степени, а = 3 не является корнем характеристического уравнения. Поэтому частное решение неоднородного уравнения следует искать в виде
( ) = cos 3 + sin 3 .
Найдем производные
′( ) = −3 sin 3 + 3 cos 3 ,′′( ) = −9 cos 3 − 9 sin 3 .
Подставим в исходное уравнение вместо
−9 cos 3 −9 sin 3 −5(−3 sin 3 +3 cos 3 )+6( cos 3 + sin 3 ) = 13 sin 3 .
Приравнивая коэффициенты при cos 3 и sin 3 , получим систему
−9 − 15 + 6 = 0, |
+ 5 = 0, |
|||
− |
9 + 15 + 6 = 13; |
|
− |
3 = 13; |
|
15 |
|
||

Часть II. Задачи Решения и указания
Глава 6. Дифференциальные уравнения
Меню Решение задачи 377.10 |
|
Назад Вперёд |
Откуда = 65 , = −61 .5 |
− |
1 |
Значит, ( ) = 6 cos 3 |
6 sin 3 , а общее решение неоднородного |
|
уравнения запишется в виде |
|
|
= 0 + = 1 2 + 2 3 + 16(5 cos 3 − sin 3 ).
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 378.1 |
Назад Вперёд |
Решение задачи 378.1
Найдем общее решение уравнения. Составим и решим характеристическое уравнение:
|
2 − 4 + 3 = 0, |
|
||
|
= 16 − 12 = 4, |
|
||
1 = |
4 − 2 |
= 1, 2 = |
4 + 2 |
= 3. |
2 |
|
|||
|
2 |
|
||
Значит, общее решение запишется в виде
= 1 + 2 3 .
Чтобы найти частное решение, воспользуемся начальными условиями. Из условия (0) = 6 следует уравнение
6 = 1 + 2.
Чтобы воспользоваться условием ′(0) = 10 найдем производную
|
|
|
′ = 1 + 3 2 3 , |
т.е. |
|
|
|
|
|
|
10 = 1 + 3 2. |
Получим систему |
|
|
1 + 2 = 6, |
|
|
. |
|
1 |
2 |
|
|
|
|
|
1 + 3 2 = 10. |
Откуда = 4, = 2 Значит, частным решением исходного уравнения будет
= 4 + 2 3 .
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 6. Дифференциальные уравнения |
|
Меню Решение задачи 379 |
Назад Вперёд |
Решение задачи 379
Решим указанное уравнение. Соответствующее характеристическое уравнение имеет вид
2 + 2 = 0,
где 2 = ( − ). Учитавая условие задачи > 0. Значит характеристическое уравнение имеет корни 1,2 = ± . Поэтому общее решение однородного уравнения
0 = 1 cos + 2 sin
или после несложных преобразований
0 = cos( − ).
Найдем частное решение неоднородного уравнения. Учитывая вид правой части, его следует искать в виде = . Подставив в исходное уравнение, получим
( − ) = ( − )
откуда
−
= − .
Окончательно, закон изменения цены описыавется функцией
−= 0 + = cos( − ) + − ,
где и — некоторые постоянные. |
[Вернуться к условию] |

Часть II. Задачи Решения и указания Глава 7. Ряды
Меню |
Назад Вперёд |
Глава 7. Ряды

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 380.1 |
Назад Вперёд |
Решение задачи 380.1
Каждый член данного ряда, начиная со второго, представляет собой дробь, числитель которой равен 1, а знаменатель — третья степень числа . Первый
член 1 = |
|
1 |
. Таким образом, = |
1 |
. |
[Вернуться к условию] |
|
3 |
3 |
||||
|
1 |
|
|
|
||

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 381.1 |
Назад Вперёд |
Решение задачи 381.1
Члены этого ряда 1, 12 , 14 , . . . представляют собой геометрическую прогрессию с первым членом 1 = 1 и знаменателем = 12 . Воспользуемся формулой суммы бесконечной геометрической прогрессии:
∞ |
1 |
|
|
1 |
|
|
|
1 |
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
= = 1 |
− |
|
= 1 |
− |
1 |
= 2. |
||||
=0 |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 381.3 |
Назад Вперёд |
Решение задачи 381.3
Общий член этого ряда = |
|
|
1 |
|
|
|
можно представить в виде |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
( +2) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
( + 2) = |
2 |
( |
|
|
− + 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Тогда частичная сумма ряда равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
= =1 = 2 (1 − |
3)+ 2 (2 − 4)+ 2 (3 − 5)+ 2 (4 − 6)+. . . + |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
1 |
|
1 |
|
|
|
|
1 |
|
|
|
1 |
1 |
|
|
1 |
|
1 |
1 |
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
||||||||||||||||||
|
+ 2 |
( − 2 |
− ) + 2 |
|
( − 1 − + 1) + 2 |
( |
− + 2) = |
||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
1 |
|
1 |
1 |
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
= 2 (1 − |
3 + |
2 |
− 4 |
+ 3 |
|
− 5 |
|
+ 4 − |
6 + . . . + |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
1 |
|
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
+ − 2 − + |
− 1 |
− + 1 |
+ − + 2) = |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 (1 + |
2 − |
|
|
+ 1 − |
+ 2). |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ 2 (1 + 2 − + 1 − + 2) = 2 · 2 = 4. |
||||||||||||||||||||||||||||||||||||
=1 ( + 2) = →∞ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
1 |
|
|
|
lim |
|
|
= lim |
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
3 3 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 382.1 |
Назад Вперёд |
Решение задачи 382.1
Так как общий член ряда = 2 1−1 , то получим
|
1 |
|
|
|
lim = |
lim |
|
|
= 0. |
|
||||
→∞ |
→∞ 2 − 1 |
|
||
Значит, необходимое условие сходимости ряда выполняется, о сходимости ряда ничего сказать нельзя. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 382.2 |
Назад Вперёд |
Решение задачи 382.2
Так как общий член ряда = 2 +1+1 , то получим
lim |
= lim |
+ 1 |
= |
1 |
̸= 0. |
|
|
|
|
||||
2 + 1 |
2 |
|||||
→∞ |
→∞ |
|
|
|
|
|
Значит, необходимое условие сходимости ряда не выполняется, ряд расходится. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 383.1 |
Назад Вперёд |
Решение задачи 383.1
1 |
|
1 |
|
|
|
Общий член ряда = √ |
|
= |
|
. Данный ряд является обобщенным гармо- |
|
|
1/2 |
||||
|
|||||
ническим рядом. В силу того, что = 1 |
< 1, ряд расходится. |
||||
|
|
|
|
2 |
|
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 383.2 |
Назад Вперёд |
Решение задачи 383.2
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
Общий член ряда = |
1 |
. Сравним этот ряд с рядом |
∞ |
1 |
. Так как |
||||||||
|
|
|
|
||||||||||
|
|
|
|
·2 |
|
|
|
|
=1 |
2 |
|
||
|
|
|
|
1 |
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
6 |
|
, |
= 1, 2, . . . , |
|
|
|
|
|
∑ |
|
· 2 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
и ряд |
∞ |
1 |
сходится как бесконечная геометрическая прогрессия со знаме- |
||||||||||
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
нателем = 12 < 1, то и исходный ряд сходится по признаку сравнения. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 383.6 |
Назад Вперёд |
Решение задачи 383.6
Общий член ряда |
|
= |
3 2−12 |
−1 |
. Рассмотрим ряд |
∞ 1 при этом = 1 . |
|||||||||||||||
Вычислим предел |
|
|
3 |
+4 |
|
|
|
|
|
|
=1 |
|
|
|
|||||||
|
|
|
|
|
|
|
− 1 |
) |
|
|
∑ |
|
|
|
|||||||
→∞ |
→∞ (3 3 + 4 2 |
→∞ 3 3 + 4 2 − 1 |
3 |
|
|||||||||||||||||
lim |
|
= lim |
|
|
|
2 − |
1 |
|
: |
1 |
|
= lim |
|
3 − |
|
= |
1 |
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∑ |
∞ |
|
1 |
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∞ |
2 |
|
1 |
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Значит, ряды |
|
− 2 |
|
и |
|
|
|
сходятся или расходятся одновременно. В |
|||||||||||||
3 |
−1 |
|
|
|
|||||||||||||||||
=1 |
3 +4 |
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
силу того, что ряд |
|
|
расходится, то и исходный ряд также расходится по |
||||||||||||||||||
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
[Вернуться к условию] |
||||||
|
|
|
в предельной форме. |
|
|
||||||||||||||||
признаку сравнения∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 384.1 |
Назад Вперёд |
Решение задачи 384.1
Общий член ряда = |
+1 |
. Найдем |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 = |
+ 2 |
|
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
( + 1)! |
|
|
|
||||||
Поскольку, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
+1 |
lim |
|
|
+ 2 |
|
|
! |
|
= |
lim |
+ 2 |
= 0 < 1, |
||
|
(( + 1)! · + 1) |
|
|||||||||||||
→∞ |
= →∞ |
|
|
→∞ ( + 1)2 |
|
||||||||||
исходный ряд сходится по признаку Даламбера. |
[Вернуться к условию] |
||||||||||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 385.1 |
Назад Вперёд |
Решение задачи 385.1
Общий член ряда = ( |
2 |
|
) |
|
. Поскольку, |
|
|
|
|||||||
|
|
|
|
|
|||||||||||
3 +5 |
|
lim |
3 2+ 5 = |
3 < 1, |
|||||||||||
lim √ = |
lim |
√ |
|
|
3 + 5 |
|
= |
||||||||
→∞ |
→∞ |
|
|
( |
) |
|
→∞ |
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
исходный ряд сходится по признаку Коши. |
|
[Вернуться к условию] |
|||||||||||||

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 386.1 |
Назад Вперёд |
Решение задачи 386.1
Так как = |
1 |
|
, то ( ) = |
1 |
|
. Очевидно, функция ( ) положительна, |
|||||||||||||||
ln |
|
ln |
|
||||||||||||||||||
непрерывна и монотонно убывает на промежутке (2; +∞). |
|
|
|
|
|
|
|
||||||||||||||
Вычислим несобственный интеграл: |
→+∞ ( |
|
|
|
|
| 2 ) |
|
|
|
||||||||||||
∫ |
∫ |
|
ln |
= →+∞ ∫ |
ln |
|
| |
|
|
|
|
|
|||||||||
+∞ |
+∞ |
1 |
lim |
|
|
(ln ) = |
lim |
ln |
|
ln |
|
|
|
= |
|
|
|||||
( ) = |
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
− |
|
|
|
∞ |
|
|||
|
|
|
|
|
|
|
|
|
|
= |
+ |
|
|
|
ln ln 2) = |
. |
|||||
|
|
|
|
|
|
|
|
|
|
lim (ln ln |
|
|
|
||||||||
→ ∞
Значит, исходный ряд расходится по интегральному признаку.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 387.1 |
Назад Вперёд |
Решение задачи 387.1
Данный ряд является знакопеременным. Исследуем его на абсолютную сходимость. Рассмотрим ряд
|
|
|
|
|
|
∞ |
|
cos |
= |
∞ |
cos |
|. |
||||||
|
|
|
|
|
|
=1 |
|
2 |
|
=1 | |
2 |
|||||||
|
|
|
|
|
|
∑ |
|
|
|
|
|
∑ |
|
|
|
|||
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сравним его с рядом |
1 |
. Так как | cos | 6 1, то и |
||||||||||||||||
=1 |
2 |
|||||||||||||||||
|
|
∑ |
| cos |
| |
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
6 |
, |
= 1, 2, . . . |
|||||||||||
|
|
|
|
|
2 |
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Заметим, что ряд |
∞ |
|
1 |
|
сходится как обобщенный гармонический рад при |
|||||||||||||
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑
= 2. Значит, ряд =1
∑∞ | cos |
2
=1
сходится по признаку сравнения, а исходный ряд сходится абсолютно. [Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 387.2 |
Назад Вперёд |
Решение задачи 387.2
Данный ряд является знакочередующимся. Исследуем его на абсолютную
сходимость. Рассмотрим ряд |
(−1) |
|
|
|
|
|
|
|
|
|
1 . |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
= |
|
∞ |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
∞ 1 |
|
|
|
|
|
|
|
=1 √ + 1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
=1 |
|
√ + 1 |
|
|
|
|||||||||||||||||||||
Сравним его с рядом |
∑ |
|
. Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
(√ + 1 |
: √ ) = →∞ |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
√ |
+ |
1 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
lim |
1 |
|
1 |
|
|
|
|
|
|
lim |
|
|
√ |
|
|
|
= 1, |
|
||||||||||||
|
∞∑ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
а ряд |
√ |
|
|
расходится как обобщенный гармонический рад при = |
2 , то и |
||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ряд |
∑ |
|
|
|
расходится по признаку сравнения, а исходный ряд не является |
||||||||||||||||||||||||||||||
√ |
+1 |
||||||||||||||||||||||||||||||||||
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
абсолютно сходящимся. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Применим признак Лейбница при этом = |
√ |
1 |
. В силу того, что |
|||||||||||||||||||||||||||||||
|
+1 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
lim = lim |
√ |
1 |
|
|
|
= 0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
→∞ |
|
|
→∞ |
|
|
+ 1 |
|
|||||||||||||||||||
и |
|
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
√ |
|
|
> √ |
|
|
|
|
> . . . > √ |
|
|
> |
√ |
|
> . . . , |
|
|||||||||||||||
|
|
|
|
|
2 |
3 |
|
+ 1 |
|
||||||||||||||||||||||||||
данный ряд сходится по признаку Лейбница, причем условно.
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 388.1 |
Назад Вперёд |
Решение задачи 388.1
Зафиксируем и рассмотрим ряд, составленный из абсолютных величин данного ряда, т.е.
∑∞ 1 = ∑∞ 1 .
=1 =1
При каждом фиксированном данный ряд является обобщенным гармоническим рядом, который сходится при всех > 1 и расходится при 6 1. Таким образом, область сходимости данного ряда (1; +∞).
[Вернуться к условию]
Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 388.2 |
Назад Вперёд |
Решение задачи 388.2
Зафиксируем и рассмотрим ряд, составленный из абсолютных величин
данного ряда, т.е. |
2 |
+ 3 |
|
|
∞ |
2 + 3 |
|
∞ |
|
|
|||||
∑ |
|
|
|
∑ |
| | |
|
|
|
|
|
|
|
|
|
|
=1 |
2 +1 |
|
= |
=1 |
2 +1 |
. |
|
Применим признак Даламбера: |
|
|
|
|
|
|
|
|
|
= |
2 |
+ 3 |
|
|
= |
|
( + 1)2 + 3 |
= |
2 |
+ 2 + 4 |
|
|
|
|
|||||||||||
|
|
|
|
|
, |
+1 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||
|
|
| | |
2 +1 |
|
| | |
2( +1)+1 |
|
|
| | |
2 +3 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вычислим предел |
|
|
|
|
|
|
|
| 2| |
+ 3 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
→∞ |
= →∞ ( |
| |2 +3 |
· |
|
→∞ ( 2 |
+ 3)| |2 |
|
|
|
|
|||||||||||||||||
lim |
+1 |
lim |
|
2 |
+ 2 + 4 |
|
|
2 +1 |
= |
lim |
2 |
+ 2 + 4 |
= |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 + 2 + 4 |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
lim |
|
|
|
|
|
= |
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + 3 |
|
| |2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |2 →∞ |
|
|
|
|
|
||||||||
Для того, чтобы этот ряд сходился, достаточно выполнения условия:
1
| |2 < 1,
которое выполняется при (−∞; −1) (1; +∞). Заметим, что при(−1, 1) вычисленный выше предел будет больше 1, т.е. при (−1, 1) исходный ряд расходится.
Осталось выяснить поведение ряда при = ±1. Подмтавим эти значения в данный ряд. Если = 1, то получим ряд
∞ |
2 + 3 |
|
∞ |
∑ |
|
∑ |
|
|
|
= |
( 2 + 3), |
=1 |
12 +1 |
|
=1 |
|
|
||

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 388.2 |
Назад Вперёд |
который расходится по следствию из необходимого условия сходимости числового ряда. Аналогично, если = −1, ряд
∞ |
2 + 3 |
|
∞ |
||
∑ |
|
|
|
= − |
∑ |
|
− |
1)2 +1 |
|||
( |
|
( 2 + 3), |
|||
=1 |
|
|
|
|
=1 |
также расходится. |
|
|
|
|
|
Значит, областью |
|
сходимости исходного ряда является |
|||
(−∞; −1) (1; +∞). |
|
|
|
[Вернуться к условию] |
|

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 389.1 |
Назад Вперёд |
Решение задачи 389.1
Данный ряд является степенным, причем = 1 , 0 = 0. Вначале найдем радиус сходимости по формуле:
Имеем,
Тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
lim |
|
|
|
+1 |
|
. |
|
|
||||
|
|
→∞ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
+1 = |
|
|
|
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
+ 1 |
|
|
|
||||||||
lim |
1 |
+ 1 |
|
= lim + 1 = 1. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= →∞ |
|
|
· |
|
1 |
|
|
|
→∞ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значит, интервал сходимости ( 0 − ; 0 |
+ ) = (−1; 1). |
|||||||||||
Осталось исследовать поведение ряда на концах интервала сходимости. |
||||||||||||
Если = 1, то |
|
|
∞ 1 |
∞ 1 |
||||||||
∞ |
|
|
||||||||||
∑ |
= |
∑ |
= |
∑ |
||||||||
|
|
|
|
=1 |
|
. |
||||||
=1 |
|
|
=1 |
|
|
|
|
|||||
Этот ряд расходится (он является гармоническим рядом). |
||||||||||||
Если = −1, то |
|
= ∞ |
(−1) . |
|||||||||
∞ |
||||||||||||
∑ |
|
|
∑ |
|
|
|
|
|
||||
|
|
|||||||||||
=1 |
=1 |
|
||||||||||
Этот ряд сходится по признаку Лейбница (причем условно). Значит, область сходимости исходного ряда [−1; 1).
[Вернуться к условию]

Часть II. Задачи |
|
Решения и указания |
|
Глава 7. Ряды |
|
Меню Решение задачи 389.6 |
Назад Вперёд |
Решение задачи 389.6
Данный ряд является степенным, причем = ( +1 ) , 0 = 0.
Вначале найдем радиус сходимости по формуле:
|
|
|
|
|
|
= →∞ √| |
| |
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
||||
Получим, |
|
√ |
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
= lim |
( |
|
|
|
|
= |
lim |
|
|
|
= 1. |
|||||||||
1 |
|
→∞ |
|
|
|
) |
|
|
→∞ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Значит, = 1 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
интервал сходимости |
( 0 − ; 0 + ) = (−1; 1). |
|||||||||||||||||||||
Осталось исследовать поведение ряда на концах интервала сходимости. |
||||||||||||||||||||||
Если = 1, то |
=1 ( |
|
|
|
) |
|
|
|
|
|
|
|
( |
|
|
) |
|
|
||||
|
|
|
|
1 |
= |
=1 |
|
. |
||||||||||||||
|
|
|
∞ |
+ 1 |
|
|
|
|
|
∞ |
|
|
|
+ 1 |
|
|
||||||
|
|
|
∑ |
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|||
Этот ряд расходится по следствию из необходимого условия сходимости, т.к.
|
→∞ ( |
|
) |
|
|
|
̸ |
||
|
lim |
+ 1 |
|
|
= = 0. |
||||
Если = −1, то |
∞ |
|
|
|
|
+ 1 |
) |
|
|
|
=1(−1) ( |
|
. |
||||||
|
∑ |
|
|
|
|
|
|
|
|
Этот ряд также расходится (аналогично).
Значит, область сходимости исходного ряда (−1; 1).
[Вернуться к условию]
