где m и b вычисляются из уравнения (5.14 ), а n является числом значений функции Q(x), которые используются при подгонке. Для хороших подгонок χ2/ν должно быть близко к 1,00 (см. [5], где в доступной форме представлены описания свойств χ2/ν). Величина χ2/ν действительно составляет ~ 1,00 для пиков, которые имеют хорошую форму. Так как максимальное число отсчетов в канале увеличи- вается, то χ2/ν возрастает, даже если форма пика остается такой же. Возрастание χ2/ν не обязательно означает, что подгонка не отвечает требованиям определения градуировочной энергии или проверке разрешения. При низкой точности высокому качеству подгонки препятствует недостаточная статистика отсчетов; а при высокой точности ему мешают неизбежные небольшие отклонениями формы пика от истинной формы кривой Гаусса, которые приводят к увеличению вычисляемого значения χ2/ν. Практика подскажет приемлемое значение χ2/ν для данного диапазона точности пика.

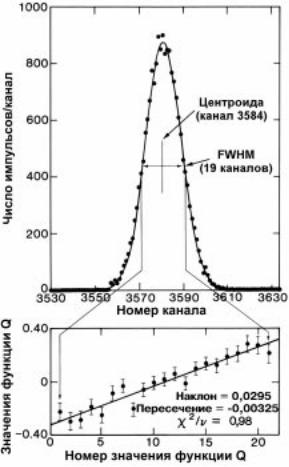
На рис. 5.6 показан пик спектра, измеренного с низкой точностью при помощи германиевого детектора (FWHM ~ 19 каналов), вместе с наложенной на него подгоняемой функцией Гаусса. Нижняя часть рисунка показывает график функции Q(x) от x для верхних двух третей пика вместе с подгоняемой линией, а также параметры рассматриваемого пика.

5.1.9Определение положения пика с использованием подгонки параболаризованной функцией Гаусса

Натуральный логарифм функции Гаусса является параболой, что становится заметным, когда пики полного поглощения рассматриваются с использованием дисплея МКА в логарифмическом масштабе. Натуральный логарифм функции Гаусса (уравнение (5.6)) представляется в виде

ãäå c2 = −1 / 2σ2 ; c1 = x0 / σ2 ;

c0 = ln y0 − x20 / 2σ2 .

Подгонка уравнения (5.20) к набору точек (xi, ln yi) дает значения c2, c1 è c0, которые позволяют получить параметры кривой Гаусса:

x0 = −c1 / 2c2 ;

Подгоняемая кривая является параболой, которая направлена крыльями вниз, а ее ось параллельна оси y. Процедура, описанная здесь, позволяет определить значение y0 в дополнение к двум параметрам: x0 и b, полученным с помощью подгонки линеаризованной функцией Гаусса. Следовательно, площадь пика полного поглощения можно определить с помощью уравнения (5.8).

На рис. 5.7 показана подгонка параболаризованной кривой Гаусса к пику спектра высокой точности от гамма-излучения 57Co с энергией 122,0 кэВ. Использовался тот же германиевый детектор высокого качества, что и на рис. 5.3(а). Сбор

Ðèñ. 5.6. Верхняя часть рисунка показывает пик, измеренный с низкой точностью при помощи детектора высокого разрешения, к которому подгоняла сь линеаризованная функция Гаусса. Нижняя часть рисунка показывает график то чечных значений Q(x) и подогнанную линию

заряда на низких энергиях в германиевом детекторе производился более полный, чем на высокий энергиях, что привело к меньшему затягиванию низкоэнергети- ческого хвоста. Сравнение рис. 5.3 (а) и 5.7 показывает, что затягивание хвоста пика 122 кэВ на рис. 5.7 даже ниже, чем небольшое затягивание хвоста пика 1332 кэВ на рис. 5.3 (а).

Ðèñ. 5.7. Участок спектра с пиком полного поглощения 57Сo с энергией 122,0 кэВ. Спектр получен с помощью коаксиального германиевого детектора вы сокого разрешения с хорошей формой пика полного поглощения. Кривой подгонки я вляется параболаризованная функция Гаусса

Выражения для подгонки взвешенных наименьших квадратов приведены здесь для удобства возможных пользователей. Выражения даны в форме определителей и включают восемь сумм, обозначенных S1, S2, ..., S8.

Как обычно, суммирование производится по всем точкам подгонки. В значе- ниях yi вычтен фон. Кроме того, для процедуры подгонки требуются следующие выражения:

si = s(ln yi ),

где s(y) определяется уравнением (5.17). Выражение для χ2/ν, которое представляет статистику качества подгонки, определяется следующ ей формулой:

где n — число точек подгонки, а c2, c1 è c0 — величины, которые определяются из уравнения (5.22).

Замечания, сделанные в предыдущем разделе относительно части пика, которую следует подгонять, и относительно тенденций статистики χ2/ν в данном слу- чае также справедливы. Квадратичные подгонки предъявляют определенные требования к компьютеру, и для выполнения правильной квадратичной подгонки с заданной точностью часто недостаточно шестизначных десятичных цифр, которые обеспечиваются 16-ти разрядными процессорами, работающими с одинарной точностью.

5.1.10 Определение положения пика с помощью сложных программ подгонки спектра

Для анализа сложных спектров с перекрывающимися пиками используются большие вычислительные программы подгонки. Они описывают пики функциями, которые используют функцию Гаусса в качестве основной, с добавлением хвостовых функций для более точного описания формы пика. Для подгонки данных используется итерационная нелинейная процедура наименьших квадратов. Центроида функции Гаусса, которая является составляющей пика, принимается за положение пика и используется для определения значения энергии рассматриваемого гамма-излучения.